含磁滯補償的電液伺服系統預設性能跟蹤控制

董振樂　馬大為　姚建勇　王曉鋒

南京理工大學，南京，210094

?

含磁滯補償的電液伺服系統預設性能跟蹤控制

董振樂馬大為姚建勇王曉鋒

南京理工大學，南京，210094

針對電液伺服系統普遍存在的參數不確定性、不確定非線性(磁滯、摩擦、外干擾等)，提出一種基于自適應魯棒控制的含磁滯補償的預設性能跟蹤控制策略。以閥控單出桿液壓缸位置伺服系統為例，首先建立了含磁滯非線性的系統數學模型，然后通過定義預設性能函數，實現了對跟蹤誤差收斂速率、最大超調量和穩態精度的預先規劃，基于規劃后的轉換誤差設計了自適應魯棒控制器，并提高了穩態和瞬態跟蹤性能。仿真對比結果表明：該控制策略可以減小磁滯對系統跟蹤精度的影響，提高跟蹤誤差的收斂速度，減小最大超調量，最終實現優良的跟蹤性能。

電液伺服系統；磁滯；預設性能控制；建模不確定性；自適應魯棒控制

0　引言

電液伺服系統具有功率密度大、響應快、輸出力/力矩大等突出優點，在工業和國防領域得到了廣泛的應用[1-2]。然而電液伺服系統存在的參數不確定性(如伺服閥的流量增益、液壓油的體積模量、液壓缸的泄漏系數等)和不確定非線性(如未建模外干擾、非線性摩擦、磁滯等)給控制器的設計帶來了很大難度。

自適應控制是針對參數不確定的常用技術手段[3]，可以有效地估計系統未知參數和可參數化的系統不確定非線性并實現較好的模型補償，但對不可參數化的不確定非線性無能為力。針對不確定非線性，可采用滑模控制[4]、魯棒控制[5]、神經網絡控制[6]等方法處理。

以上控制方法，常常只關注系統的穩態跟蹤性能，對于跟蹤誤差超調量、收斂速度等瞬態指標，卻很少涉及。實際系統運行時，一旦出現超調量過大、收斂過慢等不理想狀況，系統性能必然受損，嚴重時甚至造成執行器失效。針對此類問題，Rovithakis等[7]提出了預設性能控制，即通過定義預設性能函數，對系統跟蹤誤差的超調量、收斂速度等瞬態性能指標以及跟蹤精度等穩態指標施加約束，通過誤差轉換，將原始受限的跟蹤誤差轉換為新的設計誤差，并基于此進行了控制器的設計，保證了系統的穩態性能和瞬態性能。需要說明的是，文獻[7]中預設性能函數的定義是獨立于控制器設計的，這極大地方便了預設性能控制與其他高性能控制器的結合，從而在許多系統中得到了較好的應用[8]。

此外，某些液壓元器件(電液伺服閥中的力矩馬達、壓電直驅伺服閥中的壓電材料等)普遍存在磁滯特性，它極易導致系統在低頻時的相位滯后[9]，影響控制器的最終性能。針對此類問題，文獻[10]將磁滯特性建模為線性項和有界干擾項的組合，該模型簡單，給磁滯補償控制器的設計提供了便利，也在許多領域得到了應用[11]。文獻[12]提出一種基于磁滯逆模型的磁滯補償方法，然而相比于文獻[10]所述方法，該方法稍顯復雜。

本文以某閥控單出桿液壓缸位置伺服系統為例，首先建立了包含磁滯非線性[11]的系統數學模型，在模型中同時考慮系統參數不確定性和不確定非線性。然后在自適應魯棒控制的基礎上，融合預設性能控制，不但獲得了較好的穩態跟蹤性能，而且保證了預先設定的瞬態性能指標。最后通過仿真驗證了控制器的有效性。

1　含磁滯非線性的系統建模

1.1磁滯模型

由于傳統間隙類磁滯模型的不連續特性對非線性系統的控制器設計十分不利，故本文根據文獻[10]，給出如下磁滯模型：

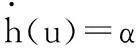
(1)

式中，u、h(u)分別為磁滯模型的輸入(控制輸入)和輸出；α、c、B1為磁滯參數，均為常數，c>B1。

式(1)所描述磁滯特性曲線如圖1所示，磁滯模型參數c=1.3，B1=0.9，α=10。

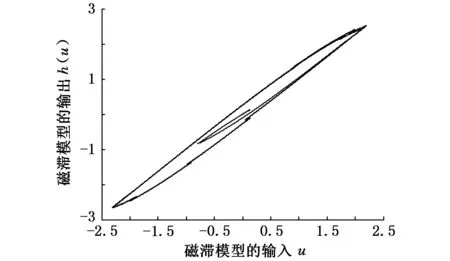
圖1　磁滯特性曲線

求解式(1)可得[10]

h(u)=cu(t)+dh(u)

(2)

式中，h(u0)、u0分別為h(u)和u的初值。

分析式(2)易知，轉換后的磁滯模型由斜率為c的線性項和非線性干擾項dh(u)組成。對于dh(u)項，由文獻[10]可得如下結論：

進一步分析式(2)易知，干擾項dh(u)指數收斂至相應界值。在下一步液壓系統的建模中，式(2)中的磁滯模型將會考慮在內，同時將基于該磁滯模型進行磁滯特性補償。

1.2液壓系統非線性數學模型

本文中的單出桿液壓缸位置伺服系統原理如圖2所示，伺服閥控制液壓缸直接驅動慣性負載做直線運動。根據牛頓第二定律，慣性負載動力學方程為

(3)

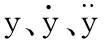
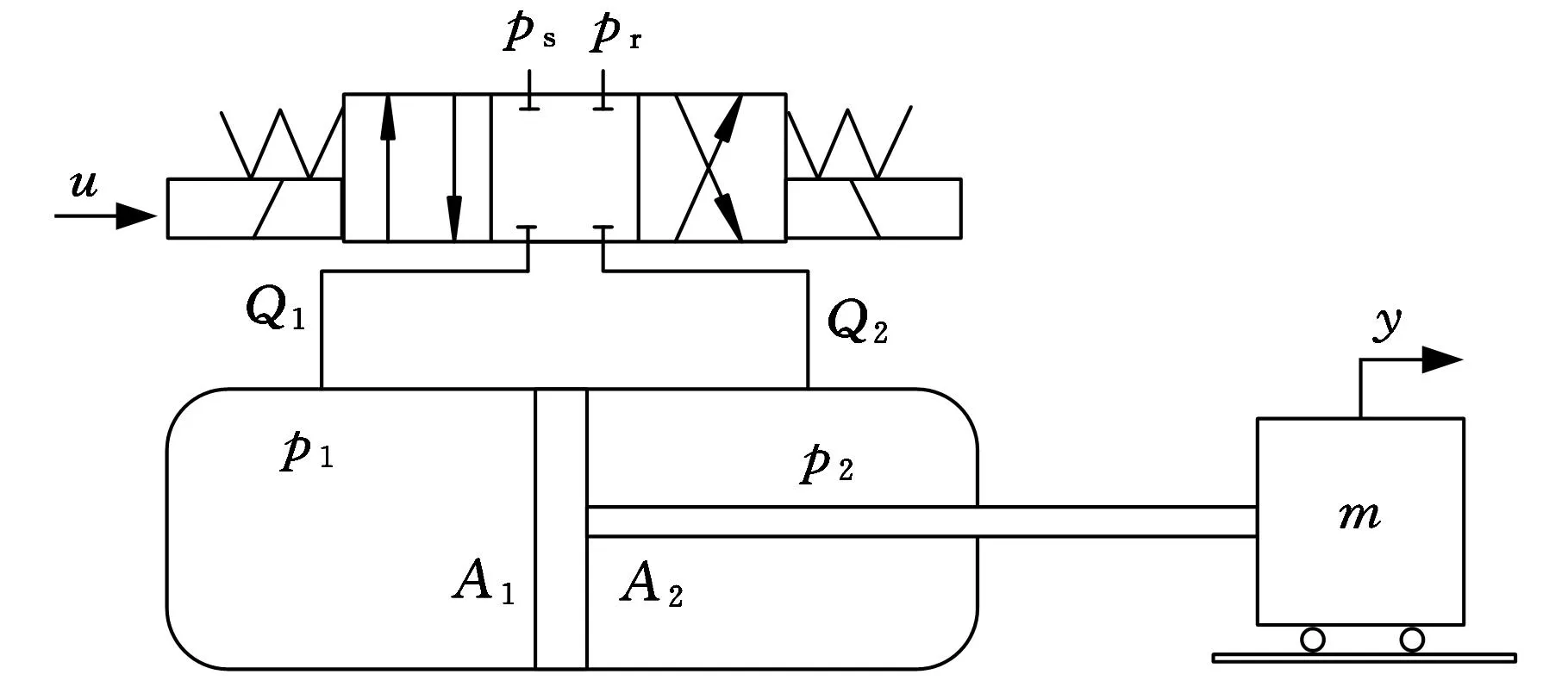
圖2　閥控單出桿液壓缸位置伺服系統原理示意圖

執行器兩腔壓力的動態方程為[9]

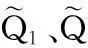
由文獻[9]可知，負載流量QL和伺服閥閥芯位移xv的關系為

(5)

式中，Cd為伺服閥節流孔系數；w為伺服閥節流孔面積梯度；ρ為液壓油密度；ps為系統供油壓力；pr為系統回油壓力，pr=0。

由于伺服閥的頻寬遠大于系統工作時的頻寬，因此建模時我們忽略伺服閥的動態過程[13]，將閥的控制輸入和閥芯位移視為比例環節，即xv=kih(u)，其中，ki為電壓-閥芯位移的增益系數，則式(5)轉化為

(6)

定義狀態變量

同時結合式(3)～式(6)，并代入式(2)可得系統總數學模型：

(7)

θ1=B/mθ2=Af/mθ3=ckvK/m

g=A1R1/V1+A2R2/V2

f2=(A1/V1+A2/V2)pL

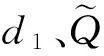
2　預設性能控制器設計

2.1預設性能函數

定義跟蹤誤差e=x1-x1d，假設其需滿足以下性能指標：

-δlρ(t)0

(8)

其中，δu、δl為正的設計參數，用于輔助約束跟蹤誤差的上下限；ρ(t)為正的遞增光滑函數[8]：

ρ(t)=(ρ0-ρ∞)e-kt+ρ∞

其中，ρ0、ρ∞和k均為正的可設計參數；-δlρ0、δuρ0分別約束了誤差的最大下沖量和最大超調量。參數k可調節跟蹤誤差的收斂速度，ρ∞可調節跟蹤誤差的穩態界。顯然，式(8)對跟蹤誤差的性能給出了具體的規劃。為了便于后續控制器的設計，定義如下遞增函數[9]：

(9)

分析易知，式(9)等價于e(t)=ρ(t)S(z1(t))，且z1(t)有界時，預設性能式(8)始終滿足。

選取的遞增函數S(z1)：

(10)

求取式(10)的反函數，可得

(11)

接下來針對轉換誤差z1進行控制器設計。

2.2控制器設計

對式(11)求導可得

(12)

進一步可得

(13)

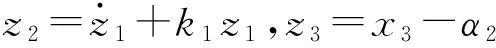
β(z3+α2-θ1x2-θ2Sf+d1)

(14)

設計虛擬控制量α2為

(15)

將式(15)代入式(14)，可得

(16)

φ1=β[x2Sf000]T

若設計α2s2滿足如下鎮定條件[3]：

(17)

式中，ε1為任意小的可設計參數，ε1>0。

則滿足式(17)的α2s2設計如下：

(18)

式中，θM為參數的最大攝動量矩陣，θM=θmax-θmin；θmax、θmin分別表示各參數的估計上界矩陣和估計下界矩陣。

進一步有

(19)

(20)

進一步，最終控制器可設計為

(21)

us1=-k3z3

式中，k3為待設計的反饋增益，k3>0；ua為基于模型的補償項；us1、us2為魯棒項。

將式(21)代入式(19)，可得

(22)

若設計us2滿足下式[3]：

(23)

式中，ε2為任意小的可設計參數，ε2>0。

則滿足式(23)的us2為

(24)

h2≥‖θM‖‖φ2‖+|?α2/?x2|δ1+δ2

選取參數自適應律：

(25)

式中，Γ為可設計自適應增益矩陣，Γ=diag(Γ1，Γ2，…，Γ5)。

控制系統總體結構如圖3所示。

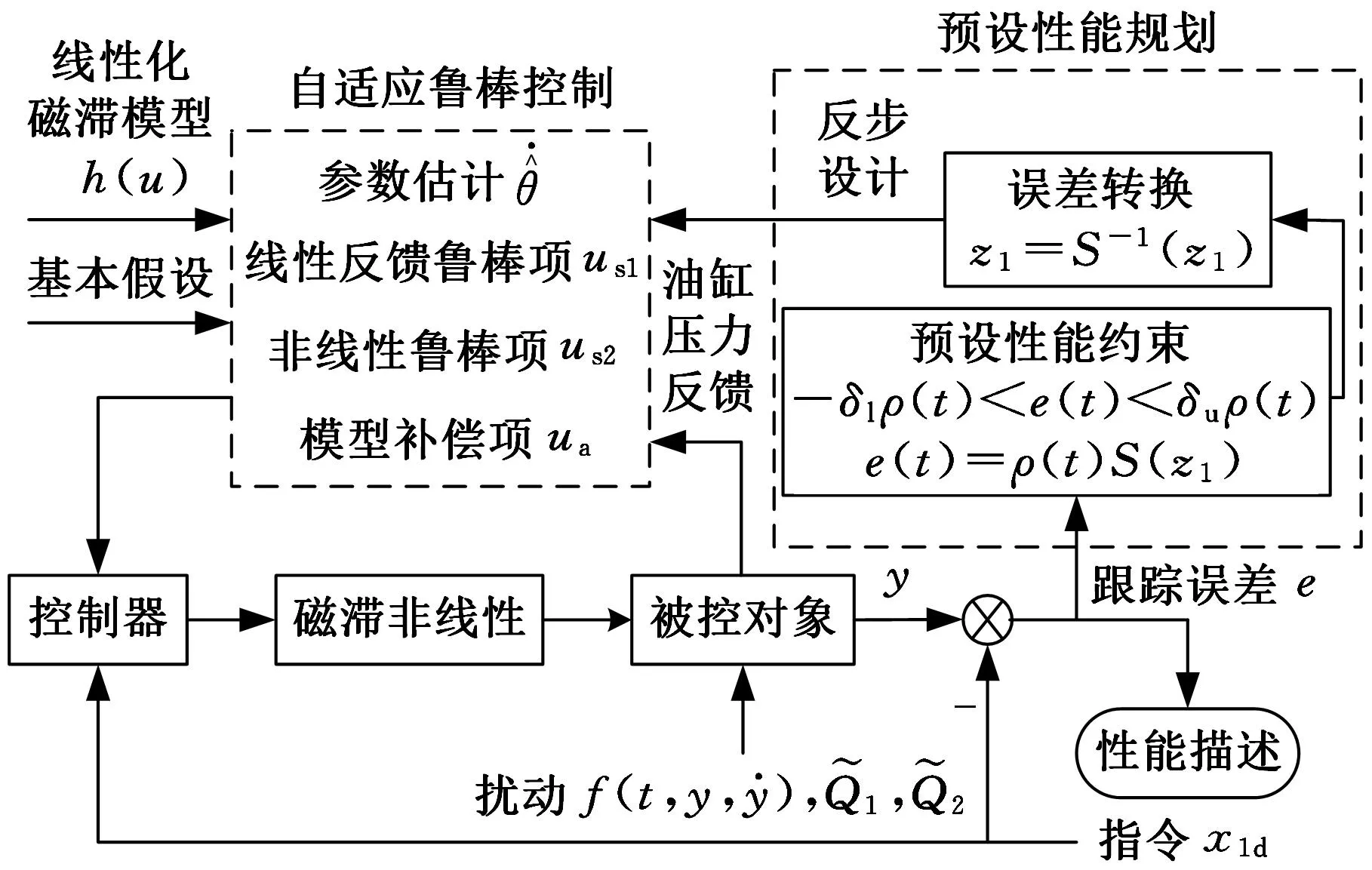
圖3　控制系統總體框圖

2.3穩定性證明

選取系統初始條件滿足-δlρ(0)

選取Lyapunov函數：

(26)

對式(26)求導，并結合式(16)、式(22)，可得

(27)

Z=[z1z2]Tε=ε1+ε2

通過合理地選取參數k1、k2和k3，使得矩陣Λ為正定矩陣，若定義λmin(Λ)為矩陣Λ的最小特征值，則由式(27)可得：

(28)

由式(28)可知，通過合理地選取參數k1、k2和k3，控制器(式(21))可實現系統有界穩定，即轉換跟蹤誤差z1有界；進一步由式(9)、式(10)可知，所設計控制器可保證跟蹤誤差e1有界，進一步通過調節ρ0、ρ∞、k、δl和δu等參數，可使得系統最終滿足式(8)中所描述的預設性能。

3　仿真與分析

本文所研究閥控液壓缸系統具體參數如表1所示。為了充分驗證本文所設計控制器的有效性，在MATLAB/Simulink中搭建系統仿真模型，選取以下3個控制器進行對比仿真驗證。

(1)自適應魯棒控制(adaptiverobustcontrol，ARC)。該控制器使用廣泛，其具體形式可參考文獻[1]，參數k1=100，k2=150，k3=300。

(2)含磁滯補償的預設性能自適應魯棒控制(prescribedperformanceadaptiverobustcontrolwithhysteresiscompensation，PPARCH)，即為本文所設計控制方法，控制器各參數如下：k1=100，k2=50，k3=150，ρ0=0.3，ρ∞=0.001，k=0.5，δl=δu=10。自適應律(式(25))中的參數Γ=diag(40，2.5，0.02，1×1014，1×10-7)。

(3)不含磁滯補償的預設性能自適應魯棒控制(prescribed performance adaptive robust control，PPARC)，即在控制器設計過程中，忽略磁滯特性的模型補償，而仿真時在系統模型中加入磁滯環節。各控制器參數選取同PPARCH。

表1　閥控單出桿液壓缸位置伺服系統參數

系統參數估計的上下界矩陣分別為

θmin=[000.012×1060]T

θmax=[510.58×1060.0001]T

參數估計初值矩陣為

θ0=[000.012×1060.0001]T

系統外干擾d=0.5sin(2πt)，系統初始位置x1(0)=0.1 m，顯然該初始位置滿足初始條件要求-δlρ(0)

選取系統位置跟蹤指令x1d=(1-exp(-0.01t2))arctan(sint)，如圖4所示。

圖4　位置跟蹤指令

磁滯模型曲線見圖1，系統仿真曲線如圖5～圖8所示。

圖5　PPARCH作用下的控制輸入

圖6　初始段0～0.3 s跟蹤誤差對比

圖7　穩態段20～50 s跟蹤誤差對比

圖8　PPARCH參數估計

圖5所示為PPARCH下的控制輸入曲線，顯然，受磁滯非線性的影響，控制輸入在峰值處存在輕微的抖動，但控制輸入整體光滑且始終有界。圖6所示為初始段0～0.3s的跟蹤誤差。由于初始位置不匹配，因此在跟蹤初始時刻，3個控制器的系統跟蹤誤差均較大，但都以較快速度收斂，其中，ARC出現了較大的超調，PPARC和PPARCH在預設性能函數的作用下，無明顯超調，且跟蹤誤差收斂速度快于ARC。圖7所示為穩態段(20～50s)的跟蹤誤差，ARC的跟蹤誤差較大，約為0.03mm，PPARC(約0.02mm)較ARC有了較大改善，PPARCH通過對磁滯的補償作用，跟蹤誤差進一步減小，實現了最佳的跟蹤精度(約0.01mm)。圖8給出了系統各參數的估計曲線，由于初始位置不匹配，初始段各參數估計值出現了較大的突變，然而在自適應律的作用下，各曲線逐漸收斂并保持穩定。

4　結論

(1)將系統磁滯非線性模型簡化為線性項和有界干擾項之和，可便于后續控制器的設計。

(2)通過設計預設性能函數，對系統跟蹤誤差的超調量、收斂速度、穩態精度等性能指標進行了合理了規劃，并結合自適應魯棒控制策略，設計了優良的預設性能控制器。

(3)通過與傳統自適應魯棒控制器的仿真對比，驗證了預設性能函數對跟蹤誤差瞬態性能的改進作用；通過與不含磁滯補償的預設性能控制器進行仿真對比，驗證了所使用磁滯補償策略的有效性。

[1]趙靜一，程斐，郭銳，等. 自行式載重車懸架升降電液同步驅動控制研究[J]. 中國機械工程，2014，25(7)：972-978.

ZhaoJingyi,ChengFei,GuoRui,etal.ResearchonElectro-hydraulicSynchronizationDrivingControlforSelf-propelledTransporterSuspensionLifting[J].ChinaMechanicalEngineering, 2014, 25(7):972-978.

[2]YaoJianyong,JiaoZongxia,ShangYaoxing,etal.AdaptiveNonlinearOptimalCompensationControlforElectro-hydraulicLoadSimulator[J].ChineseJournalofAeronautics, 2010, 23(6): 720-733.

[3]YaoBin,BuFanping,ReedyJ,etal.AdaptiveRobustMotionControlofSingle-rodHydraulicActuators:TheoryandExperiments[J].IEEE/ASMETransactionsonMechatronics, 2000, 5(1): 79-91.

[4]唐銳，王少江，侯力，等. 并聯機床伺服系統雙自適應模糊滑膜控制[J]. 農業機械學報，2012，43(10)：229-234.

TangRui,WangShaojiang,HouLi,etal.DoubleAdaptiveFuzzySlidingModeControlforValveControlledAsymmetricCylinderSystem[J].TransactionsoftheChineseSocietyforAgriculturalMachinery, 2012, 43(10):229-234.[5]ZhaoJiangbo,WangJunzheng,WangShoukun.FractionalOrderControltotheElectro-hydraulicSysteminInsulatorFatigueTestDevice[J].Mechatronics, 2013, 23(7): 828-839.[6]徐勝男，周祖德，艾青松，等. 基于粒子群優化的神經網絡自適應控制算法[J]. 中國機械工程，2012，23(22)：2732-2738.

XuShengnan,ZhouZude,AiQingsong,etal.NeuralNetworkAdaptiveControlAlgorithmModifiedbyPSO[J].ChinaMechanicalEngineering, 2012, 23(22):2732-2738.

[7]RovithakisGA,BechlioulisCP.RobustAdaptiveControlofFeedbackLinearizableMIMONonlinearSystemswithPrescribedPerformance[J].IEEETransactiononAutomaticControl, 2008, 53(9): 2090-2099.

[8]BechlioulisCP,RovithakisGA.PrescribedPerformanceAdaptiveControlforMulti-inputMulti-outputAffineintheControlNonlinearSystems[J].IEEETransactiononAutomaticControl,2010, 55(5): 1120-1226.

[9]MerrittHE.HydraulicControlSystems[M].NewYork:Wiley, 1967.

[10]SuCY,StepanenkoY,SvovodaJ,etal.RobustAdaptiveControlofaClassofNonlinearSystemswithUnknownBacklash-likeHysteresis[J].IEEETransactiononAutomaticControl, 2000, 45(2): 2427-2432.

[11]ZhouJing,WenChangyun,ZhangYing.AdaptiveBacksteppingControlofaClassofUncertainNonlinearSystemswithUnknownBacklash-likeHysteresis[J].IEEETransactiononAutomaticControl, 2004, 49(10): 1751-1757.

[12]RudermanM,BertramT.ControlofMagneticShapeMemoryActuatorsUsingObserver-basedInverseHysteresisApproach[J].IEEETransactiononControlSystemsTechnology, 2014, 22(3): 1181-1189.

[13]YaoJianyong,JiaoZongxia,MaDawei.Extended-state-observer-basedOutputFeedbackNonlinearRobustControlofHydraulicSystemswithBackstepping[J].IEEETransactionsonIndustrialElectronics, 2014, 61(11): 6285-6293.

(編輯張洋)

Prescribed Performance Tracking Control of Electro-hydraulic Servo Systems with Hysteresis Compensation

Dong ZhenleMa DaweiYao JianyongWang Xiaofeng

Nanjing University of Science and Technology，Nanjing，210094

For the common parametric uncertainties and uncertain nonlinearities(hysteresis, nonlinear friction, external disturbances, et al) existing in electro-hydraulic servo systems, a novel method was proposed, which was based on adaptive robust control, and named prescribed performance tracking control with hysteresis compensation. First, taking valve controller single-rod hydraulic cylinder position servo system for instance, a mathematic model consisting of hysteresis nonlinearity was constructed. And then, a prescribed performance function was utilized to characterize the convergence rate, maximum over-shoot, and steady-state errors. At last, an adaptive robust controller was design based on the planned tracking errors to guarantee the excellent steady-state performance and transient performance. Extensive simulations show that the proposed controller can attenuate the hysteresis effects on the tracking accuracy, improve the convergence rate, reduce the over-shoot, and eventually achieve an excellent tracking.

electro-hydraulic servo system; hysteresis; prescribed performance control; modeling uncertainty; adaptive robust control

董振樂，男，1988年生。南京理工大學機械工程學院博士研究生。主要研究方向為機電液伺服系統非線性控制。發表論文3篇。馬大為，男，1953年生。南京理工大學機械工程學院教授、博士研究生導師。姚建勇，男，1984年生。南京理工大學機械工程學院副研究員。王曉鋒，男，1962年生。南京理工大學機械工程學院研究員、博士研究生導師。

2015-04-07

國家自然科學基金資助項目(51305203)；江蘇省自然科學基金資助項目(BK20141402)

TP271.3

10.3969/j.issn.1004-132X.2016.08.001