氣缸沖擊動力學建模與仿真分析

杜群貴　孫智權　黃崇溪　翟曉晨

華南理工大學,廣州,510640

?

氣缸沖擊動力學建模與仿真分析

杜群貴孫智權黃崇溪翟曉晨

華南理工大學,廣州,510640

將氣缸在行程末端的沖擊問題看成一個由細長活塞桿、質量負載、活塞以及端蓋組成的振動系統。首先應用彈性體的一維波動方程建立細長活塞桿縱向振動變形的數學模型，用模態疊加方法解析了沖擊力、接觸位移以及接觸時間。然后利用非線性有限元軟件LS-DYNA對氣缸沖擊過程進行數值仿真計算分析，詳細研究了當驅動負載質量以及活塞初始沖擊速度不同時，活塞沖擊接觸面接觸合力和接觸作用時間的變化情況。對比分析了理論解析解與LS-DYNA數值解，驗證了解析解的準確性，得出了沖擊力分別隨速度和負載的變化規律；進一步對沖擊振動響應進行了頻率分析，并研究了氣缸沖擊力的變化原因。研究結果為氣缸的設計和使用提供了理論和實際參考。

氣缸沖擊力；解析解；LS-DYNA仿真；頻率分析

0　引言

隨著氣動技術的飛速發展，氣缸廣泛地應用于各種工業生產線上。但是，由于氣動系統中介質空氣的高度可壓縮性和低黏度等內在固有特性，當活塞運行到行程末端時就會產生沖擊端蓋現象。同時，氣缸也不可避免地會由于安裝制造誤差、供氣壓力波動、緩沖不良、負載慣性以及運行一段時間之后緊固螺栓松動等外在因素，產生活塞沖擊端蓋現象[1]，并伴隨著不良振動與噪聲，這也是導致氣缸失效的最主要原因。

氣缸的沖擊問題是一個經典的桿結構彈性碰撞力學問題。近年來，國內外學者針對桿的彈性碰撞問題作了很多研究。文獻[2]采用波傳播法給出了質點和均勻桿縱向碰撞響應解析解；文獻[3-4]也采用波傳播法解析了一般邊界條件下桿的縱向沖擊振動問題 ，但解析式隨著波傳播次數的增加而變得過于復雜，其工程應用難以推廣。文獻[5-6]采用模態分析方法解析了桿的點彈性碰撞問題，但局限于特殊的邊界條件；文獻[7-8]采用直接模態疊加法將碰撞問題轉化為具有初速度的振動問題，解析了不同邊界條件、多種截面形狀的桿類沖擊問題的頻率方程及動力響應。但是，對于類似氣缸存在復雜邊界和初始條件下的沖擊破壞現象的建模研究甚少，對其沖擊力大小的預估大都基于經驗。

基于以上原因，本文在不考慮緩沖墊和氣緩沖的情況下對氣缸沖擊現象進行簡化建模研究，求解出沖擊力的解析式，并與有限元仿真數值解進行了對比，從而驗證解析式的可靠性，此外，還分析了沖擊力波動變化的規律及原因。

1　氣缸碰撞系統建模與解析

本文所研究的標準型單桿雙作用氣缸結構簡圖如圖1所示。

1.質量負載　2.活塞桿　3.端蓋　4.活塞　5.缸筒圖 1　氣缸結構簡圖

該氣缸缸筒與無桿側端蓋壓成一體，缸筒與有桿端蓋3處的連接為螺紋連接，軸向尺寸短，質量比其他系列氣缸小10%～15%。氣缸最大工作壓力為1.0 MPa,活塞工作速度為50～1000 mm/s，主要運用于裝配生產線上輕型物料輸送。

筆者在該氣缸可靠性試驗研究的過程中發現氣缸工作一段時間之后，會出現端蓋與缸筒螺紋連接松脫失效以及氣缸安裝緊固螺栓松動的現象。這是由于行程末端活塞對端蓋的長期沖擊造成的，故對此沖擊現象進行建模研究。

對氣缸碰撞系統數學建模時，為了便于簡化分析，將質量負載看成細長活塞桿左端部的一個集中質量，將活塞看成活塞桿右端部的一個集中質量，集中質量隨桿端橫截面一起振動。將端蓋與活塞的碰撞接觸部分看成一個等效接觸彈簧，活塞、活塞桿和負載以一定的初速度沖擊接觸彈簧，彈簧壓力等效為氣缸沖擊力[9]。并認為沖擊過程中桿的橫截面始終保持為平面，且界面上的應力分布均勻，忽略各部分重力的影響。其碰撞系統簡化模型如圖2所示。

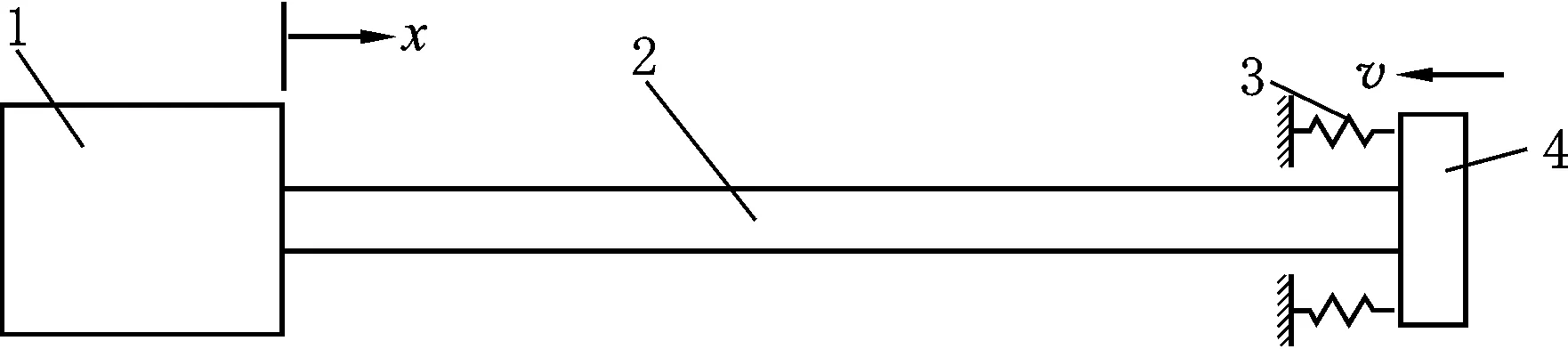
1.質量負載　2.活塞桿　3.等效接觸彈簧　4.活塞圖 2　碰撞系統簡化模型

1.1碰撞系統數學模型的建立

圖2中活塞桿長為l，橫截面積為A，質量密度為ρ，彈性模量為E，等效接觸彈簧剛度系數為k，負載質量為M，活塞質量為m，將質量負載位置處桿端作為坐標原點，分別建立桿的縱向碰撞問題的控制方程、邊界條件和初始條件[10]。

桿的自由振動方程:

(1)

式中，u為桿的縱向振動位移；x為桿的某一橫截面距離坐標原點的位移；t為振動時間。

碰撞過程中邊界條件:

(2)

(3)

初始條件:

u(x,0)=0

(4)

(5)

(6)

邊界條件轉化為

(7)

(8)

初始條件轉化為

(9)

(10)

1.2碰撞模型的求解

(11)

(12)

(13)

(14)

其中，λ為無因次頻率，由式(11)得到主振型通解為

U(ξ)=acosλξ+bsinλξ

(15)

式中，a、b分別為主振型中余弦、正弦信號的幅值。

將式(15)代入式(13)、式(14)得

(16)

由式(16)得到頻率方程：

(17)

由式(15)、式(17)得到各階主振型函數：

(18)

由式(12)解得各階時間函數：

Ti(τ)=Cicosλiτ+Disinλiτ

(19)

式中，Ci、Di分別為第i階時間函數中余弦信號和正弦信號的幅值。

根據模態疊加法，桿的振動位移為無窮個主振動的疊加：

(20)

1.3主振型的正交性求解

為了求得各階時間函數中系數Ci、Di，首先應求得主振型之間的正交性。設Ui(ξ)、Uj(ξ)分別是對應于無因次頻率λi及λj的主振型，由式(11)有

(21)

(22)

對式(21)等號兩邊同時乘以Uj(ξ)并對其從0到1求積分，得

(23)

利用分部積分法可將式(23)等號左邊寫為

(24)

聯立式(23)、式(24)并化簡，得

(25)

同理，對式(23)化簡得

(26)

(27)

為了便于連續性求解，引入δ函數，得到主振型的正交性關系式：

(28)

(29)

1.4沖擊接觸求解

由初始條件可得

(30)

(31)

利用主振型的正交性，將式(30)、式(31)等號兩邊同時乘以[α+δ(ξ)+αηδ(ξ-1)]Ui(ξ)，然后從0到1區間求定積分，可以求解得到:

Ci=0

(32)

(33)

則桿的振動位移解析式為

(34)

在活塞沖擊端蓋處，有x=l，將其代入式(34)，可得到沖擊處桿端橫截面振動位移：

(35)

用等效接觸彈簧所受的壓力大小來表征碰撞過程中沖擊力大小，得到沖擊力表達式：

(36)

2　基于LS-DYNA的有限元仿真分析

以圖1所示的典型氣缸結構為基礎，忽略結構中倒角、圓角、氣孔等因素，根據該氣缸實際結構尺寸，建立簡化的有限元仿真模型。由于氣缸為軸對稱性結構，利用其對稱性可以簡化模擬過程和減少自由度，并縮短分析所需計算時間。本文所采用的1/2模型如圖3所示。

圖 3　氣缸活塞沖擊端蓋有限元模型

活塞和活塞桿的材料為結構鋼，端蓋和缸筒的材料為鋁合金，有限元仿真時均采用線彈性材料模型。其材料性能參數見表1。

表 1　材料性能參數

氣缸裝配體模型均采用sweep掃掠方式劃分網格，網格均為八節點六面體單元。將缸筒與端蓋、活塞與活塞桿以及質量負載與活塞桿的連接設置成固連綁定接觸，活塞桿與端蓋導向環的相對滑動以及活塞與端蓋的碰撞接觸采用自動面面雙向接觸(ASTS)。將缸筒右端面和端蓋左端面設置成固定約束，將對稱面設置成對稱約束，保證活動部件可在對稱平面內平動。活塞桿與導向環、活塞與端蓋的摩擦因數均為0.1。在不考慮重力作用下，給活塞、活塞桿以及質量負載一定的初速度去沖擊端蓋，仿真得到碰撞沖擊響應。

為了有效地處理氣缸沖擊過程中的接觸問題、非線性問題和隨時間變化很快的沖擊力學過程，LS-DYNA求解器采用顯式直接積分方法，采用罰函數法處理沖擊過程中的動態接觸，并指定輸出RCFORC界面合力ASCII文件，獲得沖擊力的時間歷程曲線[11]。

氣缸在實際工作過程中，因應用場合不同，氣缸搭載的負載和運行速度就不一樣，運行到行程末端時，必然產生不同的沖擊情況。本文分析了氣缸在不同速度和不同質量下的沖擊狀況，得到了沖擊力響應曲線。

3　結果分析

本文研究的典型氣缸活塞桿直徑d=12 mm，活塞桿長l=193 mm，氣缸內直徑D=32 mm，端蓋長度l1=29 mm，活塞寬度l2=17 mm，活塞質量m=0.08 kg，仿真質量負載長度l3=50 mm，活塞與活塞桿質量比η=0.5，工作行程s=100 mm。

氣缸的碰撞為活塞與端蓋的短暫接觸，由于活塞長度較端蓋短，而其彈性模量比端蓋大得多，使得活塞的抗壓剛度比端蓋的抗壓剛度大得多，物理建模時將活塞看成一個集中質量，而將端蓋看成接觸彈簧；此外，由于活塞運行到行程末端時，有桿腔內氣體迅速排空，故忽略氣體對接觸剛度的耦合影響，其等效接觸剛度為

1.12×109(N/m)

其中，E1為端蓋材料彈性模量，Acon為活塞與端蓋碰撞有效接觸面積，碰撞處端蓋內半徑r=10.3 mm。

將上述參數代入解析解中，利用MATLAB編程計算，取前100階(已趨于穩定)模態疊加，得到理論解析曲線。

3.1沖擊力與速度的關系

為了驗證解析解表達式中沖擊力與沖擊速度的線性關系，在負載為20 N的情況下，分別取活塞沖擊速度為0.1 m/s、0.2 m/s、0.3 m/s、0.4 m/s、0.5 m/s進行有限元仿真計算，得到在不同速度下的沖擊力-時間曲線，如圖4所示。并將0.5 m/s沖擊速度下的仿真曲線與理論曲線進行對比，如圖5所示。

圖 4　不同速度下的沖擊力-時間曲線

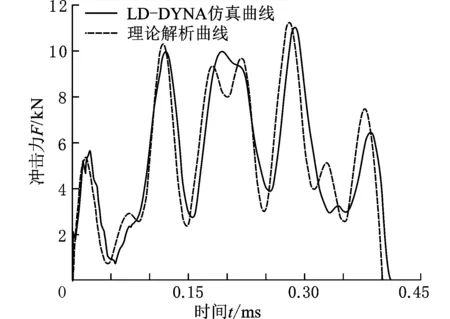
圖 5　仿真曲線與理論曲線對比(負載為20 N，沖擊速度為0.5 m/s)

從圖4可看出，在不同沖擊速度下，有限元仿真得到的沖擊力波形隨時間同步變化，且沖擊力隨速度線性增大；同時，還可以看出，在同一負載下，沖擊作用時間并不隨著沖擊速度的變化而變化，而是保持不變。從圖5可看出，同一沖擊條件下，LS-DYNA仿真曲線與理論解析曲線十分吻合，表明仿真結果與解析表達式一致，從而驗證了解析表達式中沖擊力與速度的關系。

3.2沖擊力與負載的關系

通過改變程序中質量比α的大小，得到一系列不同負載下的沖擊力響應曲線。同時，為了進一步研究活塞沖擊端蓋的沖擊情況，利用LS-DYNA仿真分析了負載分別為10 N、20 N(圖5)、30 N、40 N、50 N在沖擊速度為0.5 m/s時的沖擊過程，經過后處理得到沖擊力-時間歷程曲線。將相應的理論解析曲線與LS-DYNA仿真曲線進行對比分析，結果對比如圖6～圖9所示。

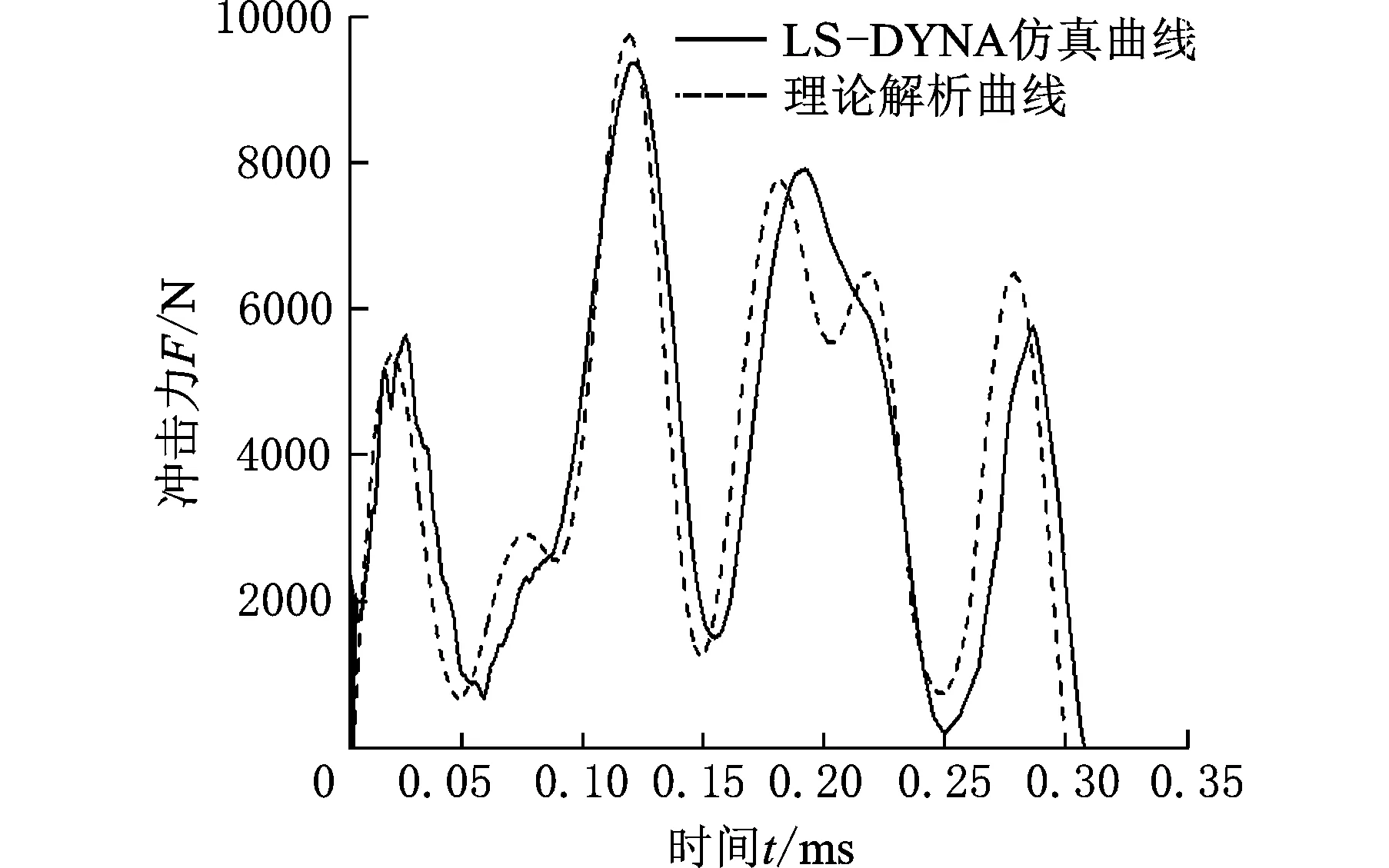
圖 6　仿真曲線與理論曲線對比(負載為10 N，沖擊速度為0.5 m/s)

圖 7　仿真曲線與理論曲線對比(負載為30 N，沖擊速度為0.5 m/s)

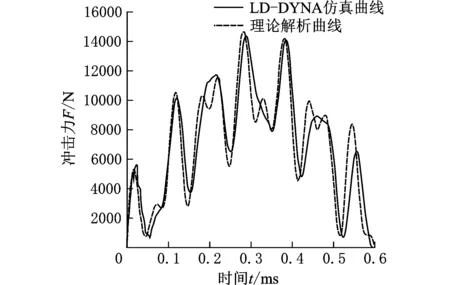
圖 8　仿真曲線與理論曲線對比(負載為40 N，沖擊速度為0.5 m/s)

圖 9　仿真曲線與理論曲線對比(負載為50 N，沖擊速度為0.5 m/s)

結合圖5～圖9，對比LS-DYNA仿真數值解與理論解析解可知，兩者得出的活塞沖擊面沖擊力時間歷程曲線在變化趨勢、峰值大小、峰值數量以及沖擊作用時間等方面，理論解析與有限元仿真十分吻合，進一步說明了上述物理模型建立以及模型簡化處理的正確性和可靠性。

同時，從圖6～圖9可以看出，沖擊力隨時間的變化曲線并不具有單峰值和完全對稱性，也并不是先增大后減小，而是表現為多峰值且與時間不對稱的波動形式。隨著負載質量的不斷增加，峰值和峰值個數也不斷增加，沖擊力曲線波動越來越“劇烈”，沖擊作用時間也不斷變長，這是由于振動頻率的變化所致。

3.3振動頻率分析

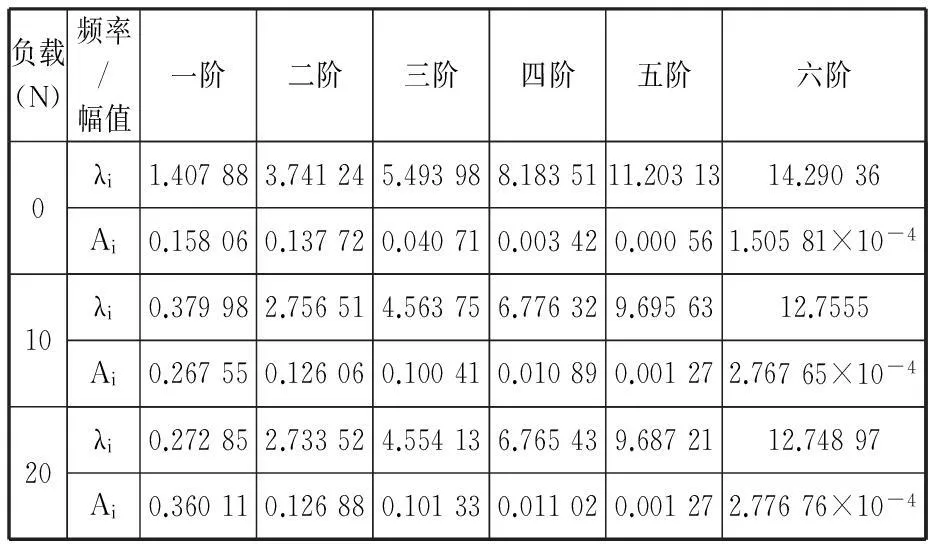
沖擊接觸面的振動為細長活塞桿各階主振動在桿碰撞端x=l處的疊加，其振動位移響應是由具有各階固有頻率的諧波信號組成的。不同負載質量下的前6階無因次固有頻率及相應的振幅見表2。

表2不同負載下沖擊處振動位移中前六階振動頻率與幅值

負載(N)頻率/幅值一階二階三階四階五階六階0λi1.407883.741245.493988.1835111.2031314.29036Ai0.158060.137720.040710.003420.000561.50581×10-410λi0.379982.756514.563756.776329.6956312.7555Ai0.267550.126060.100410.010890.001272.76765×10-420λi0.272852.733524.554136.765439.6872112.74897Ai0.360110.126880.101330.011020.001272.77676×10-4

從表2可以看出，隨著頻率階次的增加，其對應的幅值不斷衰減，且從第四階頻率開始，衰減得很快。同時，隨著負載質量的不斷增加，同一階次的頻率值有所減小，但同一階次的幅值有所增大，且第一階頻率和幅值對負載質量的變化最敏感。但是，隨著階數的增加，各階頻率值和幅值對負載質量的變化越來越不敏感，使得不同負載質量下的各階頻率值和幅值都十分接近。

負載質量的增加，使得振動位移響應中低頻(尤其是第一階頻率)成分所占比重不斷增加，從而導致沖擊力幅值的不斷增大；各階頻率的減小，使得沖擊作用時間不斷增大，沖擊力波動變化越來越“劇烈”。

在氣缸短暫劇烈的沖擊過程中，高頻響應衰減得十分迅速。為了使解析式進一步推廣到實際運用，在不增大負載質量的情況下，通過取前5階模態和前100階模態所得到的沖擊力解析曲線與LS-DYNA仿真曲線對比分析，如圖10所示。

圖10　仿真曲線與理論曲線對比(負載為0,沖擊速度為0.5 m/s)

圖10結果顯示,三條曲線十分吻合；同時,模態階數的減少,使得沖擊力幅值和沖擊作用時間稍有延長。但隨著負載質量的增加，兩種階次取值所得到的沖擊力響應曲線趨于重合，差距完全可以忽略不計。這是由于隨著負載質量的增加，高頻成分衰減得越來越迅速，高階振型中基本不引起振動。因此，實際工程運用(如螺紋連接設計所考慮的最大沖擊力、端蓋螺紋孔的大小和深度以及安裝方式)中，只需要考慮前面幾階振型分析就足夠準確了。

4　結論

(1)本文對氣缸行程末端活塞沖擊端蓋的現象進行動力學建模，將其看成一個振動系統，采用模態分析方法推導出沖擊力響應解析解，計算結果與LS-DYNA仿真分析結果吻合，證明了本文簡化建模及其解析解的正確性。

(2)沖擊力與活塞沖擊速度成線性關系；隨著負載質量的增加，沖擊力幅值不斷增大，且波動得更“劇烈”。沖擊作用時間隨負載質量的增加而變長，但與與沖擊速度無關。

(4)沖擊響應中第一階模態對負載變化最敏感，但隨著階次的增加，高階模態對負載變化越來越不敏感；同時，高階頻率成分衰減得很快，實際運用中只需要取幾階低頻分析即可。

(5)研究結果為氣缸的可靠性研究提供了理論依據，為氣缸的結構(尤其是緩沖結構)設計、活塞螺紋連接、使用安裝、維護保養提供了理論依據和數據支持。

[1]廖理.沖擊負載下氣缸性能測試平臺的研究與實現[D].成都:電子科技大學,2013.

[2]Love A E H. A Treatise on the Mathematical Theory of Elasticity [M].New York: Dover, 1994.

[3]張繼業,曾京,舒仲周.桿的縱向沖擊振動[J].振動與沖擊, 1999,18(3):58-63.

Zhang Jiye,Zeng Jing,Shu Zhongzhou.Longitudinal Vibration of Prismatic Bar during Impact[J].Journal of Vibration and Shock,1999,18(3):58-63.

[4]Gan Chunbiao, Wei Yimin, Yang Shixi. Longitudinal Wave Propagation in a Rod with Variable Cross-section[J]. Journal of Sound and Vibration, 2014,333(2) :434-445.

[5]諸德超,邢譽峰. 點彈性碰撞問題之解析解[J].力學學報, 1996,28(1):99-103.

Zhu Dechao, Xing Yufeng. Analytical Solution of Point Elastic Impact between Structures[J].Chinese Journal of Theoretical and Applied Mechanics,1996, 28(1):99-103.

[6]吳家強,王宏志. 桿的縱向沖擊問題全過程分析[J]. 振動與沖擊,2004,23(1):103-106.

Wu Jiaqiang, Wang Hongzhi. General Procedure for Analysis of Axial Response of Prismatic Bar during Impact[J].Journal of Vibration and Shock, 2004, 23(1):103-106.

[7]鮑四元. 彈性碰撞問題的模態疊加法及哈密頓體系下的計算研究[D].西安:西北工業大學,2005.

[8]Li Q S,Wu J R, Xu J. Longitudinal Vibration of Multi-step Non-uniform Structures with Lumped Masses and Spring Supports[J]. Applied Acoustics,2002,63(3):333-350.

[9]孫龍.潛孔錘及聲波鉆柔體振動沖擊的理論與建模[D].北京:中國地質大學,2014.

[10]倪振華.振動力學[M].西安:西安交通大學出版社,1990.

[11]王澤鵬,胡仁喜,康士廷,等.ANSYS14.5/LS-DYNA非線性有限元分析實例指導教程[M].北京:機械工業出版社,2013.

(編輯陳勇)

Impact Dynamics Modeling and Simulation Analyses of Pneumatic Cylinders

Du QunguiSun ZhiquanHuang ChongxiZhai Xiaochen

South China University of Technology,Guangzhou,510640

Impact of pneumatic cylinder at the stroke terminal was considered to be an integrated system of vibrations, including slender piston rod, mass load, piston and end cover.Based on one-dimensional wave equation, a mathematical model of longitudinal vibration of slender piston rod was established firstly. Impact force,contact displacement and contact time were analyzed by means of mode superposition method.Then impact process of pneumatic cylinder was numerically simulated by nonlinear FEM software LS-DYNA.The variation of impact interface force and contact time were studied in detail under different masses of driven load and impact velocities. Compared with numerical solution of LS-DYNA,the accuracy of analytical solution was verified, and how impact force varies as velocity and load was concluded. Vibration frequencies of impact response were furtherly analyzed, and reasons for the changes of impact forces were studied. Research conclusions provide reference for design and applications of pneumatic cylinders.

impact force of pneumatic cylinder; analytical solution; LS-DYNA simulation; frequency analysis

杜群貴,男,1965年生。華南理工大學機械與汽車工程學院教授、博士研究生導師。主要研究方向為現代機電工程設計與控制。孫智權，男，1991年生。華南理工大學機械與汽車工程學院碩士研究生。黃崇溪，男，1990年生。華南理工大學機械與汽車工程學院碩士研究生。翟曉晨，男，1988年生。華南理工大學機械與汽車工程學院博士研究生。

2015-04-10

TH138.51;O326

10.3969/j.issn.1004-132X.2016.08.011