隨機-認知不確定性的相關性分析模型及可靠性計算方法
鄭 靜 姜 潮 倪冰雨 范 松
湖南大學汽車車身先進設計制造國家重點實驗室,長沙,410082
?
隨機-認知不確定性的相關性分析模型及可靠性計算方法
鄭靜姜潮倪冰雨范松
湖南大學汽車車身先進設計制造國家重點實驗室,長沙,410082
針對工程中同時存在隨機和認知不確定性的問題,提出了一種考慮相關性的概率-證據混合不確定性模型及相應的結構可靠性分析方法。首先引入樣本相關系數來描述概率變量之間、證據變量之間以及概率和證據變量之間的相關性,通過一個轉換矩陣將原問題中相關的變量轉換為相互獨立的變量,并構建了一個等效的概率-證據混合可靠性模型。然后將其轉化為一系列概率-區間混合可靠性分析模型,并總結了嵌套優化分析迭代格式來求解失效概率區間。最后提供了三個數值算例驗證該方法的有效性。
混合可靠性;隨機不確定;認知不確定;樣本相關系數
0 引言
工程實際中經常存在著與材料特性、邊界條件和載荷等有關的各種不確定性[1],隨著對產品可靠性、安全性、穩定性要求的提高,基于不確定性的設計與分析方法得到了廣泛的研究與應用。不確定性通常可分為隨機不確定性和認知不確定性[2-3]。隨機不確定性(又稱統計不確定性或客觀不確定性)主要描述系統內在的變化,通常用概率模型進行描述,目前已發展出一些成熟的可靠性分析方法,如一次二階矩(FORM)[4-5]、二次二階矩(SORM)[6]、蒙特卡羅仿真[7]、基于可靠性的優化設計(RBDO)[8-9]等。認知不確定性(又稱主觀不確定性)主要源于信息不完備、認識水平局限和知識缺乏,可用非概率模型來進行描述。目前用于解決認知不確定性的常用方法有證據理論(或Dempster-Shafer理論)[10-11]、可能性理論[12]、模糊理論[13]和凸模型理論[14-15]等。
證據理論是一種較為一般的不確定性理論,能靈活處理各類認知不確定性,在某些特殊情況下可等效于概率理論、可能性理論、模糊理論和凸模型理論等。近年來證據理論在結構可靠性分析方面得到了越來越多的關注,也取得了一系列的研究成果。Helton等[16]通過簡單的代數函數研究了證據理論在工程可靠性中的應用,并探討了其優缺點。Tonon[17]通過分析不同參數類型,應用證據理論討論了在認知不確定的情況下機械系統對于不確定參數的響應。Guo等[18]提出了一種考慮權重平衡的證據理論,用于識別結構多損傷位置。Mourelatos等[19]提出了一種基于證據理論的高效可靠性優化方法(EBDO)。Simon等[20]介紹了貝葉斯網絡在可靠性分析中的應用,并利用證據理論來處理可靠性問題中的認知不確定性。Jiang等[21]采用證據變量均勻化的方法,提出了一種高效的可靠性分析方法。Bai等[22]比較了三種代理模型在證據理論可靠性分析中的準確性與穩定性。
在實際工程問題的結構中可能同時存在著隨機不確定性和認知不確定性,此時用單一的概率模型或者證據模型來描述所有變量,都會影響結構可靠性分析的精確度,因此建立概率-證據混合不確定性分析模型十分必要。目前,已有少量概率-證據混合可靠性分析的研究成果出現。Du等[23-24]建立了一個統一分析框架來解決隨機不確定和認知不確定同時存在的問題,并在此基礎上提出了一種靈敏度分析方法。Tao等[25]針對同時包含隨機不確定性和認知不確定性的多目標系統提出了一種新型可靠性分析方法。Li等[26]基于概率模型和證據模型,通過構建二級極限狀態方程及相應的可靠性分析方法求解了同時包含隨機不確定性及認知不確定性結構的失效概率。但是,目前的隨機-認知不確定混合可靠性分析模型主要是針對獨立變量,而在實際工程問題中,變量之間可能是相關的,且相關性經常對結構的可靠性具有重要影響。直接假設變量之間相互獨立則可能會導致較大的計算誤差,使得結果不符合結構可靠性設計的高精度要求。因此,本文提出了一種考慮相關變量的混合不確定模型,以求解該類可靠性分析問題。
1 證據理論基本原理
D-S證據理論(Dempster-Shafer theory of evidence/evidential theory)是在Dempster提出的“上下概率”及其合成規則的基礎之上,由Shafer進一步發展起來的。建立證據理論的數學模型首先應確立識別框架Θ,將命題的研究轉化為對集合的研究。識別框架指人們能認識到的所有可能結果的集合,類似于概率模型中的采樣空間,由有限的元素組成。令2Θ表示識別框架Θ的冪集,由Θ包含的所有可能的不同命題組成。證據理論利用基本可信度分配BPA(basic probability assignment)來表示對某一命題A的信任程度。BPA為一個滿足如下三條性質的映射M:
M(A)≥0,?A∈2X
(1)
(2)
M(φ)=0
(3)
其中,M(A)>0的集合A叫作M的焦元。M(A)反映了對命題A本身信度的大小,類似于隨機模型中的概率密度函數[19]。當同一識別框架上具有多個不同來源的證據時,需根據Dempster-Shafer合成法則[10](簡稱D-S合成法則)對證據進行合成以形成對命題的總支持度。
由于信息的缺乏,證據理論無法獲得命題A的精確概率,因此使用區間測度來描述命題的真實程度。區間測度下界Pbel(A)和上界Ppl(A)分別稱為可信度和似真度,其定義如下:
(4)
(5)
可見,Pbel(A)是完全支持命題A的基本可信度之和,Ppl(A)則是完全或者部分支持命題A的基本可信度之和。這兩個測度構成的區間[Pbel(A),Ppl(A)]稱為命題A的信任區間。
2 概率-證據相關性分析模型
在統計理論中,線性相關系數是描述兩個隨機變量之間相關程度最簡單且常用的度量方法[27]。對于隨機變量X1和X2,其相關系數ρX1X2定義如下:
(6)
式中,Var(X1)和Var(X2)分別表示變量X1與X2的方差;Cov(X1,X2)表示變量X1和X2的協方差。
相關系數ρX1X2反映了兩個變量X1和X2的線性相關程度,對于特定的總體來說,相關系數是客觀存在的特定數值。但是,一般很難觀測到總體的所有樣本,因此人們通常通過已有的樣本觀測值來估計變量之間的樣本相關系數。rX1X2=rX2X1表示X1和X2之間的樣本相關系數:
(7)
k=1,2,…,w

(8)
可見,樣本相關系數的計算并不依賴于變量的分布形式,因此對于不同的不確定性變量,只要已知樣本的信息,就可以得到變量之間的樣本相關系數。故隨機變量之間、證據變量之間以及隨機變量與證據變量之間的相關性都可以用統一的形式來描述。將樣本相關系數的概念拓寬到概率-證據混合不確定性問題中,能有效處理多種不確定變量之間的相關性。如果有m維隨機向量X=(X1,X2,…,Xm)和n維證據向量Y=(Y1,Y2,…,Yn),則任意兩個變量之間的樣本相關系數可由式(7)獲得,最終可建立(X,Y)的樣本相關系數矩陣如下:
rXY=
(9)
3 結構可靠性分析
假設一結構中含m維隨機向量X=(X1,X2,…,Xm)和n維證據向量Y=(Y1,Y2,…,Yn),考慮如下的極限狀態方程:
g=g(X,Y)
(10)

3.1仿射坐標變換
樣本相關系數矩陣rXY可進行如下分解
rXY=ATA
(11)
根據Cholesky分解[29]可知,有且僅有唯一的上三角矩陣滿足上述分解:
(12)
通過矩陣A將原變量轉化為V=(V1,V2,…,Vm+n),即
V=A(X,Y)
(13)
故
(X,Y)TrXY(X,Y)=(A-1V)TrXY(A-1V)=
VT[(A-1)TrXYA-1]V
(14)
(A-1)TrXYA-1=(A-1)TATAA-1=I
(15)
可見,轉換后V=(V1,V2,…,Vm+n)為相互獨立的變量,且轉換后的變量可由原變量線性表示出:
(16)



(17)


(18)
(19)

3.2失效概率求解

(20)
由全概率公式,結構失效概率可按下式計算[23-24]:


(21)
(22)

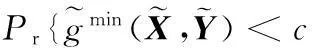
(23)


(24)

(25)
(26)

(27)
(28)



(29)
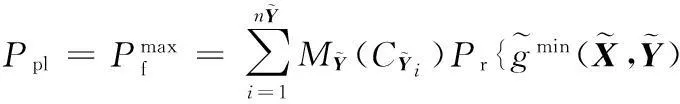
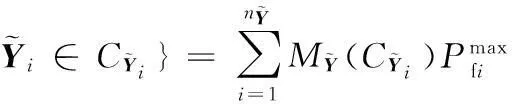
(30)
3.3嵌套優化分析
根據3.2節所述,首先將概率-證據混合可靠性問題轉化為一系列概率-區間混合可靠性問題,對于每一個概率-區間混合問題,通過構造一高效的序列迭代格式[30]進行求解,每次迭代依次進行概率分析和區間分析,最終使內外層同時達到穩定解。
U(k+1)=U(k)+αd(k)
(31)
其中,α為迭代步長,由最小化價值函數v確定;d(k)為搜索方向:
(32)
(33)

(34)
其中,h為常數。
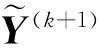
(35)
4 算例分析與應用
4.1數學算例
考慮如下的極限狀態方程:
(36)
其中,X1、X2為概率變量;Y1為證據變量。變量的分布類型和分布參數如表1所示。

表1 變量的分布類型和分布參數(數學算例)
注:在正態分布中,參數1為均值,參數2為標準差,在證據變量中,參數1為證據變量子區間,參數2為相應的BPA值。
假設通過樣本求得的樣本相關系數矩陣為
(37)
通過求解不同閾值c下的結果,可以得到對應的Pbel和Ppl,可靠性分析結果如圖1與表2所示。從圖表中可見,隨著閾值的升高,Pbel和Ppl的值從0增加到1.0,且Pbel和Ppl函數曲線均為連續的曲線,而不是僅存在證據變量時所呈現的階梯曲線,表明由于輸入變量中概率變量的存在,可靠性不再發生階躍突變,而是隨c值連續變化。

圖1 可靠性分析結果曲線(數學算例)

閾值c436439442445448451可信度0.00000.00000.00000.00010.00140.0095似真度0.00000.00000.00030.00290.01690.0643閾值c454457460463466469可信度0.04160.12630.28280.49660.71600.8800似真度0.17260.35050.57090.77680.91520.9780閾值c472475478481484可信度0.96460.99310.99910.99991.0000似真度0.99630.99961.00001.00001.0000
本算例中分析了三種情況,每種情況中僅有其中一組變量之間存在相關性,而其他變量之間均相互獨立。假設樣本相關系數在[-1,1]之間變化,得出三組在不同樣本相關系數情況下結構失效概率的變化曲線,如圖2所示。整體而言,Pbel和Ppl的值隨相關系數變化而有明顯的變化,可見該數學算例中變量之間的相關性對可靠性分析結果有著較明顯的影響。在圖2a中,rX1X2從-0.9變化到0.9,Ppl值從0.4306降至0.4153,Pbel值從0.0572降至0.0335,失效概率上下界均沒有明顯變化。在圖2b和圖2c中,隨著樣本相關系數的變化,失效概率有較明顯的變化。由圖2b可見,隨著rX1Y1由-0.9變化到0,Ppl從0.6184降至0.4213,減小了31.9%;隨著rX1Y1由0變化到0.9,Ppl從0.4213緩慢至到0.4427,增大了5.1%;Pbel值在不同rX1Y1的情況下有微小的波動。圖2c中Ppl值的變化呈U字形;Pbel值在不同rX2Y1的情況下變化較小,基本維持在一個穩定值。從這三個圖中可以看到,該算例中不同的變量之間的相關性對可靠性分析結果有不同幅度的影響,且變量X2和Y1之間的相關性對可靠性的結果影響最為顯著。

(a)樣本相關系數rX1X2與失效概率Pf的關系

(b)樣本相關系數rX1Y1與失效概率Pf的關系

(c)樣本相關系數rX2Y1與失效概率Pf的關系圖2 失效概率與變量之間相關性的關系(數學算例)
4.2懸臂梁

圖3 懸臂梁
如圖3所示,懸臂梁長度為L,橫截面寬度為b,高度為h,懸臂梁的頂端承受作用力Fx和Fy。懸臂梁的幾何尺寸L、b、h為概率變量,外力Fx、Fy為證據變量,其分布類型及取值如表3所示。當材料的許用應力σ與懸臂梁固定端處最大應力的差值小于閾值c時結構失效,即

(38)
注:在正態分布中,參數1為均值,參數2為標準差;在證據變量中參數1為證據變量子區間,參數2為相應的BPA值。
在該懸臂梁結構中,假設各個相關變量之間的樣本相關系數rbh=0.3,rbL=0.1,rhL=rFxFy=0.2,改變閾值c,得到對應的Pbel和Ppl如圖4所示。與圖1相比,Pbel函數和Ppl函數曲線之間的間距較小,可見與上一數學算例相比,本算例中認知不確定性對可靠性分析結果的影響較小。

圖4 可靠性分析結果曲線(懸臂梁)
另外,為分析變量之間的相關性對結構可靠性的影響,分別考慮了僅有橫截面寬度b與高度h之間以及外力Fx與Fy之間存在相關性的兩種情況,如圖5所示。從圖5中的變化曲線可看出,變量之間的相關性對結構可靠性有著一定的影響。圖5a中,隨著樣本相關系數rbh的變化,失效概率Pf的變化趨勢呈拋物線狀:即Ppl值先減后增,先從0.3403降至0.1574,下降幅度為53.7%,而后又增至0.3181,上升幅度為102.1%;Pbel值亦先增后減,先從0.3142降至0.1182,減小了62.4%,而后又增至0.2901,增大了145.4%。圖5b中,Ppl及Pbel的變化趨勢呈X形,失效概率的變化微小,其波動值最大分別為0.0207與0.0158。在該算例中,結構的失效概率隨變量之間相關性的不同而有所不同,且寬度b與高度h之間的相關性對結構可靠性的影響較大。

(a)樣本相關系數rbh與失效概率Pf的關系

(b)樣本相關系數rFxFy與失效概率Pf的關系圖5 失效概率與變量之間相關性的關系(懸臂梁)
4.3轉動導桿機構
如圖6所示的轉動導桿機構常常用于結構機構中,在高速單張紙印刷機的輸紙系統、回轉柱塞泵、葉片泵和旋轉式發動機等機器上都有應用,在實際工況中,對轉動導桿機構進行可靠性分析有重要的工程意義。在轉動導桿機構中,構成移動副的構件1和2的長度是不定的,曲柄3和機架4的長度可以測量。轉動導桿機構實現變速功能的機構是主動件做勻速轉動,從動件做變速轉動,從而滿足特定的工藝動作要求。主動件曲柄3繞軸A的整周勻速轉動,通過轉動導桿1和連桿5驅動切削頭6上固定的插刀,完成往復切削運動(切削行程較慢,回程較快)。轉動導桿1的BE段長度為l1,曲柄3的長度為l3,機架4的長度為l4,連桿5為空心圓管,其長度為l5,偏心距的長度為e,桿件材料的彈性模量為E,屈服強度σ=350 MPa,在做變速運動過程中滑塊6受到外部集中力F=250 kN作用,具體輸入參數如表4所示。滑塊與地面之間的摩擦因數μ=0.018。

圖6 轉動導桿機構

不確定變量參數1參數2分布類型l1(mm)1001正態l5(mm)3001正態d1(mm)300.5正態d2(mm)500.5正態e(mm)[100,120][120,140][140,150]0.20.50.3證據
注:在正態分布中,參數1為均值,參數2為標準差;在證據變量中參數1為證據變量子區間,參數2為相應的BPA值。
主動件曲柄3繞軸A的整周勻速轉動,當轉動導桿1和連桿5重合時,連桿5所受力最大,此時對應的應力為最大值:
(39)
考慮空心連桿5的強度失效,其極限狀態方程可以表示為
G=σ-σmax (40) 圖7 可靠性分析結果曲線(轉動導桿機構) 在該轉動導桿算例中,假設變量l1與l5以及d1與d2的樣本相關系數rl1l5= 0.1,rd1d2= 0.2,而其他變量之間均相互獨立,求得不同閾值c對應的Pbel和Ppl,如圖7所示。圖中Pbel和Ppl函數曲線之間存有較大的間距,說明該算例中認知不確定對結構可靠性影響較大。 為分析變量之間相關性對該轉動導桿結構的影響,現分別考慮轉動導桿l1與連桿l5以及連桿l5與偏心距e之間具有相關性的兩種情況,失效概率隨樣本相關系數的變化趨勢如圖8所示。圖8a中失效概率Pf值在rl1l5變化過程中基本保持不變,波動值不大于0.0003。圖8b中失效概率Pf值的變化相對較明顯:隨著rl5e從-0.9變化到0.9,Ppl值總體呈增長趨勢,且增長的速率由慢變快;Pbel值也緩慢從0.0066增至0.0233。 (a)樣本相關系數rl1l5與失效概率Pf的關系 (b)樣本相關系數rl5e與失效概率Pf的關系圖8 失效概率與變量之間相關性的關系(轉動導桿機構) 本文針對同時存在隨機和認知不確定性的問題,提出了一種考慮相關性的概率-證據混合不確定性模型及相應的結構可靠性分析方法。該方法通過引進樣本相關系數定義變量之間的相關性,并進行仿射變換,將原問題等效轉換為獨立變量的可靠性問題進行求解。三個數值算例驗證了本文提出的可靠性分析方法能有效處理同時存在隨機和認知不確定性的問題。算例的結果分析表明,在很多情況下,變量之間的相關性對可靠性有較明顯的影響,且不同變量之間的相關性對可靠性結果的影響不同。因此,為了提高隨機-認知混合可靠性分析的精度,考慮變量之間的相關性非常重要。 [1]Guo J, Du X P.Sensitivity Analysis with Mixture of Epistemic and Aleatory Uncertainties[J]. AIAA Journal,2007, 45(9): 2337-2349. [2]Rowe W D.Understanding Uncertainty[J]. Risk Analysis, 1994,14(5):743-750. [3]Helton J C. Uncertainty and Sensitivity Analysis in the Presence of Stochastic and Subjective Uncertainty[J]. Journal of Statistical Computation and Simulation,1997,57(1/4):3-76. [4]Hasofer A M, Lind N C. Exact and Invariant Second-moment Code Format[J]. Journal of the Engineering Mechanics Division, 1974, 100(1): 111-121. [5]Rackwitz R, Fiessler B. Structural Reliability under Combined Random Load Sequences[J]. Computers & Structures, 1978, 9(5): 489-494. [6]Breitung K W. Asymptotic Approximation for Multinormalintegrals[J]. Journal of Engineering Mechanics, 1984, 110(3): 357-366. [7]Rubinstein R Y, Kroese D P. Simulation and the Monte-Carlo Method[M]. 2nd ed. New York: Wiley,2007. [8]Du X P, Chen W. Sequential Optimization and Reliability Assessment Method for Efficient Probabilistic Design[J]. Journal of Mechanical Design, 2004, 126(2):225-233. [9]Liang J H, Mourelatos Z P, Nikolaidis E. A Single-Loop Approach for System Reliability-based Design Optimization[J]. Journal of Mechanical Design, 2007, 129(12):1215-1224. [10]Shafer G. A Mathematical Theory of Evidence[M]. Princeton, NJ:Princeton University Press,1976. [11]Dempster A P.Upper and Lower Probabilities Induced by a Multivalued Mapping[J].The Annals of Mathematical Statistics, 1967,38(2): 325-339. [12]Klir G J. Generalized Information Theory: Aims, Results, and Open Problems[J]. Reliability Engineering & System Safety, 2004, 85(1): 21-38. [13]Zadeh L A. Fuzzy Sets[J]. Information and Control, 1965, 8(3): 338-353. [14]Ben-haim Y, Elishakoff I. Convex Models of Uncertainty in Applied Mechanics[M]. Amsterdam: Elsevier, 1990. [15]Qiu Z P, Yang D, Elishakoff I. Probabilistic Interval Reliability of Structural Systems[J]. International Journal of Solids and Structures, 2008, 45(10):2850-2860. [16]Helton J C,Oberkampf W L.Alternative Representations of Epistemic Uncertainty[J]. Reliability Engineering and System Safety, 2004,85(1/3):1-10. [17]Tonon F.Using Random Set Theory to Propagate Epistemic Uncertainty through a Mechanical System[J]. Reliability Engineering and System Safety, 2004,85(1/3):169-181. [18]Guo H Y, Zhang L. A Weighted Balance Evidence Theory for Structural Multiple Damage Localization[J]. Computer Methods in Applied Mechanics and Engineering, 2006, 195(44): 6225-6238. [19]Mourelatos Z P, Zhou J. A Design Optimization Method Using Evidence Theory[J]. Journal of Mechanical Design, 2006,128(4): 901-908. [20]Simon C, Weber P, Evsukoff A. Bayesian Networks Inference Algorithm to Implement Dempster Shafer Theory in Reliability Analysis[J]. Reliability Engineering & System Safety, 2008, 93(7): 950-963. [21]Jiang C, Zhang Z, Han X.A Novel Evidence-theory-based Reliability Analysis Method for Structures with Epistemic Uncertainty[J]. Computers & Structures, 2013, 129:1-12. [22]Bai Y C, Han X, Jiang C, Liu J.Comparative Study of Metamodeling Techniques for Reliability Analysis Using Evidence Theory[J]. Advances in Engineering Software,2012, 53:61-71. [23]Du X P. Uncertainty Analysis with Probability and Evidence Theories[C]//ASME 2006 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference. Philadelphia,2006: 1025-1038. [24]Du X P. Unified Uncertainty Analysis by the First Order Reliability Method[J]. Journal of Mechanical Design, 2008, 130(9): 091401. [25]Tao Y R, Han X, Duan S Y, et al.Reliability Analysis for Multidisciplinary Systems with the Mixture of Epistemic and Aleatory Uncertainties[J]. International Journal for Numerical Methods in Engineering,2014,97(1):68-78. [26]Li G J, Lu Z Z, Lu Z Y, et al.Regional Sensitivity Analysis of Aleatory and Epistemic Uncertainties on Failure Probability[J]. Mechanical Systems and Signal Processing, 2014, 46(2): 209-226. [27]Barlow R E, Proschan F.Statistical Theory of Reliability and Life Testing: Probability Models[R]. New York: Holt, Rinehart, and Winston,1975. [28]Iversen G R, Gergen M,Gergen M M.Statistics: the Conceptual Approach[M]. Berlin:Springer Science & Business Media,1997. [29]Pozrikidis C. Numerical Computation in Science and Engineering[M]. New York: Oxford University Press,1998. [30]Du X P. Interval Reliability Analysis[C]//ASME 2007 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference. Las Vegas, 2007: 1103-1109. [31]Zhang Y, Kiureghian A D.Two Improved Algorithms for Reliability Analysis[M]. New York:Springer U.S., 1995. [32]Jiang C, Li W X, Han X, et al.Structural Reliability Analysis Based on Random Distributions with Interval Parameters[J].Computers & Structures, 2011, 89(23): 2292-2302. (編輯王旻玥) An Aleatory and Epistemic Mixed Uncertainty Model Considering Parametric Correlation and Its Reliability Analysis Zheng JingJiang ChaoNi BingyuFan Song State Key Laboratory of Advanced Design and Manufacturing for Vehicle Body, Hunan University,Changsha,410082 A probability and evidence hybrid uncertainty model considering parametric correlation was proposed and a corresponding reliability analysis method for problems with both aleatory and epistemic uncertainties was studied.Firstly,sample correlation coefficients were introduced to describe the correlation among probability variables,evidence variables as well as probability and evidence variables. Correlated parameters were transformed into independent ones through a matrix transformation and an equivalent probability-evidence hybrid model was built. Then the hybrid model was transformed into a series of probability-interval models in subspaces and a nested optimization analysis iterative format was summarized to obtain the failure probability interval. At last, three numerical examples were provided to verify the validity of the proposed method. hybrid reliability;aleatory uncertainty;epistemic uncertainty;sample correlation coefficient 2015-03-18 國家自然科學基金資助項目(11172096,51222502);霍英東基金資助項目(131005);湖南省杰出青年基金資助項目(14JJ1016) TB114.3DOI:10.3969/j.issn.1004-132X.2016.07.013 鄭靜,女,1990年生。湖南大學機械與運載工程學院博士研究生。主要研究方向為結構可靠性設計。姜潮,男,1978年生。湖南大學機械與運載工程學院教授、博士研究生導師。倪冰雨,男,1989年生。湖南大學機械與運載工程學院博士研究生。范松,男,1989年生。湖南大學機械與運載工程學院碩士研究生。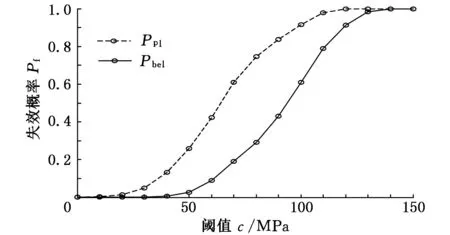


5 結論

