數(shù)值方法研究諧振子勢阱和磁場中的帶電荷玻色氣體
李玉山
(1.菏澤學院物理系,菏澤274015;2.北京科技大學物理系,北京100083)
1 Introduction
For many years,thermodynamic properties of uniform charged Bose gases(CBGs)have been extensively studied in the context of trapped cold atoms[1-5].Ultra-cold atomic gases are usually confined in a trap,the simplest is the harmonic potential because of its mathematical simplicity.Since the density of states(DOS)is modified by the trapping effect,the thermo-dynamical behaviors of trapped bosons undergoing Bose –Einstein condensation (BEC)can be altered by the spatially varying trapping potential.The BEC under an external potential behaves very distinctly from the homogeneous condensate[6-9]. The trapped CBGs reveal some typical features,for example,we can add angular momentum to the system with the rotation effect so that it could be compared with the orbital motion of charged particle subjected to a uniform magnetic field.Furthermore,the orbital motion of charged particles can give rise to a sizable diamagnetism and Meissner effect,especially focusing on the region of sufficiently low temperature[4-5].
More recently,thermodynamics of charged ideal Bose gases confined in harmonic potential and magnetic field have been discussed based on Thomas-Fermi approximation(TFA),in which the sum over the discrete spectrum for the thermodynamic quantities is replaced by aphasespace integral with an appropriate density of states[10].The studies indicate that Laudau diamagnetism appears and keeps invariant at all temperatures through applying the Poisson formula to the thermodynamic potential. Thermodynamic quantities,such as the transition temperature and heat capacity,also result in some debated questions.Motivated by these remarkable and strange findings in Ref.[10],we present a standard numerical method to investigate thermodynamics of CBGs.We calculate numerically thermodynamic quantities of the system and compare them with TFA.In addition to the consistency with TFA results,our numerical calculation also obtains some intriguing results superior to the TFA.Hereafter,we set the fundamental constants as?=kB=c=1in the following.
2 Theoretical model and numerical procedure
We consider a system of Nbosons with single particle mass mand charge qtrapped in an anisotropic harmonic potential under a constant magnetic field perpendicular to the plane of confinement.The non-interacting total Hamiltonian of the system is simply a sum of single particle operators,describing by

Here,A→is an effective vector potential,ω0andωzrepresent the frequencies of confining potential in the x - y plane and z direction,respectively[11-12].
The spectrum of the single particle Hamiltonian has the following form

whereωBdenotes the Larmor frequency,which is a half of the cyclotron frequency.The quantum numbers nandαcorrespond to radial and angular,whileνis that along zdirection.
By means of the Poisson formula[13-15],the analytical expressions of thermodynamic quantities can easily be derived from TFA method[10,16].Next,we describe the standard procedure of numerical calculation as follows.We calculate the chemical potentialμ first by solving the equation

where Tdenotes the temperature of the system.And then,compute the BEC transition temperature,internal energy,specific heat,magnetization and magnetic susceptibility through their respective equations in Ref.[10].
3 Results and discussion
The numerical results are shown from Figs.1to 8withω0/ωz=0.9.The number of bosons is fixed to 1000.All the summation quantum numbers are cutoff at 1000.The dimensionless temperature,chemical potential and internal energy are defined as in units ofωzfor clarity.For comparison,we calculate both Thomas-Fermi approximation(denoted by TFA)and numerical(denoted by NUM)results in the same chart.
In Fig.1,we read off that dimensionless BEC temperature increases along with the enlargement of particle number.The TFA results calculated by classical Hamiltonian are irrelevant to external magnetic field,while the NUM results suggest that BEC transition temperature decreases slightly as the magnetic field is strengthened.Oblivi-ously,the numerical method is more suitable for our physical model and established intuition[17].The discrepancy between TFA and NUM become larger as the bosons number and the magnetic field are increased,showing that the accuracy of the TFA method becomes worse for larger atoms number and stronger magnetic field.This deviation may be resulted from the quantum effect which is neglected in TFA.From Fig.2we can see that the dimensionless chemical potential is only determined by the temperature and particle number,having no relation with the magnetic field.That is to say,the influence of magnetic field on BEC temperature mainly comes from the energy level in Eq.(2).
In order to make the temperature effect clear,we calculated the condensate fraction,total energy and heat capacity versus the reduced temperature,which is reduced to the TFA value.Fig.3shows that the condensate fraction depends on both the temperature and magnetic field.Below BEC temperature,as the temperature decrease,the number of condensate particles increase.When the temperature comes close to the absolute zero temperature,all the non-interacting bosons will condense into their quantum mechanical ground states.The per-particle total energy shown in Fig.4suggests that there is a distinct jump near the critical temperature.The significant phase transition deserves our more attention to this system.The NUM results of heat capacity in Fig.5are slightly different from TFA due to the influence of magnetic field.The differences among them nearby critical temperature are prominent,implying that there exists a different phase transition.The heat capacity tends to a classical constant at the region of higher temperature,demonstrating that the total energy and heat capacity have a good agreement with energy equipartition theorem and Dulong-Petit law.
As can be seen from Figs.6and 7,the negative magnetization reflects that CBGs exhibit diamagnetism.Moreover,the diamagnetism varies with the temperature and external field,different with the conclusions reported by Ref.[10].It is gradually strengthened as lower temperature and stronger magnetic field.The temperature and magnetic field dependences for magnetization are also confirmed by the magnetic susceptibility shown in Fig.8.Meanwhile,this characteristic of magnetization proves that the TFA is invalid to deal with magnetic properties of trapped atoms due to its simplicity in certain conditions[18],especially when the system appears distinct quantum character.Under the higher temperature,both magnetization and magnetic susceptibility tend to become a consistent constant,meaning that the influence of magnetic field can be ignored.As the temperature goes higher,the numerical method also begins to lose its effectiveness and precision.
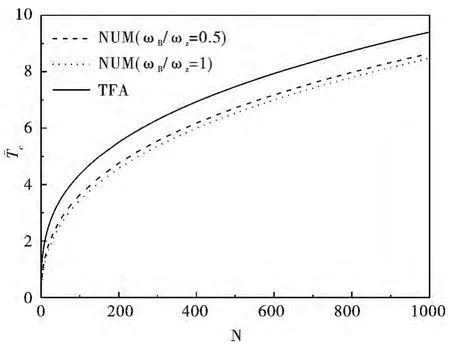
Fig.1 The dimensionless BEC temperature versus particle number
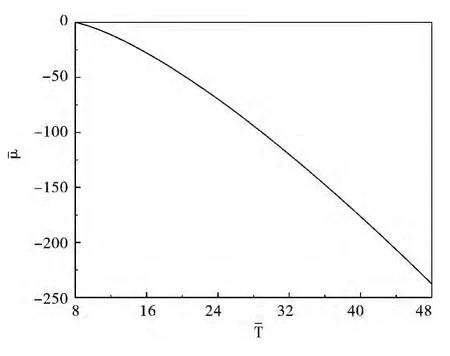
Fig.2 Dimensionless chemical potential versus temperature

Fig.3 Condensate fraction versus the reduced temperature

Fig.4 Total energy of single particle versus the reduced temperature

Fig.5 Heat capacity versus the reduced temperature
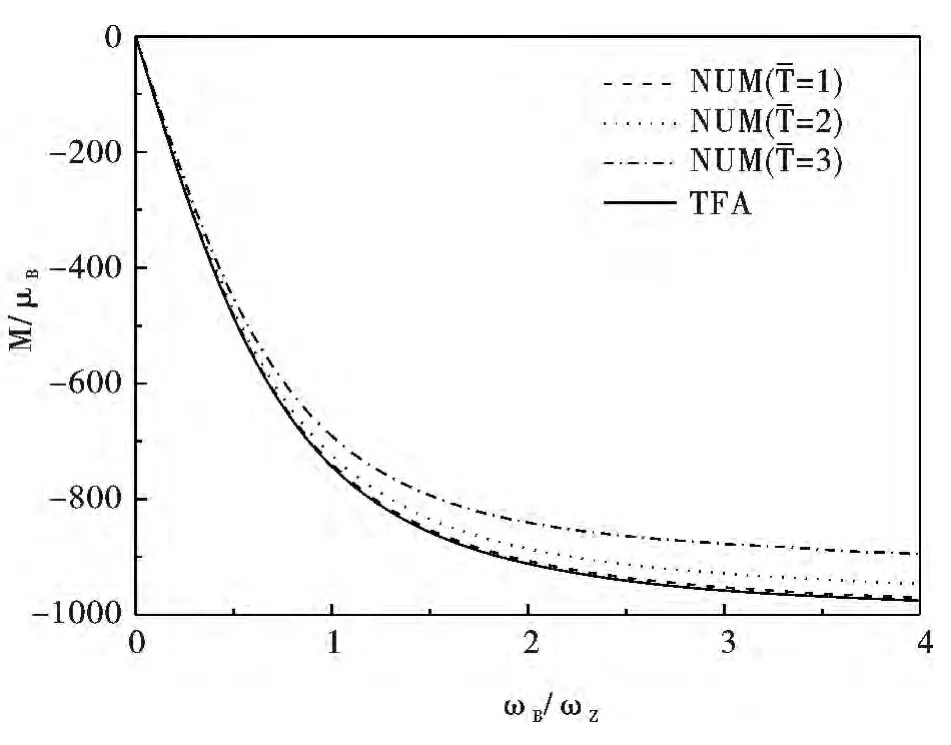
Fig.6 Magnetization versus magnetic field at various temperatures

Fig.7 Magnetization versus dimensionless temperature at various magnetic fields

Fig.8 Magnetic susceptibility versus temperature
4 Summaries
In conclusion,we have studied the thermodynamics of harmonically trapped Bose gases under a magnetic field utilizing numerical calculation.Through numerically calculating BEC temperature,internal energy,heat capacity and magnetization,we have observed some meaningful and remarkable findings.The numerical results show that the quantum effect and trapping effect are particularly important near BEC transition temperature. The diamagnetism is gradually strengthened along with the lower temperature and stronger magnetic field.
[1]Mav R M.Superconductivity of a charged ideal 2-dimensional Bose gas[J].Phys.Rev.,1959,254:115.
[2]Miller D E,Ray P S.Condensation of a charged relativistic Bose gas in the presence of a magnetic field[J].Phys.Rev.A,1986,33:1990.
[3]Ketterle W,van Druten N J.Bose-Einstein condensation of a finite number of particles trapped in one or three dimensions[J].Phys.Rev.A,1996,54:656.
[4]van Zyl B P,Hutchinson D A W.Charged two-dimensional quantum gas in a uniform magnetic field at finite temperature[J].Phys.Rev.B,2004,69:024520.
[5]Alexandrov A S.Normal-state diamagnetism of charged Bosons in cuprate superconductors [J].Phys.Rev.Lett.,2006,96:147003.
[6]Bagnato V,Pritchard D E,Kleppner D.Bose-Einstein condensation in an external potential [J].Phys.Rev.A,1987,35:4354.
[7]Bagnato V,Kleppner D.Bose-Einstein condensation in low-dimensional traps[J].Phys.Rev.A,1991,44:7439.
[8]Giorgini S,Pitaevskii L P,Stringari S.Condensate fraction and critical temperature of a trapped interacting Bose gas [J].Phys.Rev.A,1996,54:R4633.
[9]Baym G,Pethick C J.Ground-state properties of magnetically trapped Bose-condensed rubidium gas[J].Phys.Rev.Lett.,1996,76:6.
[10]Fan J H,Gu Q,Guo W.Thermodynamics of charged ideal Bose gases in a trap under a magnetic field[J].Chin.Phys.Lett.,2011,28:060306.
[11]Fetter A L.Rotating trapped Bose-Einstein condensates[J].Rev.Mod.Phys.,2009,81:647.
[12]Dalfovo F,Giorgini S,Pitaevskii P,etal.Theory of Bose-Einstein condensation in trapped gases[J].Rev.Mod.Phys.,1999,71:463.
[13]Yoshika D,F(xiàn)ukuyama H.Orbital magnetism of two-dimensional electrons in confining potentials[J].J.Phys.Soc.Jpn.,1992,61:2368-2381.
[14]Ishikawa Y,F(xiàn)ukuyama H.Orbital magnetism and current distribition of two-dimensional electrons under confining potential[J].J.Phys.Soc.Jpn.,1999,68:2405.
[15]Suzuki T,Imamura H,Hayashi M,etal.Orbital magnetism in three-dimensional quantum dots[J].J.Phys.Soc.Jpn.,2002,71:1242.
[16]Pethick C J,Smith H.Bose-Einstein condensation in dilute gases[M].Cambridge:Cambridge University press,2002(Print):16-37.
[17]Kling S,Pelster A.Thermodynamical properties of a rotating ideal Bose gas[J].Phys.Rev.A,2007,76:023609.
[18]Blindell S.Magnetism in condensed matter [M].Oxford:Oxford University press,2001:19-27.

