基于二維不可分小波變換的矩不變量

劉　斌　高　強（湖北大學計算機與信息工程學院武漢430062）

?

基于二維不可分小波變換的矩不變量

劉斌高強*
（湖北大學計算機與信息工程學院武漢430062）

尋找相對于尺度、平移、旋轉不變的小波不變量是多尺度分析在模式識別中應用的關鍵性問題。該文利用基于統計的不變矩這一理論和應用上都比較成熟的方法，將圖像有限個尺度的小波近似系數和圖像不變矩聯系起來，從而給出了一種小波矩不變量，得到了比較完善的理論和實驗結果。同時指出了該理論方法在實際應用中所需注意的地方，最后簡要闡述了多尺度分析與不變矩的應用關系。

模式識別；多尺度分析；2維不可分小波；不變矩；平滑性；近似系數

1　引言

在信號及圖像處理中，多尺度分析的思想由來已久，文獻［1］提出了基于LAPALACE金字塔式的分解從而進行多尺度的特征提取與識別，但金字塔分解后各層數據的相關性影響了它的性能。隨著小波理論［2］的發展，文獻［2］基于小波的塔式分解算法使各層的細節相對獨立而具有良好的應用。由小波及其多分辨率分析理論［3，4］可知，一幅圖像可分解為按尺度分辨率逐級降低的近似信息和細節信息，各個尺度的細節信息表示它不同的物理結構，而近似信息表示其總體輪廓，基于此理論上我們可從大尺度上分析圖像然后逐層細化識別，即所謂多尺度識別。多尺度識別的關鍵是找到待識別模式在有限個尺度下相對于平移、尺度、旋轉變化的不變量，這正是不變矩所具備的特性，據此可利用不變矩理論表征這種不變量。

不變矩理論從1維到多維都有比較成熟的理論和方法，可從目標圖像中提取不變矩作為特征進行目標的正確識別和圖像匹配等方面的應用［5］。文獻［6］利用代數不變量理論首次給出了2維不變矩的表示，其中階數小于3的7個具有平移、旋轉和尺度不變性的不變矩是應用的基礎。矩（中心矩）實際上反映物體灰度相對于質心的統計分布情況，計算量大而且高階矩受噪聲影響較大一直困擾著矩方法，這是矩對信號進行全局化處理造成的，為減小計算量人們也提出了一些改善的方法［7］。另一方面，圖像上物體可由各個不同相關聯的結構組成，而圖像的灰度信息只在各結構之間局部地相關著，而與其較遠的結構關系不大，就單個圖像像素而言它也只與附近一定范圍內的像素具有較強相關性，而與其距離越遠的像素越無相關性以至于幾乎不相關。受Fourier變換局部化的啟示，希望能將反映相關信息的矩方法也分層局部化，具有“數學顯微鏡”之稱的局部化分析工具小波是一種理想的選擇。

在Fourier分析的基礎上發展起來的小波分析在1維及其張量積形式情形下都有比較成熟的理論和方法，但利用張量積小波對2維圖像及更高維信號進行處理，由于其人為的方向性的處理方式顯然具有很大的缺陷。由此產生了2維非張量積的小波理論，并已有一些相關的理論和應用研究［810］-，但其總體的理論和應用遠不及1維小波那樣成熟。文獻［11］闡明了1維及2維張量積的小波矩不變量。本文在現有2維非張量積（不可分）小波理論的基礎上，結合不變矩的理論和方法從理論上進行推廣和拓展得到了在2維不可分情形下的小波矩不變量。同時進行了相應的數值驗證工作。此矩不變量比基于原圖像的矩值計算量大幅減小，同時繼承了不可分小波變換和不變矩的一些優點而使其能夠更好地應用于模式識別領域。

2　　2維不可分小波變換及其多分辨率分析理論

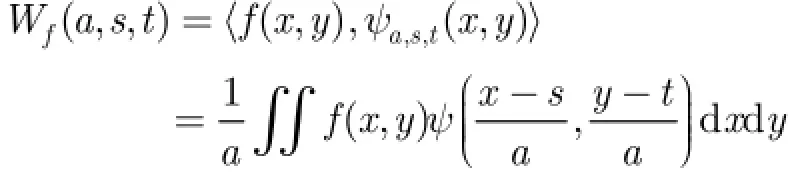
2維不可分的多分辨率分析可從相應的1維的多分辨率分析作推廣而得，具體是指在中有一串嵌套的閉子空間逼近序列滿足下列條件：

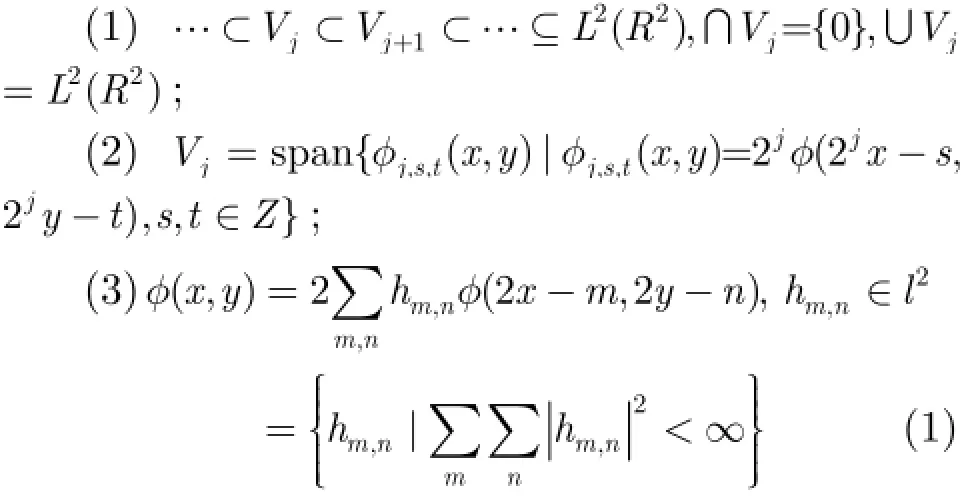
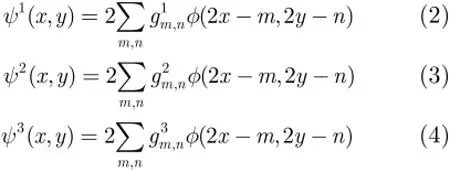
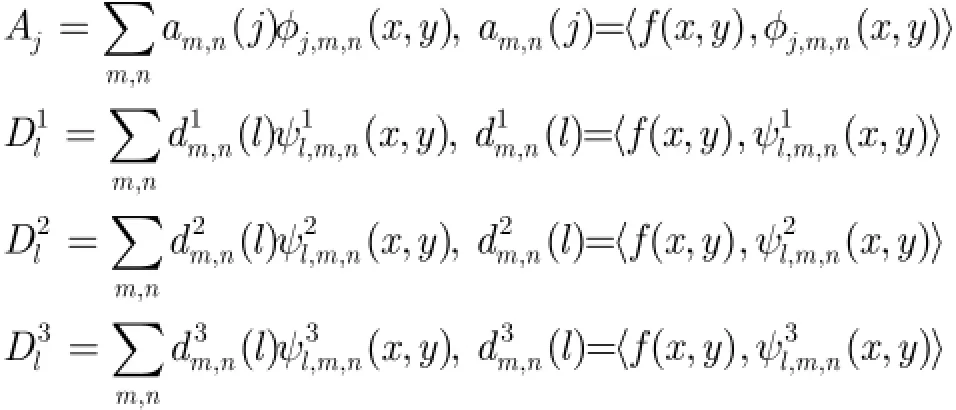
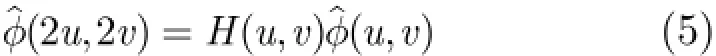
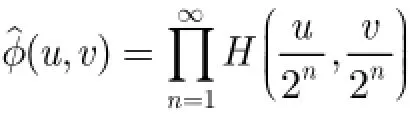
同理分別對式（2）、式（3）、式（4）兩邊作Fourier變換，可得

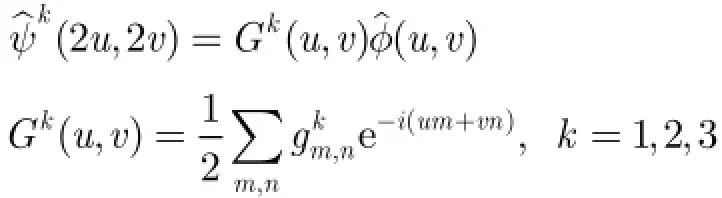
由以上分析可知（，）H u v的構造是多分辨率分析的關鍵，給定共軛濾波器（，）H u v滿足：

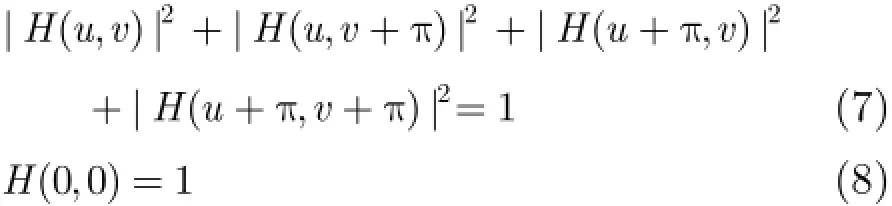
實際設計濾波器時都對（，）H u v有平滑性的要求，設（，）H u v可被分解為［14］

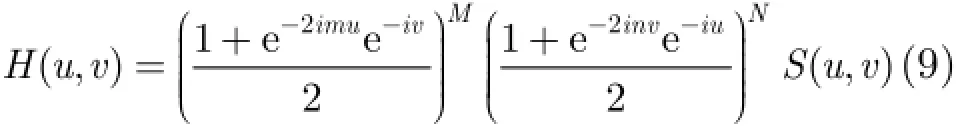
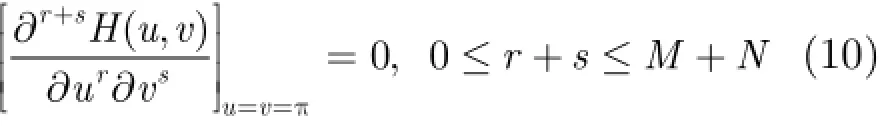
證明由2維小波分析理論，（1）中的等式顯然是成立的，以下簡要證明（2）中結論。

3　矩與小波不變矩

2維平面上灰度圖像（，）f x y的p q+階幾何矩［6］的定義為

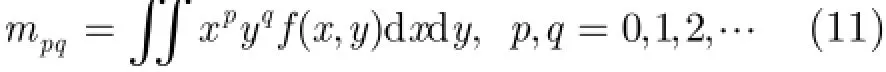
當（，）f x y在-x y平面上的有限區域內非零且分段連續時，pqm與（，）f x y互相唯一確定。矩的特定代數式在圖像平移、旋轉、尺度變化時保持定值，稱為不變矩。把坐標原點移至（，）f x y的質心，再除以一個尺度因子，可得到p q+階中心化規格矩：

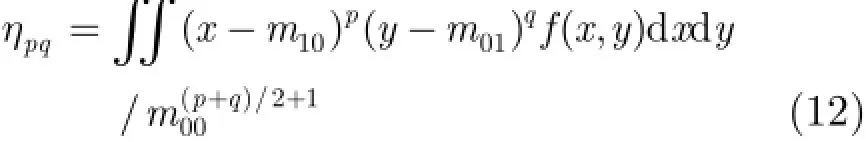
而由中心化規格矩可以組合表示出文獻［6］中的7個具有平移、旋轉、尺度變化的不變矩，這里不再列出。在文獻［6］工作的基礎上，文獻［15］進一步給出了離散情況下各階矩的計算方法，另外為保證離散情況下不變矩的尺度不變性，文獻［16］對歸一化的中心距進行了修正，實際情況下可借鑒這些方法以取得更好的應用效果。對函數（，）f x y作2維Fou rier變換可得（，）F u v對等式兩邊同時對u求 p階偏導，再接著對v求q階偏導，最后令有

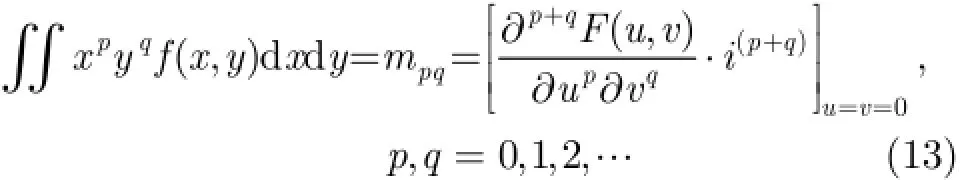
由式（13）和引理1可得引理2。

引理2如果（，）H u v在（0，0）點有M N+次平滑性，則

（1其下同；

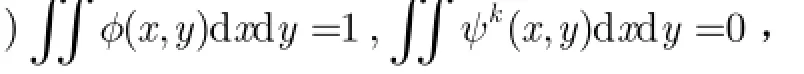
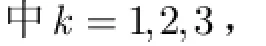
（2）

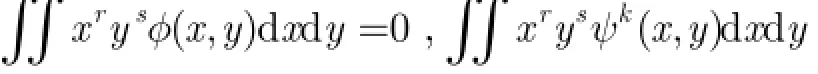
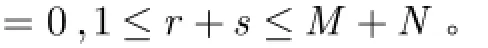
定理1如果共軛濾波器（，）H u v在（0，0）點有M N+次平滑性，將（，）f x y按（，）H u v構造的尺度函數及小波函數作小波展開，是其近似系數，令表示基于2維不可分小波變換近似系數的p q+階小波矩，則

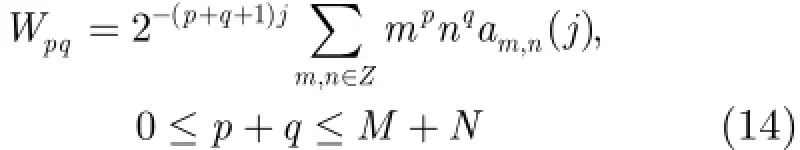
在設計共扼濾波器（，）H u v時，如果使（，）H u v在零點有M N+次平滑性，那么按照（，）H u v得到的尺度函數和小波函數將2維圖像（，）f x y在其上分解后產生的任一層次j的近似系數，理論上可無誤差地表達階次不大于M N+的矩值，式（14）中不出現細節系數。這表明圖像作2維不可分小波分解后，它的有限個視覺不變量將始終保留在任一層次的近似中而與任一層的細節無關，即得到了基于近似系數的小波矩不變量。這種基于近似系數的小波矩不變量，通過作平移、規格化及類似7個幾何不變矩的代數組合變換，就可得到基于近似系數的小波不變矩。這樣的小波不變矩有3個基本優點：其一，由于近似系數只為原始圖像數據量的1/4甚至更小（分解尺度增加時），故基于小波分解近似系數的矩值計算復雜性將大幅減小；其二，如果原始圖像存在噪聲，對圖像進行2維不可分小波分解后噪聲主要存在于細節系數中，這樣基于少量噪聲的近似系數計算得到的矩值比通過原始噪聲圖像計算的矩值應更準確和更能表征物體的特征，而有利于模式的正確識別；其三，小波變換可以獲取圖像中物體的細節結構特征，而在模式識別的理論和方法中，基于統計的不變矩能很好地對模式的特征信息進行描述［17］，故將小波變換和不變矩方法結合起來可充分利用兩者的優點，為進一步提出相關高效的模式識別應用算法奠定了基礎［18］。

實際應用中逼近層j和平滑性M+N的值是有限制的，盡管從原則上增大逼近層j和平滑性M+N能以較小的計算代價獲得更多的矩不變量信息，但在實際應用中將受到物體大小和Gibbs效應的影響。總地來說，為保證足夠的計算精度以利于精確識別，逼近層j應滿足為圖像尺寸，對此文獻［6］有較為詳細的分析；另一方面，圖像小波分解過程中的卷積會存在破壞邊界的Gibbs效應，這將影響待識別物體從背景的分割，而分割的好壞直接影響矩不變量的計算。為減少Gibbs效應的影響，M+N值也不能太大。

4　實驗與結果分析

本文利用設計得到的2維不可分小波濾波器在Matlab8.0平臺上對Lena灰度圖像進行分解后，計算其基于近似系數的矩不變量，結果列于表1。

理論上說階數小于5的矩值在任一層得小波逼近系數中應保持定值，而且階數越小其誤差值越小，實驗結果很好地反映了這一點。當然，隨著矩階數的增高和逼近層數的加大，誤差也逐漸增大，這是物體尺寸和Gibbs效應的影響，已在第3節中指出。

為驗證式（14）的抗噪性能，本文對Lena圖像加噪聲（見圖1）后同樣利用2維不可分濾波器對噪聲圖像進行分解求其不同尺度下的矩不變量，將其與按式（11）計算得到的無噪聲圖像原始準確矩值比較，得出表2數據。

由表2的矩值誤差數據明顯可知第0層的矩值誤差是最大的，而隨著分解層數的增加近似系數受噪聲影響越來越小使其矩值誤差相對準確值的誤差越來越小，正如第3節所述這是由于小波變換將原圖像的大部分噪聲分解到細節系數中，而近似系數所含噪聲較少的緣故。當然隨著尺度的進一步增大，由于物體尺寸和Gibbs效應及其他原因導致的誤差增加導致相對準確矩值的誤差值有所變大，但總體成減小的趨勢。

表1　基于分解近似系數的圖像矩值及其誤差值

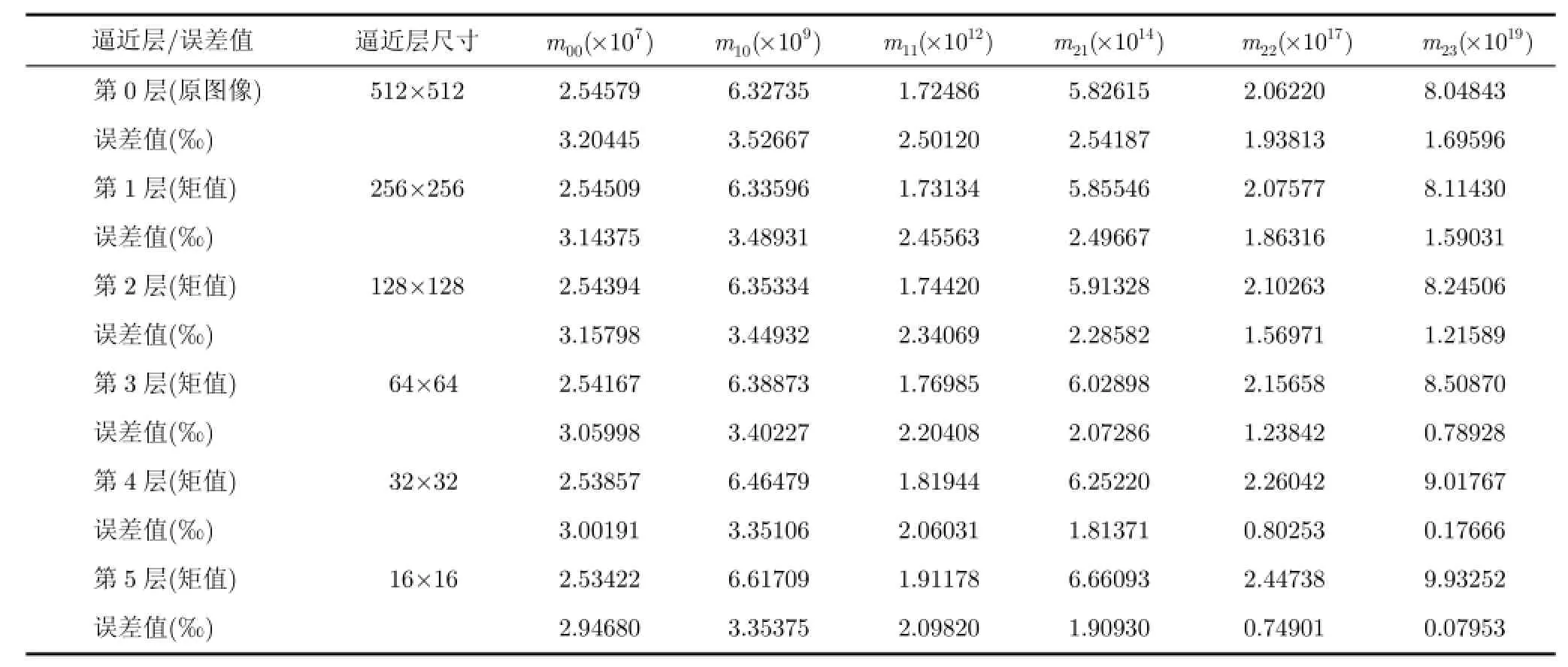
表2　基于分解近似系數的加噪圖像矩值及其對比誤差值

圖1　原始Lena圖像和加噪Lena圖像

就式（14）的計算復雜度而言，由理論推導可知近似系數只有原始圖像數據量的1/4。假設離散的原圖像尺寸為N N×，一般幾何矩是按式（11）對原始圖像進行處理，其計算復雜度為而本文是對只有原始圖像尺寸1/4的近似系數進行處理，原始數據量的減小顯然將大幅降低計算量。假如式（14）的計算是基于第1層的近似系數，則其計算復雜度將降低為而如果其基于更大尺度（層數）的近似系數即尺度的近似系數，計算復雜度將進一步降為這顯然在原始的計算復雜度基礎上大幅減小了（4S-1）/4S的計算量。

5　結束語

本文從理論上推導得到了基于矩的小波矩不變量（小波不變矩），并指出它在實際應用中的局限性和需要注意的地方。多尺度分析是通過減少信號不必要的細節在大尺度范圍內進行識別，而不變矩方法則要求盡可能多地保留物體的特征，特別是有助于區分近似物體的細節特征，這兩種方法之間有一種內在的矛盾性和互補性。通常在模式識別中，需從總體輪廓上把握物體的特征，這樣的識別方法具有抗噪性和抗干擾性［19］，而保留物體的細節特征有助于區分形近的物體但卻導致對噪聲和干擾的敏感。于是為了消除細節減少數據量，必須增大尺度，但這樣做同時會使不變量數值不精確和導致表征細節特征信息不充分；另一方面，為盡可能準確地計算不變量必須盡量保持數據，從而要求逼近尺度不能太大。實際應用中兩種方法的有機結合是很必要的，最合理的妥協就是每個物體在其合適的層次得到識別。

［1］李駿揚，金立左，費樹岷，等.基于多尺度特征表示的城市道路檢測［J］.電子與信息學報，2014，36（11）:2578-2585.doi: 10.3724/SP.J.1146.2014.00271.

LI Junyang，JIN Lizuo，FEI Shum in，et al.Urban road detection based on multi-scale feature representation［J］. Journal of Electronics&Information Technology，2014，36（11）:2578-2585.doi:10.3724/SP.J.1146.2014.00271.

［2］MALLAT S G.A Theory for multi-resolution signal decom position:the wavelet representation［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，1989，1（7）:674-693.

［3］MALLAT SG.Multiresolution approximations and wavelet orthonormal bases of L2（R）［J］.Transactions of the American Mathematical Society，1989，315（1）:69-87.

［4］DAUBECHIES I.Orthonormalbasesof com pactly supported wavelets［J］.Communications on Pure And Applied Mathematics，1988，41（7）:909-996.

［5］PRASHAN P and MALIN P.Imagematching usingmoment invariants［J］.Neurocomputing，2014，137:65-70.doi: 10.1016/j.neucom.2013.02.058.

［6］HU M K.Visualpattern recognition by moment invariants［J］. IEEE Transactions on Information Theory，1962，8（2）: 179-182.

［7］謝生龍，王夏黎，董春雨，等.基于不變矩理論線矩法圖像特征的提取［J］.計算機技術與發展，2014，24（11）:139-143.doi: 10.3969/j.issn.1673-629X.2014.11.035.

XIE Shenglong，WANG Xiali，DONG Chunyu，et al. Extraction of figure featuresbased on linemomentmethod of moment invariant theory［J］.Computer Technology and Developm ent，2014，24（11）:139-143.doi:10.3969/j.issn.1673-629X.2014.11.035.

［8］軒建平，鄭鋒.基于Coiflet的二維小波有限元構造與應用［J］.華中科技大學學報（自然科學版），2014，42（5）:21-24.doi: 10.13245/j.hust.140505.

XUAN Jianping and ZHENG Feng.Construction and application of two-dimentional wavelet finite element based on Coiflet［J］.Huazhong University of Science&Technology，2014，42（5）:21-24.doi:10.13245/j.hust.140505.

［9］HUR Y，PARK H，and ZHENG Fang.M ulti-D wavelet filter bank design using quillen-suslin theorem for laurent polynom ials［J］.IEEE Transactions on Signal Processing，2014，62（20）:5348-5358.doi:10.1109/TSP.2014.2347263.

［10］HUAE Y.Construction of com pactly supported nonseparable orthogonal wavelet w ith dilation 4［J］.Advanced M aterials Research，2014，1061（1）:1064-1069.

［11］金琪，戴汝為.基于矩表示的小波不變量［J］.模式識別與人工智能，1995，8（3）:179-187.

JIN Qiand DAIRuwei.Wavelet invariants based onmoment presentation［J］.Pattern Recognition and Artificial Intelligence，1995，8（3）:179-187.

［12］AYACHE A.Som e m ethods for constructing non-separable，orthonormal，com pactly supported wavelet bases［J］.Letter to the Editor In Applied And ComputationalHarmonic Analysis，2001，10（1）:99-111.

［13］DAUBECHIES I.Ten Lectures on Wavelets［M］.Vermont: Capital City Press，1992:299-300.

［14］徐應祥，關履泰.具有消失矩的新二元正交小波［J］.云南大學學報（自然科學版），2010，32（4）:385-391.

XU Yingxiang and GUAN Lütai.New bivariate orthogonal wavelets w ith vanishing moments［J］.Journal of Yunnan University，2010，32（4）:385-391.

［15］WONG Y R.Scene m atching w ith invariant m om ents［J］. Computer Graphics and Image Processing，1978，8（1）:16-24.

［16］潘泉，程詠梅，杜亞娟，等.離散不變矩算法及其在目標識別中的應用［J］.電子與信息學報，2001，23（1）:30-36.

PAN Quan，CHENG Yongmei，DU Yajuan，et al.Discrete moment invariant algorithm and its application on target recognition［J］.Journal of Electronics&Information Technology，2001，23（1）:30-36.

［17］沈會良，李志能.基于矩和小波變換的數字、字母字符識別研究［J］.中國圖象圖形學報，2000，5A（3）:249-252.doi:10.3969 /j.issn.1006-8961.2000.03.015.

SHEN Huiliang and LIZhineng.A study ofnumber and letter character recognition based on m om ents and wavelet transform［J］.Journal of Image and Graphics，2000，5A（3）: 249-252.doi:10.3969/j.issn.1006-8961.2000.03.015.

［18］毛賢光，李云欣，李罕，等.基于不變矩和小波分析的指橫紋匹配新算法［J］.計算機工程與應用，2015，51（20）:172-177. doi:10.3778/j.issn.1002-8331.1310-0109.

MAO X ianguang，LI Yunxin，LI Han，et al.New m atching algorithm of knuck leprint based on m om en t invariants and wavelet mu lti-resolution analysis［J］.Computer Engineering and Applications，2015，51（20）:172-177.doi:10.3778/j.issn. 1002-8331.1310-0109.

［19］丁曉青.漢字識別研究的回顧［J］.電子學報，2002，9（9）: 1364-1368.doi:10.3321/j.issn:0372-2112.2002.09.029.

DING Xiaoqing.Chinese character recognition:a review［J］. Acta Electronica Sinica，2002，9（9）:1364-1368.doi:10.3321/ j.issn:0372-2112.2002.09.029.

劉斌：男，1963年生，教授，博士生導師，主要從事模式識別、圖像處理及小波理論的研究.

高強：男，1988年生，碩士生，研究方向為圖像處理、模式識別.

Moment Invariants Based on Two Dimensional Non-separable Wavelet Transform

LIU Bin GAO Qiang
（School ofComputer and Information Engineering，Hubei University，Wuhan 430062，China）

Searching for wavelet invariants is a key issue in m ultiresolu tion analysis.On the other hand，them ethod ofmoment invariants is fully developed both in the theory and the p ractice.A kind ofwaveletmoment invariants are given based on the image invariantmoments and wavelet app r-oximation coefficients from the lim ited number of scales of the image.A fairy com plete result on theory and experiment is obtained.At the same time，some problem sof the theory and method are pointed out in the p racticalapplication.Finally，the application relationship betweenmu lti-scale analysis and invariantmoment is briefly described.

Pattern recognition；M ulti-scale analysis；Two dim ensional non-separable wavelet；Invariantm om ent；Smoothness；App roximation coefficients

s:The National Natural Science Foundation of China（61471160），The Key P roject of the Natural Science of Hubei Province（2012FFA 053）

TP391.41

A

1009-5896（2016）08-2085-06

10.11999/JEIT 151218

2015-11-03；改回日期：2016-05-03；網絡出版：2016-06-12

高強shengqiang8814@qq.com

國家自然科學基金（61471160），湖北省自然科學基金（2012FFA 053）