基于體積力法的全附體KCS型船模PMM運動數值模擬

王慧婷，畢毅

海軍工程大學艦船工程系，湖北武漢430033

基于體積力法的全附體KCS型船模PMM運動數值模擬

王慧婷，畢毅

海軍工程大學艦船工程系，湖北武漢430033

為高效、精確地求解船舶操縱水動力導數，以全附體KCS型船模為研究對象，基于RANS方程及VOF模型，在star-ccm+平臺上采用體積力法模擬螺旋槳作用，計及自由面興波及航行姿態變化對船模水動力的影響，開展斜航、純艏搖、漂角和艏搖組合3種平面運動機構（Planar Motion Mechanism，PMM）運動的數值模擬，將橫向力Y、艏搖力矩N、橫傾力矩K的數值模擬結果與試驗結果進行對比，并依照PMM試驗的動力學方程，通過最小二乘法擬合和傅立葉積分，將數值模擬結果與試驗結果的時歷曲線進行分析處理，求得操縱水動力導數。研究結果表明：該方法用于數值模擬PMM運動是可行的；求得的水動力導數中Y′vvv，N′vvv誤差略大，其余水動力導數誤差均在15%以內。

體積力法；KCS船型；平面運動機構；水動力導數

網絡出版地址：http://www.cnki.net/kcms/detail/42.1755.TJ.20160729.0945.010.html期刊網址：www.ship-research.com

引用格式：王慧婷，畢毅.基于體積力法的全附體KCS型船模PMM運動數值模擬［J］.中國艦船研究，2016，11（4）：29-37，66.

WANG Huiting，BI Yi.Numerical simulation on planar motion mechanism of KCS ship model with a body-force propeller mode［lJ］.Chinese Journal of Ship Research，2016，11（4）：29-37，66.

0　引　言

操縱性是船舶重要的航行性能，在船舶設計階段需對操縱性進行預報。隨著計算機及CFD技術的快速發展，采用計算機數值模擬方法預報船舶操縱性能已成為一種技術方法，而數值預報的關鍵是確定船舶操縱運動方程中的水動力導數。目前常用的有拘束模試驗和數值計算2種方法，其中拘束模試驗精度較高，但試驗過程繁雜，需耗費大量的人力、物力，而數值計算則具有很多優點，如計算效率高、可以獲得流場細節等，目前已獲得較快的發展。

針對水動力導數的數值求解，最為常用的是數值模擬船舶平面運動機構（Planar Motion Mechanism，PMM），通過對計算中的時歷曲線進行分析得到。目前，國內外學者對這方面均做了一定的研究。Broglia等［1］對KVLCC2船模進行了考慮自由面影響的純橫蕩運動模擬，同時，Broglia等［2］數值模擬了帶槳、舵的KVLCC1&2船的純橫蕩和純艏搖運動；Tyagi和Sen［3］利用RANS方程對2種典型AUV的斜拖運動進行了研究；Sakamoto等［4］和Guilmineau等［5］對光體DTMB 5415船模進行了PMM運動模擬；Miller［6］對光體和全附體的DTMB 5415船模均進行了PMM運動數值模擬，結果表明全附體所得結果誤差較小。國內學者劉山［7］和程捷等［8］以光體DTMB 5415船模為研究對象，模擬了純橫蕩和純艏搖運動，并求得了相應的水動力導數；楊路春等［9］模擬了SUBOFF主艇體的平面運動，并求解了水動力導數；樓鵬宇［10］和石愛國等［11］均對限制水域中船舶的PMM運動進行了數值模擬。

然而，上述研究中均沒有真實地模擬船模PMM的試驗，有些未考慮自由面及運動過程中船模姿態變化的影響，有些未考慮附體的影響而只對光體船模進行了計算。即便考慮了槳、舵，因螺旋槳采用的是實體建模的方法，計算工作量較大，周期較長。體積力法［12-13］的計算效率較高，能反映螺旋槳作用，可以預報流場信息，但目前將該方法應用于船模PMM運動數值模擬的研究還較少。

針對以上研究現狀，本文將基于star-ccm+平臺，采用體積力法，對全附體KCS型船模進行斜航、純艏搖、漂角和艏搖組合這3種PMM運動數值模擬，并考慮自由液面興波和航行姿態變化的影響，測得船模運動中所受的橫向力、艏搖力矩及橫傾力矩，將計算結果與試驗結果進行對比分析，以獲得相應的水動力導數。

1　數值計算模型

1.1控制方程

對于雷諾平均后的不可壓縮粘性流問題，采用的連續性方程和動量方程如下：

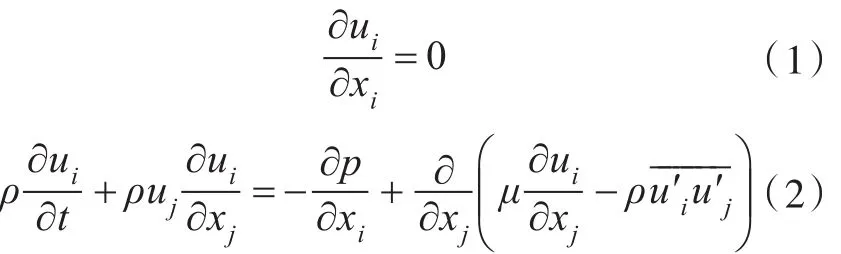
式中：ui為平均速度分量；p為平均壓力；ρ為流體質量密度；μ為流體分子粘性系數；為

雷諾應力項。式（2）即為雷諾平均Navier-Stokes （Reynolds Averaged Navier-Stokes，RANS）方程。

1.2湍流模型

當求解分離和帶有復雜二次流特征的流動時，Realizable k-ε模型優于標準k-ε模型，因此，采用Realizable k-ε湍流模型來封閉RANS方程。

Realizable k-ε湍流模型輸運方程為：

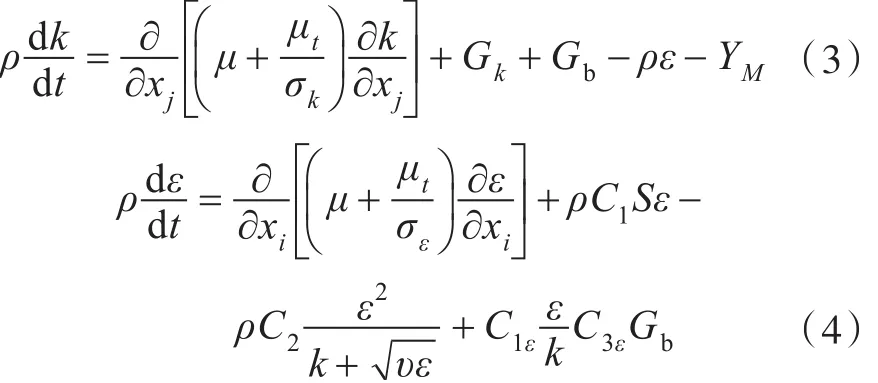
1.3體積力源項方程

采用基于勢流升力面理論的渦格法，產生符合槳葉邊界條件的體積力，將其作用在螺旋槳區域網格上，施加推力和扭矩以代替真實的螺旋槳表面載荷。相關公式如下：

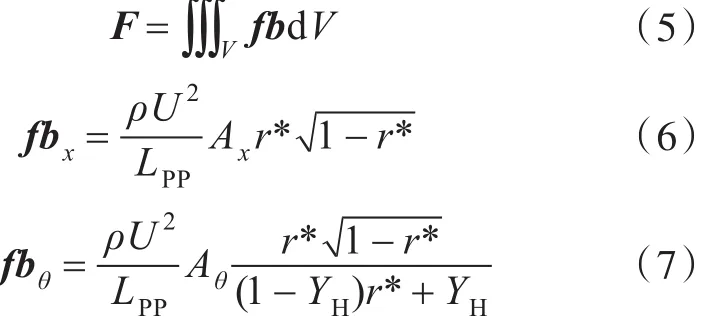
其中：

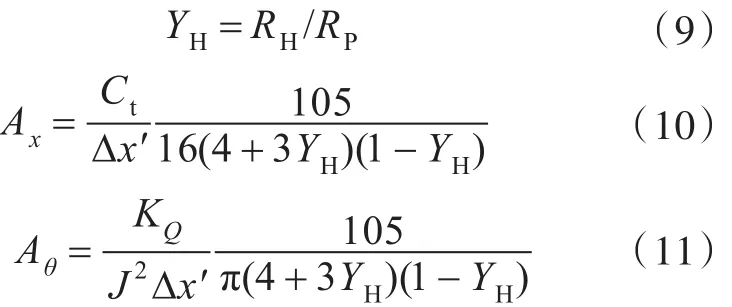
式中：Ct=2T/（ρU2πRp），為一種無量綱推力系數；KQ=Q/ρn2DP5，為轉矩系數，其中n為螺旋槳轉速；DP=2RP，為螺旋槳直徑；r1為螺旋槳區域內任意一點到螺旋槳軸線的距離；RP和RH分別為螺旋槳半徑和槳轂半徑；LPP為船體垂線間長；Δx′=Δx/LPP，為槳轂厚度與船體垂線間長之比；J=Va/nDP，為螺旋槳進速系數，其中Va表示螺旋槳進速。

螺旋槳采用體積力法，即運用描述型體積力模型代替真實螺旋槳作用，此時，體積力模型中螺旋槳的作用區域如圖1所示。 Kt，KQ取自Simman 2014中KCS船螺旋槳敞水試驗結果。螺旋槳轉速n與試驗中相同，在star-ccm+軟件中計算螺旋槳推力T和轉矩Q時，需在螺旋槳作用區域前設定一虛擬的靜流盤面，該盤面上的平均速度作為用體積力法計算時的進流速度，船尾流場的不均勻性體現在虛擬盤面平均速度上。

圖1　螺旋槳作用區域Fig.1　The operational zone of propeller

2　計算對象及工況

2.1研究對象

本文以船舶操縱預報方法驗證與確認專題討論會Simman 2014中的基準算例作為參考，選取深水中帶全附體的KCS型船模為研究對象。模型縮尺比為52.667，主要參數見表1。

2.2PMM運動計算模型

對KCS型船模進行斜航、純艏搖、漂角和艏搖組合這3種PMM運動。船模運動方式定義如圖2所示。

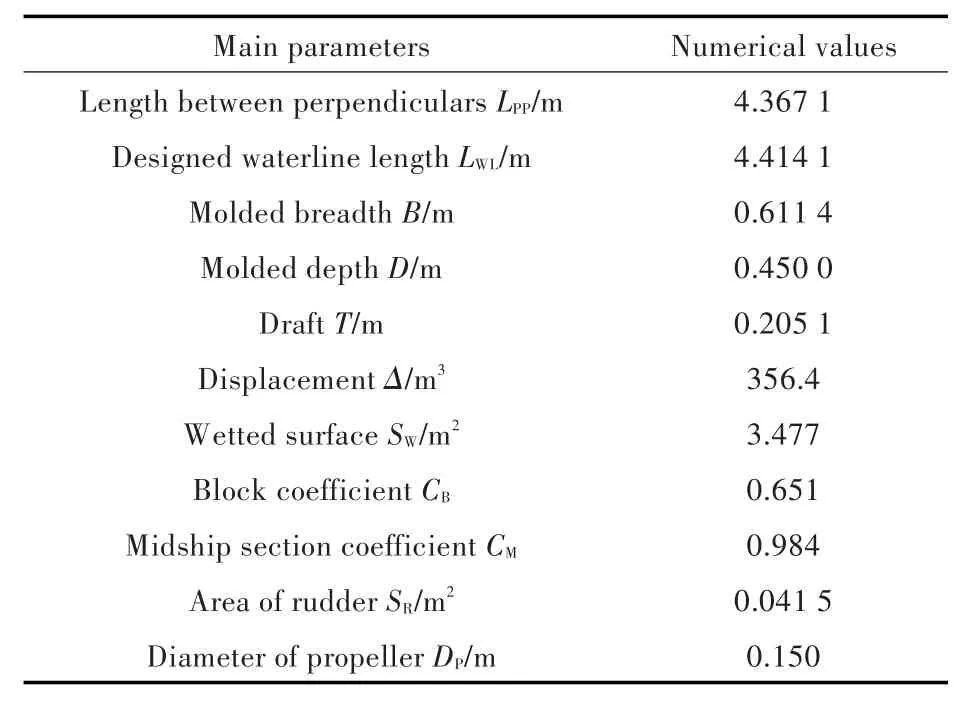
表1　KCS型船模主要參數Tab.1　Main parameters of the KCS model

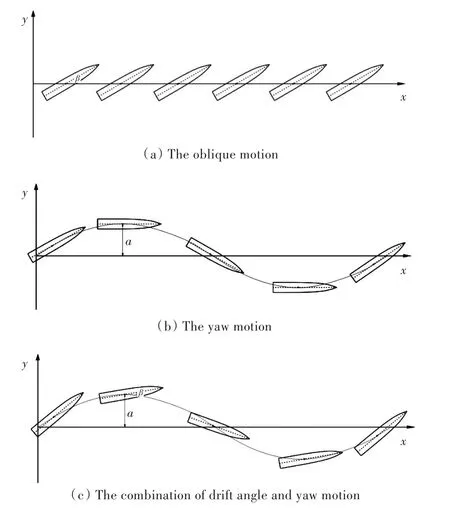
圖2　船模運動方式Fig.2　Motion mode of ship model

運動中，重點分析船模所受的橫向力Y，艏搖力矩N及橫傾力矩K，其無因次化形式為：

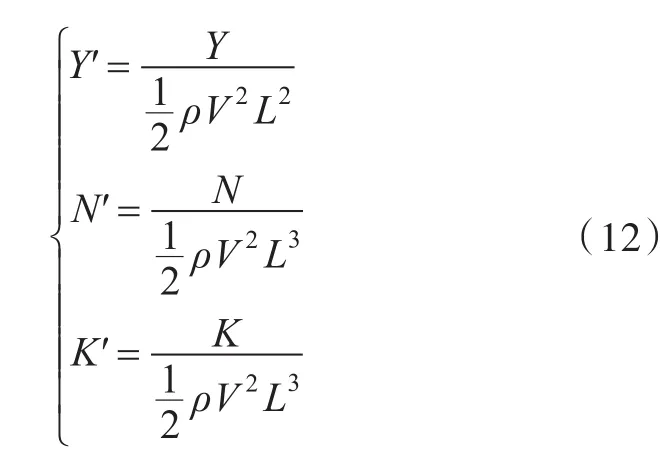
式中：V為航速；L為船長。

2.2.1斜航運動計算模型

斜航運動中，其運動表達示為

式中：r為角速度；v為橫向速度；β為漂角。

船模所受水動力可表達為

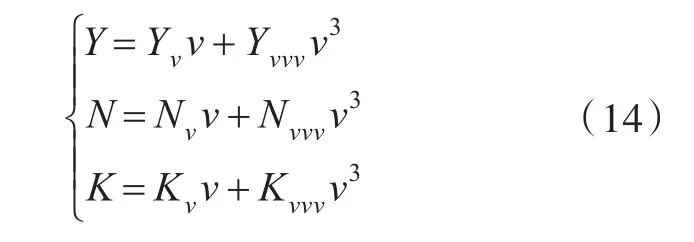
對計算所得的水動力進行無因次化，將無因次水動力隨無因次橫向速度v′的變化曲線采用最小二乘法進行擬合，即得Yv′，Yvvv′，Nv′，Nvvv′，Kv′，Kvvv′。

2.2.2純艏搖運動計算模型

純艏搖運動中，其運動表達示為

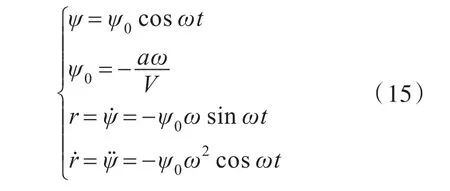
其中：a為幅值；ψ0為艏向角幅值；ψ為艏向角；ω為角頻率。

在船體坐標系下，水動力表達式為

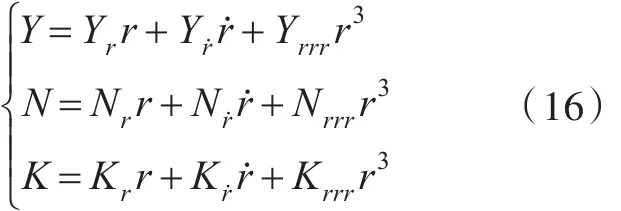
以橫向力Y為例，將運動表達式代入，其無量綱化形式為

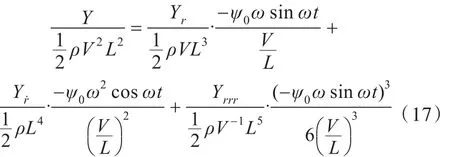
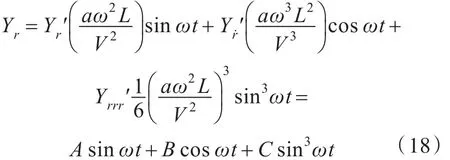
對船模運動中所受的無因次水動力曲線進行擬合得到各系數項A，C，再通過不同幅值a時的運動模擬結果對A和C進行二次擬合，直線斜率即為Yr′，Yrrr′。同理，可得Nr′，Nrrr′，Kr′，Krrr′。因此，對船模進行3個不同幅值下的純艏搖運動，以求得相應的水動力導數。

2.2.3漂角和艏搖組合運動計算模型

漂角和艏搖組合運動中，其運動表達式為

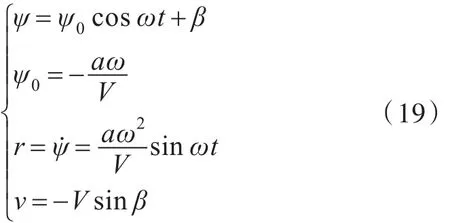
在船體坐標系下，水動力表達式為

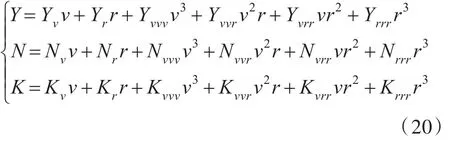
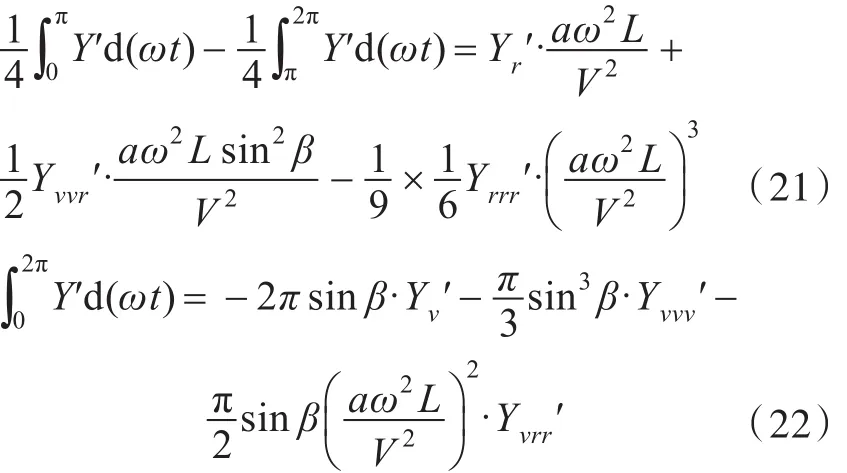
采用離散化函數積分形式計算式（21）和式（22）左邊的積分值，代入已求得的Yr′，Yrrr′，Yv′，Yvvv′中，即可得到和。同理，可得Nv′

vr，，，。因此，漂角和艏搖運動選取一個狀態下的運動即可求得相應的水動力導數。

2.3計算域及邊界條件

采用矩形計算域，斜航運動時，在入流面給定一垂直于入流面的來流，船模與來流方向成一定的角度保持不動，即采用相對運動的方式使船模實現指定漂角下的斜航運動；純艏搖、漂角和艏搖組合運動時，船模在水中做相應的運動。計算域的大小和入流面、出流面的位置由船長L確定，通常，須保證計算區域在船前不小于1倍船長，在船后和左、右兩側不小于2倍船長。如船模在深水中運動，下邊界距船模應不小于2倍船長，船模計算域如圖3所示。

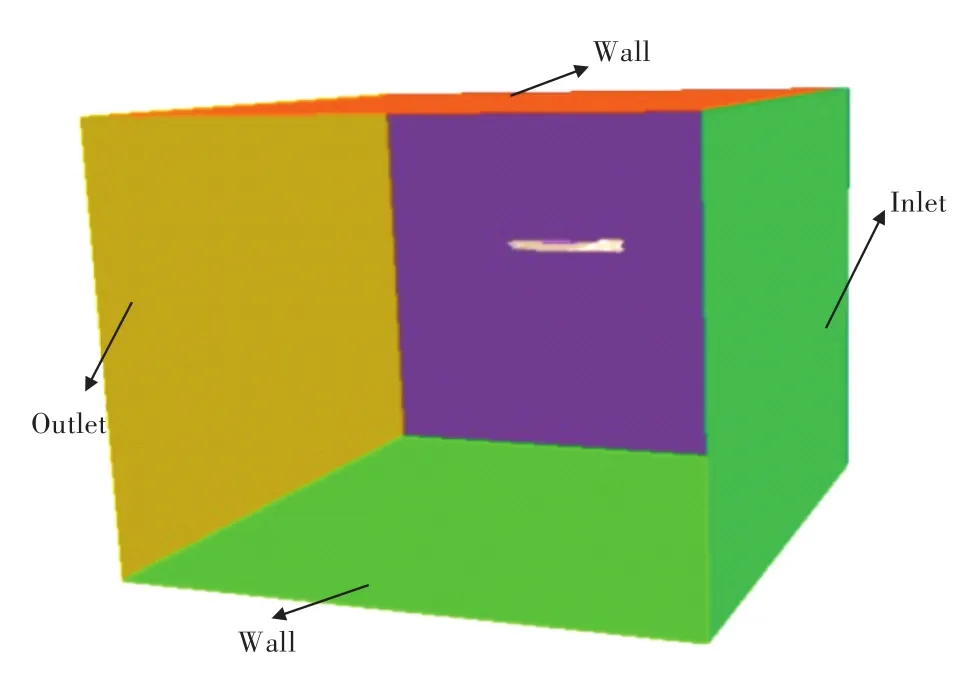
圖3　船模計算域Fig.3　Computational domain of ship model

邊界條件的設置如下：

1）入流面：速度入口，當船模做純艏搖、漂角和艏搖組合運動時，來流速度為0 m/s。

2）出流面：壓力出口，自由液面以上為標準大氣壓，以下設置為靜水壓力。

3）船模表面：無滑移壁面。

4）上、下、左、右外邊界：同入流面。

2.4網格劃分

數值模擬中所使用的網格均為全六面體非結構化網格，對運動產生的興波區域、自由面附近以及船首、尾部分進行加密。船模首、尾部網格劃分如圖4所示，計算域的網格劃分如圖5所示，斜航運動時將船模及周圍加密區網格旋轉相應的角度，形成對應的計算域網格。

圖4　船首、尾部網格劃分Fig.4　Grid partition on the bow and stern

圖5　計算域的網格劃分Fig.5　Grid partition on the computational domain

2.5網格密度的選取

為分析不同網格密度對計算結果的影響，以漂角β=-8°時的斜航運動為例，對4種不同網格密度下的計算域進行計算，并對結果進行對比分析。選取計算域x軸方向為（-1.5～2.5）L，y軸方向為（-2.5～2.5）L，z軸方向為（-2.0～1.0）L。固定邊界層的總厚度為0.02 m，通過改變層數來改變第1層網格到船體表面的距離，進而影響著網格密度，網格具體情況如表2所示。

由表2可知，隨著邊界層層數的增加，計算所得水動力趨于穩定。當邊界層層數為10層時，已在穩定范圍之內，因此，本文采用此網格密度下的計算域進行計算。

3　數值模擬結果及分析

為驗證所使用方法及計算結果的正確性，將結果與 Simman 2014中“KCS PMM tests with appended hull，FORCE 2009”試驗結果進行了對比。各PMM運動數值模擬計算工況如表3所示。

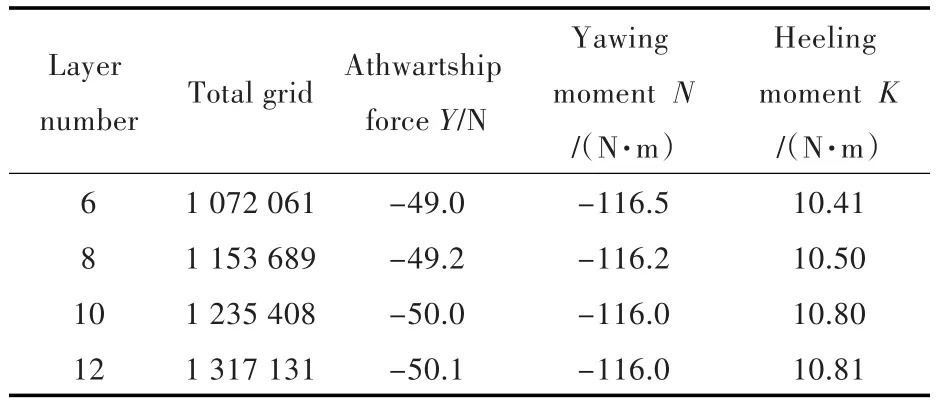
表2　不同網格數量下的水動力比較Tab.2　Comparison of hydrodynamics under different grid quantities

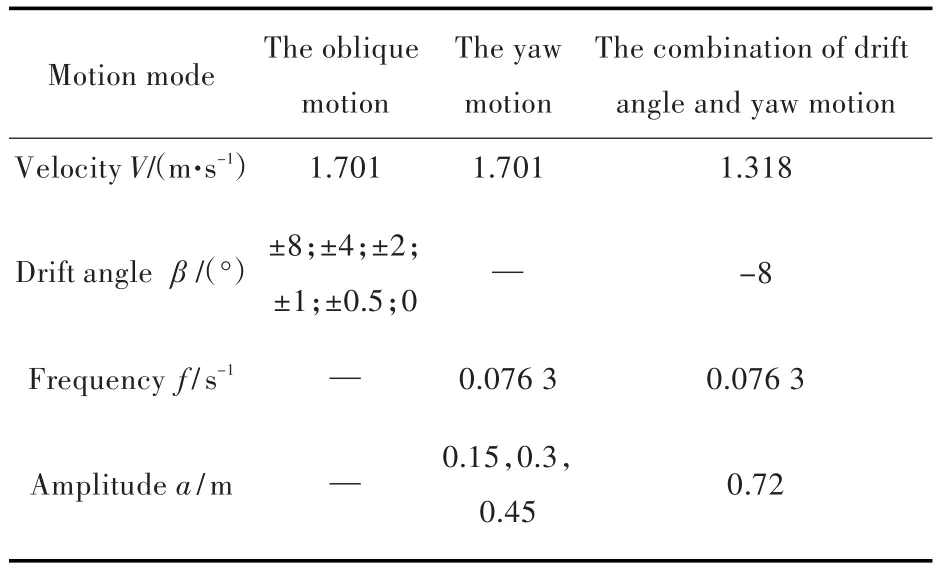
表3　各PMM運動數值模擬計算工況Tab.3　Calculation condition of planar motion's numerical simulation

3.1斜航運動計算結果

通過數值模擬，計算得到船模所受的無因次水動力隨漂角β的變化曲線如圖6所示。從圖中可以看出，各漂角下橫向力的計算結果與試驗結果吻合較好；對于艏搖力矩，計算結果與試驗結果有一定的誤差，因即使橫向力計算與試驗結果誤差很小，反映到艏搖力矩上誤差也會增大，因此圖中所示結果差距是可以接受的；而對于橫傾力矩，計算結果與試驗結果相差不大，且計算結果曲線與試驗結果曲線的變化趨勢非常相似。

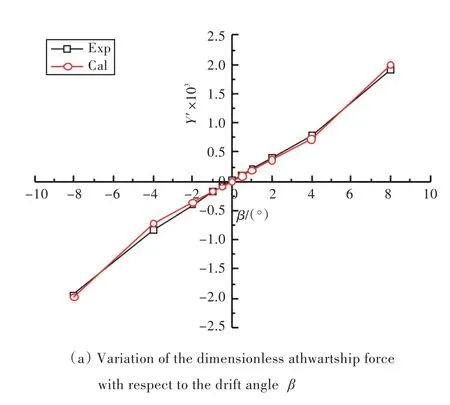
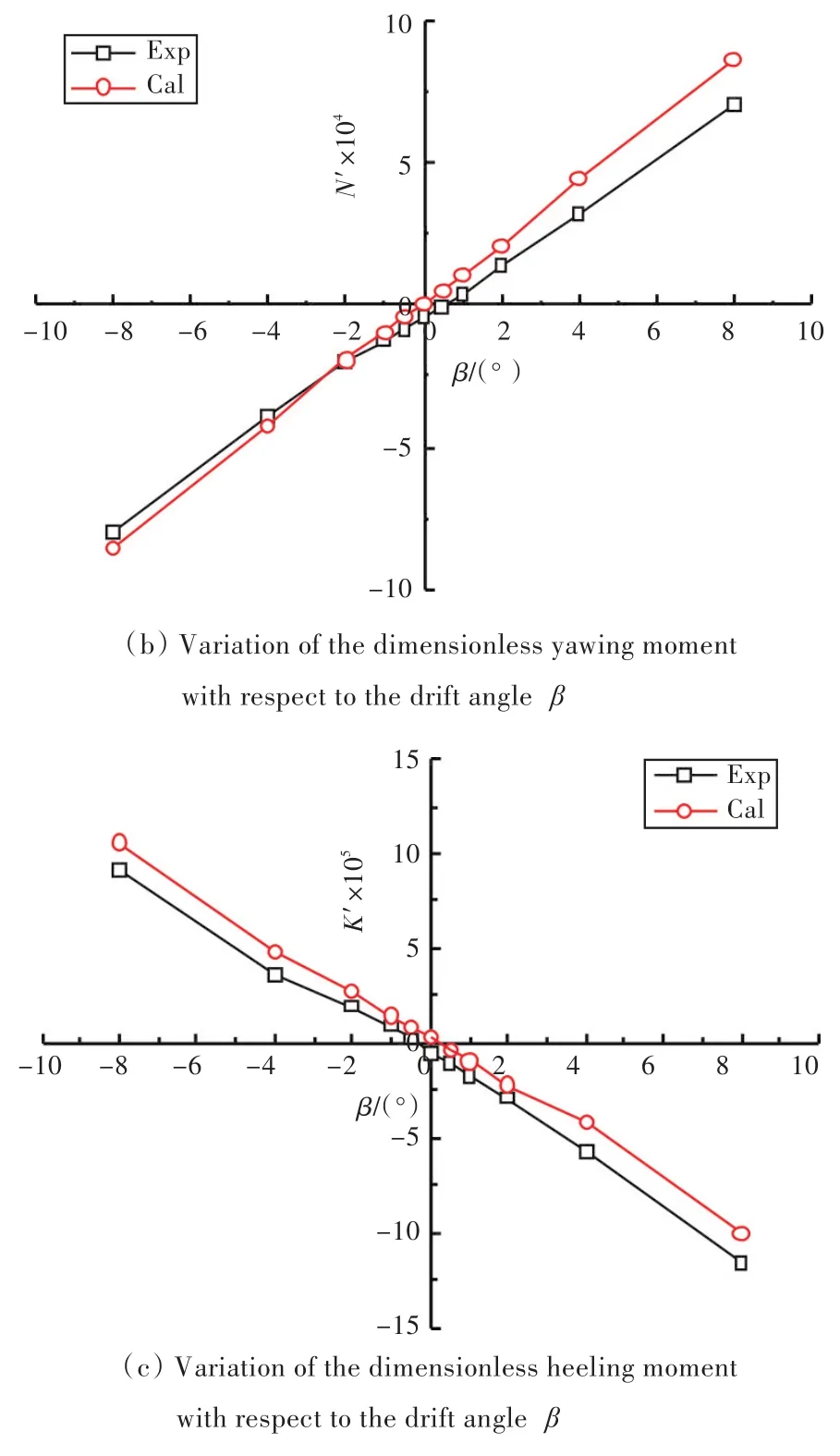
圖6　船模所受無因次水動力隨漂角β變化曲線Fig.6　Variation of the dimensionless hydrodynamics with respect to the drift angleβ

根據無因次水動力隨漂角 β變化的曲線，采用最小二乘法求得的水動力導數如表4所示。由表中可看到，高階導數的誤差略大，其余水動力導數誤差均在20%以內。

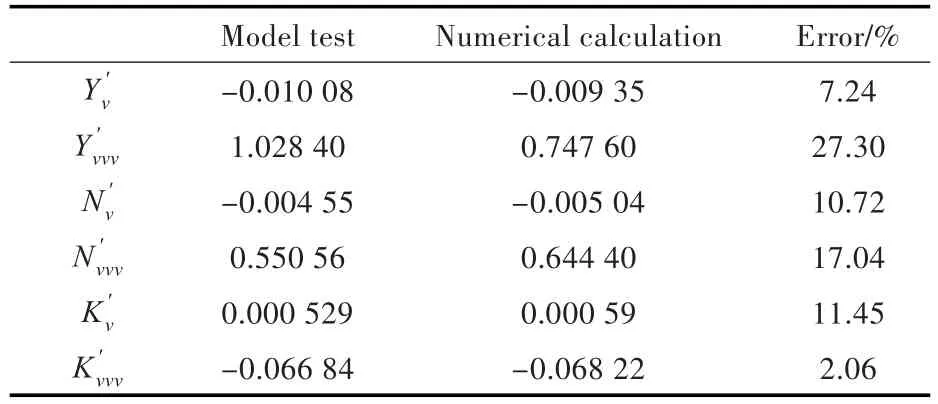
表4　斜航運動中水動力導數計算結果Tab.4　The calculation results of the hydrodynamic derivatives in the oblique motion

運動中，當漂角β為-2°和-4°時，船體周圍興波圖如圖7所示。由圖可知：隨著漂角的增加，船體兩側的興波越來越不對稱，背流面散出的波形距離船體越來越遠，較好地反映出運動中船體周圍波形的變化規律。

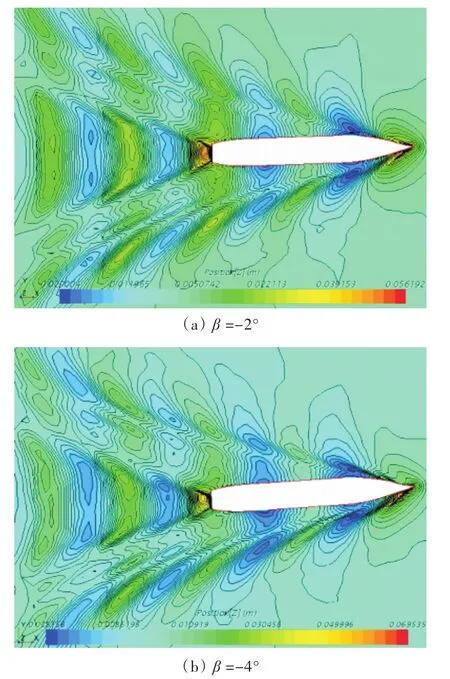
圖7　漂角為-2°和-4°時船體周圍興波圖Fig.7　The free surface wave patterns around the hull in the static drift atβ=-2°andβ=-4°

3.2純艏搖運動計算結果

當船模運動穩定后，選取一個周期內的數值模擬結果進行研究。振幅為0.15，0.3，0.45 m時船模所受的無因次水動力時歷曲線分別如圖8～圖10所示。分析可得，船體做簡諧運動時，所受的力與力矩均應符合簡諧規律。由圖可知，計算結果較好地體現出了簡諧規律，而試驗結果則存在著一定的波動，這有可能來源于試驗中測量力裝置的量程、安裝方式及數據處理方法等，且K/N≈0.05，橫傾力矩較小，試驗不易測得。橫向力、艏搖力矩的試驗與計算結果吻合良好，而橫傾力矩的則略有誤差，這是因為數值計算中采用RANS控制方程對平均時間內的壓力和速度進行描述，不能較為精細地捕捉到船體周圍的渦產生及脫落等非定常現象，會對計算結果帶來一定的影響。橫向力、艏搖力矩和橫傾力矩的幅值均隨運動幅值的增加而增大。

根據無因次水動力時歷曲線求得的水動力導數如表5所示。各旋轉導數誤差均在15%以內。

3.3漂角和艏搖組合運動計算結果

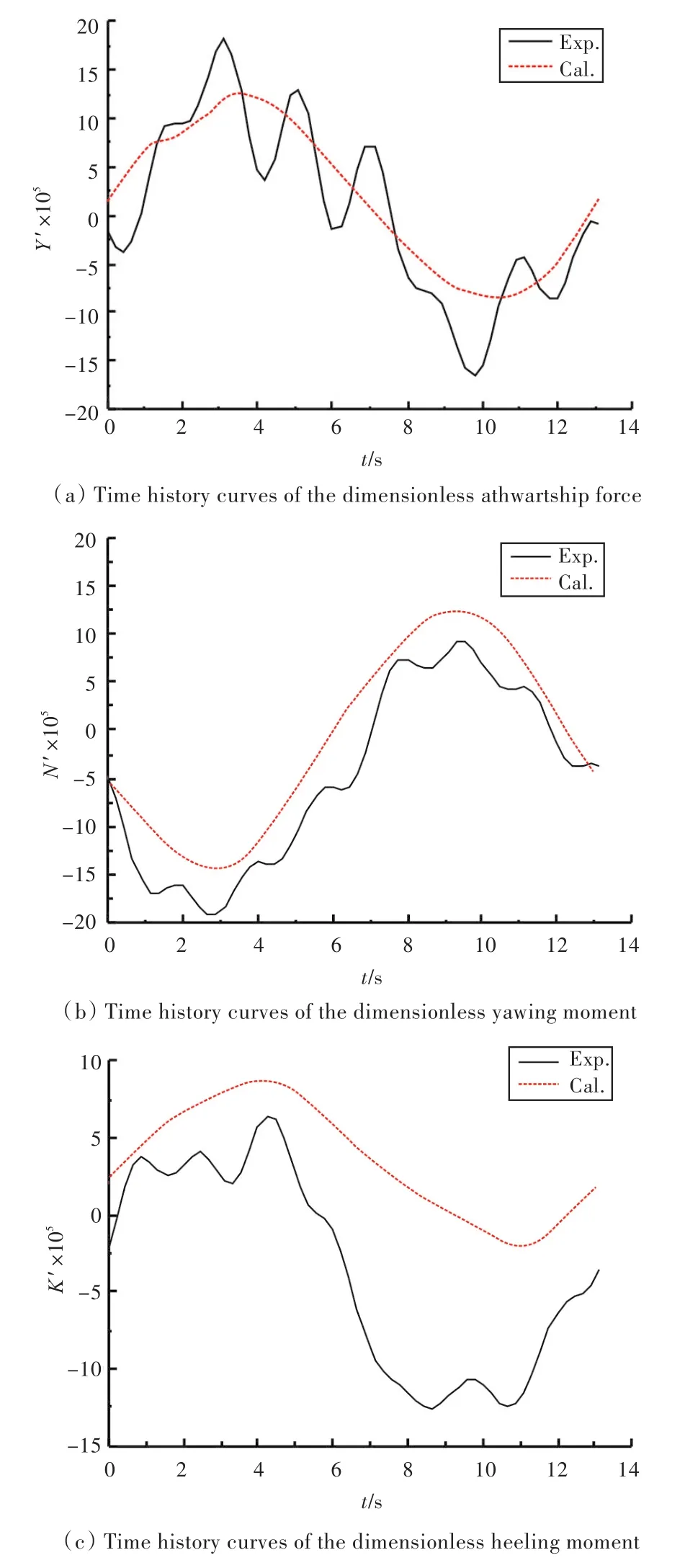
圖8　振幅為0.15 m時船模所受無因次水動力時歷曲線Fig.8　Time history curves of the dimensionless hydrodynamics when the amplitude is 0.15 m

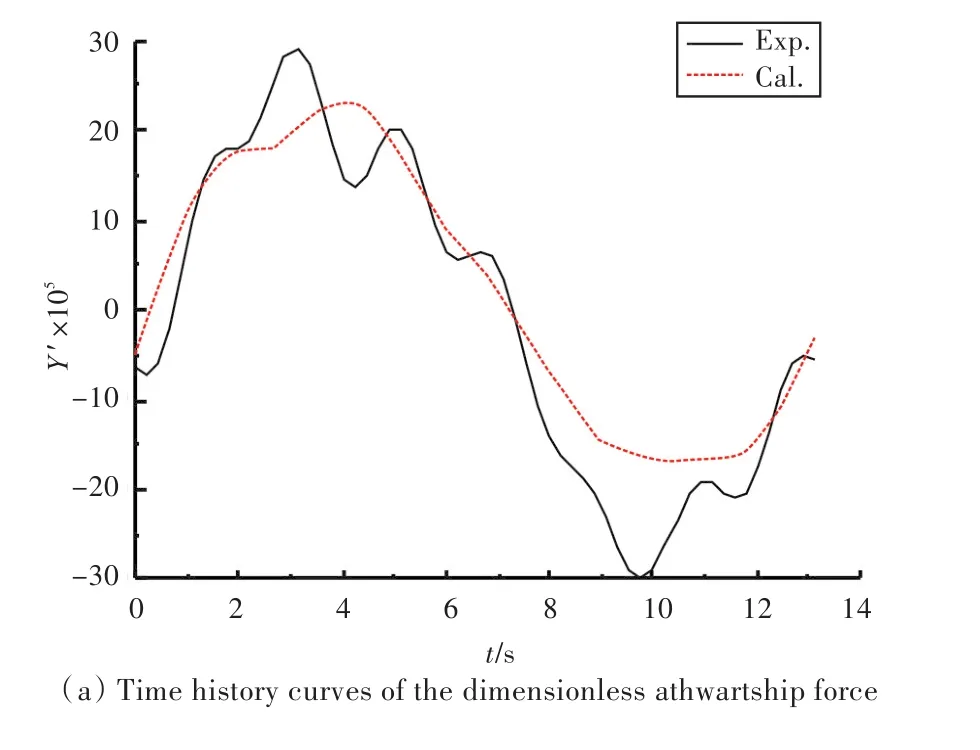
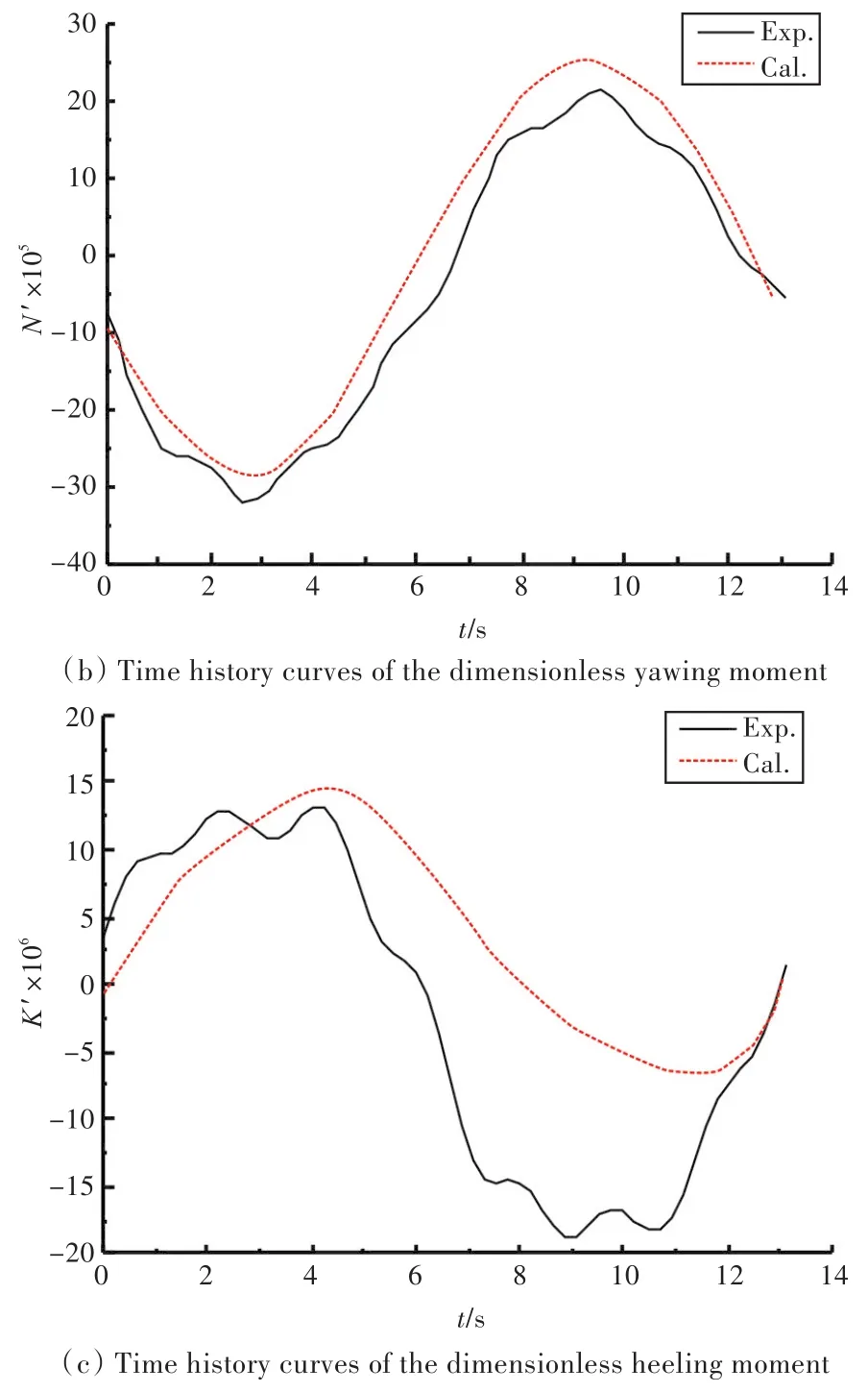
圖9　振幅為0.3 m時船模所受無因次水動力時歷曲線Fig.9　Time history curves of the dimensionless hydrodynamics when the amplitude is 0.3 m

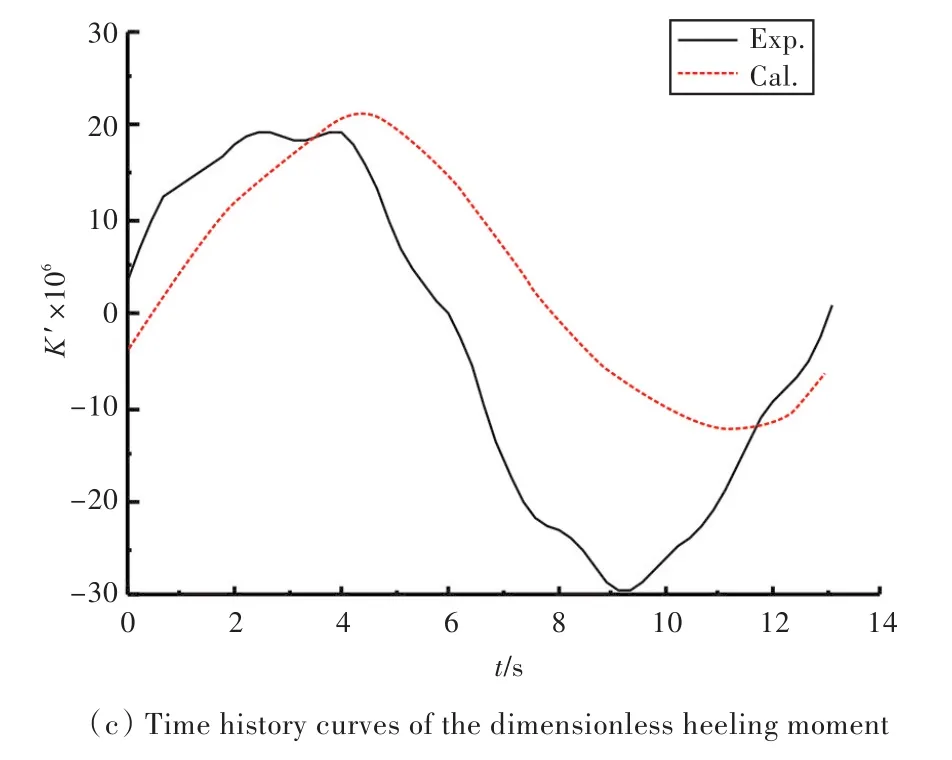
圖10　振幅為0.45 m時船模所受無因次水動力時歷曲線Fig.10　Time history curves of the dimensionless hydrodynamics when the amplitude is 0.45 m

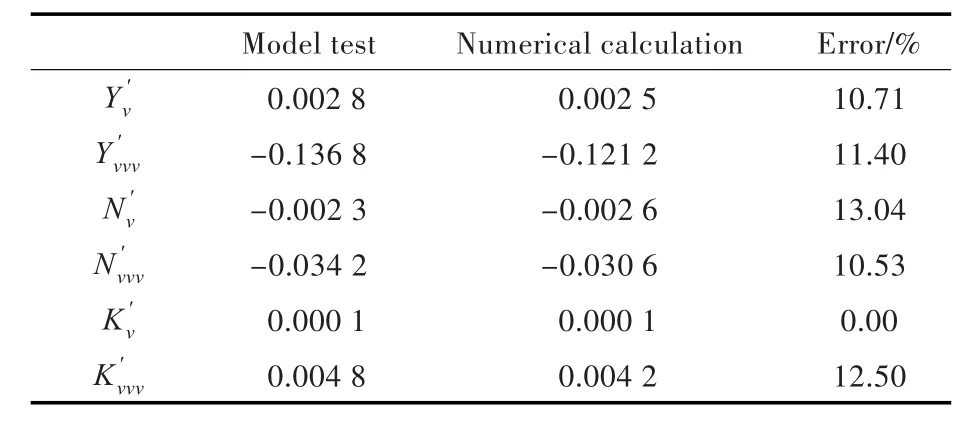
表5　純艏搖運動中水動力導數計算結果Tab.5　The calculation results of the hydrodynamic derivatives in the yaw motion

船模運動穩定后，選取一個周期內的數值模擬結果進行分析。船模所受的無因次水動力時歷曲線如圖11所示。由圖可知：對于橫向力，在前半個周期內，試驗和計算結果均先增大后減小，再增大；艏搖力矩的試驗與計算結果吻合較好，符合簡諧規律；橫傾力矩的計算與試驗結果相差略大，其原因與純艏搖運動中橫傾力矩的試驗與計算結果誤差略大相同。

根據無因次水動力曲線求得的水動力導數如表6所示。耦合導數誤差均在16%以內。

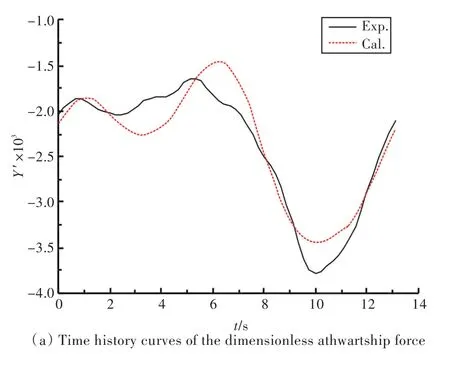
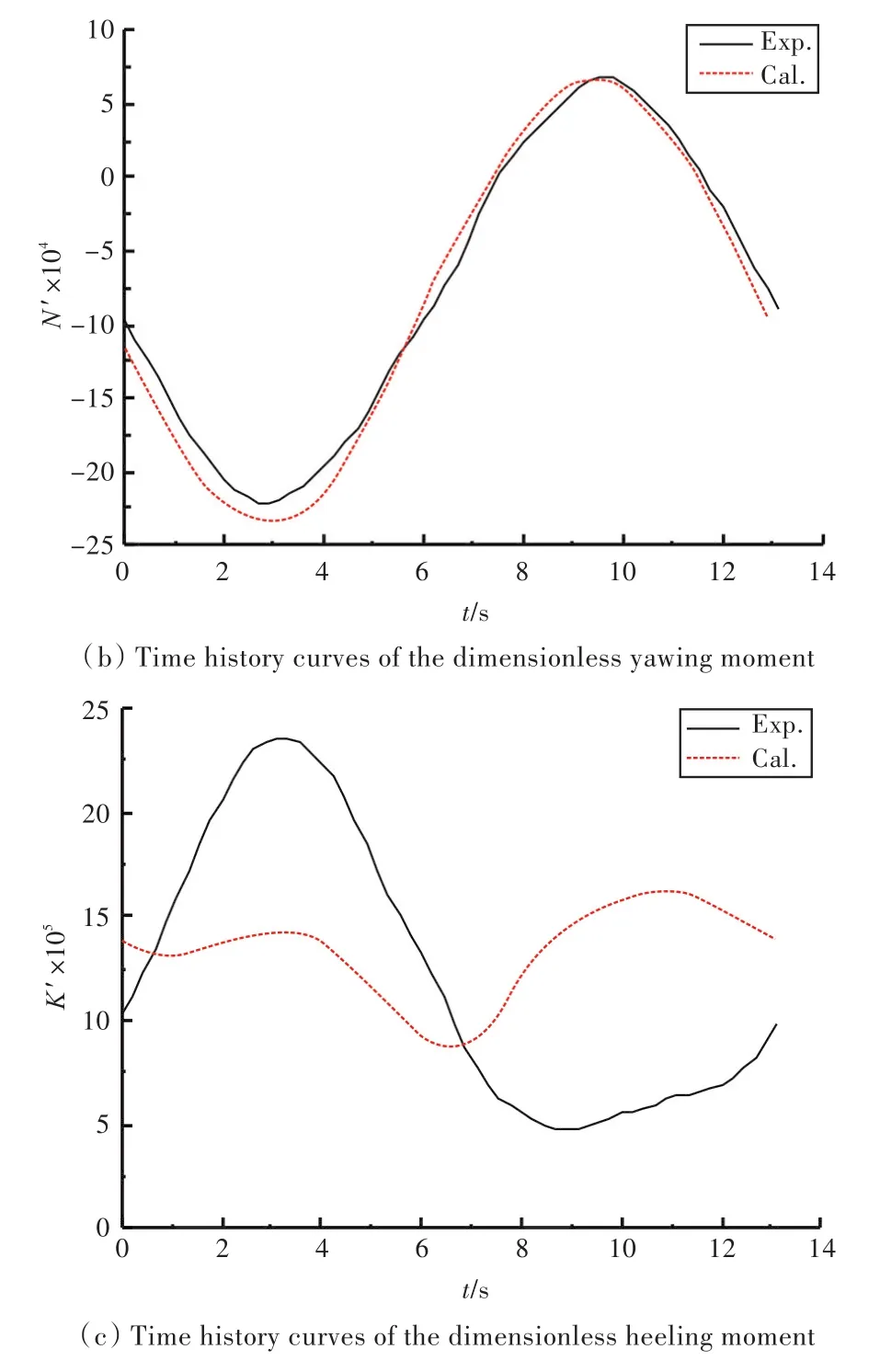
圖11　船模所受無因次水動力時歷曲線Fig.11　Time history curves of the dimensionless hydrodynamics

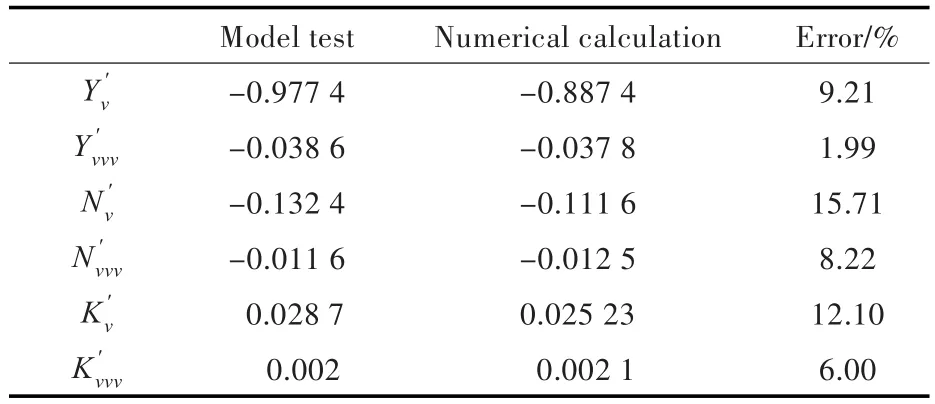
表6　漂角和艏搖組合運動中水動力導數計算結果Tab.6　The calculation results of the hydrodynamic derivatives in the combination of drift angle and yaw motion

4　結　語

本文基于star-ccm+軟件平臺，以全附體KCS船模為研究對象，應用體積力法模擬真實螺旋槳作用，開展了該船斜航、純艏搖、漂角和艏搖組合的PMM運動模擬研究，獲得了以下結論：

1）將體積力法應用到螺旋槳的處理上，大幅降低了網格數量，提高了計算效率。

2）研究的對象為全附體KCS型船模，且考慮了自由面興波及運動中船模姿態變化這些條件的影響，更真實地模擬了PMM試驗，采用理論分析方法求解的水動力導數誤差在20%以內，提高了計算精度。

［1］ BROGLIA R，DI MASCIO A，AMATI G.Aparallel unsteady RANS code for the numerical simulations of free surface flows［C］//Proceedings of the 2nd International Conference on Marine Research and Transportation.Naples，Italy：［s.n.］，2007.

［2］ BROGLIA R，MUSCARI R，DIMASCIO A.Numerical simulations of the pure sway and pure yaw motion of the KVLCC-1 and 2 tanker［C］//Proceedings of SIMMAN 2008 Workshop on Verification and Validation of Ship Maneuvering Simulation Methods.Lyngby，Demark：［s.n.］，2008.

［3］TYAGI A，SEN D.Calculation of transverse hydrodynamic coefficients using computational fluid dynamic approach［J］.Ocean Engineering，2006，33（5/6）：798-809.

［4］SAKAMOTO N，CARRICA PM，STERN F.URANS simulations of static and dynamic maneuvering for surface combatant［C］//Proceedings of SIMMAN 2008 Workshop on Verification and Validation of Ship Maneuvering Simulation Methods.Lyngby，Demark：［s. n.］，2008.

［5］ GUILMINEAU E，QUEUTEY P，VISONNEAU M，et al.RANS simulations of a US Navy frigate with PMM motions［C］//Proceedings of SIMMAN 2008 Workshop on Verification and Validation of Ship Maneuvering Simulation Methods.Lyngby，Demark：［s.n.］，2008.

［6］MILLER R W.PMM calculations for the bare and appended DTMB 5415 using the RANS solver CFDSHIP-IOWA［C］//ProceedingsofSIMMAN2008 Workshop on Verification and Validation of Ship Maneuvering Simulation Methods.Lyngby，Demark：［s.n.］，2008.

［7］劉山.基于CFD技術數值模擬平面運動機構試驗［D］.武漢：武漢理工大學，2012.

LIU Shan.Numerical simulation of planar motion mechanism test based on CFD technology［D］.Wuhan：Wuhan University of Technology，2012.

［8］程捷，張志國，蔣奉兼，等.平面運動機構試驗的數值模擬［J］.水動力學研究與進展，2013，28（4）：460-464. CHENG Jie，ZHANG Zhiguo，JIANG Fengjian，et al. Numerical simulation of the planar motion mechanism tests［J］.Chinese Journal of Hydrodynamics，2013，28 （4）：460-464.

［9］楊路春，龐永杰，黃利華，等.潛艇PMM實驗的CFD仿真技術研究［J］.艦船科學技術，2009，31 （12）：12-17.

YANG Luchun，PANG Yongjie，HUANG Lihua，et al.Study of the CFD approach to simulate PMM experiments of submarine［J］.Ship Science and Technology，2009，31（12）：12-17.

［10］ 樓鵬宇.限制水域中純橫蕩運動船體水動力數值計算［D］.上海：上海交通大學，2012.

LOU Pengyu.Numerical calculation of the hydrodynamic forces on a ship in pure sway motion in restricted waters［D］.Shanghai：Shanghai Jiao Tong University，2012.

［11］石愛國，聞虎，李理，等.船舶淺水水動力導數的數值計算［J］.中國航海，2011，34（3）：69-73，83.

SHI Aiguo，WEN Hu，LI Li，et al.Computation of hydrodynamic derivatives for ships in shallow water［J］.Navigation of China，2011，34（3）：69-73，83.

［12］吳召華，陳作鋼，代燚，等.基于體積力法的船舶回轉運動水動力數值研究［J］.中國艦船研究，2013，8（4）：12-19.

WU Zhaohua，CHEN Zuogang，DAI Yi，et al.Numerical study of hydrodynamic force on ships in turning motion based on a body-force propeller model［J］. Chinese Journal of Ship Research，2013，8（4）：12-19.

［13］吳召華，陳作鋼，代燚.基于體積力法的船體自航性能數值預報［J］.上海交通大學學報，2013，47 （6）：943-949.

WU Zhaohua，CHEN Zuogang，DAI Yi.Numerical prediction of self-propulsion with a body-force propeller model［J］.Journal of Shanghai JiaoTong University，2013，47（6）：943-949.

Numerical simulation on planar motion mechanism of KCS ship model with a body-force propeller model

WANG Huiting，BI Yi
Department of Naval Architecture Engineering，Naval University of Engineering，Wuhan 430033，China

In order to solve the ship maneuvering hydrodynamic derivatives efficiently and accurately，full-appendage KCS ship model is taken in this paper as the studying object.Based on RANS equation and VOF model，a descriptive body-force model is established to represent real propellers on the star-ccm+；the influences of the free surface wave and motion attitudes change on hydrodynamic are taken into account.The oblique motion，the yaw motion，the combination of yaw and drift angle motion on Planar Motion Mechanism（PMM）are simulated，and the athwartship force Y，the yawing moment N，and the heeling moment K are also acquired.The simulation results are then compared with the actual test results:according to the dynamics equation of PMM test，the time history curves of numerical and experimental results are analyzed with least-squares fitting and Fourier integral，where the hydrodynamic derivatives of manipulation are finally obtained.The results demonstrate the feasibility of the proposed method in PMM simulation，though the errors ofY′vvvandN′vvvare slightly larger，the errors of remaining hydrodynamic derivatives are all below 15%.

body-force propeller model；KCS ship model；Planar Motion Mechanism（PMM）；hydrodynamic derivatives

U661.3

A

10.3969/j.issn.1673-3185.2016.04.005

2015-10-23網絡出版時間：2016-7-29 9:45

水動力學重點基金資助項目（9140A14030712JB11044）；海軍工程大學自然科學基金資助項目（435517J4040）

王慧婷（通信作者），女，1990年生，碩士。研究方向：艦船流體動力性能。

E-mail：whut_wht@163.com

畢毅，男，1963年生，碩士，副教授。研究方向：艦船操縱性。E-mail：kpzc2002@163.com