預應力錨索內錨固段剪應力分布規律研究*

李金華，朱海西，宋　濤

(西安科技大學 建筑與土木工程學院，陜西 西安 710054)

?

預應力錨索內錨固段剪應力分布規律研究*

李金華，朱海西，宋濤

(西安科技大學 建筑與土木工程學院，陜西 西安 710054)

為研究預應力錨索內錨固段剪應力分布規律，基于B Benmokrane三階段線性函數建立錨固體與孔壁界面的剪切滑移本構模型，采用荷載傳遞函數法，對預應力錨索內錨固段剪應力沿軸向的分布規律進行理論研究，得到了不同狀態下剪應力沿錨固段軸向的分布特征方程，然后結合實際工程對預應力錨索不同工作狀態進行分析討論。結果表明：不同狀態下錨固段剪應力沿軸向分布不同，最大剪應力逐漸向錨固段內側轉移，在彈性變形階段之后剪應力達到峰值此后保持不變；預應力錨索進入殘余變形階段后，塑性區長度不再發生變化。研究結果可為預應力錨索的設計和工程應用提供理論依據。

預應力錨索；內錨固段；剪應力分布；極限承載力

0　引　言

在煤礦開采中，預應力錨索得到廣泛的應用，預應力錨索可以有效的減少頂板下沉量及巷道的收斂，提高圍巖穩定性[1-2]。在預應力錨索內錨固段受力機理的研究中，關于剪應力分布的具體形式，存在不同的結論。利用彈性力學對預應力錨索錨固段剪應力分布進行研究得到錨固段剪應力在起點處為零，之后逐漸增大至峰值點，隨后逐漸減小形成單峰曲線[3-7]。采用荷載傳遞法分析得到剪應力分布很不均勻，剪應力主要分布在錨固段端部4.5 m范圍內[8]。現場試驗研究表明，內錨固段剪應力分布是很不均勻的，剪應力達到峰值點后，隨錨固長度的增大基本上是呈負指數函數關系衰減[9]。數值模擬研究表明，剪應力最大值主要集中在錨固段前端，自錨固段端部逐漸增大至最大值后再趨變小，且呈指數函數關系分布[10]。現場監測和數值模擬表錨固段增大并不能有效提高錨索的承載能力，對錨桿長度進行優化后仍可以滿足穩定性要求[11-12]。但由于理論分析的假設與實際工程的不相符性，因此，有必要對錨固段剪應力的分布規律做進一步分析，以便尋求更加符合實際的結論。

文中基于錨固體與孔壁之間的剪切滑移模型，采用荷載傳遞函數法，建立彈塑性理論空間模型，對預應力錨桿錨固段剪應力沿長度方向的分布規律進行理論研究。

1　錨固段力學模型的建立

B.Benmokrane[13]等采用三階段線性函數來描述預應力錨桿錨固段巖體與錨固體之間的接觸面上的剪應力—剪切位移關系(圖1)，第Ⅰ階段對應于彈性階段，接觸面上剪應力與剪切位移成比例變化。第Ⅱ階段對應于接觸面的軟化損傷階段，采用降模量來描述接觸面上剪應力隨剪切位移增長而降低的性質。第Ⅲ階段對應于接觸面上的殘余強度，此時接觸面處于完全損傷狀態，只有摩擦阻力存在。

圖1　巖土體剪切位移關系Fig.1　Shear displacement relationship of rock and soil

圖2　預應力錨索作用機理Fig.2　Mechanism of prestressed anchor cable

三階段線性函數模型的剪應力—位移關系如圖1所示，用公式可以表示為

τ=Ku+ξ,

(1)

式中τ為剪應力；u為剪切位移；K,ξ均為材料參數，可以通過試驗確定。圖1中τ1為錨固段極限粘結強度；τ2為錨固段殘余粘結強度；u1為錨固段極限粘結強度對應的剪切位移；u2為錨固段殘余粘結強度對應的最小剪切位移。

在錨索錨固段任意處z取錨固體微段dz(圖3)，利用胡克定律，由應變和力的平衡關系可得

圖3　錨索微段靜力平衡Fig.3　Static equilibrium of anchor micro section

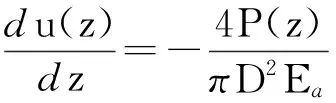
(1)

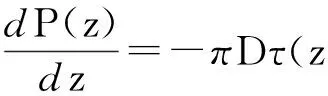
(2)

則聯合方程(1)、(2)有

(3)

1.1錨固體與圍巖界面荷載傳遞彈性分析

當界面處于第Ⅰ階段(彈性狀態)時，線性傳遞函數為[9]

τ(u)=K1u,

(4)

u(z)=C1cosh(βz)+C2+sinh(βz),

(5)

考慮邊界條件：在錨固段始端P|z=0=P，錨固段尾端P|z=Lb=0，結合(2)可得

(6)

相應的，錨固體與圍巖界面剪應力分布公式為

(7)

當錨固層處于彈塑性臨界情況下時，z=0處側阻力剛好達到界面極限粘結強度，于是令τ(z)=τ1可得錨固層處于彈性狀態的極限抗拔力為

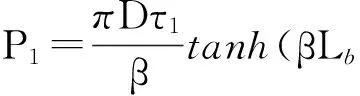
(8)

1.2錨固體與圍巖界面荷載傳遞彈塑性分析

當界面處于第Ⅱ階段(彈塑性狀態)時，線性傳遞函數為

τ(u)=τ1-K2(u-u1),

(9)

將(9)代入平衡微分方程(3)得到

(10)

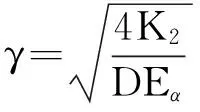
u(z)=τ1/K2+u1+C3cos(γz)+C4sin(γz),

(11)

τ(z)=-K2[C3cos(γz)+C4sin(γz)],

(12)

(13)

當錨固層處于彈塑性臨界情況下時，有邊界條件②：τ|z=0=τ2，τ|z=Ze=τ1代入(12)可得

(14)

(15)

分別將l帶入C3，C4，并帶入式(12)、(13)則可求出錨固體與圍巖界面剪應力分布函數為

(16)

軸力分布函數為

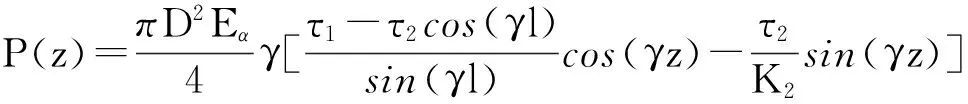
(17)

則有可求彈塑性狀態的極限抗拔力為

(18)

1.3錨固體與圍巖界面進入殘余變形階段分析

當界面處于第Ⅲ階段(殘余變形)時，線性傳遞函數為

τ(u)=τ2,

(19)

錨固體與圍巖界面剪應力分布函數為

τ(z)=τ2,

(20)

錨索的軸力為

P(z)=P-πDτ2z.

(21)

2　結果與討論

以西安某基坑工程為例對理論推導進行討論。試驗段土體為黃土體，較完整，預應力錨索總長度為20m，錨固長度為9m，錨索孔孔徑為150mm，錨索鋼采用4As15.2mm的鋼絞線，注漿體為純水泥漿液。鋼絞線的彈性模量為1.95×105MPa，注漿體的彈性模量為2.5×104MPa.現場試驗可得材料常數K1=600MPa·m-1，K2=300MPa·m-1，注漿體極限粘結強度τ1=900kPa，注漿體殘余粘結強度τ2=360kPa.

2.1錨固體處于彈性階段分析

帶入相關參數，由式(8)可得錨索的彈性極限承載力為P1=573kN，圖4分別給出錨索拉拔力為200，300，400，500和573kN時錨索錨固段剪應力沿錨固長度分布圖。

圖4　彈性階段各荷載下錨固段剪應力分布曲線Fig.4　Shear stress distribution curves of different load in elastic stage

從圖4可以看出，錨索在彈性階段工作時，各荷載下剪應力峰值出現在錨固段端口，沿錨固段長度方向逐漸減小至0；隨著荷載的增大，剪應力峰值也在增大，荷載達到彈性極限承載力時，端口剪應力達到τ1最大；剪應力主要集中在錨固段前6 m左右。

2.2錨固體處于彈塑性階段分析

帶入相關參數，由式(18)可得錨索的彈塑性極限承載力為P2=743 kN，在彈塑性極限承載力作用下錨固段塑性區的長度l=2.21 m.圖5分別給出錨索拉拔力為573，600和743 kN時，錨索錨固段剪應力沿錨固長度分布曲線。

圖5　彈塑性階段各荷載下錨固段剪應力分布曲線Fig.5　Shear stress distribution curves of different load in elastic-plastic stage

從圖5可以看出，錨索進入彈塑性階段工作時，剪應力分布很不均勻，錨固段端口剪應力隨拉拔荷載的增大從τ1減小至τ2；剪應力主要集中在錨固段前7 m左右；隨著荷載的增大剪應力峰值大小為τ1不變，位置逐漸向里擴展，錨固段塑性區變長，最終達到彈塑性極限狀態。

2.3錨固體進入殘余變形性階段分析

錨固體進入殘余變形性階段時，分別取拉拔力為743,850和1 000 kN進行計算分析(圖6)。

圖6　殘余變形階段各荷載下錨固段剪應力分布曲線Fig.6　Shear stress distribution curves of different load in residual deformation stage

當錨固體進入殘余變形階段時，其殘余變形階段剪應力不變，之后的剪應與錨索彈塑性剪應力分布趨勢基本一致；各荷載下錨固段塑性區長度為2.21 m不變；當錨固段局部出現殘余變形時，錨固體和周圍土體產生相對位移，出現裂縫，隨著荷載的增大，裂縫會迅速向里擴展，錨索最終破壞，因此，此階段的承載力并不能作為錨索的最終極限承載力。

3　結　論

1)采用剪切滑移模型推導的錨固體與巖土體界面剪應力分布公式，給出了錨索極限承載力的計算公式，便于工程應用；

2)隨著拉拔荷載的增加，錨索錨固段剪應力的峰值逐漸向遠端偏移，其分布深度也不斷地向下擴展，但其剪應力峰值的大小不變；

3)預應力錨索錨固段剪應力分布很不均勻，在黃土地層中剪應力主要分布在錨固段前7 m范圍內，錨索的極限抗拔力P2與錨索錨固長度無關；

4)預應力錨索錨固段處于彈塑性變形階段后，其塑性區的長度為定值，不會隨著拉拔力荷載而改變。

References

[1]柳選軍，劉慶利，朱世陽，等.深井長距離大斷面回采巷道支護方案優化[J].西安科技大學學報，2015，35(1)：28-31.

LIU Xuan-jun，LIU Qing-li，ZHU Shi-yang，et al.Supporting scheme optimization for long distance and large dimension entry of deep mine[J].Journal of Xi’an University of Science and Technology，2015，35(1)：28-31.

[2]贠東風，李尚明，蘇普正，等.瑞能煤礦區段煤柱中巷支護技術[J].西安科技大學學報，2012，32(4)：434-438，458.

YUN Dong-feng，LI Shang-ming，SU Pu-zheng，et al.Technology of roadway supporting in middle of sectional coal pillar in Ruineng colliery[J].Journal of Xi’an University of Science and Technology，2012，32(4)：434-438，458.

[3]張端良，董燕軍，唐樂人.預應力錨索錨固段周邊剪應力分布特性的彈性理論分析[J].巖石力學與工程學報，2004，23(S2)：4 735-4 738.

ZHANG Duan-liang，DONG Yan-jun，TANG Le-ren.Elasticity analysis on distribution of shear stress along anchoring section of prestressed anchor cable[J].Chinese Journal of Rock Mechanics and Engineering,2004，23(S2)：4 735-4 738.

[4]李桂臣，孫輝，張農，等.基于錨索剪應力分布規律的新型高強錨索束應用研究[J].煤炭學報，2015，40(5)：1 008-1 014.

LI Gui-chen，SUN Hui，ZHANG Nong，et al.Application research on new high-strength anchor cable bundle based on the shear stress distribution of anchor cable[J].Journal of China Coal Society，2015，40(5)：1 008-1 014.

[5]尤春安，戰玉寶.預應力錨索錨固段的應力分布規律及分析[J].巖石力學與工程學報，2005，24(6)：925-928.

YOU Chun-an，ZHAN Yu-bao.Distributing characters and analysis of stresses in prestressed cables[J].Chinese Journal of Rock Mechanics and Engineering,2005，24(6)：925-928.

[6]蔣忠信.拉力型錨索錨固段剪應力分布的高斯曲線模式[J].巖土工程學報，2001，23(6)：696-699.

JIANG Zhong-xin.A gauss curve model on shear stress along anchoring section of anchoring rope of extensional force type[J].Chinese Journal of Geotechnical Engineering，2001，23(6)：696-699.

[7]李金華，袁兵.土層中錨索拉拔力與位移關系的研究[J].煤炭科學技術，2010，38(3)：32-34，38.

LI Jin-hua，YUAN Bing.Research on relationship between anchor pulling capacity and displacement in soil[J].Coal Science and Technology，2010，38(3)：32-34，38.

[8]谷拴成，陳弦，葉根飛.考慮孔壁界面剪切滑移錨桿錨固段應力分布[J].礦業研究與開發，2010，30(2)：34-36，93.

GU Shuan-cheng，CHEN Xian，YE Gen-fei.Stress distribution of anchorage section of prestressed rock bolt considering the shearing slip effect of grout-rock interface[J].Mining Research and Development，2010，30(2)：34-36，93.

[9]沈俊，顧金才，張向陽，等.拉力型和壓力型自由式錨索現場拉拔試驗研究[J].巖石力學與工程學報，2012(S1)：3 291-3 297.

SHEN Jun，GU Jin-cai，ZHANG Xiang-yang，et al.Field pull-out test research on tension and pressure unbonded anchor cables[J].Chinese Journal of Rock Mechanics and Engineering,2012(S1)：3 291-3 297.

[10]徐前衛，尤春安，朱合華.預應力錨索的三維數值模擬及其應用研究[J].巖石力學與工程學報，2004(S2)：4 941-4 945.

XU Qian-wei，YOU Chun-an，ZHU He-hua.Study on 3D numerical simulation of prestressed anchor cable and its application[J].Chinese Journal of Rock Mechanics and Engineering,2004(S2)：4 941-4 945.

[11]張雪媛.深井巖巷破壞機理與支護優化研究[J].西安科技大學學報，2014，34(4)：390-395.

ZHANG Xue-yuan.Failure mechanism and support of deep rock roadway[J].Journal of Xi’an University of Science and Technology，2014，34(4)：390-395.

[12]孟慶彬，韓立軍，喬衛國，等.唐口煤礦深部軟巖巷道支護技術研究[J].西安科技大學學報，2012，32(2)：164-171.

MENG Qing-bin，HAN Li-jun，QIAO Wei-guo，et al.Support technology for deep soft rock roadway of Tangkou coal mine[J].Journal of Xi’an University of Science and Technology，2012，32(2)：164-171.

[13]Benmokrane B，Chennouf A，Mitri H S.Laboratory evaluation of cement-based grouts and grouted rock anchors[J].International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts，1995，32(7)：633-642.

Shearing stress distribution along anchoring section of pre-stressed anchor cable

LI Jin-hua，ZHU Hai-xi，SONG Tao

(CollegeofCivilandArchitecturalEngineering，Xi’anUniversityofScienceandTechnology，Xi’an710054，China)

In order to research the shearing stress distribution of anchored section，based on the shearing displacement structure of B.Benmokrane’s three stage linear functions of relationship between the anchoring body and borehole wall face，we adopt the load transmission method to research the distribution law of shear stress along the length direction of anchor blot direction.Then combined with the actual project，the different working states of pre-stressed anchor cable are analyzed and discussed.The results show that：The shear stress along the axial are different in different states.The maximum shear stress gradually shifts to the inner anchoring section and the peak stress will not change after the elastic deformation stage；The length of the plastic zone will not change after the pre-stressed anchor enters the stage of residual deformation.The study is of a reference for pre-stressed anchor design and application.

pre-stressed anchor cable；anchored section；shearing stress distribution；ultimate bearing capacity

10.13800/j.cnki.xakjdxxb.2016.0313

1672-9315(2016)03-0375-05

2016-01-12責任編輯：李克永

國家自然科學基金(51508462);陜西省教育廳基金(2013JK0961)

李金華(1977-),男,山東滕州人,副教授,E-mail:nxljh@xust.edu.cn

TD 353

A