求解動態車間調度問題的改進微粒群算法

吳再新，高尚策，2，齊 潔

（1.東華大學 信息科學與技術學院，上海　201620；2.富山大學 工程學院，日本 富山　9308555）

求解動態車間調度問題的改進微粒群算法

吳再新1，高尚策1，2，齊 潔1

（1.東華大學 信息科學與技術學院，上海201620；2.富山大學 工程學院，日本 富山9308555）

為了對生產車間調度過程中發生的動態事件進行快速、有效的處理，提出了一種將微粒群算法與遺傳算法（GA）、模擬退火算法（SA）相結合的混合微粒群算法（GSPSO）。通過用標準車間調度問題對該算法的性能進行檢驗；然后把該算法用于解決基于事件驅動調度策略的動態車間調度問題；仿真結果表明GSPSO算法具有快速的收斂性和可行性，能對生產過程中發生的動態事件進行合理調度。

動態車間調度；粒子群算法；遺傳算法；事件驅動

對生產作業車間進行有效的調度是制造執行系統的一項核心技術，也是研究的一個熱點問題。作業車間調度問題（JSP）實際上就是組合優化問題，也是一類典型的NP難題，它可以分為兩種：靜態調度和動態調度。在過去的幾十年里，大部分學者對于車間調度問題的研究都是靜態的。在實際的生產過程當中，各種突發事件（如新增緊急訂單、訂單取消、機器故障等）時常發生，因此動態作業車間調度更加符合實際的情況。

在求解JSP問題的方法上，遺傳算法憑借其強大的全局搜索能力，被許多學者用于解決JSP問題[1]，但是該算法有收斂速度慢、容易早熟的缺點；蟻群算法主要針對調度問題產生，其在解決JSP問題上也得到了大量的應用[2]，該算法對大規模調度問題很難得到最優解，且求解時間過長。粒子群優化算法是Dr.Eberhart與J.Kennedy于1995年正式提出[3]，之后得到了迅速的發展和廣泛的應用，文獻[4]采用微粒群算法與遺傳算法相結合，提出了改進的微粒群算法用于解決模糊車間調度問題，但是對算法跳出局部最優的策略仍待改進。在前人研究的基礎上，把遺傳算法交叉變異特性和模擬退火算法的metropolis接受準則引入到PSO算法中，提出了混合微粒群算法（GSPSO）用于解決作業車間調度問題。

1　動態車間調度（DJSP）

JSP問題可以簡單的描述為:有n個工件在m臺機器上進行加工，每個工件有一道或者多道工序等待加工，每道工序只能在指定的機器上進行加工，且滿足以下的約束條件[5]：

1）每個工件的加工工序不能改變。

2）每個工件的加工時間和機器事先已經確定。

3）同一工件同一時刻只能在一臺機器上進行加工。

4）一臺機器同一時刻只能加工一個工件。

調度的目的就是找到一個合適的加工序列，在滿足上述約束條件的情況下，使得最大加工完成時間最小。所謂最大加工完成時間就是所有工件中最后一道工序加工完成的時間，可用式（1）表示：

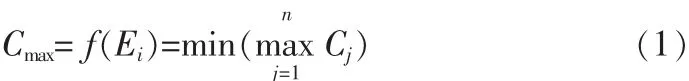
其中，表示最佳的調度方案，表示工件最后一道工序的完工時間。

在實際的生產過程中，一些隨機的動態事件比如新增緊急訂單，訂單取消，機器故障維修等在所難免，在任務執行過程中必須實時監測這些隨機事件的發生，然后對加工任務執行重新調度，使得調度系統始終處于最優狀態。這樣，原本是靜態的作業車間調度就變成了動態調度。解決動態事件的策略有兩種[6]，一是基于事件驅動的調度策略，即在系統動態事件發生時就立即進行重調度。二是周期性的調度策略，即不管有無動態事件發生，系統總是每隔一段時間進行一次重調度。在實際的生產應用當中，應視情況而選取不同的調度策略，當已知系統會周期性的出現動態事件（如定期機器維修）時，應采用周期性調度策略；當系統對動態事件處理的實時性要求比較高時應選取事件驅動的調度策略。為了使最大完工時間最小，又要使系統對動態事件做出及時的響應，減少重調度帶來的時間損耗，本文選用基于事件驅動的調度策略。

2　GSPSO算法描述

2.1標準微粒群優化算法

微粒群優化算法是基于群體尋優的進化算法，它將每個個體看作是D維搜索空間中的一個沒有體積的微粒，每個微粒都代表極值優化問題的一個潛在最優解，用位置、速度和適應度值三項指標表示該微粒的特性適應度值由適應度函數計算而來，其值的好壞表示粒子的優劣。微粒在解空間中運動，通過跟蹤個體極值Pbest和群體極值Gbest更新個體位置。個體極值Pbest是指個體所經歷位置中計算得到的適應度值最優位置，群體極值Gbest是指種群中所有粒子搜索到的適應度最優位置。其優化過程可用下式表示[7]：

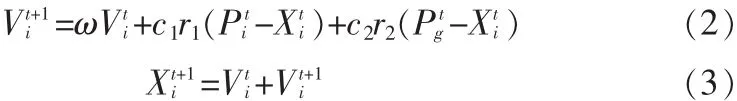
其中，為慣性權重，為粒子速度，、為非負常數，稱為加速度因子，和是分布在[0，1]區間的隨機數。標準微粒群尋優算法的基本流程圖如圖1所示。

圖1　標準微粒群算法流程Fig.1　The standard PSO algorithm flow chart

2.2GSPSO算法概述

微粒群優化算法是針對連續優化問題提出，而要用于解決離散問題必須對算法進行改進。由式（2）和式（3）可知，微粒具有自身的認知能力和社會信息共享能力，這也是種群進化的依據。為了能使用PSO算法對離散的JSP問題進行處理，文中提出了式（4）用于粒子更新：

式中表示粒子的第t+1次迭代，、分別表示粒子的個體極值和種群的群體極值，茚代表遺傳算法的交叉操作，、分別代表粒子與、交叉時交叉片段的長度，他們的取值范圍是0到微粒的最大長度。由此可知，為粒子的自身的認知能力，為種群的社會信息共享能力，而則表示當前粒子的權重。

標準的PSO算法具有快速的收斂能力，但是容易陷入局部最優解。將SA算法的metropolis接受準則融入到PSO算法中，使算法具有突跳能力，能有效的避免搜索過程陷入局部最優解。把GA算法的變異操作作用于PSO算法的全局最優解，增加種群的多樣性，能使算法得到全局最優解。GSPSO算法同時繼承了3個算法的優點，使得它能夠快速的在全局范圍內尋找最優解，又能避免算法在搜索過程中陷入局部最優解。GSPSO算法的解決動態車間調度問題的基本步驟如下：

Step1：種群初始化，初始種群尋優

采用基于工序的編碼方式隨機生成初始微粒種群，通過適應度值函數對微粒進行評價，找出所有微粒的最佳個體，記為種群的最優個體，所有粒子的個體最優記為各自的初始位置。

Step2：SA算法Metropolis接受準則

將SA算法的Metropolis接受準則作用于個體最優微粒，避免算法陷入局部最優解。

Step3：遺傳算法的交叉與變異

把遺傳算法的交叉操作引入到PSO算法中粒子的進化過程當中，用交叉產生的新個體代替粒子的速度和位置的更新。同時把遺傳算法的變異策略作用到全局最優微粒，以避免算法陷入局部最優，增加種群的多樣性。

Step4：最優選擇

當算法達到算法的終止條件后，采用第二步選出來的全局最優粒子作為種群的最優值Gbest，選出最優值之后調度任務就可以順利進行了。當動態事件出現，調度任務被打斷時，進入第五步。

Step5：動態事件處理

通過動態事件發生的時刻可以確定待加工的工件和機器的狀態，重新進入第一步進行重調度。

2.3GSPSO算法的具體實現

GSPSO算法處理作業車間動態調度問題的算法流程圖如圖2所示。

2.3.1適應度值函數

PSO算法是通過適應度值函數來對個體的自身性能及種群的整體性能進行評價的，根據適應度的大小對個體進行優勝劣汰的選擇，進而決定個體的下一步操作。由于本文以調度任務的最大完工時間最少為優化目標，因此可以用式（1）的倒數作為算法的適應度值評價函數，即：

圖2　GSPSO算法流程圖Fig.2　The GSPSO algorithm flow chart

2.3.2Metropolis抽樣準則

在PSO算法中引入Metropolis準則，它能以一定的概率接受惡化解，這樣就能使算法跳離局部最優的陷進。接受概率是這樣確定的，假如調度任務最小的最大完工時間為f（t），則當前解最小的最大完工時間為，新解最小的最大完工時間為，兩者的差值為，則Metropolis準則接受概率為：

如果df<0，則以概率1接受新解；否則以概率exp（）接受新解。

2.3.3粒子的編碼規則

由于調度問題具有嚴格的工藝約束，必須以一定的編碼方式來體現其工藝約束，以便用微粒群算法對其進行處理。文中采用基于工序的編碼方式對調度任務進行編碼，該編碼方式進行編碼時，用同一數字表示工件的工件號，用該數字在微粒中第幾次出現來表示該工件的工序號。例如以一個3*3的作業車間調度問題為例，有一個粒子的編碼為232133211，該編碼的第一個數2表示2號工件的第一道工序，第二個數3表示3號工件的第一道工序，第三個數2表示2號工件的第二道工序，以此類推。

2.3.4遺傳算法的變異與交叉操作

為了使算法能夠在全局范圍內搜索最優解，避免進入局部最優解，增加種群的多樣性，對PSO算法中的以一定的概率進行變異操作。傳統遺傳算法的變異概率是固定不變的，從而使得算法難以跳出局部最優，文中提出一種新的計算變異概率的式（7），

式中為第i次迭代的變異概率，為初始變異概率，為第i次迭代中的適應度值函數，、分別為的最大適應度值函數和平均適應度值函數。這種方法能提高適應度值劣于平均適應度值微粒的變異概率，抑制適應度值優于平均適應度值微粒的變異概率。變異的方法是隨機的交換微粒中若干對工序的位置。

在PSO算法中，采用遺傳算法的交叉操作替代PSO算法的種群更新，可以有效的把其應用于解決離散的JSP問題。在交叉的過程中，先讓微粒與Pbest交叉，交叉的方法是根據式（4），在Pbest中選取一段，插入到當前微粒的對應位置，然后再把此微粒與Gbest進行交叉，交叉的方法與前面相同。這樣在交叉后就得到了新的微粒，新的微粒既保存的上一代微粒的信息，又具有信息共享的能力。以一個3*3的車間調度問題為例，假設式（4）中常數、都為2，則一個微粒的交叉過程可用如圖3來描述，交叉后會出現某些工件的工序多余，某些工件的工序缺失的現象，把工件工序多余的操作變為工件工序缺失的操作，使得交叉后的微粒符合編碼規則。

圖3　微粒交叉Fig.3　The cross of particle

2.4動態作業車間調度的實現過程

在調度系統的執行過程當中，由于調度環境的動態變化，需要對加工任務進行重新調度。重調度與初始時刻調度的主要差別是機器狀態和加工的工件任務不同，機器的可利用時候和工件上一道工序的完成時刻不同。在重調度時刻，有的機器可能正在加工工件，由于加工過程的連續性，只有待機器加工完該工序，才能進入重調度的調度安排；而有的機器可能在重調度時刻處于空閑狀態，重調度之后立即可以投入生產；有的工件可能完成了一部分工序，也有可能完成了全部工序。處理動態事件的步驟如下：

Step1：系統按照調度方案進行加工，動態事件發生時進入第二步，如果加工任務完成沒有動態事件發生，結束調度任務。

Step2：確定重調度加工工件的工序矩陣和對應的機器矩陣，通過動態事件發生的時候和初始調度情況計算機器的可利用時刻矩陣。

Step3：產生重調度方案，轉入第一步，調度任務繼續執行。

3　實驗仿真與分析

實驗仿真在自用PC機上進行，用benchmark車間調度問題對算法進行測試，算法的基本參數設置如下：

種群迭代次數，種群規模，粒子交叉片段常數、問題的規模大小不一適當變化，變異初始概率，模擬退火初始溫度，降溫系數。

表 1是用本文提出的算法和 PSOGA、GA算法解決benchmark車間調度問題10次，然后取平均值的比較。從表中可以看出，本文提出的PAGSO算法與另外兩種算法相比具有更好的平均值，從而表明該算法在求解JSP問題上具有很好的求解效果。

圖4是3種算法在求解FT06問題時的收斂性比較，圖中橫坐標表示算法的迭代次數，縱坐標表示最大完工時間10次的平均值。從圖中可知，PSGSO算法具有更快的收斂速度。

表1　三種算法的比較Tab.1　Comparison of the three algorithms

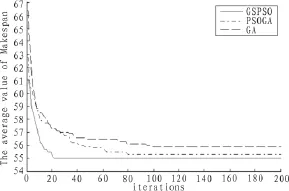
圖4　三個算法的收斂性比較Fig.4　The convergence comparison of the three algorithms

圖5是用本文提出的PSGSO算法解決DJSP問題時的輸出甘特圖，圖中橫坐標表示加工時間，縱坐標表示機器號。限于篇幅只考慮以下3種動態事件發生的情況：

圖5　動態調度甘特圖Fig.5　The gantt chart of the dynamic job-scheduling

1）新增緊急訂單。在t=20時刻，新增緊急訂單7號工件，該工件工序的時間約束矩陣為T7=[6 3 8 5 4 9]，對應的機器約束矩陣為M7=[6 1 5 2 4 3]，由圖可以看出緊急訂單加入后被優先處理，最終的調度結果為64。

2）在t=30時刻，取消4號和5號工件，由圖可知在30時刻后工件4和工件5的已經從調度任務中取消，最終的調度結果為52。

3）在t=26時刻，機器4出現故障，預計修復時間為9，最終調度結果為57。

文獻[8]中用混合蟻群算法解決同樣的問題，與本文采用的方法比較如表2所示，結果表明GSPSO算法具有明顯的優勢，說明該算法具有可行性。

表2　混合蟻群算法與GSPSO算法處理DJSP問題時的比較Tab.2　The comparison of ant colony algorithm and GSPSO algorithm to deal with DJSP

4　結束語

文中把遺傳算法的交叉、變異操作和模擬退火算法的Metropolis接受準則融入到粒子群[9-11]優化算法當中，形成了混合粒子群算法GSPSO，該算法能自適應的調整變異概率，在全局范圍內高效地搜索最優解。通過實驗結果表明該算法對小規模的JSP問題具有很好的搜索質量和較快的收斂速度，能對車間調度生產過程中發生的動態事件進行及時有效的處理；但是對大規模的JSP問題是否能取得好的效果還有待驗證，這也是今后研究的重點內容。

[1]ZHAO Zi-xiang，ZHANG Guo-shan，BING Zhi-gang.Jobshopscheduling optimization design based on an improved GA[C]//2012 10th World Congress on Intelligent Control and Automation（WCICA）.Beijing:IEEE，2012:654，659.

[2]雷蕾.基于混合蟻群算法的動態JSP研究與仿真[D].西安：西安工業大學，2012.

[3]Eberhart R，Kennedy J.A new optimizer using particle swarm theory[C]//Proceeding of the Sixth International Symposium on Micro Machine andHuman Science.Nagoya:IEEE，1995: 39-43.

[4]Niu Q，Jiao B，Gu X S.Particle swarm optimization combined with genetic operators for job-shop scheduling problem with fuzzy processingtime[J].Applied Mathematics and Computation，2008，205（1）:148-158.

[5]CHIANG Tsung-Che，FU Li-Chen.Multiobjective Job Shop Scheduling using Genetic Algorithm with Cyclic Fitness Assignment[C]//IEEE Congress on Evolutionary Computation. Vancouver BC:IEEE，2006:326-3273.

[6]SureshV，ChandhuriD.Dynamic Scheduling-A survey of research[J].Int Jof Prod Peon，1993，32（1）:53-63.

[7]YAN Ping，JIAO Ming-hai.Animproved PSO search method for the job shop scheduling problem[C]//Control and Decision Conference.Mianyang:IEEE，2011:23-25.

[8]陸韡，張潔.基于事件及變周期驅動的作業車間動態調度[J].控制工程，2007（S1）:209-213.

[9]孫會明，陳薇.基于粒子群優化的光伏MPPT算法[J].電子科技，2014（8）:187-189.

[10]康鯤鵬.快速混合粒子群優化算法應用研究[J].電子設計工程，2014（10）:10-13.

[11]王娟娟.哈夫曼編碼的協同粒子群優化算法[J].計算機與現代化，2015（6）:82-85.

An improved particle swarm optimization algorithm for dynamic job-shop scheduling problem

WU Zai-xin1，GAO Shang-ce1，2，QI Jie1
（1.College of Information Science and Technology，Dong Hua University，Shanghai 201620，China；2.Faculty of Engineering，University of Toyama，Toyama 9308555，Japan）

In order to deal with the dynamic events rapidly and effectively in the process of job-shop scheduling，an improved hybrid Particle Swarm Optimization algorithm（GSPSO）combining with Genetic Algorithm（GA）and Simulated Annealing algorithm（SA）has been proposed.The introduced algorithm is tested by the benchmark job-shop problem（JSP），then，the hybrid algorithm is used to solve the dynamic JSP problem which based on the event driven scheduling strategy.The results of the simulation shows the good convergence and feasible of the improved algorithm，and it can make a good performance in dealing with the uncertain dynamic events.

dynamic job-shop scheduling；particle swarm optimization algorithm；genetic algorithm；event driven

TP18

A

1674－6236（2016）01-0026-05

2015-05-09稿件編號：201505080

國家自然科學基金項目（61203325）；上海啟明星計劃項目（14QA1400100）

吳再新（1990—），男，湖南婁底人，碩士。研究方向:人工智能與智能控制。