月池對鉆井船阻力性能影響研究

張曉宇胡開業紀 元周雯雯（.中國石油渤海裝備研究院 海工裝備分院 盤錦400； .哈爾濱工程大學 船舶工程學院 哈爾濱5000）

月池對鉆井船阻力性能影響研究

張曉宇1胡開業2紀 元2周雯雯2
（1.中國石油渤海裝備研究院 海工裝備分院 盤錦124010； 2.哈爾濱工程大學 船舶工程學院 哈爾濱150001）

針對鉆井船海上航行工程背景，考慮浮態變化對鉆井船阻力的影響，采用粘性流體力學算法，對某艘有詳細實驗數據的鉆井船在靜水中的阻力性能進行計算與分析。通過研究網格劃分形式與網格數量等因素對計算結果的影響，確定合理的網格劃分方法，提高計算的準確性。之后，對一艘3 000 m深水鉆井船進行計算，分析月池形狀與航速等方面對鉆井船阻力的影響，有較好的實際應用前景。

深海鉆井船；月池；阻力；數值模擬

引　言

隨著陸地油氣資源的消耗，人們的目光逐漸從陸地轉向海洋。開發海洋油氣資源，需要進行勘探、鉆井、生產與運輸等作業，其中鉆井船是海洋油氣鉆井作業的必要裝備之一。鉆井船是浮船式海上鉆井平臺，航行方式主要有自航與拖航兩種，可以裝配多種鉆井作業所需的設備及器具。與常規船型不同的是，鉆井船一般在船中附近會有一個較大的垂向貫通式開口，這種結構被稱為月池結構，其會對鉆井船的結構、運動與遷移自航阻力等方面產生諸多不利的影響［1-5］。就航行阻力而言，有月池時的阻力會明顯大于無月池時的阻力。本文對一艘具有遷移自航能力的鉆井船進行了關于航行阻力的數值模擬研究，試圖構建鉆井船阻力的數值預報方法，探討月池及其構型對鉆井船自航阻力與相關特性的影響。

1　理論基礎

本文基于CFD技術，采用FLUENT軟件對鉆井船的阻力開展數值模擬研究。

1.1 流體力學控制方程

流體在流動的過程中，需要遵守守恒定律，如質量守恒定律、動量守恒定律與能量守恒定律，本節主要對模擬過程中涉及到的質量守恒方程與動量守恒方程進行介紹。

質量守恒方程的物理意義可以表述為：在無源無匯的情況下，單位時間內流體微團的質量改變量，等于單位時間流入或流出微團的流體質量。

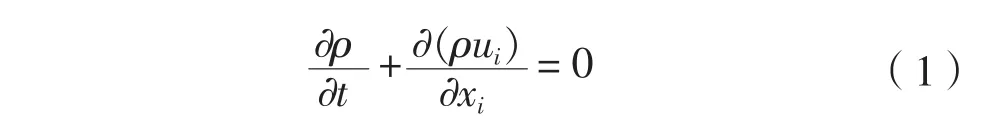
在定常不可壓縮流動中可以表示為：

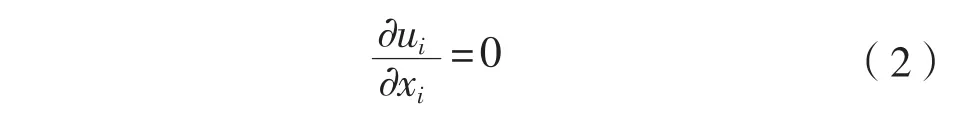
RANS方程為：

式（1）— 式（3）中：ρ為流體密度，kg/m3；t為時間，s；u為流體速度，m/s；μ為流體動力粘性系數，N·S/m2；P為壓力，N。

1.2 VOF法

VOF法是一種追蹤自由表面的方法，由Hirt 與Nichols在20世紀70年代提出。該方法是通過引入一個流體體積方程，結合其他的基本方程，獲得捕捉自由液面的新方法。其可有效跟蹤復雜的自由液面，并占用較小的內存，能夠應用到三維流體計算中。VOF法主要思路是：定義一個標量函數f，充滿該種液體時的f值為1，充滿另一種液體時的f值為0。在各個單元上對f積分再除以單元體積，得到單元中液體所占據的比例F。通過F便可確定自由液面發現方向、形狀與近似位置。自由液面問題最終就變成求解計算域內F的問題。

2　鉆井船阻力CFD模擬及驗證

2.1 計算模型

本節計算的鉆井船船模的主要參數：總長L = 8.504 m；型寬B = 1.567 m；吃水T = 0.317 m，遷移航速為V = 1.192 m / s（2.318 kn），縮尺比為26.8。參見圖1。

圖1　鉆井船幾何模型

該鉆井船的月池長1.432 m、寬0.465 m。月池內有一個臺階，臺階長0.440 m、高0.272 m。計算時，臺階的高度分別取0.241 m、0.272 m與0.304 m。月池結構的縱剖面圖見下頁圖2。

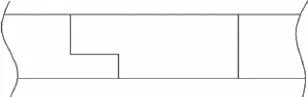
圖2　月池結構

由船模航速1.192 m / s（2.318 kn），通過相似換算的方法求得對應實尺度船舶12 kn時的設計航速（自航遷移航速）。

2.2 邊界條件的設定

參考相關文獻［6］，將計算域沿船首方向取1倍船長、船尾方向取3倍船長。鉆井船附近取一個小域作為內域，采用對稱模型（以船模的中縱剖面為對稱面），入口為速度入口、出口為自由出流，船體表面為無滑移壁面條件。具體的計算域劃分形式見圖3。

圖3　計算域劃分

2.3 網格劃分

在CFD模擬的過程中，經常會遇到運動邊界與邊界形狀發生變化的情況，此時常規的計算方法已無法滿足需求，在這樣的背景之下，動網格技術應運而生。一般來說，運動邊界問題主要有兩種：一種是預先指定的運動，即運動邊界以某一確定的運動規律進行運動，如已知速度（角速度）或者是加速度（角加速度）等情況；另一種是非預先指定的運動，即物體后續的運動規律由當前的時間步長所受的力或者是力矩來確定。

由于需要考慮浮態（縱傾與升沉）對鉆井船阻力的影響，因此需要使用動網格技術。本文使用混合網格的劃分方法，在內域范圍內使用非結構網格，外域則采用結構網格劃分，并在鉆井船周圍布置邊界層網格。內域網格隨鉆井船一起運動，外域網格發生形變。由于外域網格尺寸較大，在發生小幅度變形時并不會使網格發生較大的曲率變化。為更好地確定網格數目，本文將網格逐漸加密，從65萬到170萬（計算機計算能力上限），以此來探尋合理的網格數量。計算結果見表1與圖4。

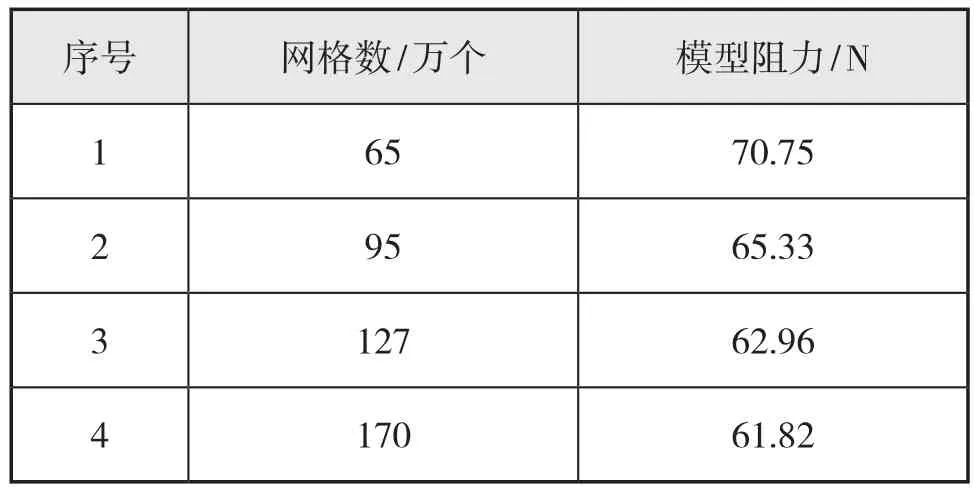
表1　模型阻力

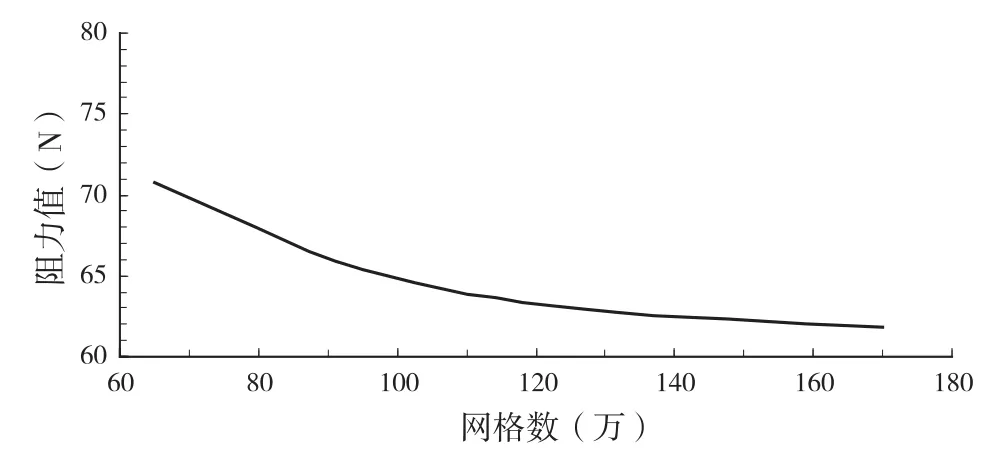
圖4　網格數對阻力值影響趨勢

由表1結果以及圖4可以看出，阻力值隨網格數目的增加而趨于穩定。從計算的角度進行分析，網格數太少會使計算結果不準確，而網格數太多又會增加計算成本，并且收斂不易，因此，本文選擇140萬網格數進行計算，并對鉆井船附近與水線面附近的網格進行局部加密。

2.4 結果與分析

參考Son H J、Choi S H、Kim M H等人［7］的水池模型實驗結果，再與本文模擬的結果進行對比，結果列于下頁表2。

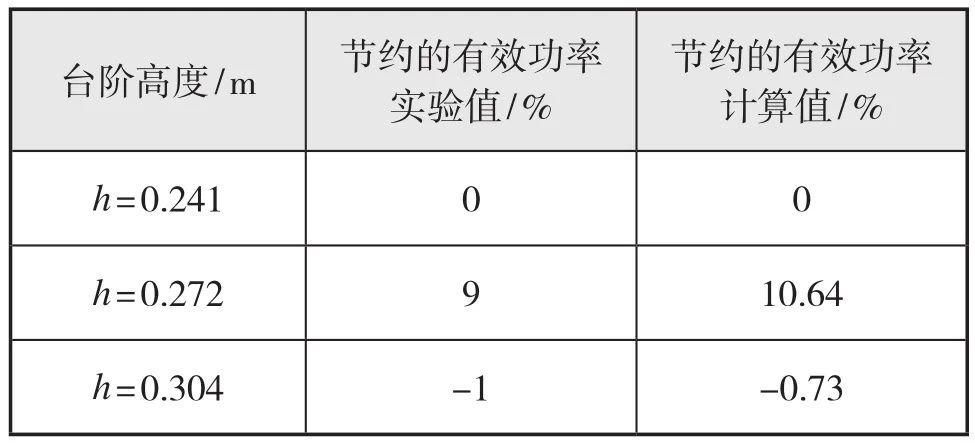
表2　計算值與實驗值對比

表2表明：當月池內的臺階高度為0.304 m時，鉆井船可以節約更多的有效功率。臺階高度為0.241 m時，鉆井船阻力會較臺階高度0.272 m時有小幅度提升，數值計算求得的結果與水池實驗的結果相近。鉆井船阻力隨臺階高度變化的趨勢與實驗相比基本一致，提高了模擬鉆井船的準確性。

3　算例船阻力計算與分析

3.1 航速與月池尺寸參數

與其他類型的船舶相比，鉆井船有一個垂向貫通且與海水相連的月池結構，該結構對鉆井船的阻力性能有很大影響［8-9］。因此，研究鉆井船月池的形狀與航速對阻力的影響，可以為鉆井船月池的設計與鉆井船遷移速度的選擇提供一定的參考。

為研究不同月池形狀與航速對鉆井船阻力的影響，特選取四種船舶（分別擁有長方形月池、方形月池、圓形月池以及無月池），然后分別在10 kn、12 kn與14 kn的航速下行駛，再對比分析CFD模擬的數據并得到結論。

本論文計算的模型是縮尺后的模型（縮尺比λ = 26.8）。總長為8.877 m、垂線間長為8.579 m、型寬為1.567 m、型深為0.727 m、吃水為0.317 m、方形系數為0.846、水線面系數為0.917、船中橫剖面系數為0.992、月池尺寸為0.932 m×0.470 m（長×寬）。算例船的橫剖面線型如圖5所示。

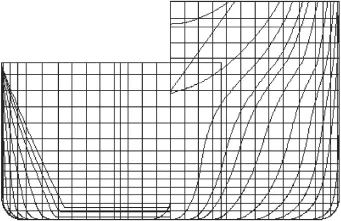
圖5　計算模型橫剖面圖

為保證模擬計算精度，需要確保船模與實際的鉆井船周圍流動的相似，即保證雷諾數（Re）與傅汝德數（Fr）相等，但是這樣的流動對于實際數值模擬是難以實現的，因此只能保證部分相似，即傅汝德數相等。根據這一思路，對模擬過程中的速度進行換算，結果如表3所示。

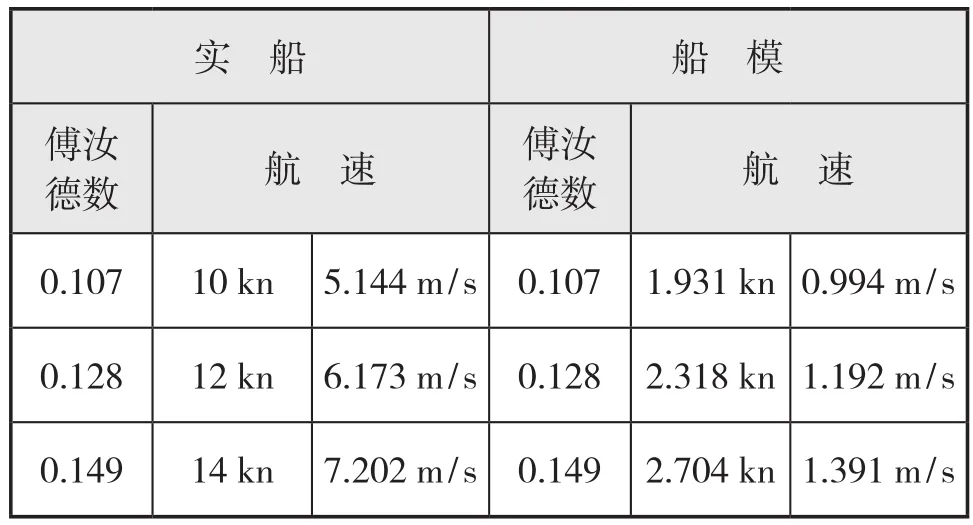
表3　模型與實船航速

以計算鉆井船原有的矩形月池為基準，通過等面積的原則，選取正方形與圓形的月池尺寸如表4。

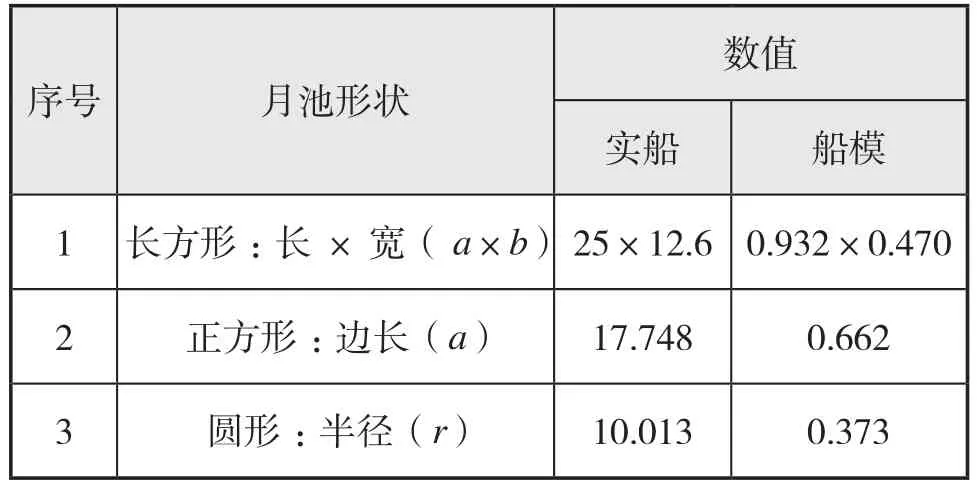
表4　月池形狀與尺寸　m

計算域與網格的劃分參考上一小節的方法。入口選擇為速度入口，并將其分為兩個部分：一個是空氣速度入口，另一個是水的速度入口。速度設定為定值，即來流為均勻來流。出口選擇自由出流，船舶的中縱剖面所在的平面設定為對稱邊界條件，在對稱面上沒有物理量的交換，即對稱面上的法向速度為0。鉆井船表面設定為無滑移壁面邊界條件，底部邊界也設定為無滑移壁面邊界條件，并且以速度入口處相同的速度進行平移運動，其他邊界設定為滑移壁面邊界條件。

3.2 計算結果與分析

通過式（4）求得因月池的存在而導致的鉆井船附加阻力。

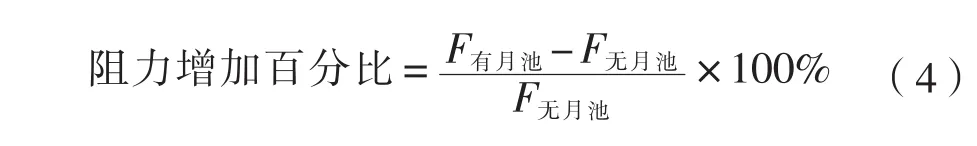
對計算結果進行整理，得到數值計算的模型阻力結果，見表5、表6與圖6。

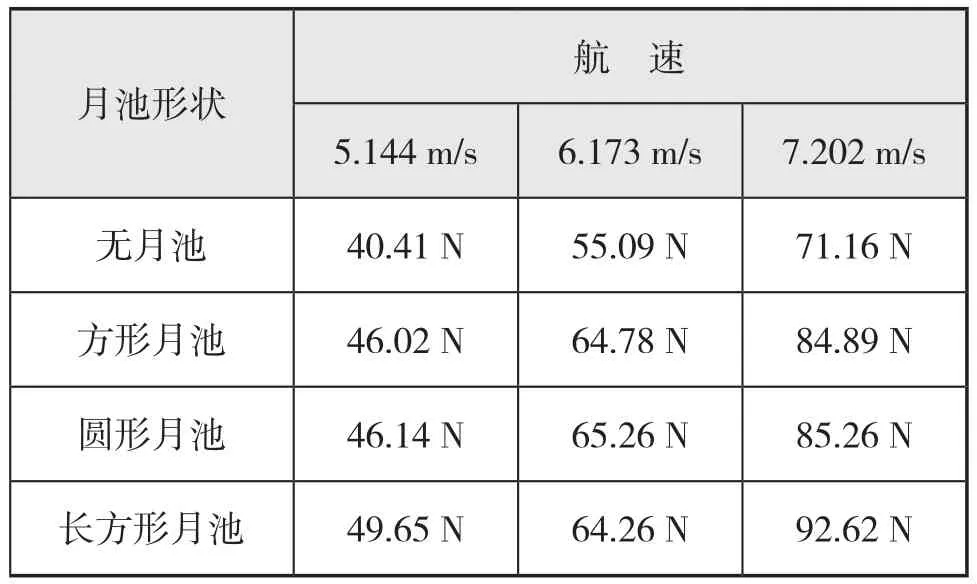
表5　不同航速下的鉆井船阻力計算值

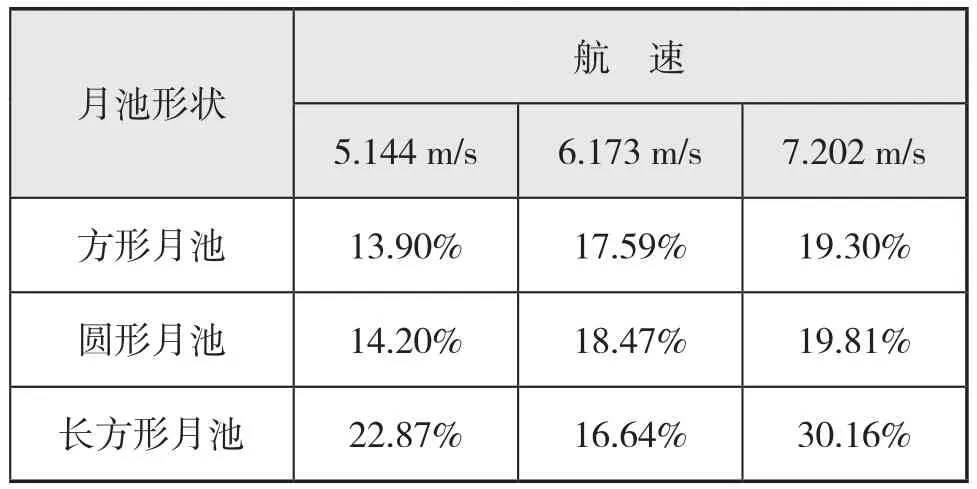
表6　不同航速下的鉆井船阻力增加百分比

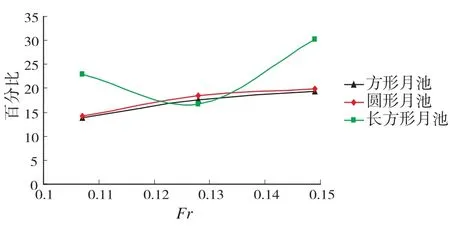
圖6　月池的阻力增加百分比

與無月池的船舶相比，加裝月池的鉆井船阻力明顯升高。安裝圓形月池與方形月池的鉆井船阻力增加百分比隨著航速的提升而增加。長方形月池在航速為5.144 m/s時，阻力增加百分比較高（為22.87%）；隨著航速的提高，當航速為6.173 m/s時，阻力增加百分比有一定程度的降低（為16.64%），之后，在航速繼續提升的過程中，阻力增加百分比再次升高。

月池內流體的運動方式可以分為活塞運動與晃蕩運動。活塞運動比較規律，晃蕩運動則較為復雜，可以分為一階乃至高階的晃蕩運動。由Faltinsen［2，10，11］與福田等人［1］的研究，獲得鉆井船模型月池流體活塞運動與晃蕩運動的固有頻率的經驗公式。

活塞運動的公式為：

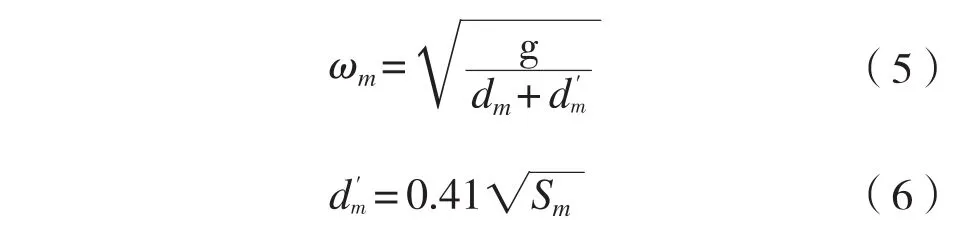
式中：dm為吃水，m；g為重力加速度，m/s2；Sm為月池的橫截面積，m2；為考慮附加質量對流體振蕩的影響時引入的一個附加吃水，m。

晃蕩運動的公式為：

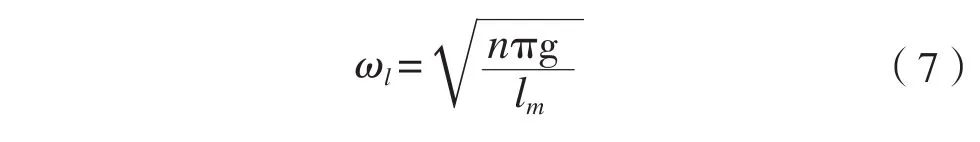
式中：n為頻率的階數（例如：當n = 1時，求得晃蕩運動的一階固有頻率）；lm為月池的長度，m。

由上式得到月池內流體活塞運動與一階晃蕩運動的固有頻率，見下頁表7。

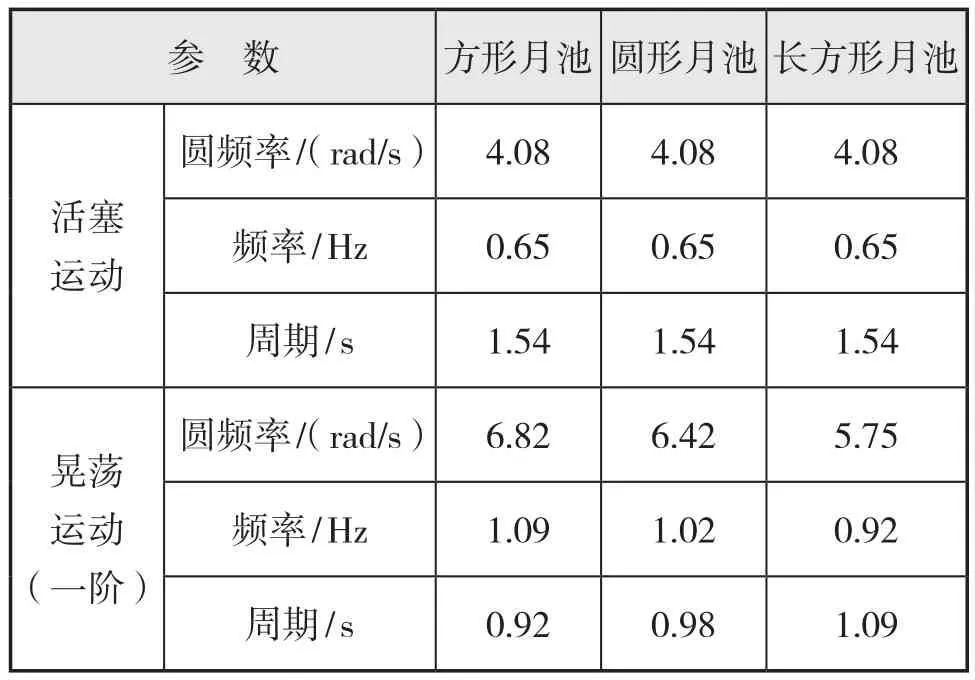
表7　月池活塞運動與晃蕩運動的固有頻率和周期（模型）

在計算穩定后（Fr = 0.149），得到阻力振蕩的頻率，見表8。

表7與表8表明，圓形月池與方形月池阻力的振蕩周期與活塞運動的固有頻率十分接近，長方形月池與固有頻率下差較大。

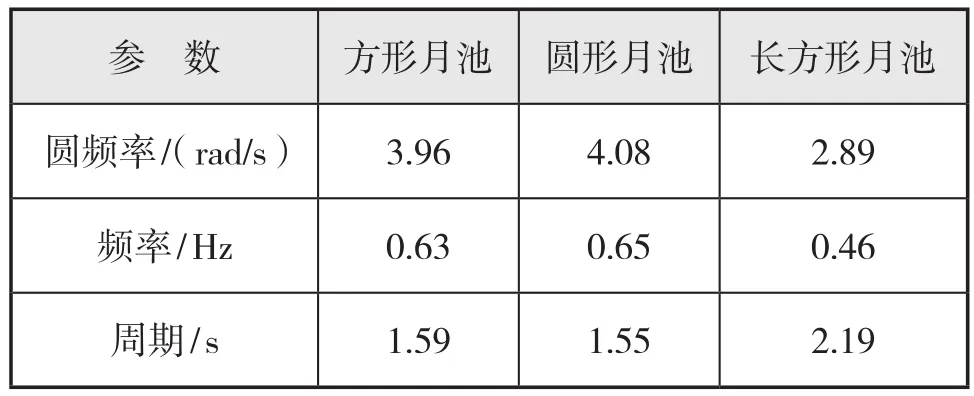
表8　鉆井船阻力振蕩頻率與周期（模型）

為進一步觀察月池內流體運動的情況，以方形月池為例，截取鉆井船的中縱剖面，選取其在固定時刻t = 45時，不同航速下圓形月池內的流體在不同時刻的速度矢量圖。

圖7表明，隨著航速的提升，月池內流體的振蕩幅度逐漸增加，月池內的漩渦也越來越明顯。

圖7　方形月池內流體速度矢量圖

綜合圖6、圖7及表5 — 表8的數據分析如下：圓形月池與方形月池的阻力隨航速的提升而增大。隨著航速的提升，月池前沿處漩渦產生與脫落的速度逐漸加快，漩渦的運動引起并加劇月池內流體的運動，并且漩渦運動的頻率逐漸接近固有活塞運動的頻率，導致運動的加劇。從能量的觀點進行分析，月池內流體運動與漩渦形成的能量均是由鉆井船提供的，隨著航速的提升內流體振蕩與漩渦的運動越來越劇烈，所以方形月池與圓形月池的附加阻力也越來越大。

長方形月池一階晃蕩運動與活塞運動的固有頻率較為接近，使流體同時受到這兩種固有頻率的影響，所以長方形月池的附加阻力隨著航速先降低，然后繼續升高。

4　結　論

本文對比了當傅汝德數分別為0.107、0.128與0.149時對應的三種航速（5.144 m/s、6.173 m/s與7.202 m/s）下，安裝有等面積的方形、圓形與長方形三種形狀月池的鉆井船阻力，結果表明：

（1）與Son H J、Choi S H、Kim M H等人的船模水池實驗結果相近，表明CFD數值模擬的方法可以作為預測鉆井船阻力的重要方法。

（2）裝有方形月池或圓形月池的鉆井船其阻力隨航速的提升而增加；裝有長方形月池的鉆井船，其阻力在航速為6.173 m/s時有較小幅度降低，之后，在航速為7.202 m/s時繼續升高。因此，在實際鉆井船設計的過程中，可以通過設定合理的航速來減小裝有長方形月池鉆井船的阻力。

（3）從能量的觀點進行分析，月池內流體運動與漩渦形成的能量均由鉆井船提供，隨著流體振蕩與漩渦的運動越來越劇烈，月池產生的附加阻力也越來越大。

（4）月池內漩渦產生與脫落的速度隨航速的提高而加快，漩渦的運動會帶動月池內流體的運動。當運動頻率與活塞運動或者晃蕩運動的固有頻率接近時，該運動現象尤為明顯，附加阻力也變得更大。

（5）月池內流體活塞運動與晃蕩運動的固有頻率與月池的固有屬性有關。因此在滿足鉆井裝備及保障設備與作業器具等布置的前提下，可以通過合理設定月池尺寸以減小附加阻力。

［ 1 ］ Fukda K. Behavior of water in vertical well with bottom opening of ship and its effect on ship motions ［J］. Journal of the Society of Naval Architects of Japan， 1977（141）：107-122.

［ 2 ］ Faltinsen O M. Sea loads on ships and offshore structures ［M］. Cambridge University Press，1990.

［ 3 ］ Van’t Veer R， Tholen H J. Added Resistance of Moonpools in Calm Water［C］ // Proc. of OMAE’08，27th International Conference on Offshore Mechanics and Arctic Engineering. Portugal： OMAE， 2008：153-162.

［ 4 ］ Gaillarde G， Cotteleer A. Water Motion in Moonpools Empirical and Theoretical Approach［C］ //Association Technique Maritime et Aeronautique， France： ATMA ，2004.

［ 5 ］ Hammargren E， T?rnblom J. Effect of the Moonpool on the Total Resistance of a Drillship［D］. Sweden： Chalmers University of Technology，2012：11-22.

［ 6 ］ 鄧銳， 黃德波， 于雷，等. 影響雙體船阻力計算的流場CFD因素探討［J］. 哈爾濱工程大學學報，2011 （2）：141-147.

［ 7 ］ Son H J， Choi S H， Kim M H， et al. Drag Reduction of Recess Type Moonpool Under Vessel’s Forward Speed ［C］ // Proc. of OMAE’08，27th International Conference on Offshore Mechanics and Arctic Engineering. Portugal：OMAE， 2008：143-148.

［ 8 ］ 張曉宇，胡開業，周雯雯.帶月池深海鉆井船搖蕩運動性能分析［J］.船舶，2016（1）：29-36.

［ 9 ］ 李志雨，張海彬.基于CFD的鉆井船月池流場及附加阻力研究［J］.船舶，2015（4）：10-15.

［10］ Faltinsen O M，Rognebakke A N. Two-dimensional Resonant Piston-like Sloshing in a Moonpool［J］. Journal of Fluid Mechanics， 2007（9）： 359-397.

［11］ Fredriksen A G，Kristiansen T， Faltinsen O M. Experimental and numerical Investigation of wave resonance in moonpools at low forward speed［J］. Applied Ocean Research，2014（9）： 28-46.

Infl uence of moonpool structure on resistance of drilling ship

ZHANG Xiao-yu1HU Kai-ye2JI Yuan2ZHOU Wen-wen2
(1. Ocean Engineering Equipment Research Institute, CNPC Bohai Equipment Research Institute, Panjin 124010, China;
2. College of Shipbuilding Engineering, Harbin Engineering University, Harbin 150001, China)

Based on the navigation engineering background of drilling ships, the present study focuses on the calculation and analysis of the calm water resistance of a drilling ship with the detailed experimental data by using viscous computational fluid dynamics with the consideration of the influence of floating state on the resistance. The reasonable meshing topology is determined to improve the calculation accuracy by analyzing the influence of the meshing topology and the grid number on the calculation results. Then, a 3 000-meter deep water drilling ship is calculated to analyze the resistance performance under the different moonpool shapes and speeds. The conclusion would have a better practical application prospect.

deepwater drilling ship; moonpool; resistance; numerical simulation

U674.38+1

A

1001-9855（2016）04-0014-07

10.19423 / j.cnki.31-1561 / u.2016.04.014

中國石油天然氣集團公司攻關課題（2011B-1064）。

2015-12-25；

2016-03-10

張曉宇（1972-），男，碩士，高級工程師，研究方向：海工裝備。

胡開業（1980-），男，博士，講師，研究方向：水動力性能分析。

紀 元（1990-），男，碩士，研究方向：海洋工程水動力性能。

周雯雯（1989-），女，碩士，研究方向：海洋工程水動力性能。