水下滑翔器運動仿真與控制器設計*

鐘曉鋒

(海裝西安局　西安　710075)

ZHONG Xiaofeng

(Xi’an Military Representatives Branch of Navy Equipment Department , Xi’an　710075)

?

水下滑翔器運動仿真與控制器設計*

鐘曉鋒

(海裝西安局西安710075)

水下滑翔器是一種無外掛推進系統，僅依靠內置執行機構調整重心位置和凈浮力來控制其自身運動的新型水下機器人，主要用于長時間、大范圍的海洋環境監測。文中分析了水下滑翔器的流體動力情況，建立了其數學模型。針對水下滑翔器俯仰通道開環性能較差的缺點，設計了PID控制器。仿真表明，該控制器性能穩定，可使水下滑翔器的航行性能極大提高。文中同時對不同浮力情況下的水下滑翔器水平速度進行了仿真分析。這些工作，為設計水下滑翔器奠定了基礎。

水下滑翔器; PID控制; 流體動力

ZHONG Xiaofeng

(Xi’an Military Representatives Branch of Navy Equipment Department , Xi’an710075)

Class NumberTG156

1　引言

水下滑翔器(AUG)是一種將浮標技術與水下機器人技術相結合、依靠自身浮力驅動，沿鋸齒型航跡航行的新型水下機器人系統[3]。它采用內置的姿態調整機構和無外掛的驅動裝置，減少了載體的外置裝置，避免了對載體線型的破壞，大大改善了系統的水動力特性，因而具有制造成本和維護費用低、可重復利用、投放回收方便、續航能力強的特點，適宜大量布放，在海洋環境的監測、調查、探測等方面具有廣闊的應用前景。

國內針對水下滑翔器的理論研究，集中于對其穩態情況的計算和分析[2～3,5]。這種方法的優點是能夠較為迅速地估算系統的大體性能，但無法對水下滑翔器這樣一個系統進行仿真模擬，從而無法進一步了解其運動特點，更無法設計閉環控制器。

在文中，通過對水下滑翔器模型的動態仿真可以看到，對于水下滑翔器來說，通過調整其重心位置和自身浮力來改變航行姿態和速度是可行的。但在開環控制的情況下，輸出響應屬于衰減振蕩過程，調節時間過長，在調節過程中受到較大的外部擾動，容易出現失控；而且調節過程振蕩較大，不利于搭載儀器設備的正常工作。

因此，需要設計一種閉環控制器，可以任意設定水下滑翔器的航行姿態，并且達到較快收斂的效果，這樣，不僅有利于滑翔器的穩定，而且有利于搭載實驗設備的工作。

2　水下滑翔器數學模型

2.1坐標系定義

為了描述水下機器人的運動，定義兩個坐標系，即載體坐標系(以載體浮心為原點)和地面坐標系(慣性坐標系)[7]，如圖1所示。

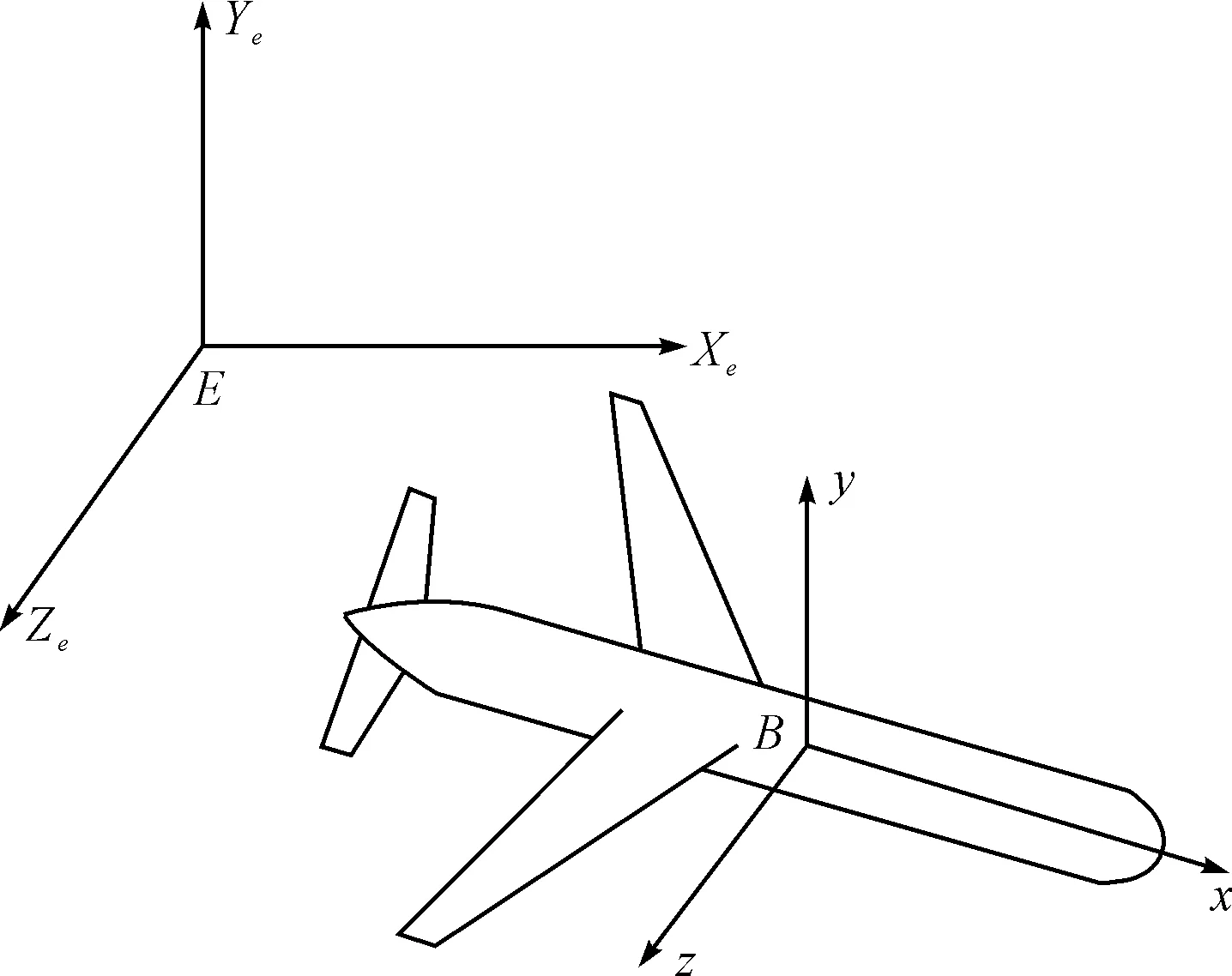
圖1　水下滑翔器坐標系

地面坐標系又稱靜坐標系，它是與地面固連在一起的。地面系的原點E可選在地面某一點，例如發射點。EXe軸在水平面內，指向發射方向為正。EYe軸在垂直面內，垂直向上為正。EZe軸垂直EXeYe平面，其正方向使EXeYeZe構成右手直角坐標系。

體坐標系又稱動坐標系，它與glider固連在一起。體坐標系的原點選在glider的浮心B處。Bx軸沿glider縱軸，指向前為正。By軸垂直于Bx軸，當glider在地面上水平放置時，指向上為正。Bz垂直Bxy平面，其正向使Bxyz構成右手系。

glider相對地面系的位置，可用體坐標系原點在地面系的坐標分量Xe，Ye，Ze來確定。glider相對于地面系的姿態可用體坐標系與地面系之間的三個歐拉角，即橫滾角φ，俯仰角θ和航向角ψ來確定。三個歐拉角的定義如下：

偏航角ψ：glider縱軸Bx在水平面(EXeZe)內的投影與地軸EXe(雷發射方向)之間的夾角，glider左偏為正(叢雷尾朝雷頭發射方向看)。

俯仰角θ：glider縱軸Bx與水平面(EXeZe)的夾角，glider抬頭為正。

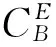
2.2水下滑翔器數學模型

在模型中的力(力矩)，如無特殊說明，均為體坐標中建立。各個符號意義如下：

i,j,k為體坐標系三個坐標軸方向的單位矢量；u，v，w為體坐標系三個線速度；p，q，r為體坐標系三個角速度；VG為質心的絕對速度；VT為體坐標系牽連速度；RG=xGi+yGj+zGk為重心位置矢量；Ω=pi+qj+rk為浮心轉動矢量；LG=JxGpi+JyGqj+JzGrk為質心動量矩；M為外力對浮心的力矩；MG為外力對質心的力矩；JxG、JyG、JzG為Bx、By、Bz軸的轉動慣量；α,β為攻角和側滑角；M為glider質量。

2.2.1空間運動受力(力矩)

1) 粘性類流體動力

與粘性類流體動力相關的力和力矩包括縱向力、垂向力、橫向力、橫滾力矩、偏航力矩和俯仰力矩。在對glider建模時，由于其運動速度較小，因此可以僅對阻力系數取二次項，其他流體粘性類動力系數均按線性處理。

X(縱向力)、Y(垂向力)、Z(側向力)——流體動力主向量在體坐標系BX、BY、BZ軸方向的投影。

R(橫滾力矩)、M(偏航力矩)、N(俯仰力矩)——流體動力矩在體坐標系BX、BY、BZ軸方向的分量。

2) 慣性類流體動力

慣性類流體動力與物體運動的加速度、角加速度成線性關系。glider空間六個自由度運動所有的慣性力共有36項，即

勢流理論已經證明，λij=λji(i,j=1,2,…,6)，因此36個系數中只有21個是獨立的，并統稱附加質量，又稱加速度系數。附加質量產生的機理是當glider在水中作加速運動時，帶動周圍的一部分水也作加速運動，根據作用與反作用原理，周圍的水對glider就產生反作用，即“附加質量力”，它的方向總是與運動方向相反[8]。

附加質量對于選定的坐標系而言，只取決于glider表面的幾何形狀，而與運動參數無關。由于glider相對于體坐標系Bxy平面式對稱的，而相對于Bxz平面在通常情況下，上、下鰭的不對稱性也是很小的，忽略這種不對稱性，而視glider具有兩個對稱面，這樣不為零的λij只有10個，即λ11,λ22,λ26,λ33,λ35,λ44,λ53,λ55,λ62,λ66，且λ62=λ26，λ53=λ35，λ35=-λ26。

(1)

3) 浮力

glider的負浮力記為B，在地面系中：B=BYe，其中Ye表示地面系EYe軸方向上的單位矢量。

根據地面系到體坐標系的轉換矩陣式有

(2)

4)重力和重力矩

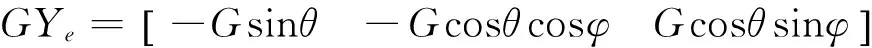
RG×G=GRG×Ye由

(3)

2.2.2動力學方程

1)速度方程

VG=VT+Ω×RG

2)動量方程

(4)

其中：

式中，F代表作用于glider上的所有外力之和。

3)動量矩方程

根據剛體的動量矩定理，在地面系中，glider對質心的動量矩隨時間的變化率等于外力對質心力矩之和：

(5)

式中

由剛體的轉動定律知，glider對質心G的動量矩可表示為

LG=JxGpi+JyGqj+JzGrk

2.2.3空間運動方程

綜上，glider的空間運動方程包括如下：

-m[vr-wq+xG(q2+r2)-p(yGq+zGr)]

=-(G-B)sinθ+X

(6)

-m[wp-ur+yG(r2+p2)-q(zGr+xGp)]

=-(G-B)cosθcosφ+Y

(7)

-m[uq-vp+zG(p2+q2)-r(xGp+yGq)]

=(G-B)cosθsinφ+Z

(8)

-[(Jy-Jz)qr+myG(up-vq)+mzG(ur-wp)]

=Gcosθ(yGsinφ+zGcosφ)+R

(9)

-[(Jy-Jx)rp+mzG(vr-wq)+mxG(vp-uq)]

=-G(zGsinθ+xGcosθsinφ)+M

(10)

-[(Jx-Jy)pq+mxG(wp-ur)+myG(wq-vr)]

=G(-xGcosθcosφ+yGsinθ)+N

(11)

(12)

(13)

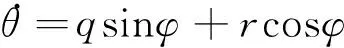
(14)

+w(sinψcosφ+sinθcosψsinφ)

(15)

(16)

+w(cosψcosφ-sinθsinψsinφ)

(17)

(18)

α=arctg(-v/u)

(19)

β=arcsin(w/VT)

(20)

在以上15個方程中，未知數為u,v,w,p,q,r,φ,ψ,θ,XE,YE,ZE,VT,α,β共15個參數，方程可解。

2.3姿態調節方式

glider的深度變化通過調節重心縱移量和浮力來實現；其回旋可通過調節重心側移或者通過直舵調節來實現。不論哪一種方式，為保證滑翔器穩定，都應使重心相對浮心有一個下移量。

在本文中，采用重心縱移量xG和舵角δ為控制量，這樣整個系統就成為一個非線性系統。方程中涉及的流體動力(力矩)按照如下公式計算：

X=Lsinα-Dcosα

(21)

Y=Lcosα+Dsinα

(22)

其中

D=(KD0+KDaα2+KDbβ2)V2

(23)

L=KLαV2+KLrrV

(24)

Z=(KZβ+KZδδ)V2+KZqqV

(25)

R=KRpV

(26)

M=(KMβ+KMδδ)V2+KMqqV

(27)

N=KNαV2+KNrrV

式中，攻角(或側滑角)與速度平方項乘積的系數分別為升力(力矩)、阻力(力矩)或側向力(力矩)系數；角速度與線速度乘積項的系數為阻尼系數。

3　開環仿真情況

3.1模型參數

按照表1中參數進行仿真。

表1　模型參數

續表1

項目符號數值單位升力系數KL350N(s/m)2升力阻尼系數KLr45N(s/m)2側向力系數KZ-100N(s/m)2KZδ-40N(s/m)2側向力阻尼系數KZq-70N(s/m)2橫滾阻尼系數KR-18kg/m航向力矩系數KM-25kg/mKMδ-30kg/m航向阻尼系數KMq-70kg/m俯仰力矩系數KN-25kg/m俯仰阻尼系數KNr-65kg/m

3.2垂直面開環響應

此時，glider無側滑角、橫滾角。因此，一切側向力和力矩均為零。在滑翔器模型中，令φ,ψ,p,q,w均等于零，得到垂直面模型：

=-(G-B)sinθ+Lsinα-Dcosα

(28)

=-(G-B)cosθ+Lcosα+Dsinα

(29)

(30)

(31)

(32)

(33)

(34)

α=arctan(-v/u)

(35)

對重心縱移量yG一個階躍輸入，得到垂直面的開環響應如圖2所示。

圖2　滑翔器垂直面開環響應

從圖2中可以看出，UUV的開環響應是一條振蕩衰減的曲線，其衰減速度很緩慢，需要設計一個快速穩定的控制器。

4　控制器設計

4.1控制器參數選取和注意事項

俯仰通道采用PID控制器。在連續系統中，PID系數分別為：0.02,0.004,0.2，當利用計算機進行離散采樣控制時，可根據采樣時間，對PID系數進行相應變換處理即可，如圖3所示。

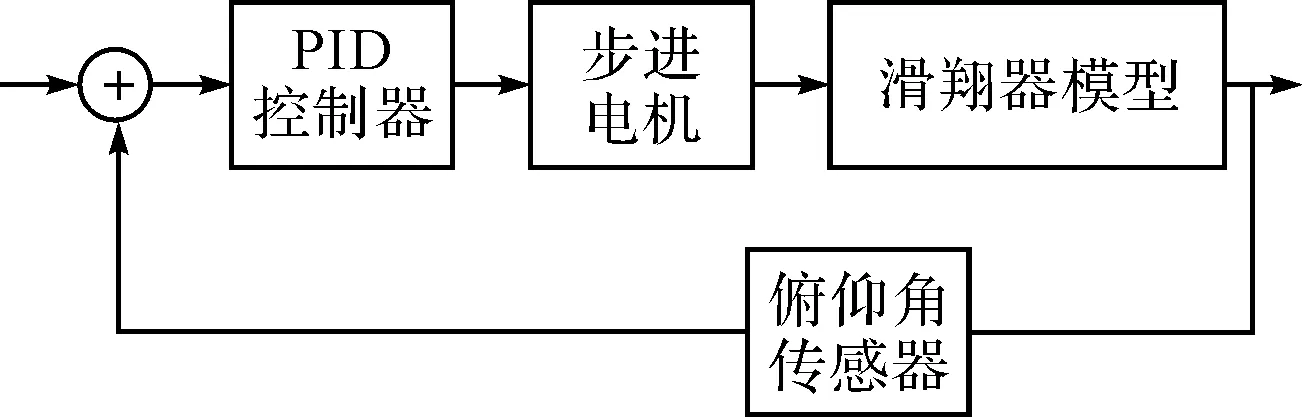
圖3　垂直面閉環控制示意圖

由于無動力UUV需要長時間滑翔和工作，因此，節約能源成為控制系統的一個重要任務。因此節約能源意味著更遠的航程和更長的工作時間[9]。根據這一原則，在控制系統中采用如下方法：

1)在滿足系統性能的條件下，盡量增大控制周期(例如采用1Hz)，控制器發出相關控制指令后，無關元器件進入休眠狀態，等待下一次控制周期到來時再被激活。

2)采用帶有自鎖功能的步進電機和舵機，到達指定位置后，可以利用電機的自鎖功能，切斷電源，保持位置，這就避免了電機的高頻振蕩，從而節省了電能。

3)控制器的設計中加入滯環環節。即對姿態的控制，并不需要很高精度，在某一個誤差范圍內(例如2deg)，則不對執行機構下達指令。這樣，雖然控制精度稍有下降(僅僅2deg)，但使得在一個UUV的下潛或上浮周期中，耗費的能量大為減少[10]。

4.2閉環仿真結果

圖4　閉環控制俯仰角響應

可以看到，閉環控制的俯仰角響應速度快，而且無振蕩，可以滿足控制要求。

通過分析攻角與俯仰角的關系可以看出，攻角與俯仰角絕對值呈單調遞增關系。在俯仰角絕對值小于10deg的情況下，攻角穩態值小于3deg。

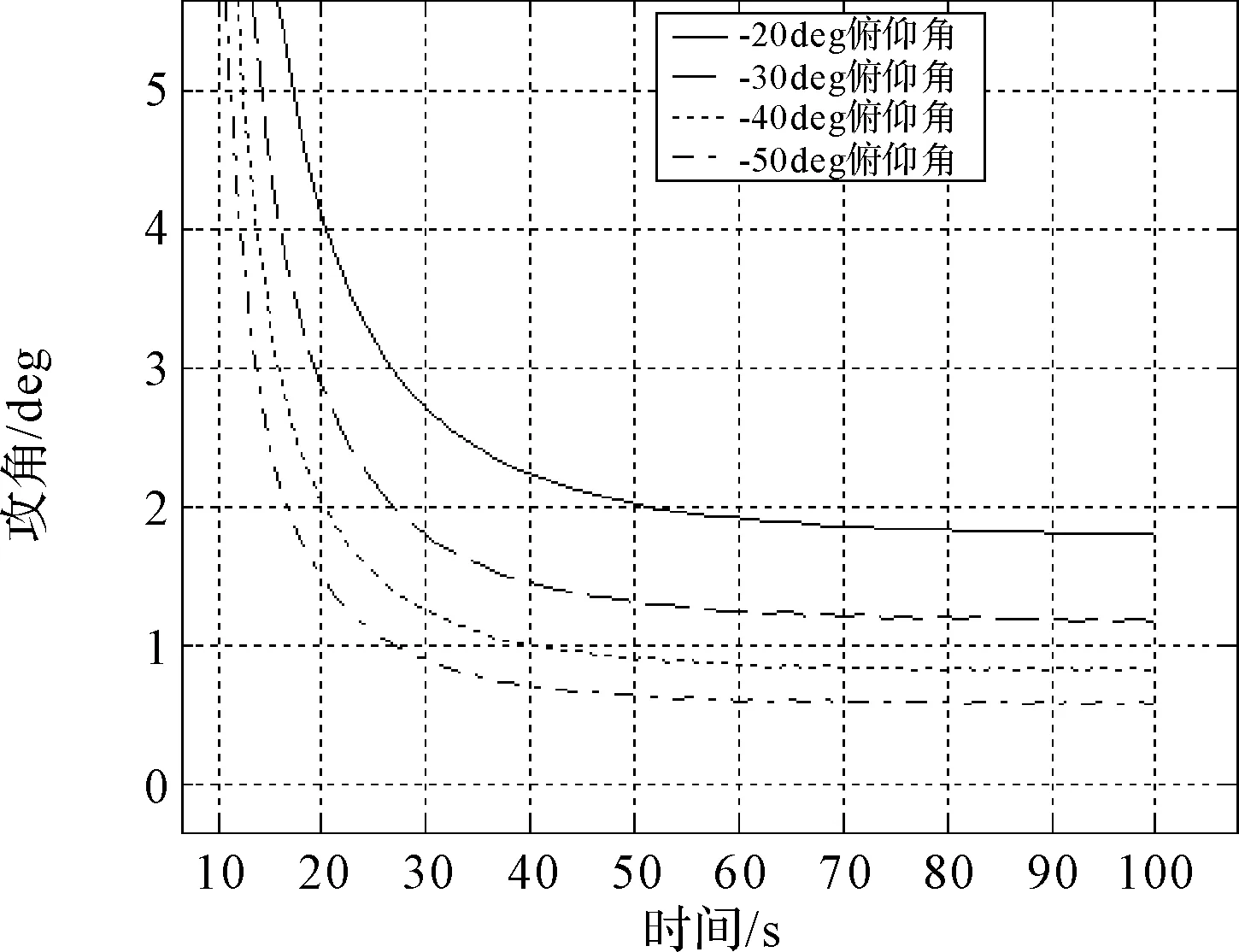
圖5　閉環控制攻角角響應

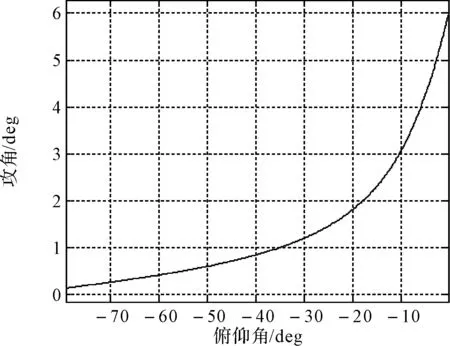
圖6　穩態情況下俯仰角與攻角關系圖

圖7　-30deg俯仰角、5deg舵角情況下三維運動圖

圖8說明負浮力的增加可以導致滑翔器水平速度增加。不同負浮力情況下，最大水平速度大約發生在俯仰角-35deg附近。

圖8　不同負浮力情況下水平速度與俯仰角關系圖

5　結語

本文對水下滑翔器的運動機理進行了分析，建立了數學模型，利用數學仿真的方法對滑翔器的運動特性作了詳細的研究。針對滑翔器開環控制性能較差的特點，設計了控制器。通過開環、閉環仿真對比，可以看到：優化設計的PID控制器可以滿足快速響應的要求，通過減小滑翔器自身的超調和振蕩，有利于搭載儀器的正常工作。同時，文中也通過仿真對比了不同負浮力和俯仰角條件下，滑翔器在穩態時水平速度的變化情況。

[1] D. C. Webb, P. J. Simonetti, and C. P. Jones. SLOCUM: An underwater glider propelled by environmental energy[J]. IEEE Journal of Oceanic Engineering,2001,26(4):447-452.

[2] 王樹新.水下滑翔器的運動建模與分析[J].海洋技術，2005(3):5-9.

[3] 吳利紅，俞建成，封錫盛.水下滑翔機器人水動力研究與運動分析[J].船舶工程，2006(1):12-16.

[4] N.E. Leonard and J. Graver. Model-based feedback control of autonomous underwater gliders[J]. IEEE Journal of Oceanic Engineering, 2001,26(4):633-645.

[5] 張奇峰，俞建成.水下滑翔機器人運動分析與載體設計 [J].海洋工程，2006(2):74-78.

[6] 張宇文.魚雷彈道與彈道設計[M].西安：西北工業大學出版社，1999：35-37.

[7] 蔣新松.水下機器人[M].沈陽：遼寧科學技術出版社，2000：12-15.

[8] 余立中.我國的海洋剖面探測浮標-COPEX[J].海洋技術，2003(5):15-18.

[9] 趙進平.發展海洋檢測技術的思考與實踐[M].北京：海洋出版社，2005：66-67.

[10] 王兵振.水下滑翔器定常直線滑翔運動穩定性分析[J].海洋技術，2009(2)：2-3.

Simulation and Controller Design of Autonomous Underwater Glider*

Autonomous underwater glider(AUG) is a new kind of underwater vehicle without any external active propulsion, velying on internal actuator to adjust the center of gravity and the net buoyancy to generate its motion. With advantages of long range, long duration and cost-efficiency, it can be used to explore ocean environments for a long time and covering a large area. Mathematical model is build based on the analysis of hydrodynamic on AUG. Aiming at the disadvantages of poor open-loop performance of pitch channel, the PID controller is designed Simulation shows that the controller has an outstanding improvement on the system performance. On the same time, the horizontal speed of AUG under different buoyancy is analyzed. All above make a foundation for the design of AUG.

autonomous underwater glider, PID controller, hydrodynamics

2016年2月10日,

2016年3月29日

鐘曉鋒，男，工程師，研究方向：魚雷總體及控制，信號處理。

TG156

10.3969/j.issn.1672-9730.2016.08.043