鉛期貨套期保值比率的估計

【摘要】本文結合Copula函數和協整理論兩方面優勢，同時考慮到金融市場收益率序列可能存在的偏態和尖峰厚尾特征，構造了一個基于時變的正太Copula函數的GJR-Skew-t分布的套期保值比率估計模型。并且對比分析了傳統的CCC-GARCH模型和DCC-GARCH模型的套期保值效果，實證研究表明：時變的正太Copula-GJR模型的套期保值比率最優并且套期保值效果較好，使用該模型可以提高收益率的均值，同時減少風險。

【關鍵詞】套期保值比率 CCC-GARCH模型 DCC-GARCH模型 Copula-GJR模型 GJR-Skew-t分布

一、引言

隨著經濟全球化和貿易自由化進程的推進以及全球資本流動的增加，全球大宗商品價格、股票指數、國際匯率均呈現出頻繁且劇烈的波動。在這一背景下，越來越多的實體經濟和金融部門面臨著資產價格風險管理的需要，規避現貨價格波動風險最為簡單有效的方法之一就是進行套期保值操作。目前，國外已有大量計量分析模型被用于金融期貨套期保值的實證研究中，但是我國現階段期貨市場并不十分完善，加上經濟環境的不確定性，國外相關實證研究結論未必完全適合我國期貨市場。另外，從方法上，國外不少文獻均采用GARCH模型等方法，但是傳統套期保值模型的缺陷在于忽視了現貨與期貨之間的動態相關性，當期貨與現貨收益率在某些階段表現出不同的波動時，往往導致套期保值比率失真。本文在傳統套期保值模型的基礎上，采用基于動態正太copula函數的GJR-Skew-t模型，可以很好的捕捉到相關變量間的非線性、非對稱相關關系以及尖峰厚尾等特征，這有助于豐富和完善我國期貨市場的套期保值模型實證研究。

二、文獻回顧

Johnson（1960）[1]和Ederington（1979）[2]等較早地利用投資組合理論來解釋套期保值，并分別將最小方差套期保值比率應用到金融期貨市場，進一步提出了金融期貨市場套期保值績效衡量指標。但隨著計量時間序列模型和金融數學的發展，很多學者開始懷疑使用普通最小二乘法（OLS）計算的最小風險套期保值比率。這是因為經過普通最小二乘法回歸之后的殘差項之間存在著相關性問題。為了消除殘差項的序列相關性對套期保值比率的影響，相關學者又引入了誤差修正模型來計算最小風險套期保值比率。Ghosh（1993）[3]充分考慮現貨價格與期貨價格間存在的協整關系，將協整理論引入套期保值比率研究中，構建了一個誤差修正模型（Error Correction Model，ECM），實證結果表明，忽視時間序列間的協整關系將導致計算出的套期保值比率小于最優值。

隨著自回歸條件異方差模型（ARCH）的發展和應用，越來越多的學者開始從動態的角度去研究最優套期保值比率，提出了基于條件異方差的動態套期保值比率計算方法。Baillie and Myers（1991）[4]在傳統方法的基本上了，考慮到時間序列的條件異方差性，利用GARCH模型對小麥期貨的最優套期保值比率進行估計，并且解釋變量和被解釋變的方差是信息集為條件的，因而最優套期保值比率會隨著信息集的變化而變化，而信息集是隨著時間的改變而改變的，所以最優套期保值比率為一動態變量而非靜態的。Kroner和Sultan（1993）[5]考慮協整關系和條件異方差性相結合，提出ECM-GARCH模型，并且利用該模型估計了英鎊、日元和加元等貨幣期貨的最有套期保值比率，結果發現動態套期保值更能減少組合風險。Alizadeh和Nomikos（2007）[6]，馬超群等（2008）[7]等學者基于GARCH類的模型進行實證研究發現，無論是對于商品期貨還是股指期貨，基于GARCH模型的動態套期保值模型估計比率要優于任何常相關系數套期保值模型估計的比率，且套期保值效果要更好。

上面的文獻中構造的二元GARCH模型來估計動態套期保值比大多是在假設期貨和現貨收益率的聯合分布服從多元正太分布的情況下進行的，但是忽視了可能存在的非正太雙變量相依結構的影響，事實上這一假設與金融時間序列普遍存在的尖峰后尾以及偏態特征也不相符合。近年來隨著Copula函數理論在金融研究領域的應用越來越廣泛，其在構造聯合分布和估計相關機構方面的優勢凸顯，因為它放寬了正態分布的假設，并且可以通過不同的相關結構將不同的邊際分布結合起來構造多維聯合分布，從而可以更好地描述金融序列的分布特征。馬超群等（2011）[8]對比分析了CCC-GARCH模型、ECM-GARCH模型以及copula-GARCH三種模型在外匯期貨套期保值中的效果，結果發現基于copula-GARCH模型的套期保值效果最好。張高勛等（2011）[9]通過將協整理論與copula函數理論結合起來，構造了一個copula- ECM-GARCH模型，研究發現在該模型下套期保值資產組合的收益率不僅提高了而且相對風險還降低了90%。謝赤等（2013）[10]以黃金偉實證研究對象，建立M-Copula-GJR-VaR動態套期保值比率估計模型，并且通過對比分析與CCC-GARCH模型、DCC- GARCH模型、Clayton Copula-GJR模型和Gumbel Copula- GJR模型的套期保值效果，研究發現采用M-Copula-GJR-VaR模型估計的套期保值比率最優且套期保值效果最好。

綜上所述，盡管現有文獻通過構造copula-GARCH模型能夠有效地降低套期保值組合風險，但是這些研究忽視了期貨與現貨收益率之間相關結構的非對稱特征。考慮到金融市場中不僅存在著不動的非對稱效應，而且考慮到金融資產時間序列分布呈現一定的偏態和尖峰厚尾特征，本文構造了一個二元條件下基于copula函數的GJR-Skew-t分布模型，該模型不僅能夠降低由于樣本數據中存在的尖峰厚尾以及非對稱分布特征導致的估計結構中可能出現的模型設定誤差，而且還可以刻畫現貨和期貨收益率序列之間相關結構的非對稱性和動態性特征，從而提高套期保值效果。最后將copula-GJR-Skew-t模型與CCC-GARCH模型以及DCC- GARCH模型進行比較分析。

三、實證分析

（一）數據來源及處理

本文以上海期貨交易所的鉛期貨和長江有色金屬市場鉛現貨為研究對象，收集了2011年5月4日至2012年4月17日的共259個鉛現貨和鉛期貨價格數據。數據處理上我們選取了在任何時點的后一個月進入交割月的期貨合約的中間價格作為分析對象，所以對期貨數據只取到期貨合約到期前倒數第二個月的數據，并使現貨時間與期貨時間對應，以上數據均來自國泰安數據庫。由于金融市場價格序列一般都具有非平穩的時間序列特征，所以本文對收盤價進行數據處理，本文資產價格均采用對數價格形式，并且將現貨價格轉變成對數收益率序列rts，t=lnst-lnst-1，期貨價格轉變成對數收益率序列rtf，t=lnft-lnft-1。數據處理軟件為matlab7.0，Eviews6.0和excel2007。

（二）模型參數估計結果

CCC-GARCH模型和DCC-GARCH模型的參數估計結果表明，在1%的顯著性水平下，GARCH項和ARCH項系數之和（即）均小于1，滿足模型平穩性的要求。對模型殘差項進行異方差檢驗后，發現異方差現象不明顯。以上結果表明上述兩種模型能夠較好的反映數據的波動性特征。

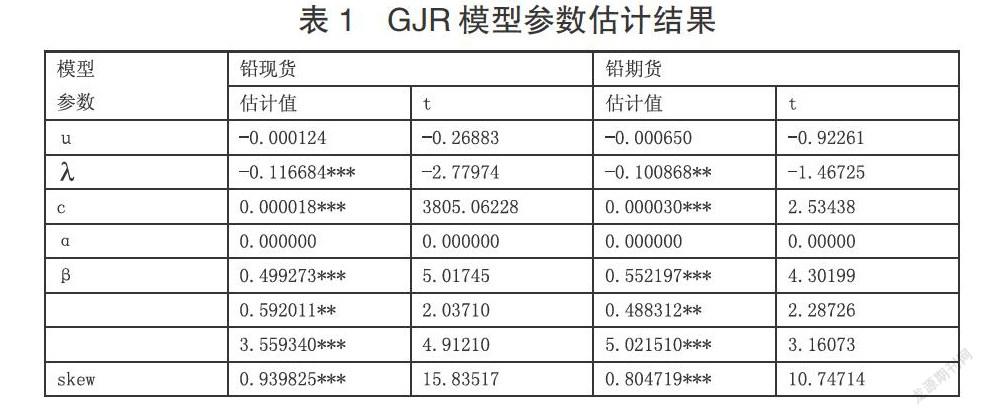
對基于時變的正太copula-GJR-skew-t模型進行估計得到的結果如表1所示。因為值都接近于1，說明兩個市場具有較強的波動持續性。模型參數的值都大于0，且從它們的t統計量來看都是顯著的，這說明利空消息造成的沖擊較利好消息引起的沖擊對市場影響更大，即兩個市場都存在非對稱效應，因此，采用GJR模型來估計各收益率序列的條件方差是較為合理的。鉛現貨收益率和鉛期貨收益率的GARCH項β均在5%的顯著性水平顯著，說明鉛現貨和鉛期貨收益率存在明顯的波動聚集特征。鉛現貨和鉛期貨收益率的ARCH和GARCH項之和（即α+β之和）小于1，滿足限制條件。從自由度v看，現貨和期貨收益率的自由度都大于3，且在5%的顯著性水平下顯著，而兩者自由度并不相同，這又從側面證明了傳統的多元分布理論并不合適。因此引入Copula函數來描述現貨收益率和期貨收益率的相關結構是合理的。

表1 GJR模型參數估計結果

四、結論

本文結合Kroner和Sultan（1993）ECM-GARCH模型和copula函數兩方面的優勢，同時結合金融時間序列的可能存在的尖峰厚尾以及非對稱分布特征，構造了一個時變的正太Copula-GJR模型，從而可以比較全面的刻畫現貨和期貨收益率序列之間相關結構的非對稱性和動態性特征。

參考文獻

[1]Johnson L L.The theory of hedging and speculation in commodity futures[J].The Review of Economic Studies，1960，27（3）；139-151.

[2]Ederington L H.Portfolio selection[J].The Journal of Finance，1979，34（1）：157-170.

[3]Ghosh A.Hedging with stock index futures： Estimation and furcating with error correction model[J].The Journal of Futures Markets，1993，13（7）：743-752.

[4]Baillie R T，Myers R J.Bivariate GARCH estimation of the optimal commodity futures hedge[J]. Journal of applied econometrics，1991，6109-6124.

[5]Korner K F，Sultan J.Time-varying distributions and dynamic hedging with foreign currency futures[J]. Journal of Financial and Quantitative Analysis，1993，（28）：535-551.

[6]Amir A，Nikos N.A Markov Regime Switching Approach for Hedging Stock Indics[J].Journal of Futures Markets，2004，24：649-674.

[7]馬超群，劉鈺，姚錚等。股指期貨最小風險套期保值比率計算方法及實證研究[J].系統工程，2008，26：80-84.

[8]馬超群，王寶兵.基于Copula-GARCH模型的外匯期貨最優套期保值比率研究[J].統計與決策，2011（12）：124-128.

[9]張高勛，田益祥，李秋敏.基于Copula-ECM-GARCH模型的動態最優套期保值比率估計及比較[J].系統工程，2011，29（8）：56-64.

[10]謝赤，屈敏，王綱金.基于M-Copula-GJR-VaR模型的黃金市場最優套期保值比率研究[J].管理科學，2013，26（2）：90-99.

作者簡介：劉希曦（1991-），女，漢族，就讀于武漢大學經濟與管理學院，碩士研究生，金融工程專業。