基于均勻設(shè)計(jì)理論的非矩形試驗(yàn)區(qū)域恒加壽命試驗(yàn)優(yōu)化設(shè)計(jì)方法
陳文華 朱志鵬 高 亮 潘 駿 孔祥澤
1.浙江理工大學(xué)浙江省機(jī)電產(chǎn)品可靠性技術(shù)研究重點(diǎn)實(shí)驗(yàn)室,杭州,3100182.四川農(nóng)業(yè)大學(xué),雅安,625014
?
基于均勻設(shè)計(jì)理論的非矩形試驗(yàn)區(qū)域恒加壽命試驗(yàn)優(yōu)化設(shè)計(jì)方法
陳文華1朱志鵬1高 亮2潘 駿1孔祥澤1
1.浙江理工大學(xué)浙江省機(jī)電產(chǎn)品可靠性技術(shù)研究重點(diǎn)實(shí)驗(yàn)室,杭州,3100182.四川農(nóng)業(yè)大學(xué),雅安,625014
針對(duì)基于Escobar和Meeker設(shè)計(jì)思想的非矩形試驗(yàn)區(qū)域最優(yōu)試驗(yàn)方案設(shè)計(jì),當(dāng)邊界較為復(fù)雜時(shí)失效概率最大點(diǎn)難以求得的問(wèn)題,以正常應(yīng)力下壽命估計(jì)值的漸近方差最小為目標(biāo),在非矩形區(qū)域內(nèi)選擇兩個(gè)應(yīng)力水平點(diǎn)分別作為最高和最低應(yīng)力水平點(diǎn),以最高、最低應(yīng)力水平以及各試驗(yàn)樣本分配比例為設(shè)計(jì)變量,提出了一種基于均勻設(shè)計(jì)理論的非矩形試驗(yàn)區(qū)域恒加壽命試驗(yàn)方案優(yōu)化設(shè)計(jì)方法。模擬計(jì)算結(jié)果表明,與基于Escobar和Meeker設(shè)計(jì)思想的最優(yōu)試驗(yàn)方案相比較,所提出的設(shè)計(jì)方法具有相同的估計(jì)精度,為非矩形試驗(yàn)區(qū)域加速壽命試驗(yàn)方案設(shè)計(jì)提供了一種簡(jiǎn)便的方法。
均勻設(shè)計(jì);非矩形試驗(yàn)區(qū)域;恒加壽命試驗(yàn);優(yōu)化設(shè)計(jì)
0 引言
恒定應(yīng)力加速壽命試驗(yàn)是目前工程上快速評(píng)估產(chǎn)品壽命的常用方法。設(shè)計(jì)最優(yōu)恒加壽命試驗(yàn)方案,是快速、經(jīng)濟(jì)地評(píng)估產(chǎn)品壽命的重要環(huán)節(jié)。對(duì)于兩應(yīng)力的恒加試驗(yàn),目前多在兩試驗(yàn)應(yīng)力構(gòu)成的矩形區(qū)域[1-7]內(nèi)進(jìn)行試驗(yàn)方案優(yōu)化設(shè)計(jì)。然而在工程實(shí)際中,由于試驗(yàn)設(shè)備的限制等原因,有時(shí)一個(gè)應(yīng)力的取值會(huì)限制另一個(gè)應(yīng)力,使得兩個(gè)應(yīng)力不能同時(shí)達(dá)到最大值,試驗(yàn)區(qū)域成為非矩形[8]。對(duì)于非矩形試驗(yàn)區(qū)域上的兩應(yīng)力加速壽命試驗(yàn),如果按照傳統(tǒng)矩形區(qū)域上的方法設(shè)計(jì)最優(yōu)試驗(yàn)方案,會(huì)出現(xiàn)應(yīng)力水平組合點(diǎn)位于試驗(yàn)區(qū)域之外的情況,不能保證獲得可行的方案。因此,有必要研究適用于非矩形試驗(yàn)區(qū)域的綜合應(yīng)力加速壽命試驗(yàn)方案的設(shè)計(jì)方法。
對(duì)于非矩形試驗(yàn)區(qū)域的最優(yōu)恒加試驗(yàn)方案設(shè)計(jì),Escobar等[9]針對(duì)矩形區(qū)域右上角被線性失效物理方程等值線截去而形成的非矩形區(qū)域,給出了優(yōu)化設(shè)計(jì)方法。Chen等[8]將Escobar等的設(shè)計(jì)思想推廣至具有任意邊界形狀的非矩形試驗(yàn)區(qū)域,建立了相應(yīng)的最優(yōu)試驗(yàn)方案設(shè)計(jì)方法。文獻(xiàn)[8-9]中的方法在設(shè)計(jì)過(guò)程中需要求出邊界上失效概率最大的點(diǎn),當(dāng)非矩形的邊界較為復(fù)雜,難以直接求出失效概率最大的點(diǎn)時(shí),會(huì)增加試驗(yàn)方案設(shè)計(jì)的難度。因此,一種不需要求失效概率最大點(diǎn)且估計(jì)精度也較高的試驗(yàn)方案設(shè)計(jì)方法,不失為一種簡(jiǎn)便可行的辦法。均勻設(shè)計(jì)[10]是一種考慮試驗(yàn)點(diǎn)在試驗(yàn)區(qū)域內(nèi)均勻散布的試驗(yàn)設(shè)計(jì)方法,與其他設(shè)計(jì)方法相比,壽命估計(jì)精度較高。
本文針對(duì)機(jī)電產(chǎn)品普遍適用的線性-極值模型,以正常應(yīng)力下壽命分布P階分位數(shù)極大似然估計(jì)值的漸近方差最小為設(shè)計(jì)準(zhǔn)則,在非矩形區(qū)域內(nèi)選擇兩個(gè)應(yīng)力水平分別作為最高和最低應(yīng)力水平點(diǎn),以最高、最低應(yīng)力水平點(diǎn)以及各應(yīng)力水平點(diǎn)試樣分配比例作為優(yōu)化設(shè)計(jì)變量,限制各試驗(yàn)應(yīng)力組合點(diǎn)在最高應(yīng)力水平點(diǎn)和最低應(yīng)力水平點(diǎn)為對(duì)角的矩形區(qū)域內(nèi)等間隔均勻分布,通過(guò)對(duì)試驗(yàn)方案進(jìn)行優(yōu)化設(shè)計(jì),以達(dá)到文獻(xiàn)[9]的試驗(yàn)效果,并簡(jiǎn)化非矩形區(qū)域恒加壽命試驗(yàn)方案優(yōu)化設(shè)計(jì)方法。
1 模型假設(shè)
(1)在試驗(yàn)區(qū)域上的所有應(yīng)力水平組合(試驗(yàn)點(diǎn)),產(chǎn)品的對(duì)數(shù)壽命θ服從極值分布,其概率分布函數(shù)為
F(θ)=1-exp{-exp[(θ-μ)/σ]}
式中,μ為位置參數(shù);σ為尺度參數(shù)。
(2)在試驗(yàn)區(qū)域中,位置參數(shù)μ與標(biāo)準(zhǔn)化處理(具體標(biāo)準(zhǔn)化的方法參見(jiàn)文獻(xiàn)[8-9],下同)后的試驗(yàn)應(yīng)力u、v滿足:
μ(u,v)=γ0+γ1u+γ2v
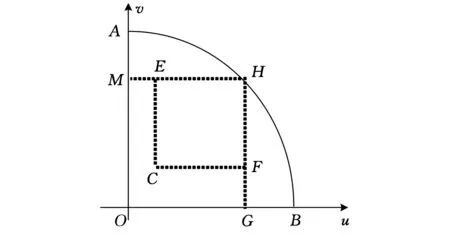
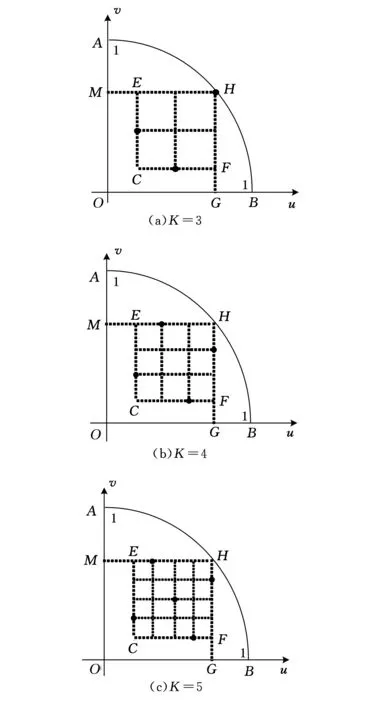
其中,0 (3)在試驗(yàn)區(qū)域中,尺度參數(shù)σ與應(yīng)力點(diǎn)坐標(biāo)無(wú)關(guān),為常數(shù)。 (4)各試驗(yàn)樣本的壽命相互獨(dú)立。 (5)采用定時(shí)截尾恒加壽命試驗(yàn),各個(gè)應(yīng)力水平組合上的截尾時(shí)間相等,均為τ。 由文獻(xiàn)[2-4]可知,大多數(shù)機(jī)電產(chǎn)品的統(tǒng)計(jì)模型都可以轉(zhuǎn)化為上述線性-極值模型。 首先,將一般非矩形試驗(yàn)區(qū)域標(biāo)準(zhǔn)化[8-9],如圖1所示,A(0,1)、B(1,0),O(0,0)為正常應(yīng)力水平點(diǎn)。SAB為非矩形試驗(yàn)區(qū)域邊界曲線,設(shè)SAB的曲線方程為v=f(u),0 圖1 標(biāo)準(zhǔn)化后的非矩形區(qū)域 矩形試驗(yàn)區(qū)域上的方案優(yōu)化,按失效機(jī)理不變的原則選定最高應(yīng)力水平點(diǎn)后,只需優(yōu)化最低應(yīng)力水平點(diǎn)即可。但在非矩形試驗(yàn)區(qū)域中,最高應(yīng)力水平點(diǎn)的選定,除了要滿足失效機(jī)理不變的原則外,還需按試驗(yàn)精度最高的原則,在非矩形試驗(yàn)區(qū)域內(nèi)通過(guò)優(yōu)化選定。通過(guò)分析可以證明[1],試驗(yàn)的最高應(yīng)力水平越高,產(chǎn)品在正常工作應(yīng)力水平下壽命分布P階分位數(shù)極大似然估計(jì)值的標(biāo)準(zhǔn)離差越小。過(guò)試驗(yàn)區(qū)域OAB內(nèi)某點(diǎn)作失效物理方程的等值線l=μ*=γ0+γ1u+γ2v可以證明[8],當(dāng)該點(diǎn)在曲線SAB上時(shí),其失效概率比在區(qū)域OAB內(nèi)要大(過(guò)曲線SAB上的點(diǎn)μ*在v軸截距較大),因此,在邊界SAB上優(yōu)選最高應(yīng)力水平點(diǎn),可保證壽命估計(jì)值的方差較小。 試驗(yàn)方案優(yōu)化時(shí),在邊界曲線SAB上任取一點(diǎn)H(uH,f(uH))作為最高應(yīng)力水平點(diǎn),然后,在矩形區(qū)域OMHG內(nèi)就給定的應(yīng)力水平數(shù)K按均勻組合的方式,以正常應(yīng)力水平下壽命估計(jì)值的漸近方差最小為目標(biāo)對(duì)最低應(yīng)力水平點(diǎn)C(uC,vC)進(jìn)行優(yōu)化,具體方法如下。 給定應(yīng)力水平K,其他應(yīng)力水平可由最高應(yīng)力水平點(diǎn)H和最低應(yīng)力水平點(diǎn)C按等間隔應(yīng)力水平分配原則來(lái)表示: i=1,2,…,K 在估計(jì)精度基本保持不變的前提下,為減少試驗(yàn)次數(shù),采用均勻設(shè)計(jì)理論對(duì)應(yīng)力水平進(jìn)行組合。按均勻設(shè)計(jì)理論,同一個(gè)應(yīng)力水平,按照均勻設(shè)計(jì)理論會(huì)有多種不同的應(yīng)力點(diǎn)組合方式,但其方差因子的值不同,方差因子值最小的應(yīng)力點(diǎn)組合方式為最佳組合方式。當(dāng)應(yīng)力水平K分別為3、4、5時(shí),應(yīng)力點(diǎn)的最佳組合方式如圖2所示(圖中實(shí)心圓點(diǎn)代表應(yīng)力點(diǎn)的分布位置)。 圖2 基于均勻設(shè)計(jì)理論最佳應(yīng)力點(diǎn)組合方式 在取定H點(diǎn)所形成的矩形區(qū)域OMHG內(nèi)以方差因子最小為目標(biāo)優(yōu)化出C點(diǎn)后,可以得到該最高應(yīng)力水平點(diǎn)下的優(yōu)化試驗(yàn)方案坐標(biāo)(ui,vi),i=1,2,…,K,其分布如圖2中實(shí)心圓點(diǎn)所示。 取遍曲線SAB上每一點(diǎn)作為最高應(yīng)力水平H,比較每一個(gè)H點(diǎn)下最優(yōu)試驗(yàn)方案方差因子值VK,VK最小時(shí)的H點(diǎn)即為最優(yōu)點(diǎn),相應(yīng)的最優(yōu)試驗(yàn)方案為最后優(yōu)選的試驗(yàn)方案。 當(dāng)邊界為凹域時(shí),按照上述方法設(shè)計(jì)的試驗(yàn)方案,試驗(yàn)點(diǎn)有可能在試驗(yàn)區(qū)域外,故以上方法只針對(duì)邊界為凸域的非矩形試驗(yàn)區(qū)域。 試驗(yàn)區(qū)域經(jīng)過(guò)標(biāo)準(zhǔn)化處理后,正常工作應(yīng)力水平點(diǎn)為(0,0),約束最高應(yīng)力水平點(diǎn)在邊界上取值,即vH=f(uH),相應(yīng)的優(yōu)化模型可以表示為[3] (σ2/N)VK s.t.0=u0≤ui≤uH≤1 0=v0≤vi≤vH≤1 vH=f(uH) 經(jīng)過(guò)標(biāo)準(zhǔn)化后的fisher信息矩陣如下[8]: A(ζi)=1-exp(-expζi) ζi=(lnτ-γ0-γ1ui-γ2vi)/σ 因?yàn)棣?/N為常數(shù),故優(yōu)化時(shí)可將目標(biāo)函數(shù)簡(jiǎn)化為求VK的最小值。 如圖3所示,設(shè)試驗(yàn)區(qū)域OBMQRA的邊界SAB由拋物線BM、線段MQ、線段QR和圓弧RA組成。點(diǎn)M、Q、R的坐標(biāo)分別為(0.7946,0.9)、(0.8748,0.4845)和(0.8748,0.6),各分段的方程分別為 圖3 算例示意圖 分別考慮在應(yīng)力水平K=3、4、5時(shí)的最優(yōu)試驗(yàn)方案設(shè)計(jì)。由于算例中的邊界曲線比較復(fù)雜,是由分段函數(shù)構(gòu)成的邊界曲線,故試驗(yàn)方案優(yōu)化時(shí)需在曲線段BM、MQ、QR、RA上分別找出最優(yōu)試驗(yàn)方案,再通過(guò)比較找出最后優(yōu)選的試驗(yàn)方案。 (1)按第3節(jié)中優(yōu)化設(shè)計(jì)方法分別求出K=3、4、5時(shí)的基于均勻設(shè)計(jì)理論的恒加壽命試驗(yàn)方案(簡(jiǎn)稱U-3、U-4、U-5)。其各應(yīng)力組合點(diǎn)分布如圖4中實(shí)心圓點(diǎn)所示,各試驗(yàn)方案對(duì)應(yīng)的方差因子分別為72.0746、85.7891、85.9401。 圖4 基于均勻設(shè)計(jì)理論的優(yōu)化試驗(yàn)方案應(yīng)力點(diǎn)分布 (2)按文獻(xiàn)[9]中方法分別求出K=3、4、5時(shí)基于Escobar和Meeker設(shè)計(jì)思想分裂得到的試驗(yàn)方案(簡(jiǎn)稱EM-3、EM-4-1、EM-4-2、EM-5,其中EM-4-1和EM-4-2指K=4時(shí)的兩種應(yīng)力組合方式),其方差因子分別為71.0184、87.2230、87.2230、87.2230。 (3)比較兩種不同設(shè)計(jì)方法所得最優(yōu)試驗(yàn)方案的方差因子可得,基于均勻設(shè)計(jì)理論的優(yōu)化設(shè)計(jì)方案的方差因子與按文獻(xiàn)[9]中方法求出最優(yōu)試驗(yàn)方案的方差因子相差不大,甚至在K=4,5時(shí)方差因子更小,因此,基于均勻設(shè)計(jì)的試驗(yàn)方案同樣具有較好的估計(jì)精度。 綜上,針對(duì)算例求得的基于均勻設(shè)計(jì)理論的優(yōu)化設(shè)計(jì)方案見(jiàn)表1,試驗(yàn)點(diǎn)的位置分布如圖4中實(shí)心圓點(diǎn)所示。 本文根據(jù)均勻設(shè)計(jì)理論,以在正常應(yīng)力水平時(shí)P階分位數(shù)極大似然估計(jì)值的漸近方差最小為準(zhǔn)則,在非矩形區(qū)域內(nèi)選擇兩個(gè)應(yīng)力水平點(diǎn)分別作為最高和最低應(yīng)力水平點(diǎn),以最高、最低應(yīng)力水平點(diǎn)以及各應(yīng)力水平點(diǎn)試樣分配比例作為優(yōu)化設(shè)計(jì)變量,限制各試驗(yàn)應(yīng)力組合點(diǎn)在最高應(yīng)力水平點(diǎn)和最低應(yīng)力水平點(diǎn)為對(duì)角的矩形區(qū)域內(nèi)等間隔均勻分布,建立了基于均勻設(shè)計(jì)理論的非矩形區(qū)域恒加試驗(yàn)方案優(yōu)化設(shè)計(jì)方法。最后,通過(guò)算例和基于Escobar和Meeker設(shè)計(jì)思想的最優(yōu)試驗(yàn)方案比較,結(jié)果表明本文的試驗(yàn)方案具有較好的壽命估計(jì)精度,是可行的試驗(yàn)方案,為非矩形試驗(yàn)區(qū)域上的最優(yōu)試驗(yàn)方案設(shè)計(jì)提供了一種新的思路和方法。 表1 應(yīng)力水平數(shù)K=3,4,5時(shí)算例優(yōu)化設(shè)計(jì)結(jié)果 [1]NelsonW.AcceleratedTestingStatisticalModels,TestPlansandDataAnalysis[M].NewYork:AWileyinte-sciencePublication,JohnWiley&Sons,1990. [2]陳文華,馮紅藝,錢(qián)萍,等.綜合應(yīng)力加速壽命試驗(yàn)方案優(yōu)化設(shè)計(jì)理論與方法[J].機(jī)械工程學(xué)報(bào), 2006,42(12):101-105. ChenWenhua,Fenghongyi,QianPing,etal.OptimalDesignofMultipleStressesAcceleratedLifeTestPlan[J].ChineseJournalofMechanicalEngineering,2006,42(12):101-105. [3]GaoLiang,ChenWenhua,LiuJuan,etal.DesignCriteriaforPlanningMultipleStressAcceleratedLifeTest[C]//TheProceedingson2011 9thInternationalConferenceonReliabilityMaintainability&Safety.Guiyang,2011:1141-1146. [4]陳文華,錢(qián)萍,馬子魁,等.基于定時(shí)測(cè)試的綜合應(yīng)力加速壽命試驗(yàn)方案優(yōu)化設(shè)計(jì)[J].儀器儀表學(xué)報(bào),2009,30(12):2345-2550. ChenWenhua,QianPing,MaZikui,etal.OptimalDesignofMultipleStressesAcceleratedLifeTestPlanundertypeICensoring[J].ChineseJournalofScientificInstrument,2009,30(12):2345-2550. [5]NelsonWB.AcceleratedTesting:StatisticalModels,TestPlans,DataAnalyses[M].NewYork:Wiley,1990. [6]ParkJW,YumBJ.OptimalDesignofAcceleratedLifeTestingwithTwoStress[J].NavalResearchLogistics,1996,43(6):863-884. [7]GuoHuairui,PanRong.D-optimalReliabilityTestDesignforTwo-stressAcceleratedLifeTests[C]//Proceedingsofthe2007IEEEIEEM.Singapore,2007:1236-1240. [8]ChenWenhua,GaoLiang,etal.OptimalDesignofMultipleStressAcceleratedLifeTestPlanontheNon-rectangleTestRegion[J].ChineseJournalofMechanicalEngineering,2012,25(6):1231-1237. [9]EscobarLA,MeekerWQ.PlanningAcceleratedLifeTestswithTwoorMoreExperimentalFactors[J].Technometrics,1995,37(4):411-427. [10]方開(kāi)泰,馬長(zhǎng)興.正交與均勻試驗(yàn)設(shè)計(jì)[M].北京: 科學(xué)出版社,2001. [11]GaoLiang,ChenWenhua,QianPing,etal.OptimalDesignofMultipleStressesAcceleratedLifeTestPlanBasedonTransformingtheMultipleStressestoSingleStress[J].ChineseJournalofMechanicalEngineering,2014,28(6):1125-1132. (編輯陳勇) Optimum Design of Accelerated Life Test Plan on non-rectangle Test Region Based on Uniform Design Theory Chen Wenhua1Zhu Zhipeng1Gao Liang2Pan Jun1Kong Xiangze1 1.Zhejiang Province’s Key Laboratory of Reliability Technology for Mechanical and Electrical Product, Zhejiang Sci-Tech University, Hangzhou,310018 2. Sichuan Agricultural University,Ya’an,Sichuan,625014 Aiming at the problems of hardly finding out the points of the maximum probability of failure on the complicated boundary curves when designed the optimal multiple stress accelerated life test plan on the non-rectangle test region based on Escobar-Meeker method, minimum variance of product life estimated value at normal working stresses was taken as design object for constant stress accelerated life test method. After selecting two stress level points as the highest level point and the lowest level point on the non-rectangle test region , the highest stress level , the lowest stress level of each accelerated factor and allocation proportion of test samples were adopted as design variables; the optimum design method of multiple stress accelerated life test on the non-rectangle test region was built based on uniform design theory. The computer simulation results show that the optimized test plan has the same estimation precision of test data compared to the optimized test plan based on the Escobar-Meeker method. The research fruits provide a simple method for the test plan design of multiple stress accelerated life test on the non-rectangle test region. uniform design; non-rectangle test region; constant accelerated life test; optimum design 2015-10-08 國(guó)家自然科學(xué)基金資助項(xiàng)目(51275480);浙江省重點(diǎn)科技創(chuàng)新團(tuán)隊(duì)計(jì)劃資助項(xiàng)目(2010R50005) TB114.3;V442 10.3969/j.issn.1004-132X.2016.15.014 陳文華,男,1963年生。浙江理工大學(xué)機(jī)械與自動(dòng)控制學(xué)院教授、博士研究生導(dǎo)師。主要研究方向?yàn)榭煽啃栽O(shè)計(jì)、試驗(yàn)與統(tǒng)計(jì)分析。朱志鵬(通信作者) ,男,1990年生。浙江理工大學(xué)機(jī)械與自動(dòng)控制學(xué)院碩士研究生。高亮,男,1981年生。四川農(nóng)業(yè)大學(xué)信息與工程技術(shù)學(xué)院講師。潘駿,男,1974年生。浙江理工大學(xué)機(jī)械與自動(dòng)控制學(xué)院教授。孔祥澤,男,1989年生。浙江理工大學(xué)機(jī)械與自動(dòng)控制學(xué)院碩士研究生。2 試驗(yàn)方案優(yōu)化設(shè)計(jì)思路

3 試驗(yàn)方案優(yōu)化設(shè)計(jì)建模

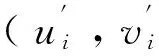
4 算例


5 結(jié)語(yǔ)