一類高維動力學系統的混沌預測同步實現方法研究

孫　濤 ， 秦衛陽

(西北工業大學 振動工程研究所，西安　710129)

?

一類高維動力學系統的混沌預測同步實現方法研究

孫濤1， 秦衛陽2

(西北工業大學 振動工程研究所，西安710129)

對于一類含有時間項的高維非線性動力學系統，提出了實現混沌預測同步的控制方法。在混沌同步的基礎上，建立了派生系統及差別方程，從理論上證明了提出的方法能夠實現對于原非線性系統的預測同步。對于耦合項進行了簡化，為了實現長時間的預測，建立了多級同步系統來延長預測同步時間。對于Duffing系統，以及含反饋單擺系統在混沌狀態下進行了仿真計算，證明了提出的方法是正確的與有效的。

混沌；預測同步；動力學系統

自從20世紀90年代Pecora等[1]提出混沌同步后，由于其獨特的特性和廣泛的存在性，該研究目前正在深化與細化。如混沌的廣義同步[2]，各種網絡內、網絡之間的混沌同步[3]，近年來分數階混沌系統的同步研究也出現了很多成果[4-6]。Lin等[7-8]研究了帶有隨機參數的不確定混沌系統的控制問題與同步問題，提出了自組織-自適應模糊神經控制方法與同步方法。Voss[9]提出了混沌預測同步的概念，即通過耦合，一個系統的混沌響應與另一個系統τ時刻后的混沌響應同步，這樣相當于實現了對于混沌的預測，具有重要的意義，因此自提出以后引起了很多研究者的重視。Wei[10]利用混沌的預測同步來識別系統的未知參數。Yan[11]提出了廣義預測同步的概念。對于原混沌系統，可以實現派生系統的k倍加速演化，這種預測同步具有全局性。Pyragas[12]為了實現長時間的混沌預測，對于耦合矩陣進行了研究，提出了最佳的耦合方式。Pyragiene[13]提出了一種新的耦合方式，派生系統包含兩個方程，每個方程帶有周期開關的參數，可以實現比較長時間的混沌預測。在預測同步的應用方面，Mayo[14]利用預測同步， 預先從派生系統中得到FitzHugh-Nagumo系統中不規則脈沖的發生，提前采取控制措施抑制它。結果表明控制的效果很好。

目前,對于含有時間項的一類高維動力學系統，實現混沌的預測同步，困難還比較大。本文在混沌同步的基礎上，對于一般的動力學系統，提出實現混沌預測同步的新方法，對于這種方法，進行了相關的理論證明與仿真驗證計算。

1　理論分析

實際中，含有非線性恢復力的一類高維動力學系統可以用如下方程表示：

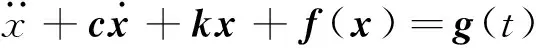
(1)

式中：x∈Rn×1為系統動力學響應向量，f(x)為系統內部非線性力，g(t)為外激勵。那么，采用線性耦合控制策略[1]，可以建立混沌同步派生系統：

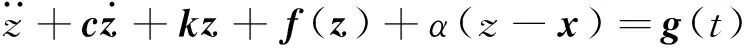
(2)

式中：α∈Rn×n為耦合系數矩陣。假設通過耦合可以實現系統混沌的同步，那么式(1)～式(2)得到的差別方程為：

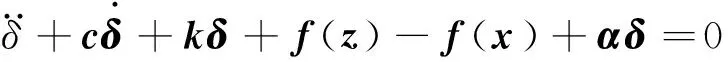
(3)

式中：δ=z-x。對函數項進行泰勒展開，保留一次項，有：

(4)

由于式(1)與式(2)同步，所以必然有：

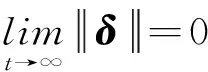
(5)

在實現了混沌的同步后，為了進一步實現混沌的預測同步，對于動力學系統(1)，建立如下的預測同步派生系統：

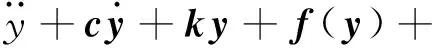
α(y-x(t+τ))=g(t+τ)

(6)

而對于方程(1)，在t+τ時刻方程可以寫為：

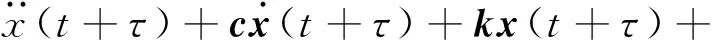
f(x(t+τ))=g(t+τ)

(7)

式(6)～式(7)有：

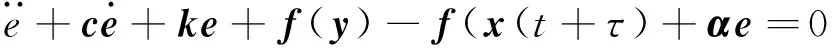
(8)

即：

(9)

可以看出，方程(9)與方程(4)具有相同的形式，則其平凡解具有相同的穩定性，即：

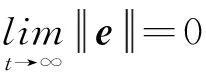
(10)

因此，通過方程(6)可以實現y(t)與x(t+τ)的同步。但是在方程(6)中，由于耦合項含有x(t+τ)項，實際中無法提前得到。為了解決這個問題，將x(t+τ)泰勒展開，取其前3項作為耦合項，即方程(6)變為：

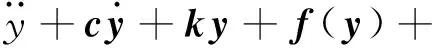
(11)

則同樣可以實現在t時刻附近的混沌預測同步。

為了進一步增加預測時間τ，可以采用建立多級耦合派生系統的方法，即：

g(t+τ1)

g(t+τ2)

?

g(t+τn)

(12)

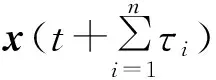
2　仿真計算

以二個混沌系統作為對象，進行了仿真計算，以驗證提出的同步方法。

(1) Duffing系統

考慮Duffing系統

(13)

在a=0.2，b=-1，c=1，f=0.28，ω=1.2 時，系統會出現混沌運動(圖1)。按照上述的方法，建立同步派生系統

fcosω(t+τ)

(14)

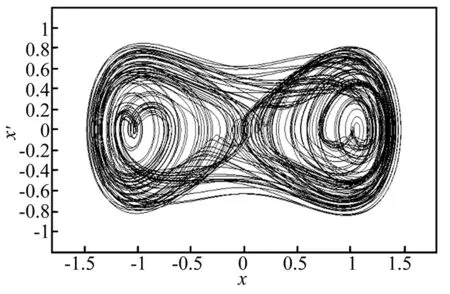
圖1　Duffing系統混沌相圖Fig.1 Chaotic phase diagram of Duffing system

為了增加預測時間，建立了5級派生系統，最終的預測時間∑τ=1.45 s，計算的結果如圖2、圖3所示。圖3顯示的是y-x(t+∑τ)隨時間的變化。可以看出，實現了派生系統對原混沌系統的預測同步。

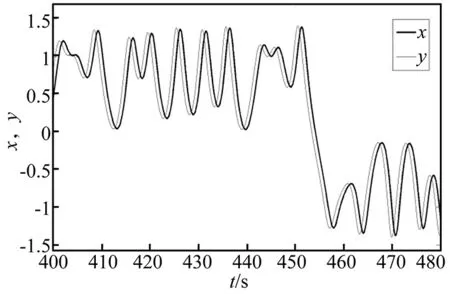
圖2　y與x的波形圖Fig.2 Waveform diagram(y,x)

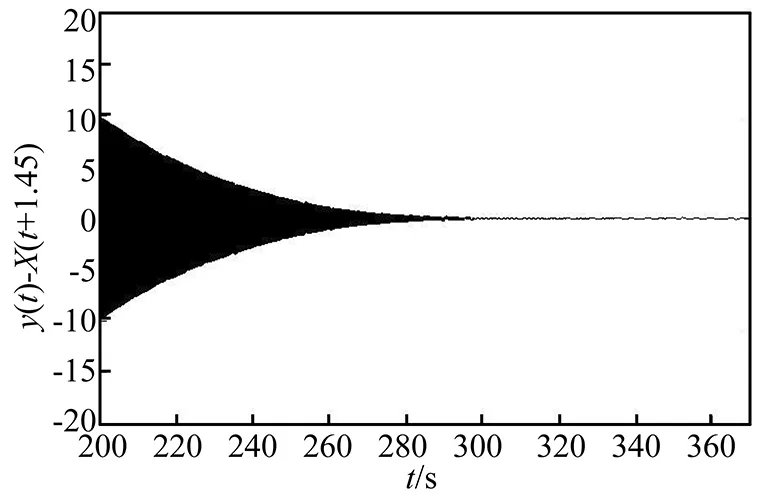
圖3　y(t)-x(t+1.45)隨時間的變化Fig.3 y(t)-x(t+1.45) change over time graph

(2) 帶反饋控制的混沌單擺系統

帶反饋控制的單擺方程為[8]：

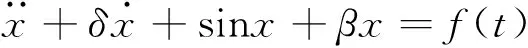
(15)

式中：

f(t)=(β-ω2)a1cosωt-δωa1sinωt+

sin(a1cosωt+a0)+βa0

ω為角速度，β為反饋增益，δ為阻尼比，a1是軌跡的幅值。當β=0.5，a0=-3，a1=0.3，δ=0.12，ω=0.75時，系統響應出現混沌(圖4)。按照上述分析，建立派生系統

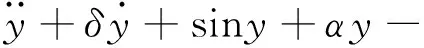
(16)

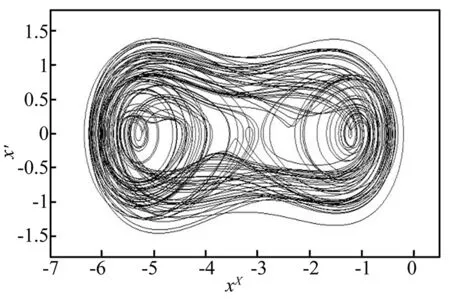
圖4　混沌擺的相圖Fig.4 The phase diagram of chaotic pendulum

同樣，為了增加預測時間，建立了5級耦合派生系統，最終的預測時間∑τ=1.9 s，計算的結果如圖5、圖6所示，由計算結果可以看出，此時實現了派生系統對于原系統的混沌預測同步。

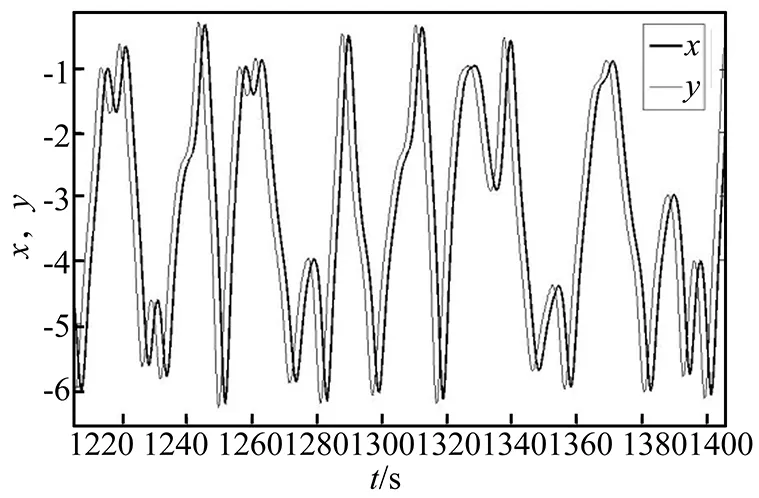
圖5　y與x的波形圖Fig.5 Waveform diagram(y,x)

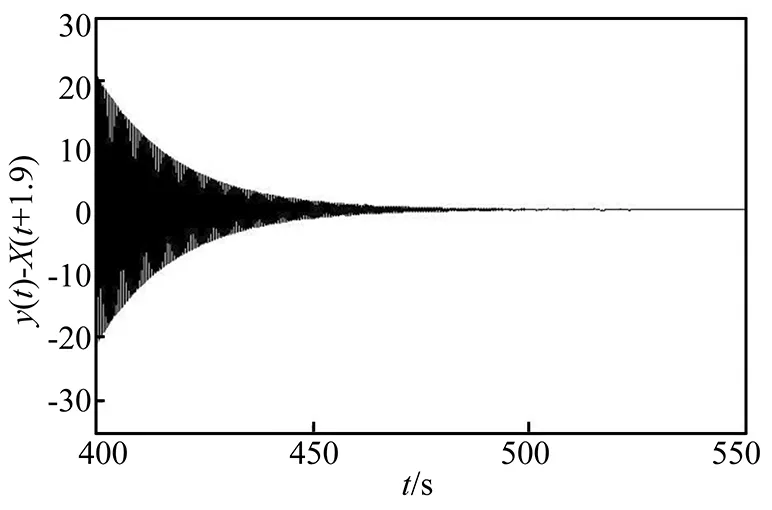
圖6　y(t)-x(t+1.9)隨時間的變化Fig.6 y(t)-x(t+1.9) change over time graph

3　結　論

對于非線性動力學系統，常常可以通過線性耦合實現混沌同步。本文在此基礎上，提出了一種實現高維非線性動力學系統混沌預測同步的方法，即實現一個系統的軌跡與原混沌系統τ秒以后的軌跡相同。通過理論分析，證明了提出的方法可以實現混沌的預測同步。然后，通過建立多級耦合系統，增加混沌預測同步的預測時間。以Duffing系統，以及含反饋控制的單擺系統作為對象，進行了仿真計算，證明了方法是正確的和有效的。

[1] Pecora L M，Carroll T L. Synchronization in chaotic systems[J]. Phys. Rev. Lett.，1990, 64(8): 821.

[2] 過榴曉，徐振源.關于非線性系統兩類廣義混沌同步存在性研究[J]. 物理學報，2008, 57(10): 6086.

GUO Liu-xiao, XU Zhen-yuan.The existence of two types of generalized synchronization of nonlinear systems[J]. Acta Phys. Sin. 2008, 57(10): 6086.

[3] 張檬，呂翎，呂娜, 等. 結構與參量不確定的網絡與網絡之間的混沌同步[J]. 物理學報，2012，61(22)：508.

ZHANG Meng, Lü Ling, Lü Na, et al. Chaos synchronization between complex networks with uncertain structures and unknown parameters[J]. Acta Phys. Sin,2012, 61(22): 508.

[4] Wang X, Song J. Synchronization of the fractional order hyperchaos Lorenz systems with activation feedback control[J]. Commun Nonlinear Sci Numer Simulat,2009,14:3351-3357.

[5] Wang X, Zhang X, Ma C. Modified projective synchronization of fractional-order chaotic systems via active sliding mode control[J]. Nonlinear Dyn, 2012, 69:511-517.

[6] 黃麗蓮， 齊雪. 基于自適應滑模控制的不同維分數階混沌系統的同步[J]. 物理學報，2013，62(8)：507.HUANG Li-lian, QI Xue. The synchronization of fractional order chaotic systems with diferente orders based on adaptive sliding mode control[J]. Acta Phys. Sin,2013, 62(8): 507.

[7] Lin D, Wang X, Nian F, et al. Dynamic fuzzy neural networks modeling and adaptive backstepping tracking control of uncertain chaotic systems[J]. Neurocomputing, 2010, 73: 2873-2881.

[8] Lin D, Wang X.Self-organizing adaptive fuzzy neural control for the synchronization of uncertain chaotic systems with random-varying parameters[J]. Neurocomputing, 2011, 74: 2241-2249.

[9] Voss H U. Anticipating chaotic synchronization[J].Phys. Rev. E. 2000,61:5115.

[10] Wei H, Li L. Estimating parameters by anticipating chaotic synchronization[J]. Chaos, 2010,20:023112.

[11] Yan H, Wei P, Xiao X. General anticipating response in coupled dynamical systems[J]. Chaos, 2009,19:023122.

[12] Pyragas K, Pyragienê T. Coupling design for a long-term anticipating synchronization of chaos[J]. Phys. Rev. E, 2008, 78:046217.

[13] Pyragiene T, Pyragas K. Anticipating synchronization in a chain of chaotic oscillators with switching parameters[J]. Physics Letters A, 2015, 379: 3084-3088.

[14] Mayo C, Mirasso C R, Tora R. Anticipated synchronization and the predict-prevent control method in the FitzHugh-Nagumo model system[J]. Phys. Rev. E, 2012, 85:056216.

Anticipated synchronization of chaos for a class of high dimensional dynamic systems

SUN Tao1, QIN Weiyang2

(Department of Engineering Mechanics, Northwestern Polytechnical University, Xi’an 710072, China)

For a class of high dimensional nonautonomous dynamic systems, the control method to realize anticipated synchronization of chaos was presented. Based on chaos synchronization, the derived system and difference equation for anticipated synchronization were built. It was proved that the control method can make the response of the derived system be identical with that of the original system within τ seconds theoretically. Furthermore, the coupling terms were simplified. To make the anticipation time longer, the multi-layer derived systems were built and they were coupled each other. A Duffing system and a pendulum with feedback were simulated to validate the correctness and effectiveness of the proposed method.

chaos; anticipated synchronization; dynamic system

國家自然科學基金(11172234)

2015-09-09修改稿收到日期：2016-01-24

孫濤 男，博士生，1983年3月生

秦衛陽 男，博士，教授，1967年4月生

O415.5

A

10.13465/j.cnki.jvs.2016.15.009