面向產品族優化設計的交互式模糊算法

張如川，杜　綱

(天津大學 管理與經濟學部，天津　300072)

?

面向產品族優化設計的交互式模糊算法

張如川，杜綱

(天津大學 管理與經濟學部，天津300072)

在大規模定制生產的背景下，產品族理論在近年成為學術界的熱點研究方向，并且在產品族設計階段就考慮到供應商、組裝商、零售商等主體的研究也逐漸增多。這種基于斯坦伯格博弈的產品族主從關聯優化模型往往具有復雜的數學性質，如下層有多個優化問題且有耦合變量、非線性、大量整數變量等，這會導致現有的求解算法往往無法處理。針對產品族主從關聯優化模型的數學性質，提出了一個基于交互式模糊算法的雙層規劃近似算法，并給出了應用算法解決實際的產品族配置-參數優化問題的實際算例。

產品族設計；雙層規劃；交互式模糊算法；斯坦伯格博弈

game

產品族(product family)作為產品的一種擴展表現形式，近年來已經成為理論界和企業界主流關注的重要主題。這不僅因為產品族及其設計是大規模定制的核心內容，而且因為產品族的架構策略作為獲取競爭優勢的重要手段已經成為企業競爭戰略的關鍵性構成要素。鑒于產品族的模型的多主體的特性，運用雙層規劃來描述企業的產品族策略成為近10年來的研究熱點。

自20世紀70年代末已有眾多學者對雙層以及多層優化理論及其解法進行了研究，在理論、算法設計等方面得到了許多成果。現有的解雙層規劃的算法大致有K-th最好法、KKT方法、下降類算法、罰函數法等。但由于雙層規劃問題是NP難題，所以這類方法往往只能解決解空間有特定性質的雙層規劃問題。因此，開發求解雙層規劃的近似算法具有重要的意義。

1996年Shih和Lai[1]提出了解多層優化問題的新算法框架，被稱作fuzzy approach，該算法考慮到將雙層優化的實質歸結為上下層目標的矛盾，通過引入目標函數和決策變量隸屬度函數確定上下層滿意度的閾值，將模型化為單層優化模型求解，在迭代中上層不斷調整滿意度閾值直到得到全局滿意模型。該算法不同于傳統的基于Stackelberg博弈的方法，在轉化問題的過程中沒有增加問題的復雜程度。之后的若干年不斷有學者在Shih和Lai的基礎上對該方法做出了相應研究。Shinha[2]在多層優化模型中運用此方法，Osman[3]將其推廣到非線性及多層多目標的模型中，L.Vicente等[4]將其運用到2次規劃中，Enam等[5]發展了該方法在整數非線性優化的運用。Sakawa等[6-12]在一系列的文獻中論證了Shih和Lai提出的方法[1]求解出非全局滿意解，由于上層決策者要指定目標函數的隸屬度函數和決策變量的隸屬度函數，這2個目標的不一致會導致求解結果不能達到全局滿意，甚至會導致可行域在迭代中不斷收縮直至成為空集。為了克服Shih和Lai所提方法的問題，Sakawa等提出了交互式模糊算法(interactive fuzzy approach)，運用迭代算子Δ實現上層決策者與下層決策者隸屬度的取舍。與此同時Sakawa等[6,11-12]還探索了在線性和分式優化中模糊因素對該算法的影響，并在其基礎上結合遺傳算法發展了交互式模糊算法在0-1整數優化及非凸問題中的應用[8-9]。

針對運用交互式模糊算法的思想來解決BLMFP問題，Wang,Wan在Sakawa[13]的基礎上提出了一種有共享變量的交互式模糊算法，但文章中給出的算法步驟并沒有體現出共享變量在決策機制中的作用，把共享變量和下層各自獨立決策的變量進行了相同的處理，在所構建算法中沒有體現共享變量在BLMFP問題中有別于獨立變量的性質。

本文通過總結以往學者的研究，結合模塊配置-參數設計型產品族模型的特點，提出一個求解BLMFP問題的交互式模糊算法，該算法具有以下特點：

1) 運用了有別于文獻[13]算法的隸屬度函數構建策略，以加快其收斂性；

2) 在算法設計中體現了下層多個規劃問題中的共享變量的特殊性質。

1　問題與模型的提出

1.1產品族主從關聯優化問題

產品族及其架構的設計本質上是主系統和子系統間相互關聯設計的問題。這種多主體的關系不僅體現在企業內部，也體現在企業同其供應商、組裝商、維修商上。在以往的文獻中，雖然對這些主體及其自身利益訴求對產品族及其架構設計的影響有大量研究，但大都是All in One的一攬子靜態決策，沒有體現主體之間相互博弈和相互權衡的思想。由于這些思想無法用傳統的單層規劃準確描述，要準確描述這些問題，必須引用基于Stackelberg博弈的雙層規劃來描述主體間的關系和各自利益的取舍。

根據產品性質及企業產品戰略的不同，模型的上層決策者和下層決策者有很多種組合種類。例如上層決策者為平臺效用，下層為產品參數決策；上層為平臺參數，下層為差異化參數；上層為模塊配置，下層為參數優化等。

Xia,Yi和Du Gang提出了二維矩陣模型完善了企業產品族主從關聯優化問題的提出。該模型用2個維度來描述：一個維度為產品族的層次，如平臺、產品、組件、供應鏈等；另一個維度為評價體系，如成本效益和技術指標等。通過箭頭連接二維象限上的點就可以清晰地導出一系列產品族主從關聯優化的問題。

1.2模塊配置-參數設計型產品族模型的構建

以模塊配置-參數設計產品族為例，其決策機制為平臺者決策產品族的模塊配置，參數決策者根據平臺決策者給定的模塊配置方案優化自身的參數選擇，這是一個典型的斯坦伯格博弈模型，運用雙層模型能表達其問題的實質。更進一步，由于產品族設計涉及多個產品及多個產品的多個屬性的設計，往往造成下層有多個決策者，且決策者有共享變量的情況，所以研究求解一主多從且從者帶有共享變量的雙層規劃問題(BLMFP with shared parameter)對于產品族理論在實際設計中的運用具有重要意義。

模塊配置-參數設計型的產品族主從優化模型是指上層決策者首先決策產品族各個模塊的選擇。模塊分為可選模塊和必選模塊，例如在計算機產品中，諸如顯示模塊、計算模塊及存儲模塊等是必須的，而發聲模塊、網絡連接模塊是非必須的。每個模塊都由若干個屬性來描述，而每一個屬性都可以分為若干個連續或離散的檔級。例如，計算機存儲模塊中可以包含容量大小、硬盤轉數、存儲介質等屬性，而每一個屬性如存儲空間大小又可以分為100GB、200GB等級別供選擇。

模塊配置和參數設計在本質上處于2個不同的層級，滿足主從關聯結構。尤其在本問題中，屬性參數的設計依賴于模塊配置的情況，處于相對從屬的地位，但其優化結果也會對模塊配置產生影響和約束，是交互的關系。兩者的優化目標也具有層級的區別，模塊配置是以整個產品族的利益為優化目標，一般會從企業競爭優勢的角度出發，追求目標市場的客戶利益最大化和企業利益最大化；而參數設計主要從本屬性的技術層面考慮，追求每個具體屬性的技術性能最優。綜上，運用雙層規劃模型描述模塊配置-參數設計型產品族問題是合適的。

本文模型為如下：

xjkl,yj∈{0,1}

s.t. hjk(Y,X,Zjk)=0

gjk(Y,X,Zjk)≥0

Gj(Y,X,ajk)≥0

j=1,…,J; k=1,…,K

(1)

模型的上層對模塊進行配置，對已知的J種可能的排列進行選擇，Y表示第j種產品方案Pj選擇變量，為1時表示選擇該產品，為0時表示不選擇該產品；令所有的y組成矩陣Y。xjkl表示Pj中k屬性l檔級的選擇變量，k=1,…,K，l=1,…,Lk。xjkl取值0或1,xjkl=1表示Pj中包括k屬性的l檔級；xjkl=0表示Pj中不包括k屬性的l檔級。令所有xjkl組成的矩陣為X。

上層采用效用和成品二者之比的形式，即單位成本的效用極大化作為上層規劃問題的目標函數，如式(2)所示。

(2)

上層的約束條件主要是產品族的選擇性要求，如產品族中的產品數量限制、兩種不同產品的差異性要求、產品對屬性檔級的擇一性要求。此外，還可根據情況增加一些特殊要求，如要求某屬性的某檔級必須選擇等。

模型的下層需要對各產品每一種屬性的技術參數設計進行決策，即對應于上層的模塊配置決策，設計使本屬性達到最優的技術參數。以zjkm表示j產品k屬性的第m個設計參數變量，j=1,…,J，m=1,…,mjk，k=1,…,K，則Zjk=(zjk1,…,zjkmjk)為下層第Jk模型的決策向量；Zjk與Xjk相對應，Xjk表示j產品k屬性中的檔級選擇，而Zjk表示在該檔級中進行優化的設計參數。設計參數變量一般來自工程領域中常見的變量，這根據問題的對象來相互區別。

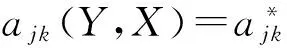
(3)

下層的約束條件可分為2類：一類是技術要求，如一些必要的技術指標，如功率、油耗、效率等，另一類是市場指標，如成本、利潤率、市場效用等。

總結模型1的幾個特點如下：

1) 模型為典型的值型雙層規劃問題，下層反饋自身的最優值給上層，含有0-1整數變量的非線性雙層規劃模型。

2) 模型的下層有多個決策者，且從者有關聯。

3) 模型的上層規劃問題的約束中不含下層的決策變量產品族設計中的其他優化問題往往也具有以上3種特性。

針對以上3種特性，可以將模型(1)簡化為數學模型：

其中yi和z是如下問題的解:

針對求解有以上特點的雙層規劃模型的交互式模糊算法， Wang和Wan在文獻[13]中提出了一個解決多個從者并且從者有關聯變量情形的交互式模糊算法，但該文中的算法面臨2個未解決的問題：

1) 針對下層規劃問題公用的關聯變量采用和一般變量相同的處理策略，沒有體現公共變量的特殊性。

2) 文中滿意度函數定義的方法較為簡單，當可行域較大，目標函數值跨度較大時會對求解效率產生影響。

本文基于已有文獻提出了一種改進的解，即主多從雙層規劃問題的交互式模糊算法。

2　算法的思想及解的分析

針對以下模型：

其中yi和z是如下問題的解:

其中yi和z是如下問題的解：

可以證明，上式等價于以下模型：

其中yi和z是如下問題的解:

(4)

(5)

針對每一個K繼續求解如下模型(6)：

(6)

可以得到上層規劃問題的隸屬度函數為：

針對每一個j=1,2,…,K且j≠i求解模型(7)：

(7)

上下層規劃問題的隸屬度函數確定后，可以構建如下的單層數學規劃模型：根據Sakawa等在文獻[8]中的方法，得到的上、下層滿意度函數構建為單層規劃模型見式(8)：

(8)

其中，α為上層決策者對于隸屬度的下界，然后定義文獻[2]提出的衡量上層決策者對于下層決策者的忍讓程度的變量δ。由于本文下層由多個決策者構成，為準確衡量上層決策者的忍讓情況，做如下定義：對于每一個模型(8)的解可得

同時，上層指明一個忍讓度最大值和最小值，分別為Δmin和Δmax，針對計算出的每一組δmin和δmax都有以下幾種可能情況：

1) Δmin<δmin<δmax<Δmax，解滿足終止條件，計算停止；

2)δmin>Δmax：當前忍讓度過大，令αnewα+ε，重新計算模型(8)；

3)δmax>Δmin：當前忍讓度過小，令αnewα-ε，重新計算模型(8)；

4) 若存在δi>Δmax，令αi=αi-ε，若存在δi<Δmax，則令αi=αi+ε重新計算模型(8)。

3　算法步驟

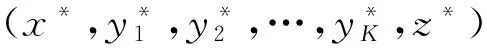
步驟5

1) Δmin<δmin<δmax<Δmax，解滿足終止條件，計算停止；

2)δmin>Δmax：當前忍讓度過大，令αnewα+ε，轉步驟4)；

3)δmax>Δmin：當前忍讓度過小，令αnewα-ε，轉步驟4)；

4) 若存在δi>Δmax，令αi=αi-ε，若存在δi<Δmax，則令αi=αi+ε,轉步驟4)。

4　算例

4.1模型介紹

本文以Simpson在其博士論文中提到的通用電機為對象。通用電器的電機產品廣泛運用在多個場合，小至攪拌機、電吹風，大到風力發電機，而不同的應用場合和與應用場景相關的不同技術規格具有明顯的產品族特性。本文在此運用產品族理論建立一個模塊配置即參數優化思想的產品族主從關聯優化模型，該模型最終歸結為一個一主多從的雙層規劃問題。

有關通用電機的設計參數主要包括電樞上的線圈繞數Nc、磁場中磁極的線圈繞數Nc、電樞線圈的橫截面積Awa(mm2)、磁極線圈的橫截面積Awf(mm2)、定子的外徑r0(cm)、定子的厚度t(cm)、堆棧長度L(cm)和電流I(A)。本案例考慮的通用電機產品族的8個設計變量的取值范圍分別為100≤Nc≤1 500，1≤Ns≤500，0.01≤Awa,Awf≤1，1≤r0≤10，0.05≤t≤1，0.1≤I≤6，0.057≤L≤5.18。一些給定的參數包括空氣槽長度lgap=0.07 cm，磁場中的極數pfield=2，銅電阻率ρ=1.69×10-8Ω·m，空氣槽長度lgap=0.07 cm，磁場中的極數pfield=2，銅電阻率ρ=1.69×10-8Ω·m，真空磁導率μ0=4π·10-7H/m，T0=0.05 N·m，鐵密度ρsteel=7.85 g/cm3，銅密度ρcopper=8.96 g/cm3，M0=2 kg。

根據模塊配置-參數設計產品族模型的理論，上層規劃問題對產品族中的產品進行選擇優化，下層規劃問題對每個產品的各個屬性進行優化，描述通用電機的屬性為：效率η、輸出功率P、電機扭矩T，其中效率、功率和扭矩表達式為(9)～(11)。

輸出功率P等于輸入功率Pin減去電阻造成的功率損耗：

P=(Vt-2)I-104·ρ·I2·

(9)

效率η等于輸出功率P除以輸入功率：

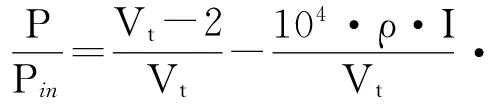
(10)

其中電壓Vt=115， P0=300W，Pin=Vt·I，空氣槽長度lgap=0.07cm，磁場中的極數pfield=2，銅電阻率ρ=1.69×10-8Ω·m。

扭矩T等于電機常數、磁通量和電流三者的乘積：

(11)

其中：真空磁導率μ0=4π·10-7H/m；T0=0.05 N·m。要確定上層規劃模型的具體表達式則要具體指明式中的參數和表達式。

通過聯合分析求得LSLT=500,β=170。同時綜合效用的表達式如(12)：

(12)

其中：ηL=0.6；ηU=0.8；PL=190；PU=240。

屬性檔級的效用值見表1。

表1　屬性檔級及其效用值

按照前文的敘述，下層規劃模型要對所有產品的效率，扭矩兩個屬性進行優化，表達式如下所示：

效率：

(13)

扭矩：

(14)

4.2運用交互式模糊算法的計算結果

整體模型為如式(14)：

(15)

w.r.t.Nc,Ns,Awa,Awf,r0,t,L,I*

s.t.P=P0

T≥T0

r0≥t

Zj1,Zj2∈R,j=1,…,J

為了減少問題規模，將下層的扭矩和功率加和作為參數優化的目標函數，這意味著一共有J種排列組合，便有J個下層規劃問題，下層變量中除了I*為下層共享變量外，其余變量都是從屬于自身規劃問題的獨立變量。

計算求解結果見表2。

表2　計算結果和及關鍵參數

5　結束語

本文針對產品族主從關聯優化模型的特色提出了一種基于交互式模糊算法框架的近似解法，成功解決了現有算法在面對下層多個規劃問題且規劃問題中含有公共決策變量的難點，在實際算例應用也中取得了良好的效果。但該算法還有諸多有待研究的地方，比如本文中確定容忍度上下限和是工程人員基于工程實際問題和經驗提出的，而更科學的做法應當是研究一種針對不同問題的結構化導出和的方法。另外，本文所描述的算法是將雙層規劃轉化為單層規劃，在最終求解的過程中還需運用現有的求解單層數學規劃的算法，所以研究一個針對產品族模型數學特色性質的單層規劃模型也是筆者將重點研究的方向。

[1]SHIH H S,LAI Y J,LEE E S.Fuzzy approach for multi-level programming problems[J].Computers & Operations Research,1996,23(1):73-91.

[2]SINHA S.Fuzzy programming approach to multi-level programming problems[J].Fuzzy Sets and Systems,2003,136(2):189-202.

[3]OSMAN M S,ABO-SINNA M A,AMER A H,et al.A multi-level non-linear multi-objective decision-making under fuzziness[J].Applied Mathematics and Computation,2004,153(1):239-252.

[4]VICENTE L,SAVARD G,JúDICE J.Descent approaches for quadratic bilevel programming[J].Journal of Optimization Theory and Applications,1994,81(2):379-399.

[5]EMAM O E.A fuzzy approach for bi-level intege1r non-linear programming problem[J]. Applied Mathematics and Computation2006,172:62-71.

[6]SAKAWA M,NISHIZAKI I.Interactive fuzzy programming for two-level linear fractional programming problems[J].Fuzzy Sets and Systems,2001,119(1):31-40.

[7]SAKAWA M,NISHIZAKI I.Interactive fuzzy programming for decentralized two-level linear programming problems[J].Fuzzy Sets and Systems,2002,125(3):301-315.

[8]SAKAWA M,NISHIZAKI I.Interactive fuzzy programming for two-level nonconvex programming problems with fuzzy parameters through genetic algorithms[J].Fuzzy Sets and Systems,2002,127(2):185-197.

[9]SAKAWA M,NISHIZAKI I,HITAKA M.Interactive fuzzy programming for multi-level 0-1 programming problems with fuzzy parameters through genetic algorithms[J].Fuzzy Sets and Systems,2001,117(1):95-111.

[10]SAKAWA M,NISHIZAKI I,UEMURA Y.Interactive fuzzy programming for multilevel linear programming problems[J].Computers & Mathematics with Applications,1998,36(2):71-86.

[11]SAKAWA M,NISHIZAKI I,UEMURA Y.Interactive fuzzy programming for multi-level linear programming problems with fuzzy parameters[J].Fuzzy Sets and Systems,2000,109(1):3-19.

[12]SAKAWA M,NISHIZAKI I,UEMURA Y.Interactive fuzzy programming for two-level linear fractional programming problems with fuzzy parameters[J].Fuzzy Sets and Systems,2000,115(1):93-103.

[13] WANG G,WANG X,WAN Z.A fuzzy interactive decision making algorithm for bilevel multi-followers programming with partial shared variables among followers[J].Expert Systems with Applications,2009,36(7):10471-10474.

(責任編輯劉舸)

Interactive Fuzzy Approach for Joint Optimization of Product Family Design

ZHANG Ru-chuan，DU Gang

(College of Management and Economics, Tianjin University, Tianjin 300072, China)

Under the industrial background of mass production, the theories about product family are hot research spot in recent years. Research considering the main body such as suppliers, assemblers and retailers in product family design phase is also increasing gradually. And instead of the static all-in-one optimization, many researchers take further step to deal with multi-agent problem inherited in the product family design on Stackelberg game perspectives. But those multi-follower bi-level programming problems always have complicated mathematic characteristics which the existing algorithms are unable to solve. In this paper, we introduced an approximating algorithm based on interactive fuzzy approach and a numerical example was provided to show its effectiveness on solving product family design problems.

product family design; bi-level programming; interactive fuzzy approach; Stackelberg

2016-01-26

國家自然科學基金項目“面向產品族設計與架構的主從關聯優化決策鏈及決策方法研究”(71371132)

張如川(1990—)，男，天津人，碩士，主要從事運籌學、工業工程、產品族架構與設計研究，E-mail:isaaczhang_tju@126.com。

format：ZHANG Ru-chuan，DU Gang.Interactive Fuzzy Approach for Joint Optimization of Product Family Design[J].Journal of Chongqing University of Technology(Natural Science)，2016(8):156-164.

10.3969/j.issn.1674-8425(z).2016.08.026

O22

A

1674-8425(2016)08-0156-09

引用格式：張如川，杜綱.面向產品族優化設計的交互式模糊算法[J].重慶理工大學學報(自然科學)，2016(8):156-164.