構形平面方法求解冗余機械臂逆運動學

魏延輝，韓寒，于園園，楊子揚

(哈爾濱工程大學 自動化學院，黑龍江 哈爾濱 150001)

?

構形平面方法求解冗余機械臂逆運動學

魏延輝，韓寒，于園園，楊子揚

(哈爾濱工程大學 自動化學院，黑龍江 哈爾濱 150001)

由于冗余機械臂存在冗余自由度, 導致其逆運動學求解方法復雜。本文依據構形平面的基本理論, 提出了一種快速、簡潔的冗余機械臂逆運動學求解方法。首先對冗余機械臂的結構進行分析, 將冗余機械臂分解成若干個構形平面。然后, 采用構形平面匹配方法, 將該機械臂工作構形進行位置和姿態匹配, 同時采用半解析的方式求得逆運動學解。 最后, 對7自由度冗余機械臂進行仿真計算, 實驗結果驗證了該方法求解精度高、求解速度快, 而且避免產生奇異值。

冗余機械臂；構形平面理論；逆運動學；空間矢量法；構形平面匹配；串聯機器人；半解析

網絡出版地址：http://www.cnki.net/kcms/detail/23.1390.u.20160624.1127.016.html

空間機械臂的末端位姿空間有6個變量，需要至少6個自由度以實現可達空間內的靈活控制。但是6自由度機械臂的一種末端位姿只對應有限組關節角空間的解，機械臂的操作靈活度不高[1-2]。相對于6自由度機械臂，冗余機械臂具有靈活度更高和避障性能更好的多方面的優點，但是逆運動學求解比較困難[3]。

在冗余機械臂的運動學解算問題已經進行了很多研究工作。文獻[1]采用幾何方法，運用特定的尋優指標，搜索與指定末端位姿對應的關節角空間最優解。文獻[3]采用加權最小范數法，推導出一種避免計算雅克比矩陣偽逆的優化方法。文獻[4-5]采用梯度投影算法，將機械臂之間的最大距離指標作為算法的優化目標函數。文獻[6]采用矢量逼近的控制算法，對冗余機器人系統的靈活性進行了研究。文獻[7]采用神經網絡方法，該方法能夠獲得運動學逆解，但是計算量龐大，而且算法的收斂和實時性作業限制該方法的應用。文獻[8]采用的幾何方法雖然精度高、計算快，但是其求解復雜，而且僅針對其對應的機器臂構形不具有通用性。文獻[9]以9自由度機器人為研究對象，提出了適于計算機迭代計算的冗余機器人在笛卡兒空間進行手爪姿態可變時的直線軌跡優化算法和手爪經過空間中任意不共線3點決定的平面內圓弧軌跡優化算法。文獻[10]提出一種二次計算的方法，運用梯度投影和固定關節組合的方式，提高計算的精度，但是計算量較大。文獻[11]利用改進的加權最小范數法求解冗余度機械臂的逆運動學。文獻[12]采用擴展雅克比的方法，將空間軌跡作為主要操作任務，而空間的姿態作為次級任務進而實現冗余機器人的運動學解算。文獻[13]采用了機器人位置和姿態進行分解方式，將7自由度的冗余機器人分解成4自由度的位置求解，再利用梯度投影法求解剩余關節的運動角度。但該方法損失了冗余機器人的靈活性能。文獻[14]提出一種平面冗余度機器人運動學自動尋優方法。文獻[15]采用螢火蟲群優化算法求冗余機械臂運動學逆解, 但該方法收斂速度慢。

本文針對冗余度機械臂的運動學求解方法進行研究，提出一種運用構形平面方法快速求解冗余機器人逆運動學方法，該方法不依賴機器人構形，形式簡單，降低了求解的難度，減少計算量，能夠按需要得到優化解，具有通用性和快速性。

1　構形平面

1.1機器人常用的工作構形

串行形式的機器人具有結構簡單、成本低、控制簡單、運動空間大等優點，在生產生活中應用最為廣泛。如搬運機器人、點焊機器人、噴涂機器人等。經典的串聯機器人機構如圖1所示。

圖1　典型的幾種工業機器人Fig.1　Several kinds of typical of industrial robots

從機器人機構學的運動穩定性、機構的整體設計和力學優化等方面因素考慮，串聯形式機器人連桿的中心軸線通常是共面的，如圖1(a)和圖1(b)所示。圖1(c)所示的機械臂，靈活度高，其工作構形的連桿中心軸線可拼成2～3個平面。圖1(d)所示的PUMA560的中心軸線平行于其他連桿組成的平面，這樣使得機器人關節的工作范圍變大。

1.2構形平面的引入

根據前文對機器人的工作構形特點分析，機器人三維空間機構可由機器人連桿中心軸線圍成的空間平面組成，復雜的空間運動學問題可轉化成二維平面構形問題。為此，在文獻[16]的可重構機器人運動學中引入了構形平面的概念，解決了一些機器人構形的運動學求解問題。對于如圖1(d)引入虛擬構形平面的概念。

定義1虛擬構形平面：串聯機器人結構中若干個連桿的中心軸線組成一個空間幾何平面，而其他的連桿的中心軸線平行該平面上，可以通過投影簡化的方法進行等效結構處理，形成的空間幾何平面稱為虛擬構形平面。

圖2(a)中的擺動關節1、2的關節軸線平行，連桿0和擺動關節1相連，擺動關節1、2之間是連桿1，把連桿1、2的中心軸線平移到連桿0所在的平面里(即虛擬構形平面處理)，如圖2(b)所示。通過虛擬構形平面處理，使得構形平面變成統一的形式，便于進行構形平面的匹配。多角度連接關節的運動學模型如圖3所示。

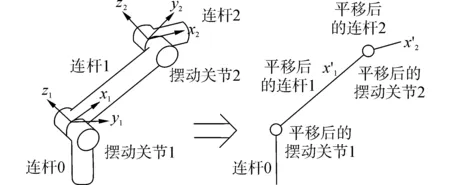
圖2　虛擬構形平面的平面化處理Fig.2　Plane processing on virtual configuration plane

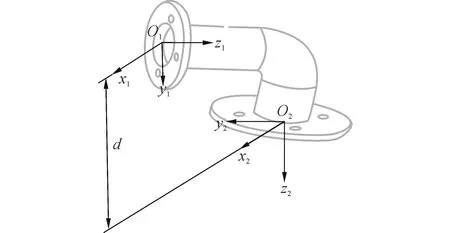
圖3　多角度連接關節運動學模型Fig.3　The kinematics model of link module with many connecting angles

按照文獻[16]中構形平面的定義，回轉關節可作為機器人工作構形劃分構形平面的依據。然而由于多角度連接關節的存在，使得機器人拓撲構形存在多樣性，在構形平面劃分時需要考慮這種連接關節。多角度形式的連接關節不具有運動能力，僅作為運動關節之間的連接，其運動學模型中沒有變量，圖3所示的是一個連接面繞x軸順時針轉動α角度的連接關節，建立其運動學數學模型:

(1)

式中d為多角度連接關節的結構參數。

1.3構形平面的表達形式

為便于構形平面匹配，需簡化其運動學模型。構形平面以角度連接關節和回轉關節進行區分。當角度連接關節的連接面的連接角度為0°或180°時，可通過虛擬構形平面的方式處理，使構形平面變成統一的形式，以便于進行構形平面的匹配；否則，該角度連接關節可以看作旋轉角固定的回轉關節，因此不能采用虛擬構形平面處理的方法，使得連桿在一個虛擬構形平面里。

一個通用形式的構形平面如圖4所示， P為該構形平面的構形平面中心, O為工作構形通過虛擬構形平面處理后的構形平面中心；若無需進行虛擬構形平面處理，O與P重合；Q為該構形平面的第1個搖擺關節的起始點， O與Q之間存在連接面繞y軸順時針轉動90°的連接關節，M與N之間存在連接面繞y軸逆時針轉動90°的連接關節，該構形平面由n+2個關節組成，Ja+i(i=0,1，…，n+1)為第i個關節的旋轉軸線，其中Ja+i(i=0,1，…,n)為搖擺關節旋轉軸線，與Q點坐標系的z軸平行；Ja+n+1為回轉關節旋轉軸線，與N點坐標系的z1軸平行。

圖4　構形平面的運動學模型Fig.4　Kinematics model of the configuration plane

經過虛擬構形平面平面化處理后的附加轉換矩陣:

(2)

該矩陣中px、py、pz分別為構形平面化處理后的構形平面中心補償的三維空間坐標值。

由式(1)可知，Q點和O點的連接面繞y軸順時針轉動90°的連接關節的數學模型用Tang_lOQ表示,d0為該連接關節的結構參數。

構形平面k中, 旋轉軸為Ja+i(i=0,1,…,n)的擺動關節或回轉關節的運動學模型為

(3)

式中θi(i=1,2,…,n+1)為轉動關節或擺動關節的旋轉角。

由于在構形平面k內的連桿關節是一般形式的連桿關節，即連接角度為0，則連桿i(i=1,2,…,n)數學模型用模型用Tli表示。構形平面內移動關節的數學模型用Tpi表示，di、li(i=1,2,…,n)分別是連接關節和移動關節的結構參數。

依次相連搖擺關節和移動關節組成的轉換矩陣為

(4)

式中:β=θ1+θ2…+θn,θi(i=1,2,…,n)為第i個搖擺關節轉動角度，

當第i個擺動關節與其相連的下一個關節不是移動關節時，li=0。否則的話li不等于零。

M點與N點間的連接面繞y軸逆時針轉動90°的連接關節的數學模型用Tang_lMN表示，p″y為該連接關節的結構參數。

定義

(5)

構形平面k末端點在二維空間相對P點坐標運動學簡化模型表達為

(6)

由式(6)可知，構形平面中，擺動關節、移動關節和連接關節完成構形平面的位置要求，擺動關節和回轉關節完成構形平面的姿態要求。

2　基于構形平面的運動學求解方法

2.1構形平面的劃分

根據文獻[16]定義的構形平面和上述引入的虛擬構形平面的特點，我們知道在冗余機器人拓撲結構中，其工作構形由若干個構形平面組成，如圖5所示，其中關節a是回轉關節，關節b是多角度連接關節。回轉關節和多角度連接關節是區分構形平面的依據。組成機器人工作構形的構形平面的個數小于機器人的自由度數，通過對構形平面內和構形平面間的關節進行運動學分析，可以快速求得可冗余機器人的逆運動學解。

圖5　構形平面組成的冗余機器人工作構形Fig.5　The work configuration of redundant robot composed of configuration planes

設目標點的位姿矩陣TS為

(7)

2.2構形平面的位置解算

由式(6)可知，構形平面中的擺動關節、移動關節和連接關節完成構形平面的位置要求，構形平面終點在構形平面起點坐標系下的空間坐標為

(8)

目標點的空間坐標為

(9)

在位置解算時，首先把機器人構形看成一個構形平面，由式(7)可得

(10)

由式 (10)可以求得構形平面內的β(即所有擺動關節的轉動角之和)的值。

采用如下的方法求θi(i=1,2,…，n-1) (即構形平面內第i個擺動關節的轉動角)的值。

對于如圖6所示的一般形式的構形平面，采用基于矢量投影的方法進行自動求解，既滿足：

(11)

式中：‖p‖為末端矢量的范數；ki為第i個關節桿臂在矢量p上投影與該關節桿臂的比值，由于矢量投影具有方向性，因此ki具有正負號，其表達式為

(12)

圖6　構形平面的二維空間一般形式Fig.6　Two-dimensional space of the general form of the configuration plane

如果兩個構形平面中有一個構形平面的工作空間固定，則這個構形平面的匹配點的空間坐標值就是一定的，經過構形轉化后，可直接用矢量投影法求解構形平面內關節的關節變量。如果兩個構形平面的工作空間都是不確定的，按照前一個構形平面承擔位置要求，后一個構形平面進行位置補充的原則，進行構形平面的位置匹配。

在多構形平面的位置匹配上，關鍵是在各關節的運動范圍內找到構形平面間的位置匹配點。按照構形平面工作空間的表示方法，在目標點和基坐標系原點連線的空間矢量上，找到構形平面間的匹配點，這樣構形平面的位置匹配就確定了。

2.3構形平面的姿態解算

由于構形平面內的擺動關節和回轉關節完成構形平面內的姿態要求，上文已完成構形平面的位置解算，因此在構形平面的運動學模型里只有一個參數是未知的，即回轉關節的關節角。假如在冗余機械臂的拓撲結構中，存在多個構形平面，則需要進行多個構形平面的姿態匹配。把通過構形平面位置解算求得的擺動關節的關節角之和β代入式(5),則TH為已知量。

設4個構形平面組成冗余機械臂的工作構形，由式(7)得

(13)

在式(13)中，THi(i=1,2,3,4)是已知量，使得式(13)中等式兩邊矩陣的前三列前三行元素對應相等，即可求得回轉關節的關節角，完成姿態解算。

值得說明的是，這里所求的各關節角值還需要進行校驗，考查是否超出各關節角的運動范圍，如超出，需在構形平面的位置解算部分重新計算，進而直接調整其他關節角。

實際計算中，由于三角函數計算存在多解的狀態，需要進行選取確定。

3　實例驗證

3.1冗余機械臂數學建模

以文獻[3]設計的冗余機械臂作為研究對象，如圖7所示。該機械臂由3個運動關節組成：肩、肘、腕。具有7個自由度，肩關節由3個自由度，肘關節有2個自由度，腕關節也有2個自由度，按照人體構造設計。各關節運動范圍如表1所示。

由于冗余機械臂可簡化成7自由度的連桿結構，桿件之間由旋轉關節連接，每個旋轉關節為一個獨立自由度，完成單軸旋轉運動[17]。采用模塊化的建模方法，將各個關節進行分解成單自由度關節形式，模型如圖7所示。冗余機械臂的結構參數如表1所示。

表1　冗余機械臂的關節運動范圍和連桿參數

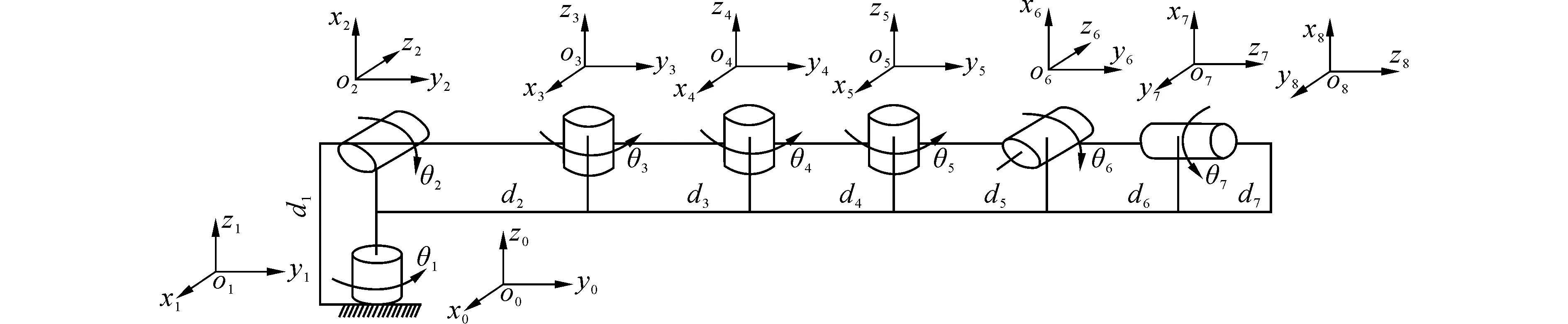
圖7　冗余機械臂運動學模型Fig.7　Kinematics model of redundant manipulator

基于模塊建模方法，各關節運動學模型如下：

(14)

式中：θi是第i(i=1,2，…,7)個關節的關節變量，關節1和關節2之間是多角度形式的連桿，其運動學模型為

(15)

關節2和關節3之間是多角度形式的連桿，其運動學模型為

(16)

關節3、4、5之間是一般形式的連桿，其運動學模型為

(17)

(18)

關節5和關節6之間是多角度形式的連桿，其運動學模型為

(19)

關節6和關節7之間是多角度形式的連桿，其運動學模型為

(20)

冗余機械臂末端的運動學模型為

(21)

冗余機械臂目標點的位姿矩陣如下：

(22)

3.2構形平面的劃分

根據冗余機械臂的工作構形參數可知，參數d1和d6都為0，意味著O1和O2，O6和O7是兩兩重合的，而由于結構的原因，O1和O2相對機械臂原點坐標的位置是固定的，而O6和O7相對機械臂末端點的位置也是固定的。因此在進行機械臂運動學求解時，關節1、2、6、7主要承擔機械臂末端的姿態要求。關節3、4和5的轉動軸是相互平行的，其中心軸線組成一個二維空間的平面，因此這三個關節滿足機械臂空間位置要求。

按照構形平面的定義，回轉關節作為劃分構形平面主要依據，而該機械臂的工作構形中還存在多角度連接關節，如連接關節12、23、56和67。把回轉關節1看成構形平面1，連接關節12和關節2組成構形平面2，關節3、4、5、6和連接關節23、34、45、56組成構形平面3，連接關節67和關節7組成構形平面4。由式(6)得

(23)

(24)

(25)

(26)

式(26)中

(27)

3.3構形平面的位置解算

由式(7)可知：

(28)

由于d7是已知的，因此T8是已知的，設TG6=TS·T8-1，把式(22)代入式(28)得

(29)

于是

(30)

由于d1、d6為0，則O1、O2與O0重合,O6與O7重合，可知構形平面3承擔冗余機械臂末端位置解算。

可知構形平面3的中點即點O6的空間坐標為

(31)

因此構形平面3的起點即O2到構形平面3的中點即點O6長度L為

(32)

在構形平面3中，已知L長度，按照矢量投影的方法，由于是多解的狀態，也沒有空間避障的要求，而且構形平面3中的3個關節角都沒有超出運動范圍，因采用3個關節運動角度相等的方式進行求解，易得

(33)

3.4構形平面的姿態解算

把式(33)代入式(26)，可得

(34)

把式(34)代入式(30)，在式(30)中，使得等式兩邊矩陣對應位置的元素相等，可依次求得各關節的關節變量。因此冗余機械臂的逆運動學解如下：θ1=-11.45°、θ2=34.72°、θ3=15.20°、θ4=15.20°、θ5=15.20°、θ6=-9.04°、θ7=17°。

該方法避免了冗余機械臂在逆運動學求解過程中出現的奇異值，而且采用半解析的方式，求解精度更高，求解速度更快。

4　結論

1) 本文通過分析總結串聯機器人工作構形的特點，引入虛擬構形平面的概念，并提出了構形平面理論。進而采用構形平面方法解決冗余機械臂的逆運動學問題。

2) 冗余機械臂的拓撲結構可分解為若干個構形平面，通過對構形平面進行建模和匹配，實現冗余機械臂工作構形的位置和姿態匹配。這鐘方法使得復雜的機械臂拓撲結構簡單化，而且得到的逆運動學解中避免了奇異解的產生。

3) 采用半解析的方式，使得該方法形式簡潔，具有很高的精度和求解速度，因此具有很強的實用性和通用性。而且構形平面的方法為冗余機械臂的運動學優化、軌跡規劃、空間避障任務奠定了基礎。

[1]陳鵬, 劉璐, 余飛, 等. 一種仿人機械臂的運動學逆解的幾何求解方法[J]. 機器人, 2012, 34(2): 211-216.

CHEN Peng, LIU Lu, YU Fei, et al. A geometrical method for inverse kinematics of a kind of humanoid manipulator[J]. Robot, 2012, 34(2): 211-216.

[2]PRIMROSE E J F. On the input-output equation of the general 7R-mechanism[J]. Mechanism and machine theory, 1986, 21(6): 509-510.

[3]陽方平, 李洪誼, 王越超, 等. 一種求解冗余機械臂逆運動學的優化方法[J]. 機器人, 2012, 34(1): 17-21, 31.YANG Fangping, LI Hongyi, WANG Yuechao, et al. An optimization method for solving the inverse kinematics of redundant manipulator[J]. Robot, 2012, 34(1): 17-21, 31.

[4]馬如奇, 王偉東, 董為, 等. 基于改進梯度投影算法的腹腔微創外科手術機器人系統術前擺位分析[J]. 機器人, 2014, 36(2): 156-163.

MA Ruqi, WANG Weidong, DONG Wei, et al. Preoperative positioning analysis of the celiac minimally invasive surgery robotic system based on an improved gradient projection algorithm[J]. Robot, 2014, 36(2): 156-163.

[5]DUBEY R V, EULER J A, BABCOCK S M. Real-time implementation of an optimization scheme for seven-degree-of-freedom redundant manipulators[J]. IEEE transactions on robotics and automation, 1991, 7(5): 579-588.

[6]張秋豪, 孫漢旭, 魏世民. 改善冗余度機器人靈活性的研究[J]. 北京郵電大學學報, 2004, 27(4): 74-77, 101.

ZHANG Qiuhao, SUN Hanxu, WEI Shimin. A new method for improving flexibility of redundant robot[J]. Journal of Beijing University of Posts and Telecommunications, 2004, 27(4): 74-77, 101.

[7]XIA Youshen, WANG Jun. A dual neural network for kinematic control of redundant robot manipulators[J]. IEEE transactions on systems, man, and cybernetics, part B: cybernetics, 2001, 31(1): 147-154.

[8]MOHAMED H A F, YAHYA S, MOGHAVVEMI M, et al. A new inverse kinematics method for three dimensional redundant manipulators[C]//ICCAS-SICE. Fukuoka, 2009: 1557-1562.

[9]賈慶軒, 褚明, 孫漢旭, 等. 9-DOF超冗余機器人軌跡規劃優化算法[J]. 北京郵電大學學報, 2008, 31(2): 20-25.

JIA Qingxuan, CHU Ming, SUN Hanxu, et al. Research on the optimal algorithm for trajectory planning of a 9-DOF hyper-redundant robot[J]. Journal of Beijing University of Posts and Telecommunications, 2008, 31(2): 20-25.

[10]祖迪, 吳鎮煒, 談大龍. 一種冗余機器人逆運動學求解的有效方法[J]. 機械工程學報, 2005, 41(6): 71-75.

ZU Di, WU Zhenwei, TAN Dalong. Efficient inverse kinematic solution for redundant manipulators[J]. Chinese journal of mechanical engineering, 2005, 41(6): 71-75.

[11]JIA Qingxuan, HONG Lei, SUN Hanxu. An improved algorithm for inverse kinematics solution of redundant modular robots[C]//Proceedings of the International Technology and Innovation Conference. Hangzhou, 2006: 2087-2092.

[12]謝宗武, 孫奎, 劉宏. 擴展雅克比方法的冗余度機器人逆運動學應用[J]. 哈爾濱工業大學學報, 2009, 41(5): 34-37.

XIE Zongwu, SUN Kui, LIU Hong. Application study on inverse kinematics algorithm of redundant manipulator based on extended Jacobian method[J]. Journal of Harbin Institute of Technology, 2009, 41(5): 34-37.

[13]潘博, 付宜利, 楊宗鵬, 等. 面向冗余機器人實時控制的逆運動學求解有效方法[J]. 控制與決策, 2009, 24(2): 176-180.

PAN Bo, FU Yili, YANG Zongpeng, et al. Efficient inverse kinematics solution for redundant robots to realtime control[J]. Control and decision, 2009, 24(2): 176-180.

[14]霍希建, 劉伊威, 姜力, 等. 平面冗余自由度機器人自尋優運動優化方法[J]. 哈爾濱工程大學學報, 2015, 36(4): 528-533.

HUO Xijian, LIU Yiwei, JIANG Li, et al. Self-optimizing kinematic optimization method of planar redundant robots[J]. Journal of Harbin Engineering University, 2015, 36(4): 528-533.

[15]羅天洪, 陳才, 李富盈. 基于時變螢火蟲群算法的冗余機器人手臂逆解[J]. 計算機集成系統, 2016, 22(2): 576-582.

LUO Tianhong, CHEN Cai, LI Fuying. Inverse solution of redundant robot arm based on glowworm swarm optimization algorithm of time-varying[J]. Computer integrated manufacturing systems, 2016, 22(2): 576-582.

[16]魏延輝, 趙杰, 高延濱, 等. 一種可重構機器人運動學求解方法[J]. 哈爾濱工業大學學報, 2010, 42(1): 133-137. WEI Yanhui, ZHAO Jie, GAO Yanbin, et al. A solution method for kinematics of reconfigurable modular robots[J]. Journal of Harbin Institute of Technology, 2010, 42(1): 133-137.

[17]ASFOUR T, REGENSTEIN K, AZAD P, et al. ARMAR-Ⅲ: An integrated humanoid platform for sensory-motor control[C]//Proceedings of the 6th IEEE-RAS International Conference on Humanoid Robots. Piscataway, NJ, USA, 2006: 169-175.

本文引用格式：

魏延輝，韓寒，于園園，等. 構形平面方法求解冗余機械臂逆運動學[J]. 哈爾濱工程大學學報, 2016, 37(8): 1096-1102.

WEI Yanhui, HAN Han, YU Yuanyuan, et al. Solving inverse kinematics for redundant manipulator using configuration plane method[J]. Journal of Harbin Engineering University, 2016, 37(8): 1096-1102.

Solving inverse kinematics for redundant manipulator using configuration plane method

WEI Yanhui, HAN Han, YU Yuanyuan, YANG Ziyang

(College of Automation, Harbin Engineering University, Harbin 150001, China)

Due to the redundancies in the redundant manipulator, its inverse kinematics solution is complex. In this paper, based on the basic configuration plane theory, we propose a method for generating a rapid and concise solution to the inverse kinematics of the redundant manipulator. First, we analyzed the structure of the redundant manipulator and decomposed it into several configuration planes. Then, using the configuration plane matching method to match the position and orientation of the manipulator’s working configuration, we obtained the semi-analytic inverse kinematics solution. Finally, based on the results from a numerical simulation experiment for a 7-DOF redundant manipulator, we verified that the proposed method is fast, generates a highly precise solution, and avoids singular values.

redundant manipulator; configuration plane theory; inverse kinematics; space vector; configuration plane matching; serial robot; semi-analysis

2015-06-26.網絡出版日期：2016-06-24.

國家自然科學基金項目(51205074)；國家科學技術部國際科技合作項目(2014DFR10010);高等學校博士點基金項目(20112304120007)；中央高校基本科研業務費(HEUCF160403).

魏延輝(1978-), 男, 碩士生導師；

韓寒(1990-), 女,博士研究生.

韓寒, E-mail: hanhan979063996@163.com.

10.11990/jheu.201507059

TG156

A

1006-7043(2016)08-1096-07