用R實現GARCH模型的估計
賈慧琴
西安財經學院陜西
用R實現GARCH模型的估計
賈慧琴
西安財經學院陜西
隨著股票市場規模的不斷擴大,股票市場的不確定性也隨之加劇,為了研究股票市場的發展狀況。本文選取深證A指2011 年4月1日至2016年4月1日的日收益率數據為研究對象,針對其收益率序列,建立時間序列模型,結果表明,GARCH(5,0)模型能夠較好的擬合深證A指日收益率序列。
GARCH;日收益率;深證A指
1.文獻綜述
早在 20 世紀 60 年代就有學者對股票市場收益率波動性進行了研究,并且Mandlebrot(1963)率先發現了這種收益率波動的聚集性特征。并且對于股票收益率波動的研究我國許多學者也進行了相關研究。如陳艷,韓立磊(2009)利用ARCH 族模型對滬深 300 指數進行實證研究,分析滬深股票市場近年日收益率波動的相關特性。本文選取深證A指2011年4月1日至2016年4月1日的日收益率數據為研究對象,針對其收益率序列,建立時間序列模型,結果表明,GARCH(5,0)模型能夠較好的擬合深證A指日收益率序列。
2.模型簡介
2.1 ARMA模型的定義
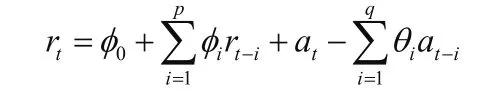
2.2 自回歸條件異方差模型
2.2.1 ARCH模型的定義
傳統的經濟計量模型假設樣本方差不隨時間改變。為了改進這些模型,Engle (1982)提出了一類新的隨機過程模型,稱為自回歸條件異方差模型,用以捕捉金融數據的時變性與聚類特征.ARCH模型如下:
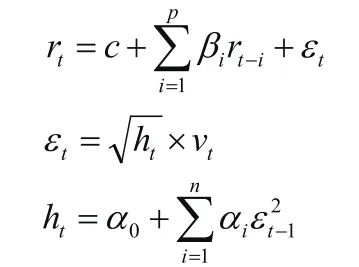
由上式可以看出ARCH模型實質是使用 的p階移動平均擬合當期異方差函數值,由于移動平均模型具有自相關系數p階截尾性,因此ARCH模型實際上只適用于異方差函數短期自相關過程。
2.2.2 ARCH效應的檢驗
記at=rt-ut為均值方程的殘差,則可以用平方序列來檢驗條件異方差性,即所謂的ARCH效應。有兩個檢驗可以用,第一個檢驗是將通常的Ljung-Box統計量應用于序列,該假設的原假設是序列前m個間隔的ACF值都為零。第二個對條件異方差的檢驗是Engle(1982)的拉格朗日乘子檢驗。
2.3 GARCH模型
在實踐中,有些殘差序列的異方差函數是具有長期自相關性的,這時如果使用ARCH模型擬合異方差函數,將會產生很高的移動平均階數,這會增加參數估計的難度并最終影響ARCH模型的擬合精度。
1986年,Bollerslev提出的廣義ARCH模型,即GARCH模型,克服了ARCH模型的一些缺點,將GARCH模型運用在金融時間序列上能夠更有效地捕捉條件方差的動態特征,從而簡化高階的ARCH模型,其具體形式是將ARCH模型中方差方程擴展為:
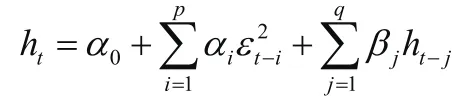
如果將條件方差引入均值方程中,即有以下形式:
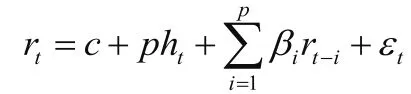
表示將預期收益與預期風險緊密聯系在一起,原因在于人們一般認為金融資產的收益應當與其風險成正比,風險越大,預期的收益就越高。這種利用條件方差表示預期風險的模型被稱為ARCH均值方程或ARCH-M回歸模型。根據條件方差方程的形式不同,還可以有GARCH-M回歸模型。如果將虛擬變量引入條件方差方程,即有以下形式:
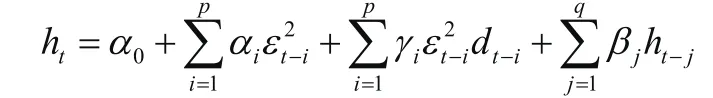
其中,dt-i為虛擬變量,當時εt<0時,dt-i=1,否則dt-i=0。這個模型被稱為TGARCH模型,引入虛擬變量的作用是衡量好消息(εt>0)和壞消息(εt<0)對條件方差的不同影響,好消息有一個a的沖擊,而壞消息有一個a+γ的沖擊。如果γ≠0,則信息是非對稱的,反之,則信息是對稱的。另外,GARCH模型的擴展形式還有PGARCH模型、EGARCH模型等。
3.數據來源及檢驗分析
本文選取深證A指2011年4月1日至2016年4月11日的日收益率,共1216個數據為研究對象,數據來源于銳思金融數據庫系統,統計分析軟件為R-3.2.3。
3.1 平穩性檢驗和平穩化處理
通過深證A指日收益率時序圖可以看出,深證A指日收益率的波動沒有明顯的趨勢或波動,基本可以視為平穩序列。用R畫出樣本ACF和PACF圖,由樣本ACF和PACF圖建立ARMA(1,1)模型。并且檢驗發現ARMA(1,1)模型滿足顯著性條件,說明模型擬合良好。
3.2 ARCH效應檢驗
通常通過L-B統計量檢驗來判定是否存在ARCH效應。通過檢驗結果可以看出,序列的Q(m)統計量給出的Q(30)=63.362,p值為0.000354,說明數據沒有序列相關性。at序列的Ljung-Box統計量Q(30)=1289.8,p值接近于零,這表明存在很強的ARCH效應。下面就來進行ARCH階數識別和建模。
3.3 ARCH階數識別
通過作圖可以清楚地看出,深證A指具有5階ARCH效應,對于高階的ARCH效應,我們通常采用廣義的ARCH模型也就是通常所說的GARCH模型。
3.4 建立模型
根據上述模型的估計的p值可得其系數都高度顯著,說明ARMA(1,1)-GARCH(5,0)模型擬合效果較好。
最后,確定模型:
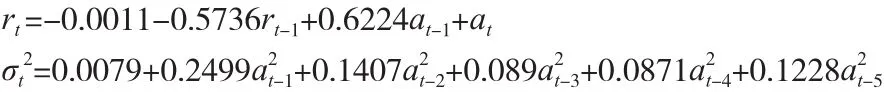
4 結論
本文選取深證A指2011年4月1日至2016年4月1日的日收益率數據為研究對象,針對其收益率序列,利用GARCH模型對深證A指日收益率序列進行了實證研宄,所用軟件為R。首先對深證A指日收益率數據進行了基本統計特征分析,平穩性分析,ARCH效應檢驗,發現深證A指指數序列平穩。ARCH 效應分析時,檢驗結果都顯示殘差序列具有ARCH效應,然后進行建模。結果表明,ARMA(1,1)-GARCH(5,0)模型能夠較好的擬合深證A指日收益率序列。建模過程中發現,市場的波動性具有的持續性,而且當收益率受到異常波動的沖擊時,在短期內很難消除其影響,所以金融市場具有很大的投資風險。由這些金融數據的特點,我們可以為投資者提供躲避風險以及為應對風險提供可靠地決策依據。
[1]Benoit Mandelbrot.The Variation of Certain Speculative Prices[J].Journal of Business,1963,36(4):115-130.
[2]Engle R F..Autoregressive Conditional Heteroskedasticity with Estimates of the VARiance of United Kingdom Inflation[J].Econometrica,1982,50(7):203-224.
[3]Bollerslev.T.Generalized regressive conditional heteroskedasticity[J].Journal of Econometrics,1986,31(8):307-327.
賈慧琴(1992-)女,漢族,甘肅平涼人,碩士研究生,研究方向:非線性動力學與統計學

