基于遞推最小二乘法的永磁伺服系統參數辨識

荀　倩　王培良　李祖欣　蔡志端　秦海鴻

(1.湖州師范學院工學院　湖州　313000 2.南京航空航天大學江蘇省新能源發電與電能變換重點實驗室　南京　211100)

?

基于遞推最小二乘法的永磁伺服系統參數辨識

荀倩1王培良1李祖欣1蔡志端1秦海鴻2

(1.湖州師范學院工學院湖州313000 2.南京航空航天大學江蘇省新能源發電與電能變換重點實驗室南京211100)

為使永磁同步電機(PMSM)控制系統在復雜環境中具有較好的動態性能，伺服系統必須具有參數辨識和參數自整定的功能，而轉動慣量與負載轉矩辨識是其首要解決的問題。采用零階保持器對電機運動方程進行離散化建模，考慮了摩擦系數對辨識結果的影響，將基于遺忘因子遞推最小二乘辨識算法應用于該離散模型可以同時辨識出系統轉動慣量、負載轉矩和摩擦系數。同時，針對Matlab/Simulink中庫模型參數不能在線動態修改的缺點，提出改進型PMSM模型，以此搭建了伺服系統的仿真控制模型，完成了定參數與變參數的動態仿真。最后，在stm32微控制器上進行了實驗驗證。仿真和實驗表明該文提出的電機離散化模型和參數辨識方法具有一定的準確性和實時性，仿真結果驗證了改進型PMSM模型在變參數仿真研究中的實用性。

永磁同步電機動態性能參數辨識離散模型遺忘因子遞推最小二乘法

0　引言

永磁同步電機(Permanent Magnet Synchronous Motor，PMSM)由于結構簡單、運行可靠、功率密度大、效率高等優點，易于構成高性能的伺服系統，被廣泛應用于家用電器、交通工具、工業控制等各個領域[1]，在電力拖動系統中具有重要的應用價值。而永磁同步電機是集電氣與機械為一體的部件，機械在運動中會受到諸多無法預知因素的影響，如外界負載擾動、摩擦力擾動或系統參數變化等[2]。這些擾動會直接或間接影響系統精度、穩定性以及動靜態特性。

電機運行中，隨著電機運行工況的變化，系統負載轉矩和轉動慣量也隨之改變。當負載轉矩增加或減小時，由于傳統PI調節器本身屬于一種誤差調節，必然導致轉速調節的滯后，在負載突變的較短時間內導致轉速跌落或上升；而當電機轉動慣量增加時，會使系統調節時間增加，出現不穩定，引起爬升現象，當電機轉動慣量減小時，雖然會減小系統動態調節時間，但會使電機轉速出現超調甚至振蕩現象[3]。為了提高系統的動態抗擾性能，需要相應地調整調節器控制參數，使系統運行特性為最佳狀態，而轉動慣量和負載轉矩辨識是其首要研究的問題。

近年來，國內外學者對永磁伺服系統的參數辨識進行了許多研究，主要用到減速法、人工軌跡規劃法、轉矩限幅加速度法[3，4]等離線辨識方法。該類方法得到的參數估計值精度較高，且對計算時間要求不是很嚴格，但在電機傳動負載過程中，由于運行工況的變化，整個系統的負載轉矩、轉動慣量或其他參數會隨時改變，采用離線辨識方法得到的伺服系統參數是一個靜態的估算值，不能反映系統參數的動態變化。因此，國內外許多學者在離線辨識的基礎上，將現代控制理論、系統辨識理論等應用于參數辨識中，提出了各種在線辨識方法，包括最小二乘法、自適應朗道離散時間法、擴展卡爾曼濾波法、參數估計梯度校正法、蟻群算法、狀態觀測器法等[5-13]。

文獻[5，6]提出了基于朗道離散時間法的轉動慣量辨識算法。其中文獻[5]采用降階觀測器對負載轉矩進行了辨識，但朗道離散時間算法和降階觀測器收斂時間較長，且轉動慣量和負載轉矩的辨識不能同時實現。文獻[7]利用遺傳算法設計了一種系統參數辨識的方法，可以同時估算出電機定子電阻、dq軸電感和永磁體磁鏈，仿真和實驗結果表明4個待辨識參數均能在較短時間內收斂，且其魯棒性較好。文獻[8]提出了一種定階頻域經驗最優參數估計算法(Fixed-order Empirical Frequency-domain Optimal Parameter Estimation，FOEFOP)，對電機轉動慣量進行了辨識，仿真和實驗說明了FOEFOP算法在慣量辨識方面不受負載擾動和系統采樣周期影響，辨識精度高，具有較強魯棒性。文獻[9]對永磁同步電機電阻及電感等參數進行了辨識，在此基礎上設計了電流調節器，實現了永磁同步電機的自適應控制。文獻[3]在傳統離線辨識方法的基礎上，提出了改進型的加減速算法、二分法及模型參考自適應辨識法，對各種辨識算法進行了對比分析。文獻[10，11]分別提出了蟻群辨識算法與轉動慣量辨識的誤差補償算法，其對參數辨識精度的改善具有重要的指導意義。文獻[12，13]采用帶遺忘因子的遞推最小二乘法對永磁同步電機定轉子電感和漏電感進行了辨識，并采用基于瞬時無功功率模型的自適應方法對定轉子電阻進行了辨識，具有一定的實用價值。文獻[14]提出了一種基于模型參考自適應理論的辨識方法，在同一模型中可以辨識出表貼式PMSM的定子電阻、交直軸電感和永磁體磁鏈等多個參數，具有實用性。

以上文獻在進行電機轉動慣量辨識時的離散化建模上忽視了摩擦系數對辨識結果的影響。本文考慮了摩擦系數，引入零階保持器對電機的運動方程離散化，將基于遺忘因子遞推最小二乘方法應用于該模型，可同時辨識出系統轉動慣量、負載轉矩和摩擦系數，搭建了Matlab/Simulink仿真模型，對伺服系統的定參數辨識和變參數辨識進行了仿真研究。在進行變參數仿真時，針對Simulink中庫模型參數不能在線動態修改的不足提出了改進型PMSM模型。

1　最小二乘法理論

最小二乘法最早是由高斯(K.F.Gauss)在形體運動軌道預報研究工作中提出的，此后，其成為參數辨識理論的奠基石，被廣泛應用于系統辨識和參數估計中[15]。

1.1遞推最小二乘法

(1)

式中，Φ為數據向量矩陣；Y為系統輸出矩陣。

批處理最小二乘法在每次處理數據時需要計算矩陣的逆，尤其是當尾數較大時，計算量較大，因此需要采用遞推最小二乘法。

遞推最小二乘法的思想為

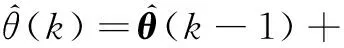
(2)

由此可得k時刻的批處理最小二乘估計為

(3)

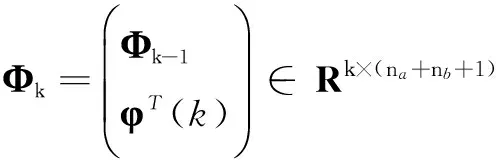
令協方差矩陣P(k)為

=[P-1(k-1)+φ(k)·φT(k)]-1

(4)

由此可得

P-1(k)=P-1(k-1)+φ(k)·φT(k)

(5)

由式(3)、式(4)可推算出k-1時刻的估算值為

(6)

由式(5)、式(6)可得

(7)

于是k時刻的最小二乘估計可表示為

(8)

式中，K(k)為增益向量，K(k)=P(k)φ(k)。

由矩陣求逆引理與式(8)可得遞推最小二乘法的迭代公式為

(9)

1)得到L組數據(L>na+nb+1)后，利用批處理最小二乘法計算

(10)

2)直接令

(11)

式中，α可以取充分大的正實數，一般為104～106；ε可以取充分小的正的實向量或零向量。

1.2遺忘因子遞推最小二乘法

由于隨著處理數據的增加，遞推最小二乘法將出現“數據飽和”現象。為防止這種現象的發生，一般采用帶遺忘因子的遞推最小二乘法，對性能指標做出一定修正。

設目標函數J為

(12)

式中，λ 為遺忘因子，0<λ≤1。

根據式(12)，對照遞推最小二乘法的推導過程可得帶遺忘因子遞推最小二乘法參數估算的迭代公式為

(13)

通常遺忘因子λ 的取值范圍一般為 0.9 ≤λ ≤1。若λ =1，則式(13)即為遞推最小二乘法的迭代公式。

2　辨識算法實現

2.1電機運動方程

在電氣傳動中，電機通過其傳動軸向負載提供電磁轉矩，對負載運動的控制也就是對電機傳動軸上電磁轉矩的控制，電機帶動負載的傳動系統如圖1所示。

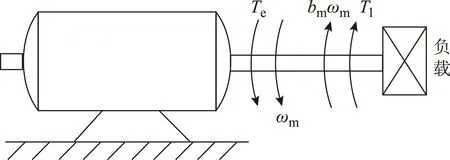
圖1　電機及其負載Fig.1　The motor and its load

根據動力學原理，可得永磁同步電機的機械運動方程為

(14)

式中，Te為電磁轉矩；J為系統轉動慣量；ωm為轉子機械角速度；bm為摩擦系數；Tl為負載轉矩，其包含由電機空載損耗產生的電機空載轉矩。

2.2運動方程離散化

對式(14)進行拉氏變換得

Te(s)-Tl(s)=bmωm(s)+Jsωm(s)

(15)

令y(s) =ωm(s)，u(s)=Te(s)-Tl(s)，則可得電機運動方程的傳遞函數為

(16)

零階保持器的傳遞函數為

(17)

因為

(18)

帶有零階保持器的開環系統脈沖傳遞函數為

(19)

即

(20)

因此，電機運動方程可離散化為

ωm(k)-e-bmTc/Jωm(k-1)=

(21)

令b=-e-BmTc/J，a=(1+b)/Bm，c=aTl(k-1)， 則式(21)可轉換為

REUBROYCHAROEN Prasert（1980-），男，博士，教授，博士生導師，主要從事多相催化與化學反應工程研究。

ωm(k)=aTe(k-1)-bωm(k-1)+c·(-1)

(22)

輸出y(k)=ωm(k)，φT(k)=[Te(k-1)，-ωm(k-1)，-1]， θ=[a，b，c]T， 則有

y(k)=φT(k)·θ

(23)

Tc為辨識算法的控制周期，由于Tc很小，所以采樣頻率很高，可近似忽略離散化帶來的失真，由高等數學中極限的知識可將a、b、c簡化為

(24)

對應最小二乘法遞推算法公式得

(25)

3　PMSM慣量辨識控制框圖

根據式(13)和式(25)可以得到伺服系統參數辨識的程序流程如圖2所示。

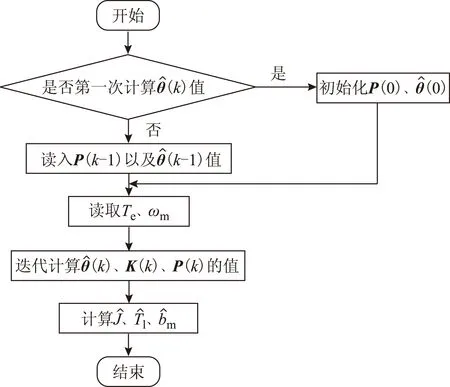
圖2　辨識器的程序流程Fig.2　The program flow chart of the identifier

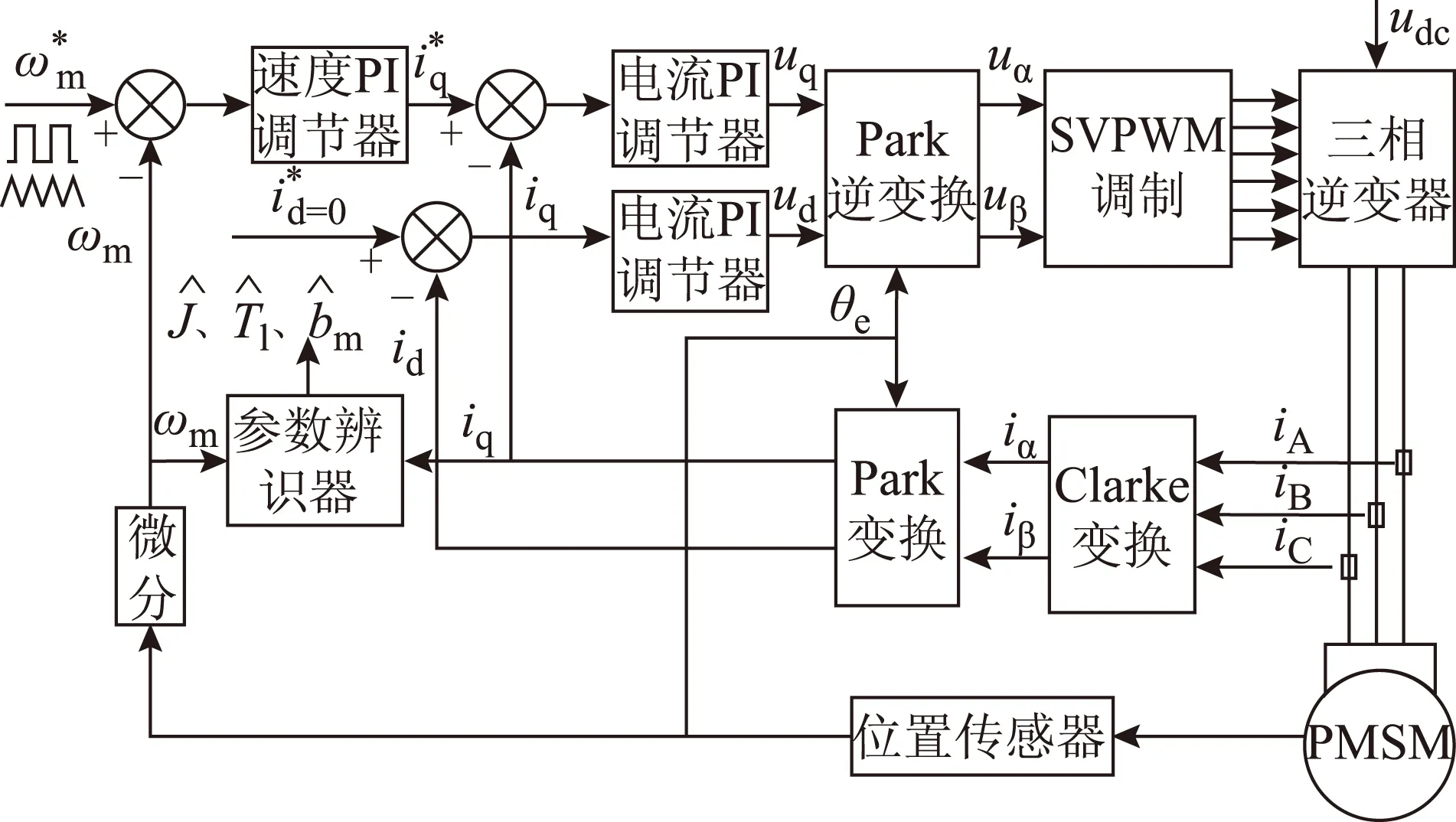
圖3　伺服系統慣量辨識框圖Fig.3　The inertia identification block diagram

4　仿真與實驗

在Matlab2013/Simulink環境下搭建如圖3所示的PMSM雙閉環矢量控制系統。PMSM的轉子轉動慣量標稱值Jm=0.915×10-3kg·m2，摩擦系數bm=3.035×10-4N·m·s。當電機空載起動時，負載轉動慣量為0，總轉動慣量即為電機轉子轉動慣量，則伺服系統的轉動慣量J =Jm=0.915×10-3kg·m2。

4.1仿真驗證

4.1.1定參數仿真

為了測試伺服系統在恒定轉動慣量、恒定負載條件下遺忘因子λ 對辨識結果的影響，仿真中分別取λ為1和0.98，對遞推最小二乘法和帶遺忘因子的遞推最小二乘法進行了仿真，系統轉動慣量J =Jm=0.915×10-3kg·m2，負載轉矩Tl=0N·m，其仿真結果如圖4和圖5所示。

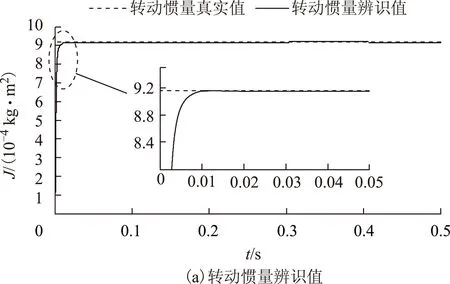
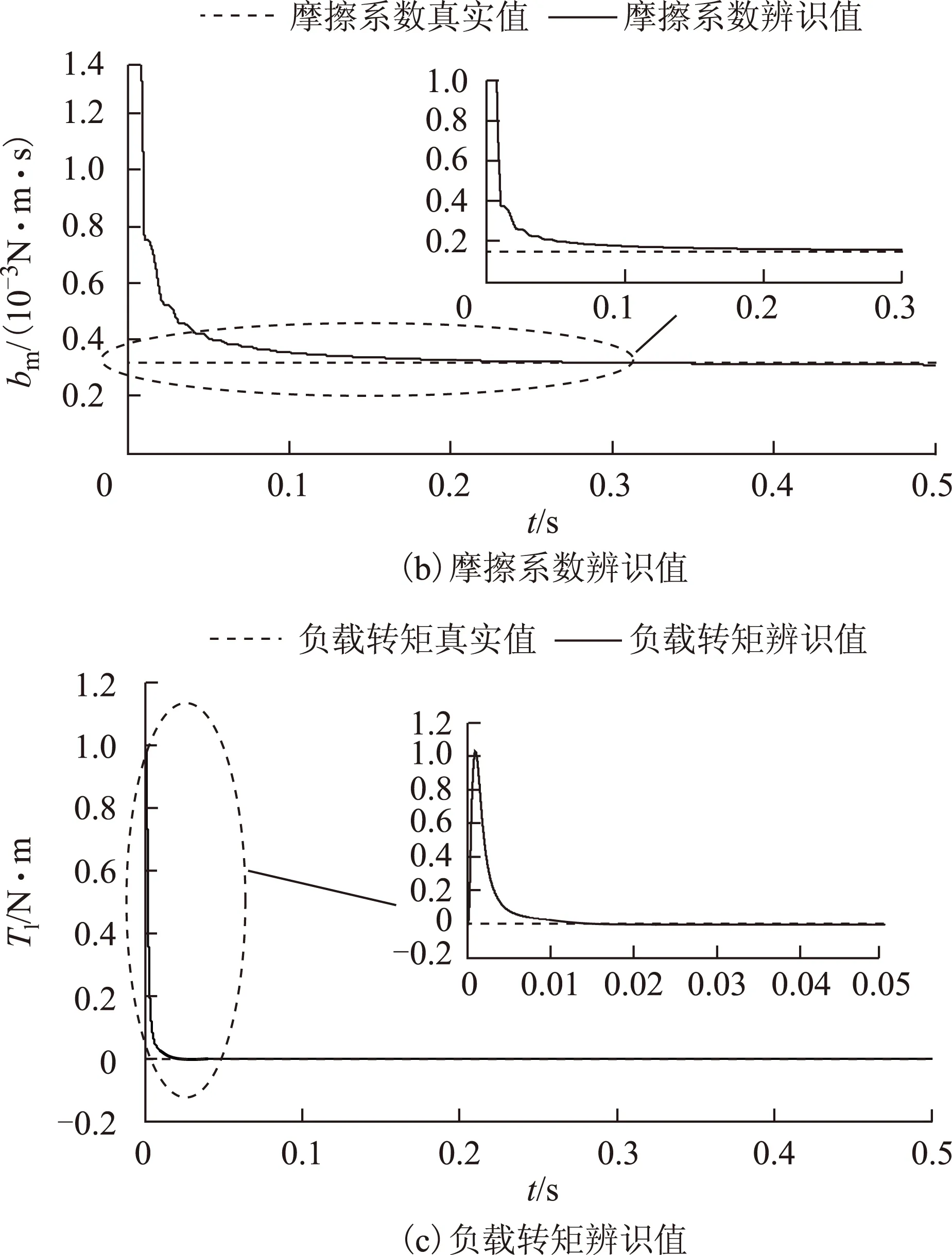
圖4　λ為1時的辨識結果Fig.4　The identification results when λ is equal to 1

由圖4可以看出，當λ取1時，轉動慣量和負載轉矩的辨識值基本上可以在0.02s時收斂為真實值，而摩擦系數的辨識收斂時間較長為0.2s，總收斂時間為0.2s。圖5表明λ取0.98時，轉動慣量、摩擦系數和負載轉矩的辨識值均可在0.002s內收斂為真實值，并且對轉動慣量、摩擦系數和負載轉矩的辨識更加準確，因此帶遺忘因子的遞推最小二乘法辨識收斂速度更快，辨識精度更高。

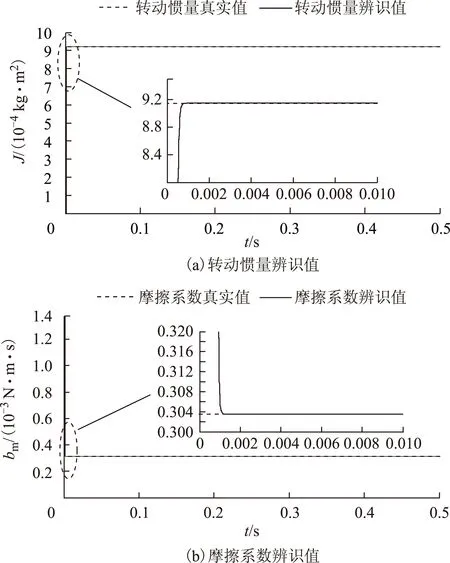
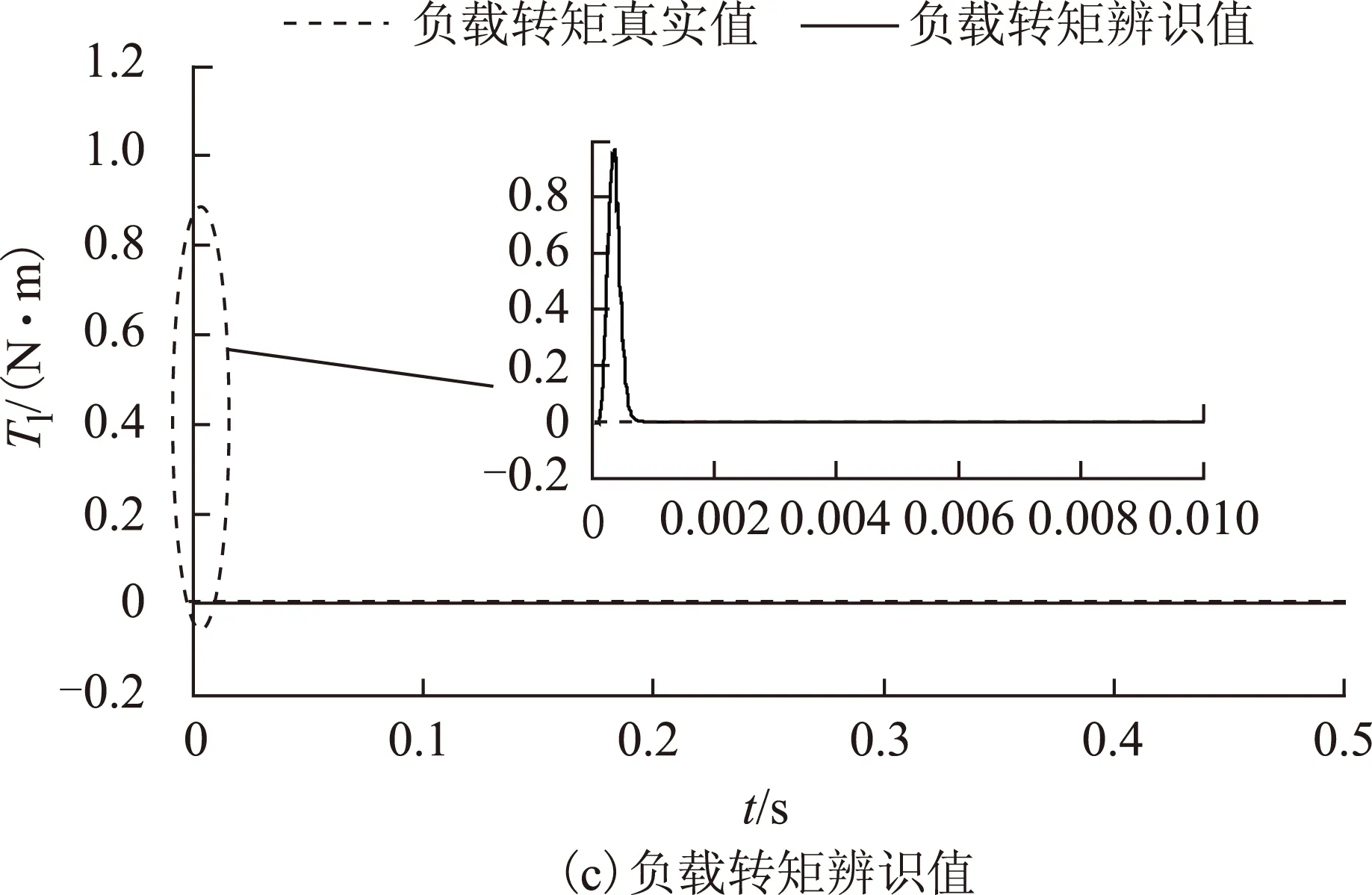
圖5　λ為0.98時的辨識結果Fig.5　The identification results when λ is equal to 0.98

4.1.2變參數仿真

由于Simulink中集成PMSM模塊的轉動慣量參數只能在仿真運行前通過靜態框離線設置，而變慣量仿真需要在線修改轉動慣量值以模擬其隨運行工況的變化。為使原有PMSM模型中的轉動慣量可以在線動態修改，可以采用兩種方法：①根據PMSM數學模型創建自定義模型；②根據需求修改庫文件模型，然后再重新封裝[16]。而前者在自定義模型創建過程中，對PMSM電機的數學建模做了一些近似處理，會造成與實際模型差別較大，且自定義搭建模型工作量較大，因此本文采用第二種方法對庫文件模型進行修改。

由于系統原有的PMSM組件在封裝好之后是處于鎖定狀態的，用戶不能直接修改底層模塊，因此首先需要在解鎖狀態下，對庫文件中PMSM模型中的底層模型進行修改，找到需要修改的模塊替換成預想模型，再將其更新到仿真中。圖6為修改后的PMSM封裝圖。仿真時，J端口可接入任何常量或變量信號，以實現參數的在線修改。在電機運行過程中，摩擦系數的變化量較小，其變化可忽略不計，而在電機負載轉矩不變或變化時，轉動慣量都有可能變化。因此，以下是在遺忘因子λ為0.98的情況下，對電機的變慣量和變負載轉矩的仿真。

圖6　改進后的PMSM封裝Fig.6　PMSM package improved

首先分析電機負載轉矩Tl=0N·m，當系統轉動慣量J按照Jm、2Jm、5Jm、10Jm的連續階躍信號變化時，辨識結果如圖7所示。由仿真波形可見，在仿真時間t =0.1s、0.2s、0.3s時刻，轉動慣量的真實值發生階躍跳變，轉動慣量的辨識值均在0.002s內跟蹤真實值的變化，較為準確地識別出轉動慣量值，而負載轉矩的辨識會在轉動慣量突變瞬間有一定影響，但會在0.001s內恢復。

在電機負載轉矩Tl=0N·m的情況下，當系統轉動慣量按照J =[2 +sin(20πt)]Jm的正弦規律變化時，辨識結果如圖8所示。轉動慣量的辨識值可以很快跟蹤轉動慣量真實值的變化，但轉動慣量真實值變化頻率較快，導致負載轉矩辨識值一直在0N·m附近波動。

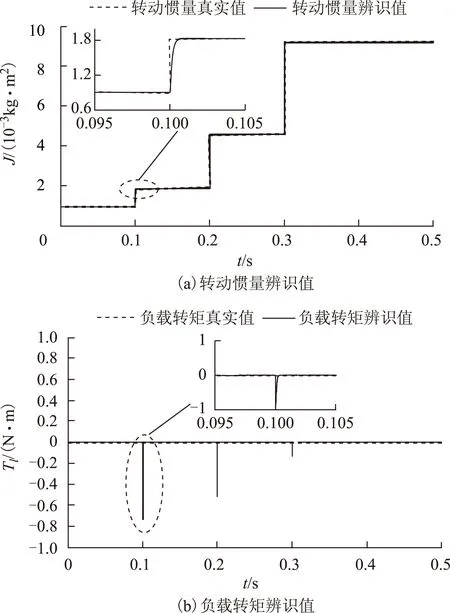
圖7　空載時階躍轉動慣量的辨識結果Fig.7　Identification results of step inertia without load

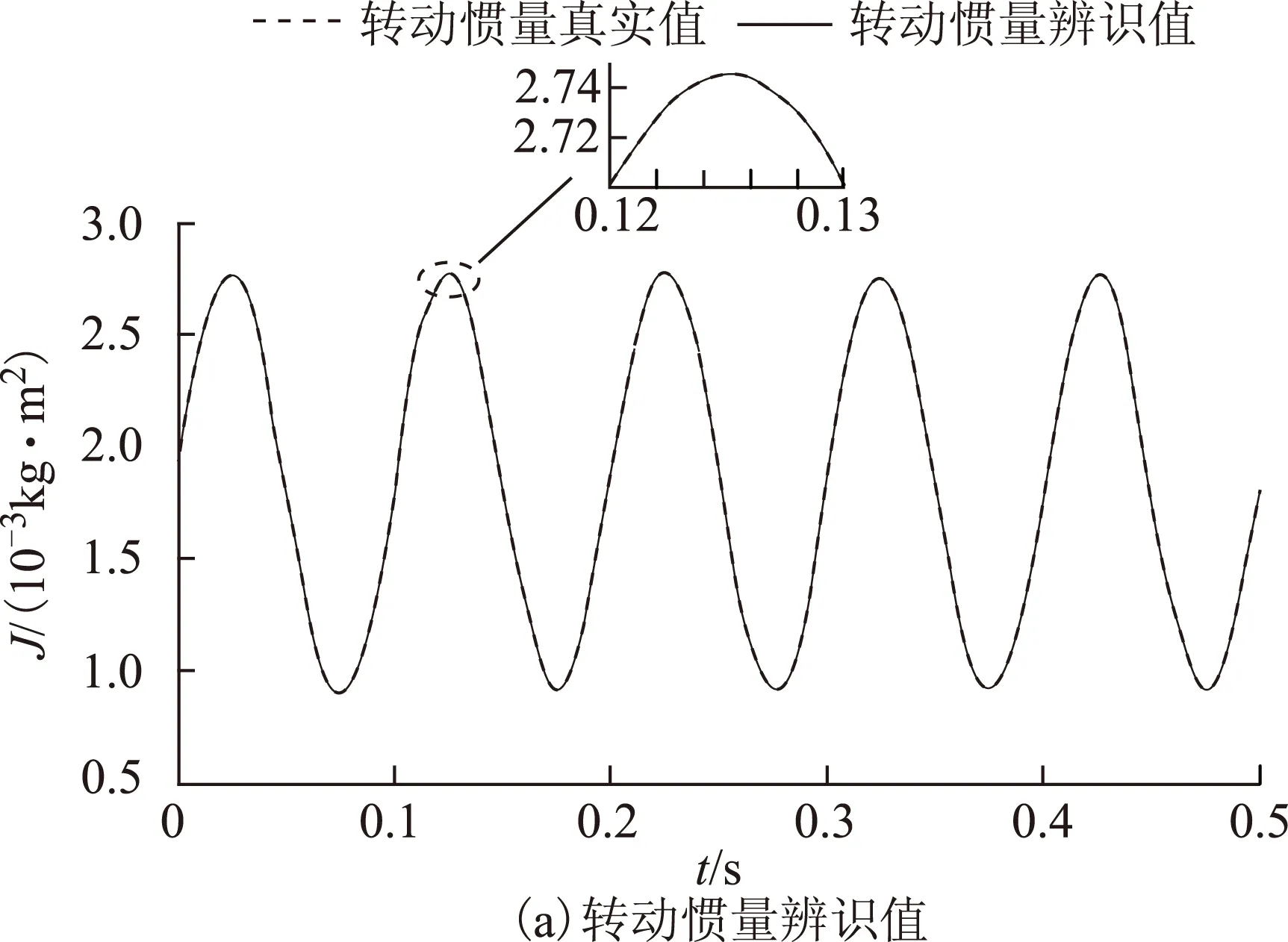
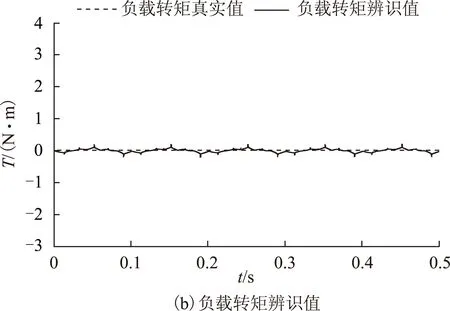
圖8　空載時正弦轉動慣量的辨識結果Fig.8　Identification results of sine inertia without load

當電機負載轉矩Tl在仿真時間t =0.1s、0.2s、0.3s時刻從0N·m連續變化為1N·m、2N·m、5N·m，而相應的系統轉動慣量J按照Jm、2Jm、5Jm、10Jm的連續階躍信號變化時，辨識結果如圖9所示。轉動慣量和負載轉矩可以在0.002s內跟隨給定值變化。

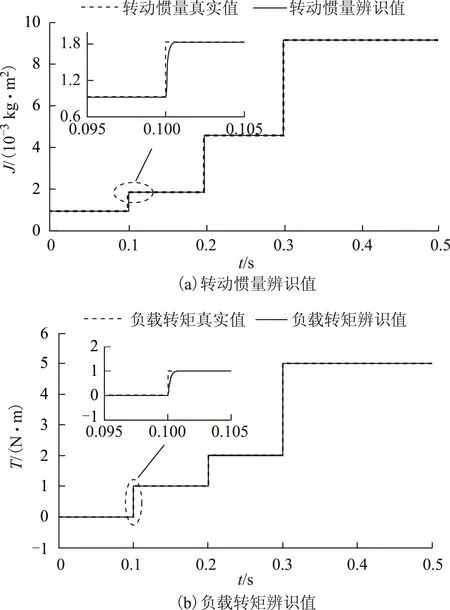
圖9　階躍負載、階躍轉動慣量時辨識結果Fig.9　Identification results of step inertia with step load

以上辨識結果表明，改進型的PMSM模型可以在線動態修改模型參數，帶遺忘因子的最小二乘辨識算法收斂時間短，辨識精度高。

4.2實驗驗證

為驗證本文提出的離散化模型與辨識方法的有效性，搭建基于stm32f103rc芯片的參數辨識測試平臺，其由磁滯測功機、聯軸器、永磁同步電機、控制器、調壓器、示波器和計算機構成，實驗系統如圖10所示。

圖10　參數辨識測試平臺Fig.10　Test platform of parameter identification

為驗證本文方法的辨識性能，首先在空載條件下進行負載轉矩與轉動慣量辨識，辨識算法同時用到電磁轉矩和電機轉速，在實際系統中，電機轉速的計算周期為500ms，辨識周期Ts不能小于轉速計算周期的最大值。因為若辨識周期過小，在一個周期內電磁轉矩的采樣存在一定噪聲，干擾辨識結果，這將導致辨識結果不穩定；但是辨識周期也不能太大，在一個周期內，電機的加速度可能發生變化，電機運動方程的離散化模型和實際有偏差，模型的不準確會給辨識算法帶來誤差，經實驗調試，辨識周期取1ms。

為了方便觀察算法的收斂過程，本文將Tl、Ts/J作為轉動慣量辨識結果的觀測量。在實際應用中，電機一般會處于頻繁起停工況，因此實驗中轉速給定為階躍信號，為使電機有充裕時間加速到給定轉速，轉速給定周期為500ms，轉速在300～600r/min之間變化的梯形波。

圖11為空載條件下的參數辨識結果。轉動慣量和負載轉矩可以在6s內收斂，其辨識值分別為0.915×10-3kg·m2、0N·m，辨識結果準確。

圖11　空載條件下參數辨識結果Fig.11　Parameter identification results under no load condition

為驗證變參數條件下的辨識結果，空載時辨識結果收斂之后突加2N·m負載的實驗波形如圖12所示。空載時，負載轉矩收斂值為0N·m，轉動慣量收斂值為1.387×10-3kg·m2(該轉動慣量值為電機本體轉動慣量與聯軸器、測功機轉動慣量之和)，突加2N·m負載，負載轉矩和轉動慣量辨識值分別在5s內收斂為2N·m和1.965×10-3kg·m2。

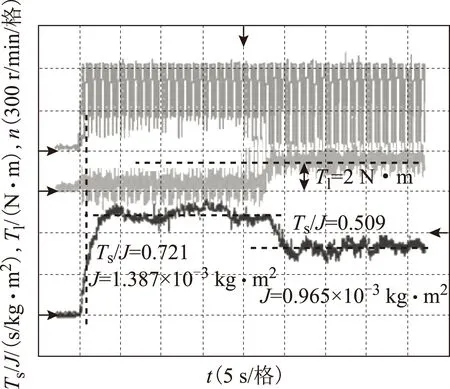
圖12　加載條件下參數辨識結果Fig.12　Parameter identification results under load condition

5　結論

目前，大部分的轉動慣量辨識模型忽略了摩擦系數對辨識結果的影響。本文在進行電機運動方程離散化建模時考慮了摩擦系數，設計了基于遺忘因子遞推最小二乘法的伺服系統參數辨識方法，可以同時辨識出轉動慣量、摩擦系數和負載轉矩。并針對Simulink集成模塊不能進行參數動態修改的缺點，通過修改庫文件模型來彌補集成模型的不足，提出了改進型PMSM模型。仿真與實驗表明辨識器辨識速度快，辨識誤差小，具有較好的跟蹤特性，同時，仿真驗證了改進模型的正確性。本文對Simulink庫模型中PMSM模塊的修改方法適用于其他庫模型的修改，改進的PMSM模型在時變參數辨識中具有較大的實用價值。基于遺忘因子最小二乘辨識算法可應用于電機其他參數的辨識，以便更好地監控電機運行。

[1]DuttaR，RahmanMF.Designandanalysisofaninteriorpermanentmagnet(IPM)machinewithverywideconstantpoweroperationrange[J].IEEETransactionsonEnergyConversion，2008，23(1)：25-33.

[2]ZhangDongyu，DevoreCE，JohnsonEA.Responsemodificationtoimprovetheparameteridentificationofshearstructures：anexperimentalverification[J].IEEE/ASMETransactionsonMechatronics，2013，18(6)：1683-1690.

[3]孫昊，王茂海，齊霞.基于PMU實測數據的同步發電機參數在線辨識方法[J].電力系統保護與控制，2014，42(3)：31-36.SunHao，WangMaohai，QiXia.SynchronousgeneratorparametersidentificationbasedonPMUdata[J].PowerSystemProtectionandControl，2014，42(3)：31-36.

[4]BarcellonaS，CiccarelliF，IannuzziD，etal.Modelingandparameteridentificationoflithium-ioncapacitormodules[J].IEEETransactionsonSustainableEnergy，2014，5(3)：785-794.

[5]魯文其，胡育文，梁驕雁，等.永磁同步電機伺服系統抗擾動自適應控制[J].中國電機工程學報，2011，31(3)：75-81.

LuWenqi，HuYuwen，LiangJiaoyan，etal.Anti-disturbanceadaptivecontrolforpermanentmagnetsynchronousmotorservosystem[J].ProceedingsoftheCSEE，2011，31(3)：75-81.

[6]張占學.基于最小二乘法的pH值溫度補償模型[J].電氣技術，2015，16(2)：115-117.

ZhangZhanxue.ResearchofpHvaluetemperaturecompensationmodulebasedontheleastsquaresmethod[J].ElectricalEngineering，2015，16(2)：115-117.

[7]肖曦，許青松，王雅婷，等.基于遺傳算法的內埋式永磁同步電機參數辨識方法[J].電工技術學報，2014，29(3)：21-26.

XiaoXi，XuQingsong，WangYating，etal.Parameteridentificationofinteriorpermanentmagnetsynchronousmotorsbasedongeneticalgorithm[J].TransactionsofChinaElectrotechnicalSociety，2014，29(3)：21-26.

[8]NiuLi，XuDianguo，YangMing，etal.On-lineinertiaidentificationalgorithmforPIparametersoptimizationinspeedloop[J].IEEETransactionsonPowerElectronics，2015，30(2)：849-859.

[9]王少威，萬山明，周理兵，等.利用蟻群算法辨識PMSM伺服系統負載轉矩和轉動慣量[J].電工技術學報，2011，26(6)：18-25.

WangShaowei，WanShanming，ZhouLibing，etal.IdentificationofPMSMservosystem’sloadtorqueandmomentofinertiabyantcolonyalgorithm[J].TransactionsofChinaElectrotechnicalSociety，2011，26(6)：18-25.

[10]徐東，王田苗，魏洪興.一種基于簡化模型的永磁同步電機轉動慣量辨識和誤差補償[J].電工技術學報，2013，28(2)：126-131.XuDong，WangTianmiao，WeiHongxing.Asimplifiedmodelbasedinertiaidentificationalgorithmwitherrorcompensationofpermanentmagnetsynchronousmotors[J].TransactionofChinaElectrotechnicalSociety,2013，28(2)：126-131.

[11]陽同光，桂衛華.基于粒子群優化神經網絡觀測器感應電機定子電阻辨識[J].電機與控制學報，2015，19(2)：89-95.

YangTongguang，GuiWeihua.Statorresistanceidentificationforinductionmotorbasedonparticleswarmoptimizationneuralnetworkobserver[J].ElectricMachinesandControl，2015，19(2)：89-95.

[12]趙海森，杜中蘭，劉曉芳，等.基于遞推最小二乘法與模型參考自適應法的鼠籠式異步電機轉子電阻在線辨識方法[J].中國電機工程學報，2014，34(30)：5386-5394.

ZhaoHaisen，DuZhonglan，LiuXiaofang，etal.Anon-lineidentificationmethodforrotorresistanceofsquirrelcageinductionmotorsbasedonrecursiveleastsquaremethodandmodelreferenceadaptivesystem[J].ProceedingsoftheCSEE，2014，34(30)：5386-5394.

[13]GautierM，VentureG.Identificationofstandarddynamicparametersofrobotswithpositivedefiniteinertiamatrix[C]//2013IEEE/RSJInternationalConferenceonIntelligentRobotsandSystems，Tokyo，2013，5815-5820.

[14]楊宗軍，王莉娜.表貼式永磁同步電機的參數在線辨識[J].電工技術學報， 2014，29(3)：111-118.

YangZongjun，WangLina.OnlineMulti-parameteridentificationforsurface-mountedpermanentmagnetsynchronousmotors[J].TransactionsofChinaElectrotechnicalSociety，2014，29(3)：111-118.

[15]LiGuoqi，WenChangyun.Identificationofwienersystemswithclippedobservations[J].IEEETransactionsonSignalProcessing，2012，60(7)：3845-3852.

[16]王莉娜，楊宗軍.SIMULINK中PMSM模型的改進及在參數辨識中的應用[J].電機與控制學報，2012，16(7)：77-82.

WangLina，YangZongjun.PMSMmodel’sreforminSIMULINKandapplicationinparameters’identification[J].ElectricMachinesandControl，2012，16(7)：77-82.

PMSM Parameters Identification Based on Recursive Least Square Method

Xun Qian1Wang Peiliang1Li Zuxin1Cai Zhiduan1Qin Haihong2

(1.School of EngineeringHuzhou UniversityHuzhou313000China 2.Jiangsu Key Laboratory of New Energy Generation and Power Conversion Nanjing University of Aeronautics and AstronauticsNanjing211100China)

The permanent magnet servo control system must have features of parameter identification and parameter self-tuning to get better dynamic performance in a complex environment.Among them，the identification of inertia and load torque has the first priority.In this paper，the zero-order holder is introduced to discretize the motion equation of the motor.And the influence of the friction coefficient on the identification results is taken into consideration.The inertia，the load torque，and the friction coefficient can be identified simultaneously using the recursive least square method with a forgetting factor.In the Matlab/Simulink library model，the parameters cannot be modified on-line dynamically.So the improved PMSM model is proposed.Then the servo system simulation control model is built up.The constant and the variable parameters of dynamitic simulation are conducted.Finally，the experiments are carried out on the stm32 micro controller.The simulation and experimental studies show that the motor discrete model and the parameter identification method proposed in the paper have a certain accuracy and real-time property.The simulation results show the usefulness of the improved PMSM model in the variable parameter simulation study.

Permanent magnet synchronous motor，dynamic performance，parameters identification，discrete model，recursive least squares method with a forgetting factor

2015-02-22改稿日期2015-05-20

TM351

荀倩女，1990年生，碩士，研究方向為參數辨識、電機控制、功率變換器。

E-mail：xunq520@hotmail.com(通信作者)

王培良男，1963年生，教授，研究方向智能控制、系統辨識。

E-mail：wpl@zjhu.edu.cn

國家自然科學基金(61573136，61573137)和湖州市公益性技術應用研究計劃項目(2015GZ05)資助。