導管式推進器非定常性能數值計算方法研究

舒禮偉（海軍裝備部，北京 100841）

導管式推進器非定常性能數值計算方法研究

舒禮偉
（海軍裝備部，北京 100841）

基于滑移網格方法，采用SST k-ω 湍流模型研究不同網格劃分方式對帶前置定子導管式推進器非定常性能的研究。首先基于相對參考坐標系法及滑移網格方法分別對推進器在定常與非定常下的性能進行數值預報，并與試驗結果相比驗證計算方法的可靠性。基于該方法研究整體網格劃分方式與周期性網格對推力系數、扭矩系數與推進器各個方向上的非定常脈動力的影響。研究結果為進一步研究推進器非定常性能提供了參考。

滑移網格；推進器；周期性網格；非定常力

0　引 言

工作在艇后的推進器會產生周期性脈動的非定常力，周期性脈動非定常力是激發推進器線譜噪聲的噪聲源，它的預報和分析是優化推進器噪聲性能的前提，同時也是預報推進器線譜噪聲的基礎。對推進器非定常力進行數值預報要求能夠較為準確地捕捉到推進器較大的推力總量和微小的脈動量，目前已經能較為準確地對推進器定常下的性能分析，對推力值的數值分析精度已能滿足工程需求［1］，但是微小的推力脈動量的準確捕捉相對較困難，該方面的研究也相對較少。

隨著 CFD 技術的快速發展，近年來許多學者致力于研究螺旋槳非定常性能數值計算方法。譚廷壽和熊鷹等［2-3］采用速度勢面元法對螺旋槳非定常性能進行了數值預報，通過與試驗值的對比驗證了計算方法的可靠性。胡小菲等［4］采用滑移網格方法對孤立螺旋槳在給定的非均勻伴流場下的非定常力進行數值分析，研究了整體網格尺度對非定常結果的影響，沈海龍和姚震球等［5-6］將螺旋槳與船體作為一個整體，基于滑移網格方法研究了螺旋槳與船體之間的非定常干擾特性，結果表明船體對螺旋槳的影響主要是尾流場的非均勻性改變了螺旋槳的進流速度，螺旋槳對船體的影響主要是改變了船體表明的壓力分布。

工作于艇后的推進器與螺旋槳工作環境類似，但是推進器模型與螺旋槳有所差別，推進器模型由導管、前置定子及轉子等組成，非定常性能也將發生變化，目前對推進器非定常性能的研究很少。本文基于SST k-ω 湍流模型，采用滑移網格方法導管式推進器模型的非定常力數值計算方法，并對不同網格劃分方式對推進器非定常性能的影響進行研究。

1　計算方法

1.1計算模型與網格

計算模型采用文獻［7］中 Hughes 設計的帶前置定子的導管式推進器，定子采用 NACA 63-018 翼型，葉片數為 9，轉子翼型采用 NACA a=0.8（mod），葉片數為 4，z 軸指向出口，計算模型及坐標系設置如圖1所示。整個流場計算域為圓柱體，入口距螺旋槳盤面位置約 6 倍螺旋槳直徑，以保證來流速度到達時均勻，出口距螺旋槳盤面位置約 7 倍螺旋槳直徑，以保證尾流充分發展，圓柱體直徑約為 4 倍螺旋槳直徑，以保證計算結果不受邊界的影響。

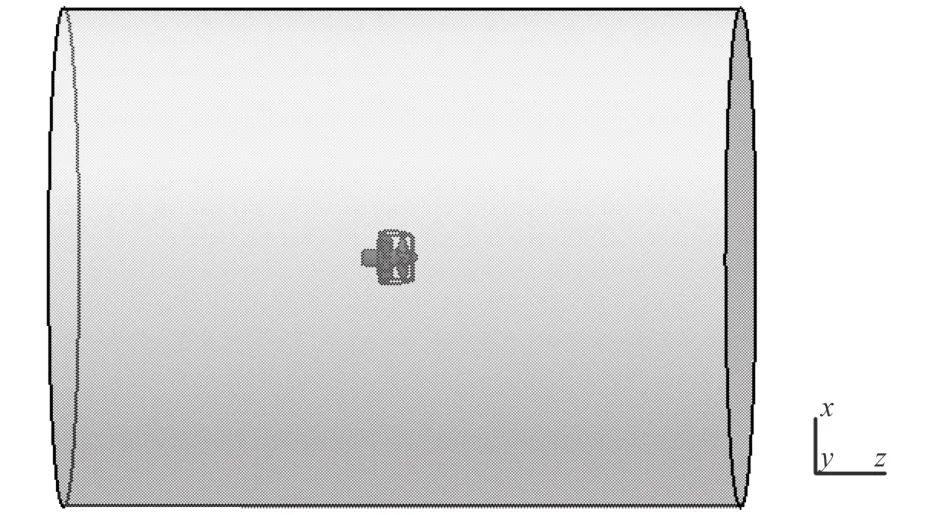
圖1　計算模型及坐標系Fig.1　Computational model and coordinate system

整個計算域分為轉子域及定子域。整個計算域采用了非結構化網格。轉子域與定子域通過 interface 面連接。為了控制轉子域附近的網格尺寸，采用 Gambit中的“尺度函數”對轉子葉片表面進行加密，尤其是對葉片梢部及導邊進行了加密。

1.2計算方法與邊界條件

泵噴推進器在艇后非均勻流場中以一定的轉速繞軸旋轉，屬于非定常流動問題。推進器性能分析可采用的數值計算方法有相對參考坐標系、動網格及滑移網格法。相對坐標參考系只適用于推進器的定常流動模擬；動網格方法可進行推進器的非定常數值計算，但在計算過程中需要對網格進行重構，較容易在計算中出現負體積，對網格質量要求高，計算量大，對計算機硬件的要求也更高，所以目前較少使用；目前比較常采用滑移網格方法模擬推進器的非定常性能。

基于 SST k-ω 湍流模型，本文首先采用相對參考坐標系法對泵噴推進器的定常性能進行數值計算，待定常計算充分收斂后且計算精度較高的情況下，以定常計算結果作為初始條件采用滑移網格方法對其非定常性能進行數值分析。計算時的邊界條件為：入口采用速度入口，給定來流速度，本文僅研究均勻來流下的非定常性能。出口采用為壓力出口。對流項離散格式為二階迎風格式，耗散項離散格式為二階中心差分格式。非定常計算中時間離散格式選用二階隱式格式。為保證殘差收斂精度達到 10-4，提高計算精度，壓力松弛因子取為 0.15，動量矩松弛因子 0.3，其余采用默認設置。

非定常計算時的時間步長 t 按照每個時間步內推進器旋轉 2° 進行設置，即n為推進器轉速（r/s）。

1.3數據處理

對導管式推進器進行定常與非定常計算穩定后，可根據式（1）～式（3）得到表征推進器性能的無因次系數，即推力系數與轉矩系數

式中：T和 Q為推進器推力與扭矩；J為進速系數；υ為入口速度；n和 D為推進器轉速與轉子直徑；ρ為水的密度。

在采用 Fluent 對推進器進行非定常計算中，將推進器產生的推力按照每個時間步長 t 保存 1次，得到推力值隨時間變化的時域圖。然后對其進行傅里葉變換可得到推力值在葉頻處的脈動力再根據式（4）可得到一階葉頻非定常力下的線譜噪聲級

由式（4）可知，為保證線譜噪聲預報達到 1dB的水平，非定常力的數值預報誤差不能大于 12％。

2　非定常計算結果分析

2.1計算方法驗證

采用相對參考坐標系方法與滑移網格方法分別對導管式推進器在進速系數分別為 0.6，0.8，1.0 下進行定常與非定常的計算。定常計算結果如表1所示，試驗數據來自于參考文獻［7］。進速系數為 0.6 與 0.8 時，數值計算誤差均在 5％以下；進速系數為 1.0 時，計算誤差有所增加，最大為 6.27％。

以定常計算結果為初始條件對 J=0.6 下導管式推進器采用滑移網格方法進行非定常計算，取時域上的平均值計算與結果如表2所示。非定常計算結果與試驗值相比，推力系數與扭矩系數誤差均在 10％以下，與定常計算結果相比，推力系數計算精度稍低，但精度已能滿足要求，扭矩系數精度得到提高。

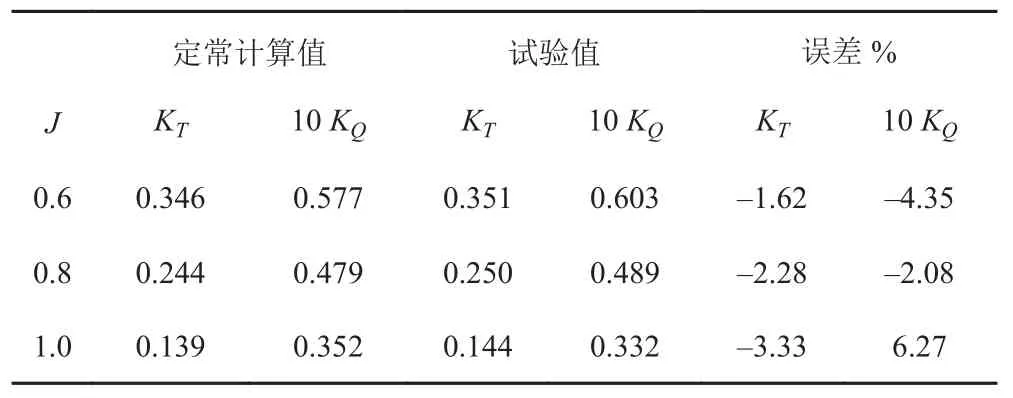
表1　定常計算結果Tab.1 Steady numerical results

表2　非定常計算結果Tab.2 Unsteady numerical results

2.2計算網格影響與結果分析

在研究推進器非定常性能時需要對推進器全流道進行數值計算，當轉子流道內的網格采用整體劃分時，各流道之間的網格無法保證完全一致，各個葉片受力受葉片網格的不均勻性的影響。非定常計算需要同時捕捉推進器總力和微小的脈動值。由于各個葉片受力不同，可能對推進器的總力影響不大，但是會影響非定常力的脈動值。為保證轉子各流道之間的網格是完全一致的，采用周期性的網格進行非定常分析，即首先生成轉子單流道的計算域網格，再將單流道網格旋轉復制得到全流道的計算網格。

為研究各流道網格不均勻性對非定常力的影響，分別對推進器在整體網格與周期性網格下的非定常性能進行數值分析，2 套網格保證網格尺度一致，消除網格尺度對計算結果的影響。

2.2.1計算網格對推進器性能的影響

圖2與圖3分別為 2 套網格下在 J=0.6 時非定常計算推力系數及扭矩系數的時域圖。由結果可知，2套網格下非定常計算時推力系數與扭矩系數隨時間變化的規律一致，計算到達穩定的時間基本一致，主要差別在數值大小上。

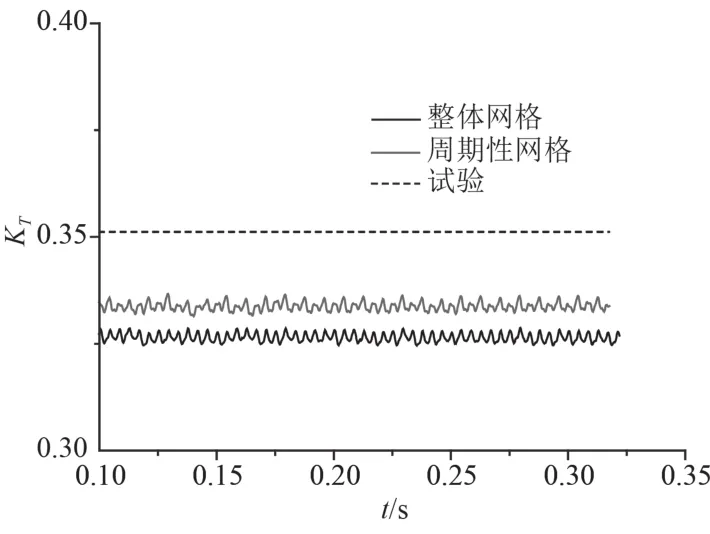
圖2　兩套網格下的推力系數 KT 時域圖（J=0.6）Fig.2　The time domain distribution of thrust coefficient （KT）under two sets of meshes （J=0.6）

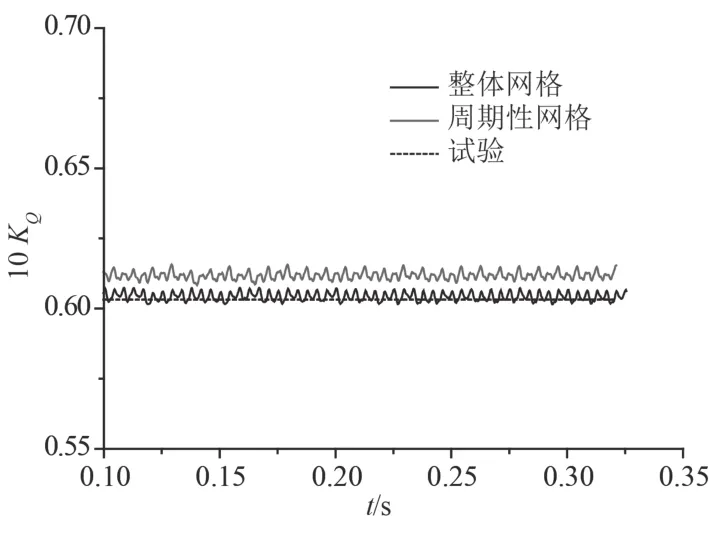
圖3　兩套網格下的扭矩系數 10 KO 時域圖（J=0.6）Fig.3　The time domain distribution of torque coefficient （10 KO）under two sets of meshes （J=0.6）

表3為周期網格下非定常計算后推力系數與扭矩系數值。與表1和表2中的數據相比，周期性網格下定常計算推力系數與扭矩系數計算精度有所降低，然而周期性網格下非定常計算推力系數誤差為 4.95％，推力系數計算精度得到提高，誤差較小。2 套網格下定常計算時扭矩計算精度比推力計算精度低，但非定常計算下扭矩計算精度得到大幅提高，推力計算精度降低，使得扭矩計算精度比推力計算精度高。

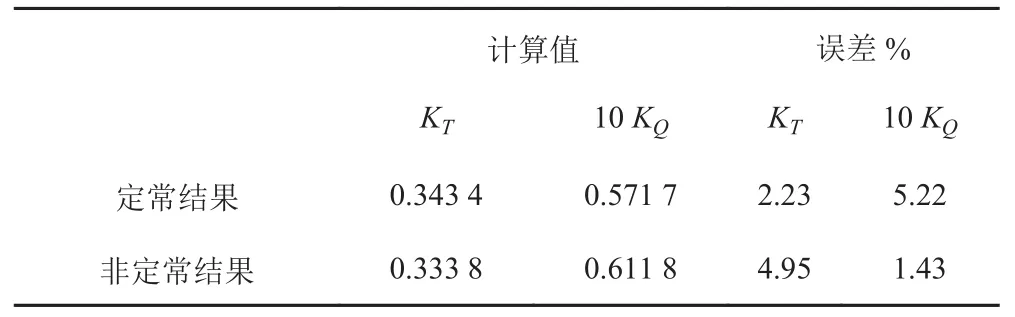
表3　周期性網格下的計算結果（J=0.6）Tab.3 Numerical results under periodic mesh （J=0.6）

2.2.2計算網格對非定常力的影響

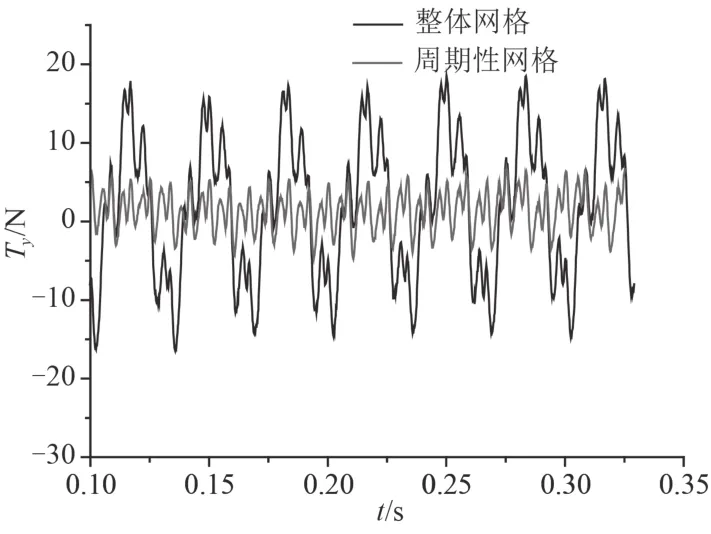
圖5　兩套網格下徑向力 Tv的時域分布圖Fig.5　The time domain distribution of radial force Tvunder two sets of meshes

由表4可知，整體網格下軸向平均脈動力為 4.23 N，周期性網格下的軸向平均脈動力為 4.218 N，2 套網格下的脈動強度基本一致。

表4　兩套網格下 x、y 及 z 方向上前3階葉頻處的非定常力Tab.4 The unsteady force at the first three order blade frequency in x，y，z direction under two sets of meshes

整體網格下 x 方向上的平均脈動力為 3.549 N，y方向上的平均脈動力為 5.249 N；周期性網格下 x 方向上的平均脈動力為 2.07 N，y 方向上的平均脈動力為2.974 N。與周期性網格相比，整體網格下 x 方向與 y方向上的脈動較為劇烈，這即是由于整體網格下各個葉片受力不一致導致額外增加了x 方向與 y 方向上的脈動值。

3　結 語

本文基于滑移網格方法對帶前置定子導管式推進器非定常性能數值計算方法進行了研究，主要研究了推進器在不同網格劃分方式下的非定常性能。可得到以下結論：

1）與定常計算結果相比，非定常計算下推進器的推力系數計算精度較低，但是能滿足要求；

2）與整體網格相比，周期性網格下非定常計算后推力系數計算精度得到提高；

3）與整體網格相比，周期性網格下非定常軸向脈動力基本相同，x 方向與 y 方向上的非定常脈動力明顯降低。

［1］潘光，胡斌，王鵬，等.泵噴推進器定常水動力性能數值模擬［J］.上海交通大學學報，2013，47（6）：932-937.

［2］譚廷壽，賀偉.螺旋槳非定常軸承力計算［J］.船海工程，2006，35（2）：42-46.

［3］熊鷹.非均勻流中螺旋槳空泡及脈動壓力的數值和試驗研究［D］.武漢：武漢理工大學，2002.

［4］胡小菲，黃振宇，洪方文.螺旋槳非定常力的黏性數值分析［J］.水動力學研究與進展，2009，24（6）：734-739.

［5］沈海龍，蘇玉民.船體黏性非均勻伴流場中螺旋槳非定常水動力性能預報研究［J］.水動力學研究與進展，2009，24（2）：232-241.

［6］姚震球，高慧，楊春蕾.基于滑移網格的帶螺旋槳艇體尾流場數值分析方法［J］.江蘇科技大學學報（自然科學版），2008，22（2）：15-20.

［7］HUGES M J，KINNAS S A.An analysis method for a ducted propeller with pre-swirl stator blades［C］//Proceedings of propeller/shafting's 91 symposium Virginia beach.Virgina，USA：SNAME，1991.

Research on numerical method of the unsteady performance of ducted propulsor

SHU Li-wei
（Navy Equipment Department，Beijing 100841，China）

Based on the sliding mesh method，the SST k-ω turbulent model was adopted to study the influence of different grid generation method on the unsteady performance of ducted propulsor with pre-stator.Firstly，based on the moving reference frame method and the sliding mesh method，the steady and unsteady performance was separately simulated.Then its numerical results were verified by comparing with experimental results.Furthermore，based on the mentioned method，the difference between the model in integral mesh and that in periodic mesh was compared，such as thrust coefficient，torque coefficient and unsteady force in x，y，z direction.The result provides a reference for further unsteady performance study of propulsor.

moving mesh；propulsor；periodic mesh；unsteady force

U664.3

A

1672-7619（2016）07-0026-04

10.3404/j.issn.1672-7619.2016.07.006

2016-04-20

舒禮偉（ 1978-），男，工程師，主要從事船舶結構設計工作。