基于有限元分析的滾齒SLD構建

李國龍　趙　君　劉小旭　楊　勇

1.重慶大學機械傳動國家重點實驗室，重慶，4000302.重慶機床(集團)有限責任公司，重慶，400055

?

基于有限元分析的滾齒SLD構建

李國龍1趙君1劉小旭1楊勇2

1.重慶大學機械傳動國家重點實驗室，重慶，4000302.重慶機床(集團)有限責任公司，重慶，400055

針對穩定性耳垂線圖(SLD)應用于滾齒顫振預測時存在動力學參數獲取困難、切削深度難以確定等問題，建立了考慮滾刀刀桿柔性的三維滾齒系統動力學模型，通過滾刀極限切屑厚度與軸向進給量的關系計算滾齒系統動力學參數，并在此基礎上繪制出滾齒SLD。設計了滾齒顫振實驗方案，通過采集的實驗數據分析平穩切削與顫振切削振動的特征量，確定顫振頻率及顫振主體，證實了所建立的動力學模型及SLD的有效性。所提方法為滾齒工藝顫振預測、切削參數選取提供了一種新手段。

滾齒；顫振；穩定性耳垂線圖；有限元分析

0　引言

在滾齒過程中，當系統結構參數或切削參數選用不當時，刀具與工件之間會產生強烈的自激振動，即產生滾齒“顫振”。顫振使滾齒過程不穩定、齒面質量和金屬切除率下降，嚴重時甚至會破壞滾刀和滾齒機，是制約滾齒機加工能力的一個主要因素[1]。抑制顫振的可行途徑是通過改變系統的結構參數或預測顫振發生的臨界條件[2-4]。顫振臨界條件的預測主要有三種方法：穩定性耳垂線圖(stability lobe diagram,SLD)、Nyquist曲線和有限元分析。其中，SLD可簡單而清晰地描述切削穩態與非穩態隨切削深度與速度變化的過程，進而預測系統的穩定性，并有助于切削速度和深度的合理選取，因而在切削顫振分析中得到廣泛應用[5]。

目前，SLD主要應用于理論切削深度恒定的車削工藝中，用于滾齒工藝時遇到兩個難點：①滾齒由一系列展成運動構成，不是單純的正交切削即進給方向始終垂直于工件表面，而滾削過程中的切削方向隨著刀刃切入切出而不斷變化，因而滾齒SLD中的極限切削寬度不再表現為徑向吃刀量沿刃傾角的分量；②SLD所需的動力學參數一般通過實驗獲取，而滾齒中獲取動力學參數尤其是動態切削力系數的相關實驗非常困難，若采用動態實驗并輔以數據處理，則結果誤差較大。

本文提出基于有限元法進行滾削工藝的三維動力學仿真，將滾齒加工的頂刃最大切屑厚度與SLD中的極限切削寬度聯系起來，并利用模態分析確定SLD所需的動力學參數，以構建符合滾齒實際工況的SLD。本文方法能使簡單清晰的SLD應用于復雜滾齒工藝中，為滾齒工藝顫振預測、切削參數選取提供參考。

1　滾齒加工的仿真前處理及結果

1.1滾齒加工的結構參數選取

滾齒系統穩定性因素分為兩類[6]：①工藝系統固有特性，包括滾齒機、滾刀、齒輪、夾具的結構形式、齒輪夾具的定位及固定方式等；②滾削工藝參數。

選取的滾齒系統結構參數如下：直齒圓柱齒輪模數m=6.5 mm，齒數Z=20，分度圓壓力角α=20°；A級阿基米德滾刀外徑de=110 mm，孔徑d=32 mm，全長L=100 mm，容屑槽數Zg=9。滾刀主要結構參數如圖1所示。

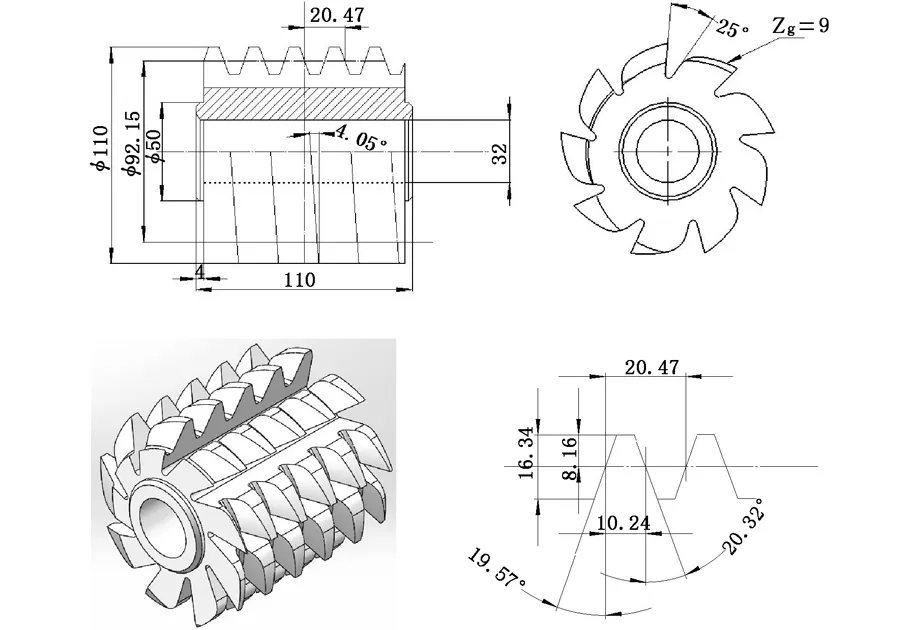
圖1　滾刀結構參數及其三維模型

滾刀以螺旋升角安裝在刀架軸上，滾齒仿真時將其視為剛體，則加工振動最終反映在刀架軸上。另外，因齒輪軸剛度遠大于刀架軸剛度，齒輪安裝部分也可視為剛體。故本文主要討論刀架軸結構參數對振動的影響。

由于顫振頻率總是接近于系統薄弱環節的某階模態固有頻率[7]，滾刀部件為滾齒系統的薄弱環節，故滾齒顫振將出現在刀架軸的某階固有頻率上，對刀架軸結構參數進行優化，可有效提高滾齒系統的抗顫振能力[8-9]。

1.2滾齒加工仿真模型的建立

選用ABAQUS/Explicit有限元軟件，在不考慮熱變形的前提下，將滾刀簡化為剛體、刀架軸簡化為簡支梁，得到滾齒簡化模型，如圖2所示。

圖2　滾齒模型

首先，確立材料模型。采用Jonhson-Cook強度模型，其應力與應變、應變率及溫度的關系為

(1)

式(1)等號右邊第一個圓括號代表材料彈塑性行為，第一個中括號代表材料黏性，第二個中括號代表材料的熱軟化效應。A、B、n為材料應變強化項系數，C為材料應變速率強化項系數，m為材料熱軟化系數。A、B、C、m、n通過實驗測得。

針對切屑斷裂失效，采用ABAQUS/Explicit的剪切失效準則與Jonhson-Cook斷裂準則設置參數。Jonhson-Cook斷裂準則本構方程為

(2)

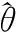
材料AISI4340的性能參數見表1，材料失效參數見表2。

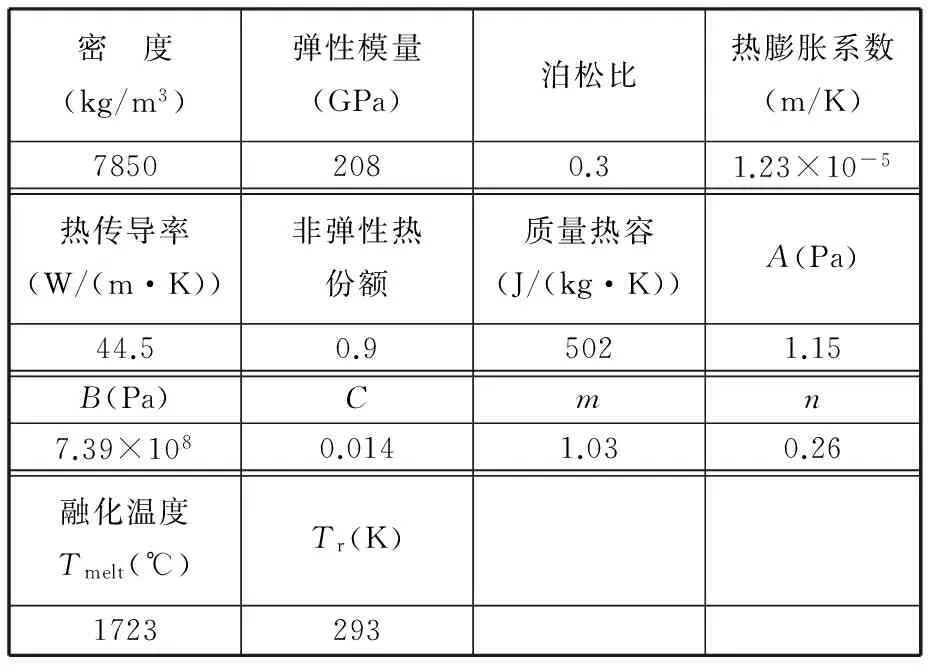
表1　AISI4340材料性能參數

表2　AISI4340材料失效參數

1.3滾齒加工參數的確定

滾齒切削運動較為復雜，既有滾刀轉動與齒坯轉動構成展成運動，又有滾刀沿齒坯軸線的進給運動以及由此產生的齒坯附加轉動。滾齒切削寬度主要表現為展成過程中滾刀頂刃能夠切削的最大切屑厚度h1max，如圖3所示。

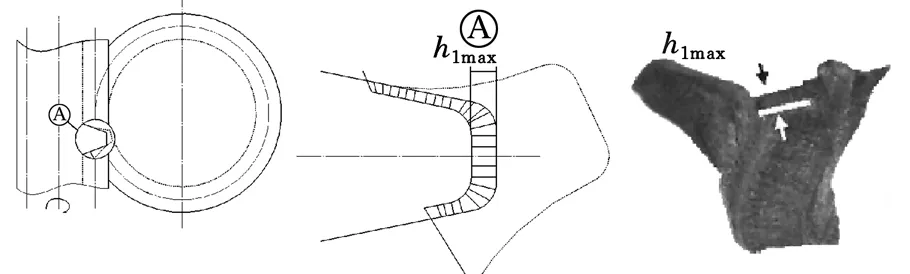
圖3　頂刃最大切削厚度h1max

采用Hoffmeister建立的滾齒頂刃切屑厚度與工件軸向進給量的關系式[10-14]：

fa=Fh1FmFZ2FdFN/Z0Fa

(3)

其中,Fh1、Fm、Fz2、Fd、FN/z0、Fa為6個影響因子，其計算式見表3。表3中，h1max為滾刀頂刃的最大切屑厚度，mm；fa為滾刀軸向進給量，mm/r ；β為齒輪分圓螺旋角，rad。

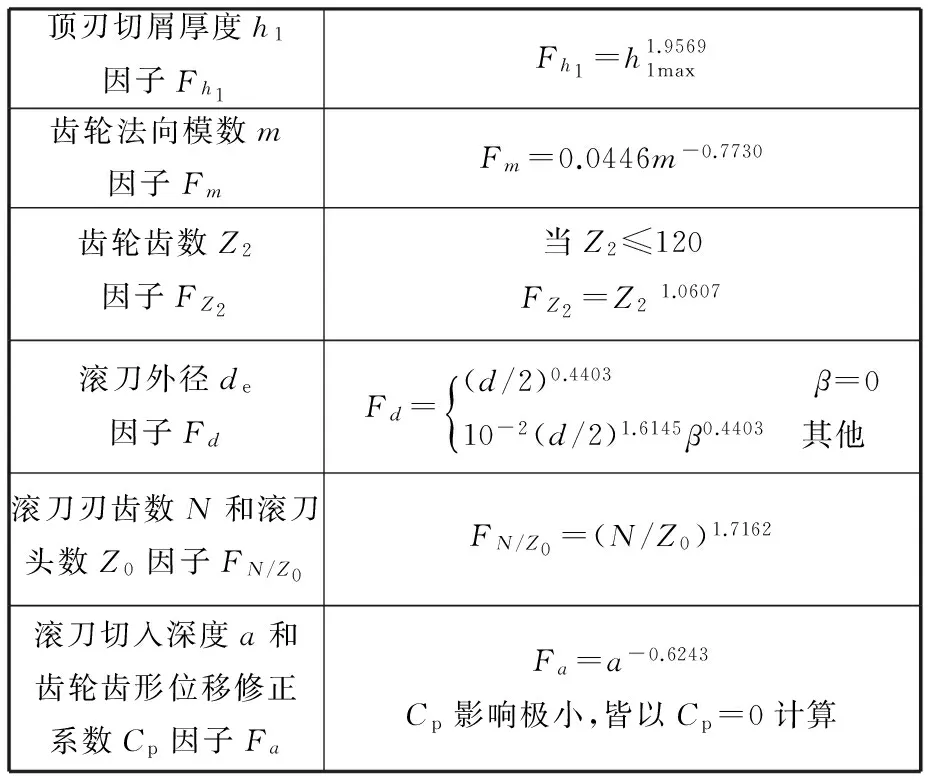
表3　fa各影響因子計算公式

滾削加工一般作為剃前或磨前工藝，滾刀切入深度即吃刀量取a=2.25mn。根據式(3)，在已知滾刀結構參數與齒輪參數的前提下，通過選取不同的軸向進給量，計算出對應的頂刃最大切屑厚度h1max，可為仿真與實驗參數選取提供依據。

1.4滾齒加工的動力學仿真

滾齒加工的起始位置，即切入開始時滾刀中心線距齒坯端面的距離t0的計算式如下：

(4)

h1=h-de(1-cosθ)/2

(5)

(6)

式中，h為齒輪全齒高；CZ為滾刀與齒輪的中心距；φ為滾刀分度圓螺旋升角。

從被加工齒輪的強度和齒輪滾刀材料的性能出發，滾刀切削時頂刃存在一個最大許可負荷，而負荷與切削量有著直接的關系，滾刀頂刃應規定一個最大許可切屑厚度。本文規定滾刀材料為高速鋼，故綜合考慮滾刀的硬質合金材料及齒坯材料,h1max選用國際標準推薦值0.49 mm，由式(3)得到相應軸向進給量fa為3 mm/r，對應的滾刀轉速為214 r/min，時間長度選取1 s，采用上述參數進行動力學仿真，滾削位移分布如圖4所示。

圖4　滾削仿真位移分布圖

由于滾刀旋轉位移遠大于刀架軸的振動位移，故需單獨顯示刀架軸以分析其振動位移，圖5為刀架軸的振動位移圖。

圖5　刀架軸振動位移圖

當軸向進給量變化時，仿真所得到的刀架軸振動位移也會發生變化，圖6、圖7分別為軸向進給量為4 mm/r、3 mm/r時的振動位移圖。

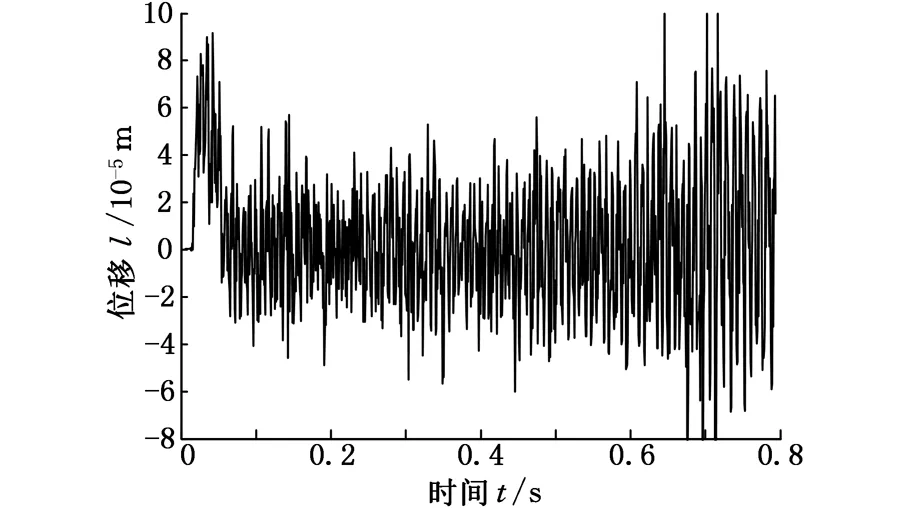
圖6　fa=4 mm/r時的振動位移

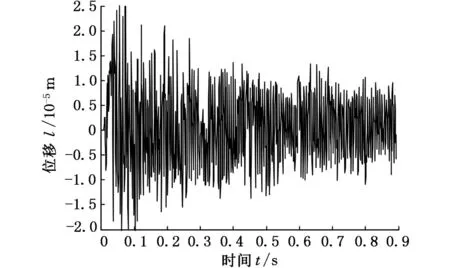
圖7　fa=3 mm/r時的振動位移

對比圖6、圖7，發現加大軸向進給量將導致顫振發生，軸向進給量變化引起滾刀頂刃切削厚度變化。通過快速傅里葉變換獲得滾齒系統共振頻率為760 Hz、顫振頻率為836 Hz，如圖8、圖9所示，印證了顫振頻率接近系統固有頻率這一說法。另外，在共振曲線的共振頻率f0峰值下3 dB處找到相應的f1和f2，用于求取阻尼比ξ，即

(7)

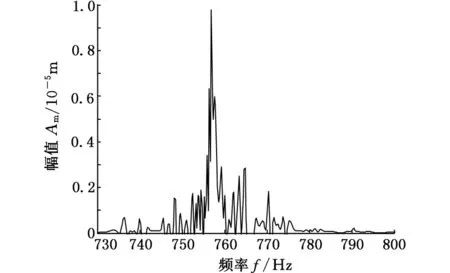
圖8　穩定切削頻域圖

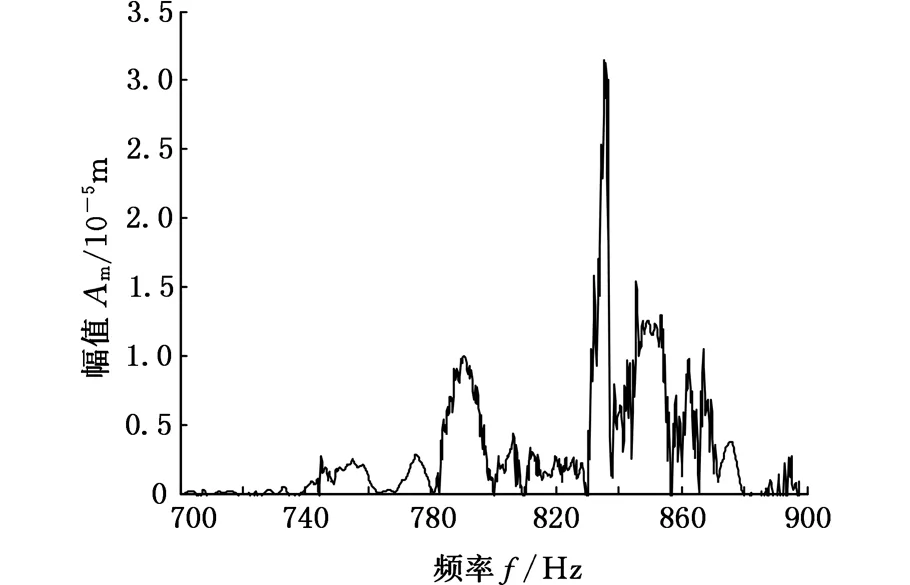
圖9　顫振發生時的頻域圖

2　SLD的構建

2.1SLD建模

滾齒加工的SLD是從二維平面角度構建，其動力學模型如圖10所示。

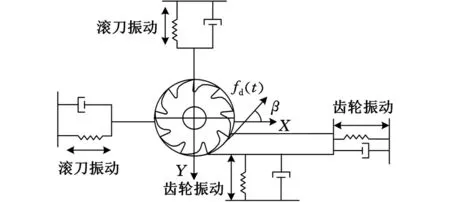
圖10　滾齒的二維動力學模型

滾齒顫振系統動力學模型的振動系統運動微分方程為

(8)

其中，fd(t)為動態切削力，me為振動系統等效質量，c為振動系統等效阻尼系數，k為振動系統等效剛度，β(齒輪分度圓螺旋角)為動態切削力與X坐標軸的夾角。X向的動態切削力為

Ff=kfb[x(t-TL)-x(t)]

(9)

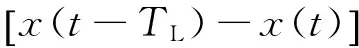
(10)

為簡化公式，設定參數之間的關系如下：

(11)

式中，ωn為系統固有頻率。

對式(10)進行拉普拉斯變換，得

(12)

由式(12)得到系統傳遞函數：

(13)

s=σ+jω

當σ=0時，系統處于臨界狀態，即系統極限切削寬度位置。其中，ω為系統的顫振頻率，其值略高于ωn。

將s=jω代入式(12)，得到傳遞函數的實部G(ω)與虛部H(ω)：

由于復振動信號中只有其實部才能真實描述振動信號的物理特征，故可得復振動信號臨界狀態下限切削寬度blim(與極限切削寬度等價):

令ω/ωn=λ，則有

(14)

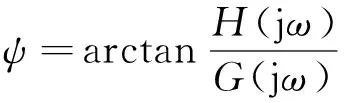
式中，n1為自然數，n1=0,1,2,…。

主軸轉速為

(15)

由式(13)、式(14)可知，在已知系統的動力學參數me、c、k、kf、ξ、ωn的條件下，blim與N是λ的函數。

2.2SLD參數的確定

首先，通過有限元靜力分析得到刀架軸連接點剛度(振動系統方程的等效剛度)kh=209.8MN/m。滾齒強迫再生顫振發生時，因顫振為滾齒誤差的主要來源，故可將滾刀部件的固有頻率作為滾齒系統的固有頻率。

基于ABAQUS進行模態分析[15]，提取滾刀系統的前6階特征值以及相關參數，見表4。其中TOTALMASSOFMODEL(模型可運動質量)值為9.857 152。

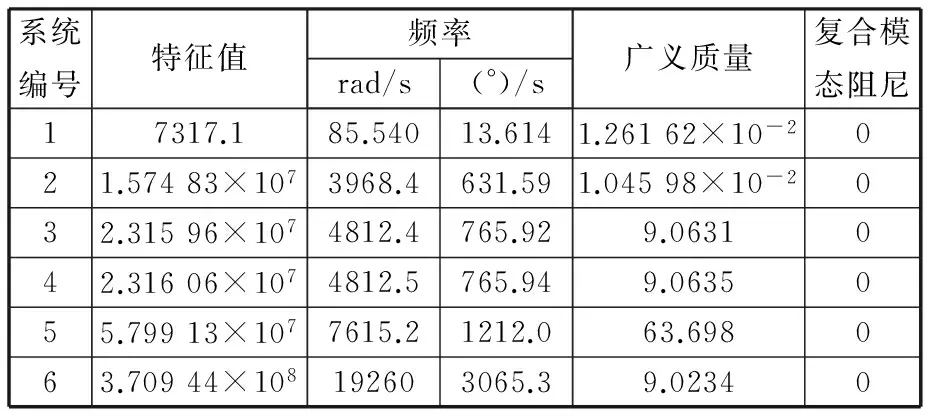
表4　滾刀系統振動參數

根據分析得到的各階模態參與系數，第4階振型主要在X方向上作用，且X向的總有效質量超過模型可運動質量的90%，模態提取合理。由表4可得ωn=4812.5，系統等效質量為數據中的廣義質量，me=9.0635。

在確定等效阻尼c時，采用Rayleigh阻尼進行瞬態動力學分析，公式如下：

C=α1M+β1K

(16)

其中，阻尼矩陣參數C是質量矩陣M和剛度矩陣K的線性組合，參數α1主要對低階頻響發揮作用，參數β1主要對高階頻響發揮作用，而顫振主要發生在低階頻響段，故只考慮參數α1。

取阻尼比ξ=0.038，通過式(10)求得系統等效阻尼c=3314.98，系統等效剛度k=209.8 MN/m。動態切削力系數kf表現為機床結構的動柔度和切削過程的動態特性。滾削力的變化由參與滾削的滾刀齒的切削量共同決定，通過滾齒動力學仿真得到0.2 s時的滾削力變化曲線，如圖11所示。

在三維CAD軟件SolidWorks中，通過布爾運算求得0.2s時總切屑量為2.362mm3，計算每個波峰波谷對應的動態切削力變化量，加權平均并除以總切屑量，得到kf=2.624×1010。使用MATLAB軟件繪制出SLD，如圖12所示。

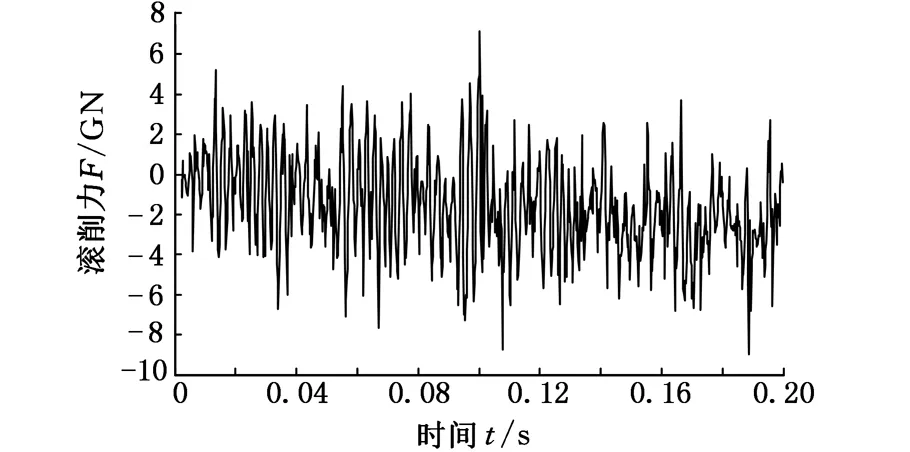
圖11　滾削力變化曲線

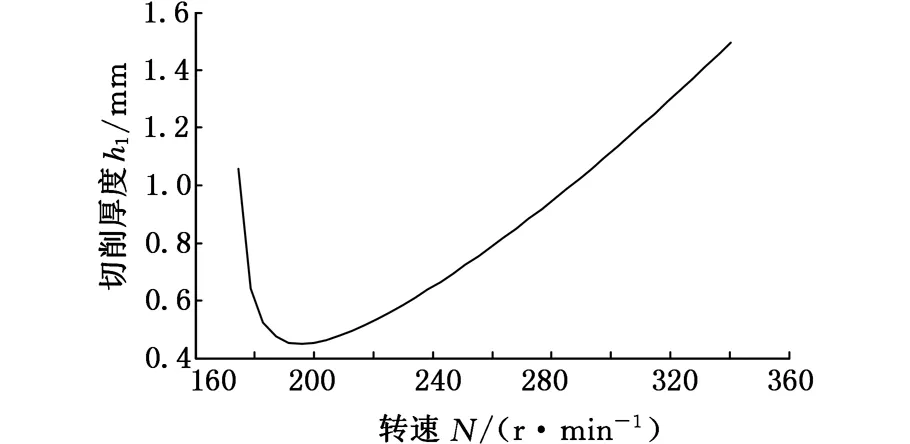
圖12　滾刀轉速214 r/min附近的SLD

在圖12中選取轉速214r/min附近的6個點進行仿真分析，得到表5所示的極限切厚。當滾刀轉速為214r/min時，其極限切厚為0.5mm，略大于推薦值h1max=0.49mm。因此，基于有限元仿真求取滾齒動力學參數進而構建SLD具有可行性。

表5　 SLD上6點對應的極限切屑厚度

3　SLD的實驗驗證

3.1實驗方案

在齒坯及滾刀結構參數給定且轉速保持不變的情況下逐步加大軸向進給量fa，若工件表面有清晰振痕且產生強烈噪聲時，認為系統發生了顫振。由時域信號分析及傅里葉變換可以看到，顫振時的振動信號幅值明顯大于正常切削狀態時振動信號的幅值，顫振頻率出現在切削系統某階固有頻率附近，并且顫振能量集中在很窄的范圍內。

如圖13所示，通過傳感器信號采集，并進行數據處理，將發生顫振的軸向進給量轉換為最大切屑厚度h1max記錄下來。

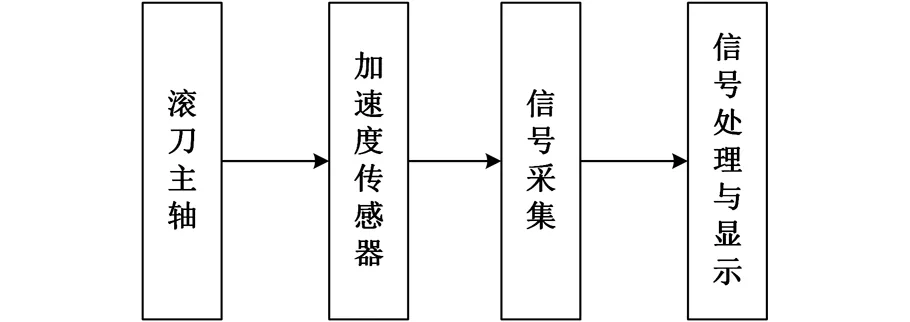
圖13　實驗方案

如表6所示，改變軸向進給量，重復以上步驟。

表6　主軸轉速對應的不同軸向進給量

3.2實驗器材及布置

利用加速度傳感器測量滾刀與齒輪軸X向上的振動加速度，并通過二次積分來反映滾齒系統的振動位移變化情況，實驗器材見表7。

表7　滾齒顫振實驗器材

因滾刀及齒輪均要旋轉，故將帶磁座加速度傳感器分別布置在刀架軸的防護罩殼和齒輪軸的頂尖導軌上，如圖14所示。信號在線測量界面如圖15所示。

圖14　加速度傳感器現場安裝位置

圖15　信號在線測量界面

3.3實驗結果

3.3.1 空轉

將滾刀調整到切削位置，主軸轉速調整到200 r/min，滾齒機空轉加工，提取滾齒機穩定運行時滾刀軸與齒輪軸在X方向上的自功率譜曲線，如圖16、圖17所示。空轉時，滾刀軸X方向在338 Hz處振幅取得最大值0.142 m/s2，齒輪軸X方向在500 Hz處振幅取得最大值0.128 m/s2。

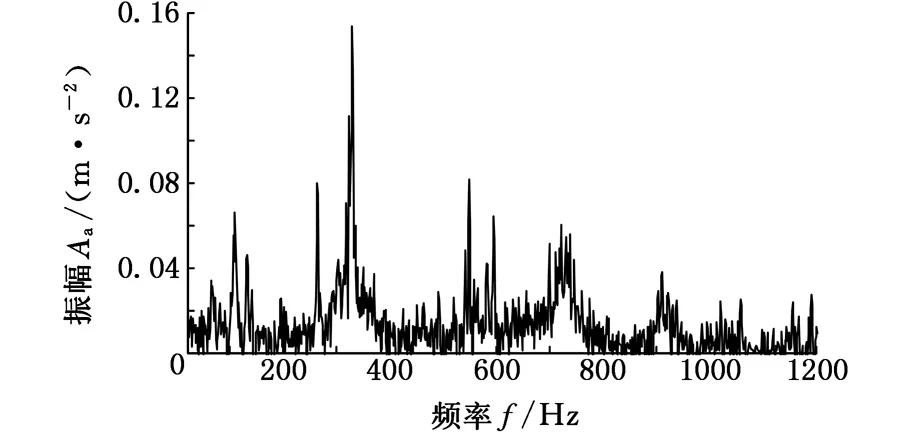
圖16　空轉時滾刀軸X方向自譜曲線

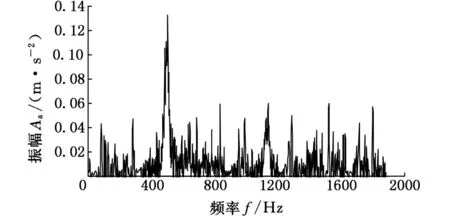
圖17　空轉時齒輪軸X方向自譜曲線

3.3.2平穩切削(軸向進給量為2.7 mm/r)

由圖18、圖19可知，滾刀軸在830 Hz附近振幅略有增加，其他處變化不大，X方向在898 Hz處最大振幅為0.28 m/s2；齒輪軸X向的峰值主要發生在492 Hz和1200 Hz附近，其大小為0.14 m/s2。另外，平穩切削與空轉振動幅值接近。

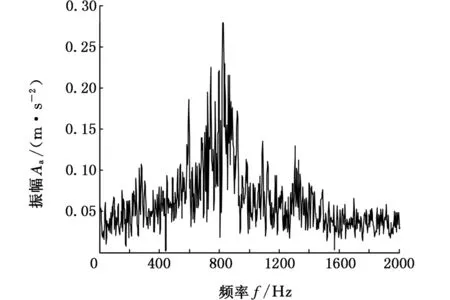
圖18　平穩切削時滾刀軸X方向自譜曲線

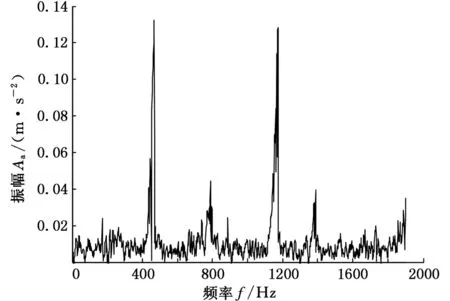
圖19　平穩切削時齒輪軸X方向自譜曲線

3.3.3顫振切削

逐漸加大軸向進給量，當軸向進給量達到2.9 mm/r時，系統發生顫振，如圖20所示。

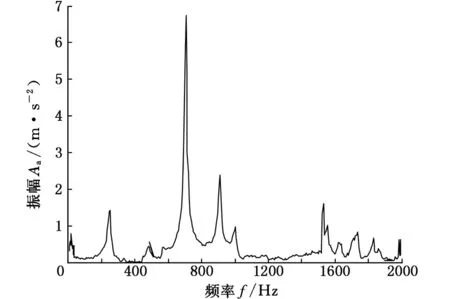
圖20　顫振發生時滾刀軸X方向自譜曲線

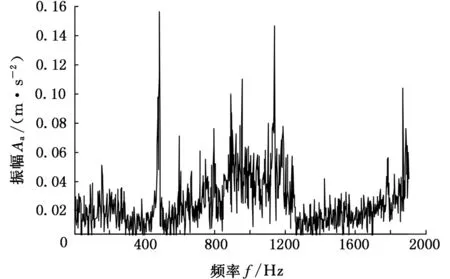
圖21　顫振發生時齒輪軸X方向自譜曲線

由圖20可知，當軸向進給量至2.9 mm/r時，刀架軸在850 Hz附近發生顫振，其X方向的最大振幅為7 m/s2，其他處變化不大。由圖21可知，齒輪軸仍在492 Hz和1200 Hz附近振幅達到X向最大值，其值0.19 m/s2也與平穩切削時的振幅接近。

平穩切削(軸向進給量為2.7 mm/r)時，切削過程平穩、無刺耳噪聲、工件表面光滑、無振紋，如圖22所示。繼續加大軸向進給量，當進給量達到2.9 mm/r時，振幅在顫振頻率范圍內明顯增大，且噪聲刺耳、齒面出現魚鱗狀振紋，此時系統發生顫振，如圖23所示。

圖22　平穩切削齒面　圖23　顫振切削齒面

通過實驗發現：顫振發生時，滾刀轉速為200 r/min，軸向進給量所對應的頂刃切屑厚度按式(2)計算為0.488 mm，處于所構建的SLD曲線附近；滾齒系統的顫振頻率在830～850 Hz之間，與滾刀部件的固有頻率接近，顫振優先發生于滾刀部件。實驗得到的穩定切削深度點與基于仿真方法繪制的SLD得到的相關數據點基本一致，驗證了通過仿真方法獲得SLD的正確性。

4　結論

(1)本文通過選擇合適的材料、本構模型與切屑斷裂準則與失效準則，建立了圓柱直齒輪滾削的有限元模型，在此基礎上，構建了能夠反映不同軸向進給量與滾削速度下預測滾齒加工穩定性的動力學模型。

(2)通過滾齒有限元仿真得到相關動力學參數，并將滾齒極限切屑厚度與軸向進給量聯系起來，實現了SLD在滾削工藝中的應用。

(3)構建了顫振實驗方案，通過實驗驗證了動力學仿真結果與構建的SLD的正確性，得到該滾齒系統的顫振頻率范圍及顫振主體。

(4)本文方法對于預測滾削顫振、選取合適的切削參數，具有一定的參考價值。

[1]Huang Qiang，Zhang Genbao，Chen Kun. Continuity and Break of Chatter Vibration Status[J].Chinese Journal of Mechanical Engineering,2008,21(4):92-96.

[2]王躍輝,王民.金屬切削過程顫振控制技術的研究進展[J].機械工程學報,2010,46(7):166-174.

Wang Yuehui,Wang Min.Advances on Machining Chatter Suppression Research[J].Journal of Mechanical Engineering,2010,46(7):166-174.

[3]王民,費仁元.基于電流變材料的切削顫振在線監控技術研究[J].機械工程學報,2002,38(12):93-97.

Wang Min,Fei Renyuan.Research on Monitored Control of Machining Chatter Based on Electrorheological Fluids[J]. Journal of Mechanical Engin-eering,2002,38(12):93-97.

[4]Behnam M I, Yussefian N Z. Dynamic Simulation of Boring Process[J]. International Journal of Machine Tools and Manufacture,2009,49(14):1096-1103.

[5]Meritt H E.Theory of Self-excited Machine-tool Chatter[J].Transactions of the ASME Journal of Engineering for Industry,1965,87: 447-454.

[6]楊勇,王時龍,田志峰,等.大型數控滾齒機立柱動力學仿真分析[J].中國機械工程,2013,24(11):1473-1479.

Yang Yong,Wang Shilong,Tian Zhifeng,et al.Dynamics Simulation Analysis of Column for Large-scale NC Gear Hobbing Machines[J].China Mechanical Engineering, 2013,24(11):1473-1479.

[7]閻兵,張大衛,徐安平,等.球頭刀銑削過程動力學模型[J].機械工程學報,2002,38(5):22-26.

Yan Bing,Zhang Dawei,Xu Anping,et al.Dynamic Modeling of Ball End Milling[J].Journal of Mechanical Engineering,2002,38(5):22-26.

[8]劉潤愛,張根保,黃強,等.提高零傳動滾齒機系統剛度的研究[J].系統仿真學報,2006,18(3):710-712.

Liu Run’ai,Zhang Genbao,Huang Qiang,et al.Study on System Stiffness Enhancement of Zero-drive Gear Hobbing Machine[J].Journal of System Simulation,2006,18(3):710-712.

[9]吳化勇.高速切削系統動態特性研究[D].濟南：山東大學,2005.

[10]Sima M, Ozel T.Modified Material Constitutive Models for Serrated Chip Formation Simulations and Experimental Validation in Machining of Titanium Alloy Ti-6A-4V[J].International Journal of Machine Tools & Manufacture,2010,50(11):943-960.

[11]Oze T, Zeren E. Finite Element Method Simula-tion of Machining of AISI 1045 Steel with a Round Edge Cutting Tool[C]//Proceedings of 8th CIRP International Workshop on Modelling of Machining Operations. Chemnitz,2005:533-541.

[12]Altintas Y.Manufacturing Automation[M].Cambridge： Cambridge University Press,2000.

[13]Mahnama M, Movahhedy M. Application of FEM Simulation of Chip Formation to Stability Analysis in Orthogonal Cutting Process[J].Journal of Manufacturing Processes,2012,14(3):188-194.

[14]朱育權,千學明,林曉萍.1CL50型機床立柱振動模態分析[J].西安工業大學學報,2007,27(3):215-218.

Zhu Yuquan,Qian Xueming,Lin Xiaoping.Modal Analysis of a Column of 1CL50 Machine Tools[J].Journal of Xi’an Technological University,2007,27 (3):215-218.

[15]成群林,柯映林,董輝躍,等.高速硬加工中切屑成形的有限元模擬[J]浙江大學學報(工學版),2007,41(3):509-513.

Chen Qunlin,Ke Yinglin,Dong Huiyue, et al. Simulation of Chip Formation in High-speed Hard Machining[J].Journal of ZhejiangUniversity(Engineering Science), 2007,41(3):509-513.

(編輯陳勇)

作者簡介：李國龍，男，1969年生。重慶大學機械傳動國家重點實驗室教授、博士研究生導師。主要研究方向為精密制齒技術與裝備、智能數控技術等。獲省部級一等獎1項，發表論文40余篇。趙君，男，1991年生。重慶大學機械傳動國家重點實驗室碩士研究生。劉小旭，男，1988年生。重慶大學機械傳動國家重點實驗室碩士研究生。楊勇，男，1980年生。重慶機床(集團)有限責任公司檢測技術研究所所長、高級工程師、博士。

Construction of SLD in Gear Hobbing Process Based on FEA

Li Guolong1Zhao Jun1Liu Xiaoxu1Yang Yong2

1. The State Key Laboratory of Mechanical Transmissions, Chongqing University，Chongqing，400030 2. Chongqing Machine Tool(Group) Co., Ltd., Chongqing，400055

Aiming at the problems of predicting gear hobbing chatters by SLD where the dynamics parameters were hard to get and the cutting depth was hard to determine, a 3D gear hobbing system dynamics model was established considering cutters arbor flexibility of hob. Hobbing system dynamics parameters was calculated with the relationship between limit chip thickness of hob and axial feed. And the SLD of gear hobbing was drawn based on the model. A hobbing chatter experiment plan was designed, features of steady state cutting and chatter cutting was analyzed via experimental data collected, and chatter frequency and chatter subject was determined, the validity of dynamics model established and SLD was verified. It provides a new method to predict hobbing chatter and to choose cutting parameters.

hobbing; chatter; stability lobe diagram (SLD); finite element analysis(FEA)

2015-06-17

國家科技支撐計劃資助項目(2014BAF08B02)；重慶市科技人才培養計劃資助項目(cstc2013kjrc-qnrc70001)

TG156

10.3969/j.issn.1004-132X.2016.17.003

文澤軍，男，1966 年生。湖南科技大學機械設備健康維護湖南省重點實驗室教授、博士。主要研究方向為機電系統動力學與控制、制造系統質量控制、制造過程監測與控制和面向產品制造/裝配過程的穩健設計。劉湛，男，1990年生。湖南科技大學機電工程學院碩士研究生。金永平，男，1984 年生。中南大學機電工程學院博士研究生。田續玲，女，1975年生。湖南科技大學海洋礦產資源探采裝備技術湖南省工程實驗室助理研究員。黃良沛，男，1971年生。湖南科技大學機械設備健康維護湖南省重點實驗室教授。