基于漸進法的約束阻尼結構拓撲多目標動力學優化

賀紅林　陶　結　劉堯弟　凌　普

南昌航空大學， 南昌，330063

?

基于漸進法的約束阻尼結構拓撲多目標動力學優化

賀紅林陶結劉堯弟凌普

南昌航空大學， 南昌，330063

為實現阻尼結構減振優化,從阻尼材料的力學本構出發，基于虛功原理建立了約束阻尼板動力學平衡方程，從阻尼耗能角度推導出模態損耗因子解析計算式。構建了以模態損耗因子最大且模態頻率變動最小為目標、以阻尼材料用量為約束的阻尼板多目標優化數學模型。在對模態損耗因子及模態頻率靈敏度進行推導的基礎上，構建了歸一化復合靈敏度算式，并引入拓撲漸進法求解優化模型。編制出阻尼板漸近法優化程序，并對阻尼板進行了優化仿真。結果顯示，采用多目標拓撲漸進優化，既能大幅提高阻尼材料的減振效能，又能保證阻尼板頻率特性的穩定，且可較大幅度地降低阻尼材料用量。對阻尼板進行了諧響應分析，驗證了優化結果的有效性。該優化法在對結構動力學特性有嚴格要求的減振設計中存在應用前景。

約束阻尼結構；模態損耗因子；模態頻率；動力學優化

0　引言

工程結構在使用過程中常受到強烈的振動與沖擊，造成機械精度下降、振動疲勞等問題，因此有必要對振動進行有效控制。對結構振動進行控制的方法很多，而利用阻尼材料進行減振處理是減振降噪技術的主要措施之一[1]。附加阻尼結構根據耗能機理和特點不同可分為約束型阻尼結構和自由型阻尼結構。兩者均通過在表面敷設黏彈性阻尼材料以達到減振的目的，將阻尼材料完全敷設于結構表面，不僅增加經濟成本，也可能大幅改變結構動力學性能。因此，必須在盡可能少地使用阻尼材料前提下，使結構獲得最佳減振效果。從結構拓撲優化角度看，楊德慶等[2]提出了阻尼胞單元和阻尼拓撲敏度等概念，建立了基于阻尼拓撲敏度綜合評價的阻尼材料拓撲優化準則。張志飛等[3]基于密度法，建立了以模態阻尼比最大化為目標的優化數學模型。王明旭等[4]基于均勻化方法建立了以模態阻尼比最大化為目標函數的優化數學模型，通過數值方法得到阻尼材料最優分布構形。李攀等[5]基于SIMP插值模型和變密度方法，采用優化準則對阻尼材料進行了優化布局。李亞娟等[6]結合變密度法在正常環境下對板件進行了減振降噪拓撲優化設計。郭中澤等[7]采用變密度法對阻尼結構進行拓撲優化設計，得到阻尼材料最優分布構形。趙冬艷等[8]采用遺傳算法對約束阻尼梁進行減振優化。Zheng等[9]以能量最小化為優化目標，基于遺傳算法對阻尼材料優化布局進行研究。由此可見，阻尼結構優化方面已經取得不少成果，但變密度法和準則法等數學推導嚴格，算法復雜，實際應用較為困難。而Xie等[10]提出的結構漸進法則具有算法簡單、計算效率高的特點。已有的研究多針對單一目標展開優化，但在工程應用中，設計目標通常包含多方面因素，故推進多目標研究更有實際意義。實踐證明，約束型阻尼結構相對于自由阻尼結構耗能效率更高[1]，故本文采用漸進優化法，研究約束層阻尼板的多目標復合拓撲優化問題。

1　模態損耗因子建模

約束阻尼結構減振技術是通過提高結構的阻尼力實現的。考慮到模態損耗因子能較綜合地表征結構承受應變時以熱能方式耗散機械能的能力，為便于計算附加阻尼結構的耗能效率，有必要推導模態損耗因子的算式。當約束阻尼結構振動時，主要受阻尼力和慣性力等外力作用，對結構進行有限元網格化后，單元體隨結構一起振動。根據虛功原理，單元外力在虛位移上所做虛功等于其虛位移上的應變能[11]，故有

∫vσTδεdv=∫vFTδudv+Wm

(1)

式中，F為單元內任意點所受除阻尼力以外的外力矢量；σ為單元應力向量；δu為該點虛位移向量；δε為由δu引起的虛應變向量；Wm為阻尼力所作虛功；積分區域v表示單元所在區域。

式(1)為單元的功能平衡方程。當單元做自由振動時，外力F即慣性力，根據達朗貝爾原理，有

(2)

式中，ρ為單元的材料密度；u為單元內任意點位移向量；t為時間。

將式(2)代入式(1)，可得

(3)

根據有限元理論，單元i內任一點位移可由單元的結點位移經插值而得，即

u=Nui

(4)

式中，N為單元形函數矩陣，ui為單元節點位移列向量。

單元應變與位移間關系用幾何方程描述，即

ε=Bu

(5)

式中，ε為應變向量；B表示單元形函數矩陣。

單元應力與應變之間的關系可用物理方程描述，即

σ=Dε

(6)

式中，σ為應力向量；D為結構的彈性矩陣。

結合式(3)～式(6)，可得

(7)

(8)

其中，S=BN，δui為單元節點i的虛位移向量。設黏彈材料的阻尼力正比于應變速度，則阻尼應力為

(9)

式中，σz為阻尼應力矢量；β為比例系數。

故阻尼應力在虛應變上做的虛應變能：

(10)

將式(7)、式(8)、式(10)代入式(1)，則有單元的動力學平衡方程：

(11)

其中，mi、ci、ki分別為單元的質量矩陣、單元阻尼矩陣、單元剛度矩陣，且分別為

(12)

根據約束阻尼結構的結構組成，可將單元矩陣質量陣、阻尼陣、剛度陣進行組裝，從而建立結構整體的自由振動方程：

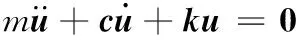
(13)

研究表明，工程結構特定階次模態的損耗因子可根據結構的耗能和動態應變能來求解[12]。考慮到在約束阻尼結構中，基層與約束層的阻尼耗能能力遠低于黏彈層，故其r階模態損耗因子可根據下式計算：

(14)

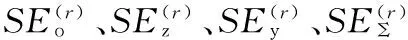
(15)

其中，ko、kz和ky分別為基層、阻尼層和約束層的剛度矩陣部分， 黏彈層的r階模態阻尼耗能為

(16)

式中，ηz為阻尼材料損耗因子。

將式(15)、式(16)代入式(14)，可得結構的r階模態阻尼損耗因子為

(17)

2　結構動力學優化建模

2.1優化數學模型

構建適當的優化模型是實現約束阻尼結構減振優化的前提，且關系到設計結果的好壞。振動位移、振動速度和振動加速度大小能直觀地表征結構振動效應的強弱，理論上應基于這些物理量進行結構優化，但考慮到優化實現時，不可能針對結構的所有點而只能擇取少數點的振動位移或速度進行優化計算，故所得優化結果將帶有很大的局限性。

眾所周知，約束阻尼結構通過黏彈性阻尼材料的剪切變形來最大限度地消耗結構的振動能量，結構的一定階次振動模態的阻尼損耗因子能綜合反映阻尼材料消耗結構整體的該階次振動動能的能力，為此，引入模態損耗因子作為評價結構黏彈阻尼材料優化布局的技術指標。在進行阻尼減振結構設計時，一般是先根據結構系統的功能，確定阻尼結構基層形狀與尺寸，再根據減振特性要求，規劃結構的阻尼材料布局。對于許多重要工程結構如航天器太陽能板等，在進行減振設計時，通常不允許結構頻率產生太大的變動，以保證結構系統最大程度地避開共振頻率，在此條件下，模態頻率變化也應成優化目標的一部分。結構的動力學優化通常受幾何條件、應力、位移等多因素限制，因此要對幾何邊界、尺寸做出限制以防止出現不合實際的邊界或尺寸，且應保證結構應力不能超過材料的許用應力值，且結構中的某些點或部分的位移也需控制在合理的范圍內。

基于以上考慮，為最大限度地消耗振動能量并盡量保證結構的原有頻率特性，以模態損耗因子最大、頻率變動最小為聯合目標，以阻尼單元的有或無為設計變量，以阻尼材料用量等為約束條件，建立了結構的拓撲優化數學模型：

(18)

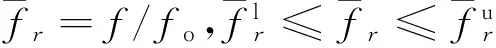
2.2模態損耗因子靈敏度

為了對式(18)進行求解，有必要推導出模態損耗因子對于拓撲設計變量的靈敏度顯式計算式，這是因為通過計算拓撲變量的靈敏度，可推斷結構動力學特性的變化趨勢，為結構優化迭代提供最適方向，有助于快速尋找到滿足約束條件的最優幾何拓撲。對于已進行有限元網格劃分的阻尼板，每個單元的幾何結構即是一個拓撲設計變量，當結構的各單元尺寸相等，刪除某阻尼單元時，將結構的模態損耗因子變化，其變化量即為該單元的目標函數靈敏度。當第i個阻尼單元及相應的約束層單元被刪除時，結構第r階模態損耗因子變化量為

(19)

考慮到采用漸進法對式(19)進行求解時，在每輪優化迭代中所刪單元數非常有限，因此結構的總體變化較小，故可近似地認為：

(20)

(21)

式(21)表示第i個阻尼單元刪除后，約束阻尼結構第r階模態損耗因子變化量。

2.3模態頻率靈敏度

影響結構系統頻率的因素較多，且其影響規律較為復雜。頻率靈敏度定義為結構的單位體積變化所引起的頻率變化。單元的頻率靈敏度作為結構系統頻率優化的依據，為優化提供迭代方向信息。根據結構振動理論， 得到阻尼板振動特征方程為

(22)

式中，λ(r)為結構特征值；ω(r)為結構圓頻率。

利用瑞利商進行計算，可得

λ(r)=k(r)/m(r)

(23)

其中，k(r)、m(r)為第r階模態剛度和模態質量，即

(24)

若刪除阻尼單元i，由刪除單元引起特征值變化量為

(25)

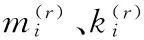
在優化迭代過程中，由于每次迭代刪除單元數量較小，可假設優化后，結構振型不變：

(26)

式中，kz,i、ky,i分別為在刪除第i個單元之前由阻尼層和約束層單元形成的總體剛度陣；mz,i、my,i分別為阻尼層和約束層單元形成的總體質量陣。

將式(26)代入式(25)，可得黏彈阻尼單元i的頻率靈敏度計算式：

(27)

式中，mi為刪除第i個單元前結構的總體質量矩陣。

3　漸進法優化模型求解

為求解式(18)，可建立待控結構，并將阻尼材料完全覆蓋于待控表面，此時的拓撲優化即依據漸進優化算法逐漸刪除低效黏彈阻尼單元。為實現式(18)的求解，基于ANSY的APDL語言編寫漸進優化算法；為使得約束阻尼材料布局邊界清晰，可制造性強，按照Sigmund等[13]提出的濾波方法編制獨立網格濾波程序，以改善阻尼材料優化后棋盤格、網格依賴性等問題。約束阻尼板進行拓撲優化，就是逐步刪除無效或低效單元，在減小阻尼材料用量的情況下，使得阻尼結構模態損耗因子最大化且模態頻率變動最小，因此，圖1的優化流程主要步驟有：

(1)建立約束阻尼結構有限元模型，設定邊界條件。

(2)模態分析并提取單元模態應變能和模態動能。

(3)分別按式(21)、式(27)進行損耗因子靈敏度和模態頻率分析，并選取合適的濾波半徑，對靈敏度濾波處理。由于損耗因子靈敏度值和頻率靈敏度值數量級不同，故對二者進行歸一化處理，并按式(18)進行加權，得到新的靈敏度集合。

(4)對靈敏度集合中靈敏度值進行排序，提取正靈敏度中最小值ξ1min和負靈敏度中最大值ξ2max。

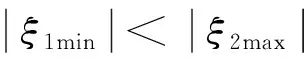
(6)若滿足材料用量要求，則優化結束；不滿足，則重復步驟(2)至(6)，直到滿足用量要求，優化結束。若僅針對單目標優化，則優化流程與多目標相同。

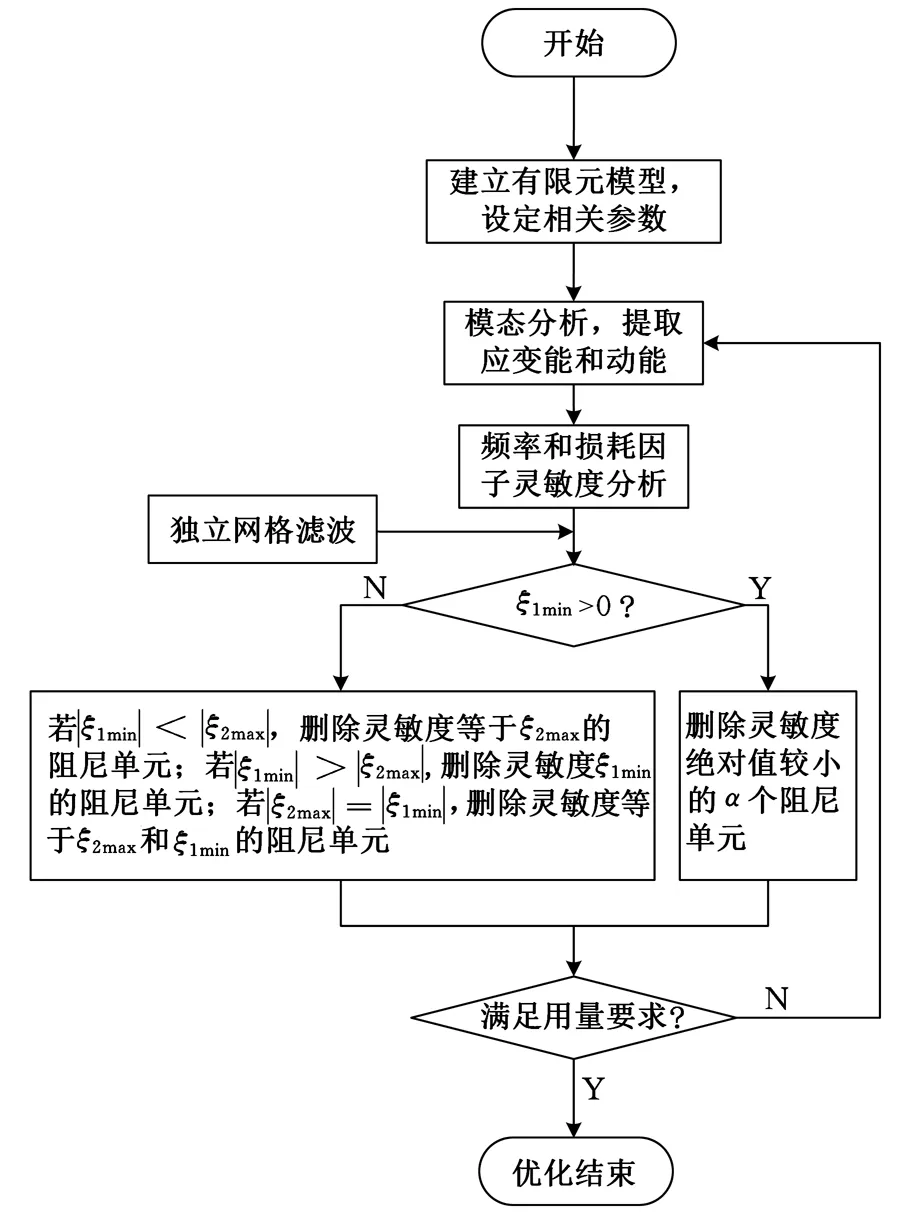
圖1　約束阻尼材料拓撲優化程序流程圖

4　優化算例

為充分驗證上述漸進優化算法的有效性，本文針對矩陣板進行漸進優化仿真，該板長0.84m，寬0.4m。基層彈性模量為70GPa，泊松比為0.3，密度為2800kg/m3，基層厚度為6.5mm。黏彈性層彈性模量為12MPa，泊松比為0.495，密度為1200kg/m3，阻尼損耗因子為0.5，黏彈性層厚3mm。約束層彈性模量為70GPa，泊松比為0.3，密度為2700kg/m3，約束層厚2mm。阻尼板邊界約束條件：矩形板四邊簡支。在對阻尼結構進行有限元網格劃分時，由于Solid185號單元能解算黏彈性大變形且可模擬彈性結構小變形，故黏彈性層采用Solid185號單元劃分網格，厚度方向劃分為兩層單元，每層單元數量為20×24。

圖2為阻尼結構有限元劃分模型和按單元編號刪除阻尼單元的非優化布局圖。圖3為目標階次模態振型及應變分布圖，圖中MX、MN表示阻尼板上模態應變最大和最小位置，用顏色變化表征應變值漸變。本文按阻尼材料刪除率為50%的要求進行材料優化布局。圖4所示為基于漸進優化算法，僅以損耗因子、模態頻率為優化目標和綜合考慮二者而獲得的阻尼材料最佳布局。在優化過程中，以特定的準則逐漸刪除處于無效或低效狀態的單元，從結構耗能的角度來說，黏彈阻尼材料模態應變能與其耗能能力呈正向關系，阻尼單元模態應變能小，則耗散能力較弱，將優先從材料布局中被刪除，故阻尼材料呈上述分布較為合理。從圖4還可看出，優化布局邊界清晰，獨立網格濾波技術很好地解決了優化過程中的棋盤格式和網格依賴性。

(a)網格劃分及約束　　(b)按單元編號刪除模式圖2　約束阻尼板未優化布局圖

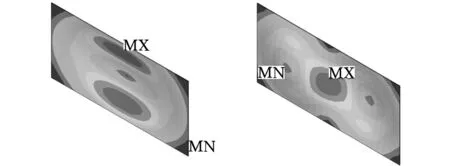
(a)一階振型及應變分布　(b)二階振型及應變分布圖3　模態振型及應變分布圖

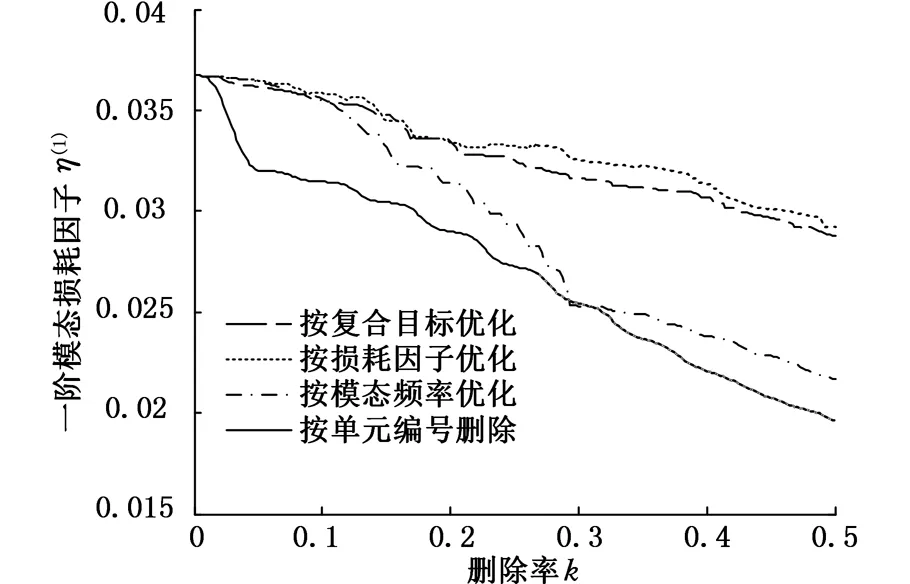
圖5所示為按不同目標進行優化時，損耗因子隨材料刪除率的變化。隨著迭代的不斷進行，刪除率不斷增加，以損耗因子為目標對阻尼材料進行優化布局時，各階次模態損耗因子雖有一定程度下降，但降幅均不大，阻尼結構的減振效果最好。當僅考慮結構模態頻率目標時，結構損耗因子變化較大。當綜合考慮損耗因子和模態頻率時，結構損耗因子變化比較平穩且降幅相對較小。

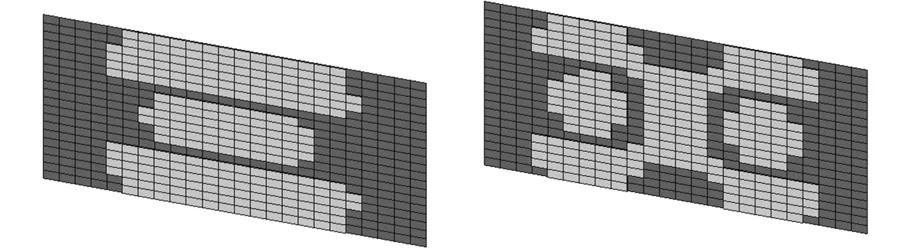
(a)一階復合多目標優化　(b)二階復合多目標優化

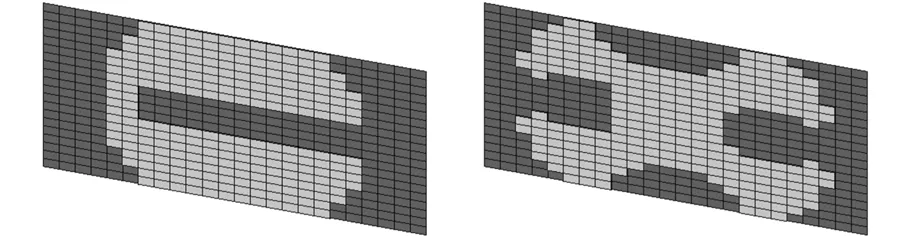
(c)一階損耗因子優化　　(d)二階損耗因子優化

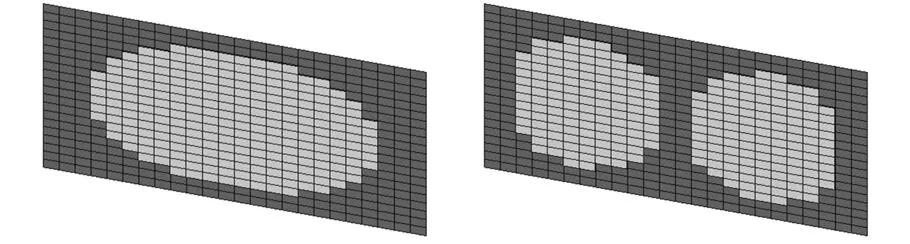
(e)一階模態頻率優化　　(f)二階模態頻率優化圖4　約束阻尼材料優化布局

(a)一階損耗因子迭代

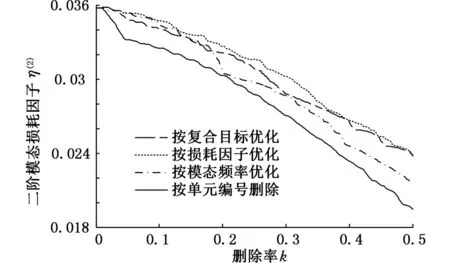
(b)二階損耗因子迭代圖5　約束阻尼模態損耗因子隨刪除率的變化

圖6為基于不同目標優化時，模態頻率隨刪除率變化的曲線。當以損耗因子為目標進行材料優化布局或直接按單元編號順序刪除單元時，隨著優化迭代的不斷進行，約束阻尼結構的模態頻率變化較大。當按頻率目標進行優化時，頻率變動最小。而采用復合目標優化時，結構的頻率變化較以頻率為目標優化時要大，但較其它優化或不優化時情況要小得多。可見，基于復合多目標優化方法進行結構拓撲優化，既可保持結構模態頻率穩定、符合特定階次模態頻率的要求，又能使結構獲得較好的減振效果。

(a)一階頻率迭代(50%)

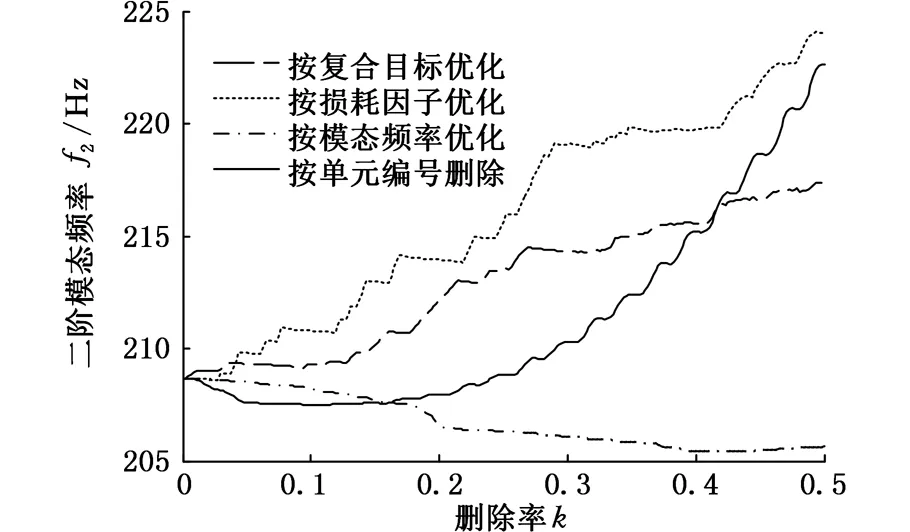
(b)二階頻率迭代(50%)圖6　約束阻尼模態頻率隨刪除率的變化

圖7為約束阻尼結構諧響應分析圖。相比于阻尼材料全覆蓋的結構響應，采用復合目標優化時，對應階次響應幅值均有下降，按損耗因子為目標優化時，結構對應階次響應幅值進一步下降。而按單元編號刪除時，結構一階、二階響應幅值不降反升。通過阻尼結構的諧響應分析對比，驗證了復合多目標漸進拓撲優化方法的可行性。由此可見，基于漸進法對阻尼結構進行優化，結構減振效果顯著。

5　結論

(1)建立了約束阻尼結構有限元動力學模型，推導出基于模態應變能與模態動能的模態損耗因子靈敏度計算式，并推導出模態頻率靈敏度計算式。

(2)構建出以模態損耗最大化、模態頻率變動最小化為目標，以阻尼材料用量為約束的阻尼板多目標動力學優化數學模型。

(3)采用拓撲漸進法求解動力學優化模型，基于歸一化復合靈敏度編程實現了約束阻尼板動力學優化。

(4)采用多目標拓撲漸進法進行阻尼板減振優化，既可大幅提高阻尼材料的減振效能，又能保證阻尼板動力學特性的穩定性，還能大量減小阻尼材料用量。

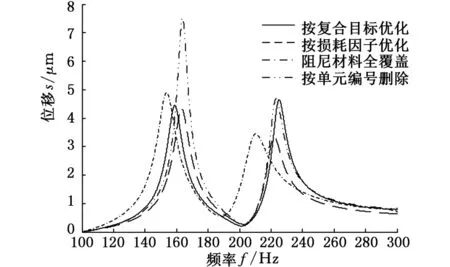
(a)一階模態優化后的諧響應

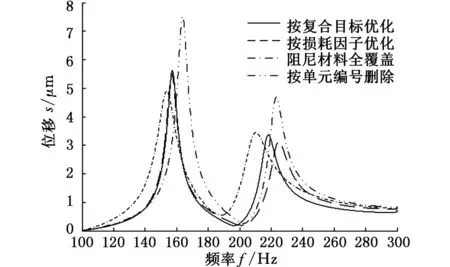
(b)二階模態優化后的諧響應圖7　阻尼結構頻響特性

[1]常冠軍.黏彈性阻尼材料[M].北京: 國防工業出版社，2012.

[2]楊德慶，柳擁軍. 自由阻尼層結構阻尼材料配置優化的拓撲敏度法[J]. 振動工程學報, 2003,16(4):420-425.

YangDeqing,LiuYongjun.TopologicalSensitivityMethodfortheOptimalPlacementofUncon-strainedDampingMaterialinStructures[J].JournalofVibrationEngineering，2003,16(4): 420-425.

[3]張志飛，倪新帥，徐中明，等. 基于優化準則法的自由阻尼材料拓撲優化[J]. 振動與沖擊, 2013,32(14)：98-102.

ZhangZhifei,NiXinshuai,XuZhongming,etal.TopologicOptimizationofaFreeDampingMaterialBasedonOptimalCriteriaMethod[J].JournalofVibrationandShock， 2013,32(14)：98-102.

[4]王明旭，陳國平. 基于均勻化方法的約束阻尼柱殼結構動力學性能優化[J]. 中國機械工程, 2011,22(8):892-897.

WangMingxu,ChenGuoping.DynamicsPerformanceOptimizationofCylindricalShellwithConstrainedDampingLayerUsingHomogenizationApproach[J].ChinaMechanicalEngineering, 2011,22(8):892-897.

[5]李攀，鄭玲，房占鵬. SIMP插值的約束層阻尼結構拓撲優化[J]. 機械科學與技術, 2014, 33(8): 1122-1126.

Li Pan, Zheng Ling, Fang Zhanpeng. Topology Optimization of Constrained Layer Damping Structure Based on SIMP Interpolation Method[J]. Mech-anical Science and Technology for Aerospace Engi-neering, 2014, 33(8): 1122-1126.

[6]李亞娟, 吳光強.基于聲靈敏度的車身拓撲優化[J]. 計算機輔助工程, 2009,18(4):15-18.

Li Yajuan, Wu Guangqiang. Topology Optimizati-on of Car Body Based on Acoustic Sensitivity[J]. Computer Aided Engineering, 2009,18(4):15-18.

[7]郭中澤，陳裕澤. 基于準則法的阻尼結構拓撲優化[J]. 宇航學報, 2009, 30(6): 2387-2391.

Guo Zhongze, Chen Yuze. Topology Optimization of the Damping Structure with Optimal Criteria[J]. Journal of Astronautics, 2009, 30(6): 2387-2391.

[8]趙冬艷，石慧榮. 基于遺傳算法的約束阻尼梁減振優化分析[J]. 力學與實踐，2011, 33(4):13-16.

Zhao Dongyan, Shi Huirong. Reduction of Vibration and Optimization of Beams with Constrained Layer Damping Patch Based on Genetic Algorithm[J]. Mechanics in Engineering，2011, 33(4):13-16.

[9]Zheng H, Tan X M. Damping Analysis of Beams Covered with Multiple PCLD Patches[J]. International Journal of Mechanical Science , 2006, 48(12): 1371-1383

[10]Xie Y M，Steven G P. Evolutionary Structural Optimization [J]. Computers & Structures, 1996, 58(6): 1067-1073.

[11]韋勇．阻尼結構的建模、識別和拓撲優化研究[D]. 南京：南京航空航天大學，2006.

[12]茅志穎. 結構動力學設計漸進優化方法研究[D]. 南京：南京航空航天大學，2010.

[13]Sigmund O，Petersson J. Numerical Instabilities in Topology Optimization: a Survey on Procedures Dealing with Checkerboard, Mesh Dependencies, Local Minima[J].Strucaural Optimization, 1998, 16: 68-75.

(編輯王旻玥)

Topological Multi-objective Dynamics Optimization of Constrained Damping Structure Based on Evolutionary Structural Optimization

He HonglinTao JieLiu YaodiLing Pu

Nanchang Hangkong University , Nanchang, 330063

Aimed to realize vibration reduction of damping structure，constrained damping plate vibration optimization was studied. From the constitutive relations of damping materials, the dynamics equation of constrained damping plate was deduced by principle of virtual work, modal loss factor mathematical calculation formula was deduced based on the energy dissipation. A modal was built, which took maximum the modal loss factor and minimum modal frequency changes as the objective function, damping materials consumption as constraint conditions, the modal loss factor and frequency sensitivity formula was deduced, normalized composite sensitivity formula was constructed. Evolutionary structural optimization was introduced to solve the topological optimization mathematical model, A program of damping structure topological optimization process was given in order to realize simulation calculation of damping plates. The simulations show that multi-objective of the evolutionary structural optimization may significantly improve the vibration reduction effectiveness of the damping material, guarantee the stability of frequency characteristics of the damping plates and greatly reduce the dosage of damping materials. The harmonic response analysis was carried out on the damping plates to verify the effectiveness of the optimization results. The optimization method may be widely used in the design of vibration reduction which have strict requirements in structure dynamics characteristics.

constrained damping structure; modal loss factor; modal frequency; dynamics optimization

2015-10-29

國家自然科學基金資助項目(51265040)；江西省自然科學基金資助項目(20122BA216027)

TH113.1；O328

10.3969/j.issn.1004-132X.2016.17.007

賀紅林，男，1967年生。南昌航空大學航空制造工程學院教授。主要研究方向為復雜結構動力學優化、精密驅動技術。陶結，男，1991年生。南昌航空大學航空制造工程學院碩士研究生。劉堯弟，男，1991年生。南昌航空大學航空制造工程學院碩士研究生。凌普，男，1992年生。南昌航空大學航空制造工程學院碩士研究生。