磨齒機分度誤差傳遞規律

凌四營,李　軍,于佃清,賈　穎,王立鼎,,婁志峰

(1.大連理工大學 精密特種加工及微系統教育部重點實驗室，遼寧 大連 116023；2.大連理工大學 微納米技術及系統遼寧省重點實驗室，遼寧 大連 116023；3. 遼寧省計量科學研究院，遼寧 沈陽 110004)

?

磨齒機分度誤差傳遞規律

凌四營1*,李軍2,于佃清3,賈穎2,王立鼎1,2,婁志峰1

(1.大連理工大學 精密特種加工及微系統教育部重點實驗室，遼寧 大連 116023；2.大連理工大學 微納米技術及系統遼寧省重點實驗室，遼寧 大連 116023；3. 遼寧省計量科學研究院，遼寧 沈陽 110004)

為預測被加工齒輪的齒距加工精度，研究了Y7125型大平面砂輪磨齒機系統分度誤差的傳遞規律。采用全閉環測量法對用作角度測量基準的正36面棱體進行了高精度標定；基于該正36面棱體和相對測量法在機提取機床36個等分點系統分度誤差曲線；最后在磨齒機上進行精密磨齒實驗，通過比較齒輪試件的齒距累積偏差與機床原始系統分度誤差的差異，研究機床分度誤差的傳遞規律，并通過實驗得到磨齒機分度誤差傳遞過程中的不確定度。實驗結果表明：采用全閉環測量法標定正36面棱體的測量不確定度達到±0.05；磨齒機系統分度誤差傳遞到被加工齒輪后，齒距累積總偏差由2.1 m增大到2.6 m，相對誤差增加了24%；通過磨齒實驗得到磨齒機分度誤差傳遞過程中的不確定度為±0.6 m。得到的機床分度誤差傳遞規律可用于預測齒輪的齒距累積加工精度，為制定科學的磨齒工藝提供技術支持。

磨齒機;分度誤差;齒距累積偏差;誤差傳遞規律;全閉環測量法

*Correspondingauthor,E-mail:luckling168@163.com

1　引　言

齒輪作為機械零件中重要的基礎件之一，尤其是圓柱漸開線齒輪被廣泛應用于常規機械、地面交通、船舶、航空航天、兵器、精密機床與儀器等領域。2014年我國生產齒輪400萬噸，銷售收入2 180億元。中國齒輪的產量居世界首位，但主要以中低端產品為主，高端關鍵齒輪還依賴進口。標準齒輪的制造水平是國家精密齒輪制造水平的重要標志。我國標準齒輪檢定規程JJG 1008-2006中規定：標準齒輪的精度等級是根據單個齒距偏差fpt、齒距累積總偏差Fp、齒廓總偏差Fα、螺旋線總偏差Fβ和徑向跳動Fr的檢定結果劃分的[1]。其中，與機床分度精度相關的單個齒距偏差fpt和齒距累積總偏差Fp即是齒輪國家標準GB/T 10095.1-2008中規定的必檢項目[2]，也是齒輪國際標準ISO1328-1:2013中的默認檢查項目[3]。可見提高齒輪齒距加工精度的重要性。

與齒輪的齒距累積加工精度和單一齒距加工精度密切相關的是機床分度系統精度。目前，高精度的分度系統分為電子直驅分度系統和機械分度系統。其中，機械分度系統根據分度元件的不同，又分為蝸輪蝸桿分度系統、馬氏槽輪分度系統、分度盤式分度系統和端齒分度系統等[4]。其中，端齒分度系統的分度精度最高，一般可達到0.5″，最高可達到0.1″，是機械分度系統中分度精度最高的分度元件[5]；其次是分度盤式分度系統，其分度精度可達5～10″。本文選用的磨齒機床(Y7125)的分度系統為分度盤式分度系統。

為提高被加工齒輪的單個齒距偏差fpt和齒距累積總偏差Fp，本文通過精確提取磨齒機床系統分度誤差曲線，研究了磨齒機床系統分度誤差的傳遞規律，預測齒輪的齒距加工精度，并對制定科學的磨齒工藝提供技術支持。

2　系統分度誤差的提取

2.1分度系統工作原理

Y7125型大平面砂輪磨齒機的分度系統為分度盤式分度系統，分度工作方式為間歇分度，分度示意如圖1所示。

圖1　分度示意圖Fig.1　Sketch map of index

被加工齒輪和分度盤同軸安裝，因此，齒輪的齒距偏差和機床分度系統的誤差值一一對應。只需要提取點數等同于被加工齒輪齒數的離散分度誤差值即可。高精度的全微機化齒輪機床精度檢測分析系統(FMT)和圓感應同步器可滿足磨齒機床系統分度誤差的提取[4,6,7]。根據Y7125磨齒機床的特性與實驗條件，選用經過精確標定的正36面棱體和自準直儀，在機提取磨齒機的36個均布離散點的系統分度誤差值來研究磨齒機分度誤差傳遞規律。

由于1級精度的正36面棱體的分度誤差和磨齒機系統分度誤差在同一數量級上(4～10″)，因此，1級精度的正36面棱體不滿足磨齒機系統分度誤差的測量要求。對實驗室的正36面棱體進行了精確標定，以分離出正36面棱體的系統分度誤差[8]，提高正36面棱體的測量精度。

2.2正36面棱體的標定

利用自準直儀和端齒自動分度臺，采用全閉環測量法標定正36面棱體[9-11]。參考多面體檢定規程[12]，搭建正36面棱體標定平臺如圖2所示。

圖2　正36面棱體的標定Fig.2　Calibration of 36 angular prism mirror

采用全閉環測量法采集端齒自動分度臺和正36面棱體的組合數據矩陣M(36×36)，如圖3所示。

圖3　原始測量數據Fig.3　Initial measuring data

分離出正36面棱體的系統分度誤差柱狀圖如圖4所示。最大分度誤差為4.1″。

圖4　正36面棱體的系統分度誤差柱狀圖Fig.4　Bar graph of indexing error of 36 normal prism

原始測量數據分離出正36面棱體和自動端齒臺的系統誤差后得到的殘差vi,j如圖5所示。根據殘差計算出全閉環測量法的測量不確定度。

圖5　全閉環測量法的殘差Fig.5　Residual error of closure method

根據殘差計算出全閉環測量法的測量不確定度U99=±0.05″。可見，經過全閉環測量法標定的正36面棱體具有較高的測量精度，滿足分度盤式分度系統的測量要求。

2.3系統分度誤差的提取

直接使用1級精度的多面棱體、自準直儀和全閉環測量法能夠實現高精度分度系統的誤差曲線的提取。在機測量時，考慮到數據量(36×36)較大，采集周期較長，溫濕度的變化及儀器零位的漂移等因素會影響測量結果的準確性。為此，采用經過精確標定的正36面棱體和相對測量法直接在機提取磨齒機的系統分度誤差。測量時，斷開機床的展成系統，利用機床間歇自動分度的特點，在磨齒工作狀態下，間歇采集機床分度系統的分度誤差值；正36面體棱體的安裝位置即為齒輪試件的加工位置。正36面棱體的0°與磨齒機床分度的0°和180°兩個對稱位置分別對齊，多次測量取平均值，以消除棱體安裝偏心對測量結果的影響。磨齒機床系統分度誤差在機測量平臺如圖6所示。

圖6　磨齒機床系統分度誤差的在機提取Fig.6　Extraction the systematic indexing error of gear grinding machine

最終提取Y7125磨齒機36點系統分度誤差E0曲線如圖7所示。分度系統36點的最大累積分度誤差為6.8″。

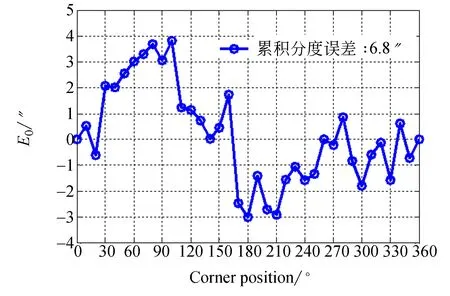
圖7　磨齒機分度系統誤差曲線Fig.7　Systematic indexing error curve of the gear grinding machine

3　誤差傳遞規律研究

3.1磨齒實驗

Y7125磨齒機分度系統如圖8所示。

圖8　磨齒機分度系統Fig.8　Indexing system of gear grinding machine

被磨齒輪和分度盤都安裝在加工主軸上，如果沒有安裝偏心誤差，分度盤、加工芯軸和被磨齒輪將具有統一的回轉軸線。理論上分度系統的誤差將1∶1的傳遞給被加工齒輪。為了減小齒輪試件安裝偏心對齒距偏差的影響，試驗中采用徑向可調式芯軸及密珠軸套定位。

選擇如表1所示參數的齒輪試件，在(20±1) ℃的恒溫室里進行精密磨齒實驗，如圖9所示。

表1　試件齒輪參數

圖9　磨齒實驗Fig.9　Experiment of gear grinding

然后在(20±1) ℃的恒溫室，在自行設計的超精密齒距測量裝置上進行精密對試件的齒距偏差進行精密測試[13-14]。得到的試件齒距累積偏差(Fpi)曲線與機床原始系統誤差曲線進行比較如圖10所示。為了便于比較，將單位(″)轉換成齒輪分度圓(d=126 mm) 上的位移μm。

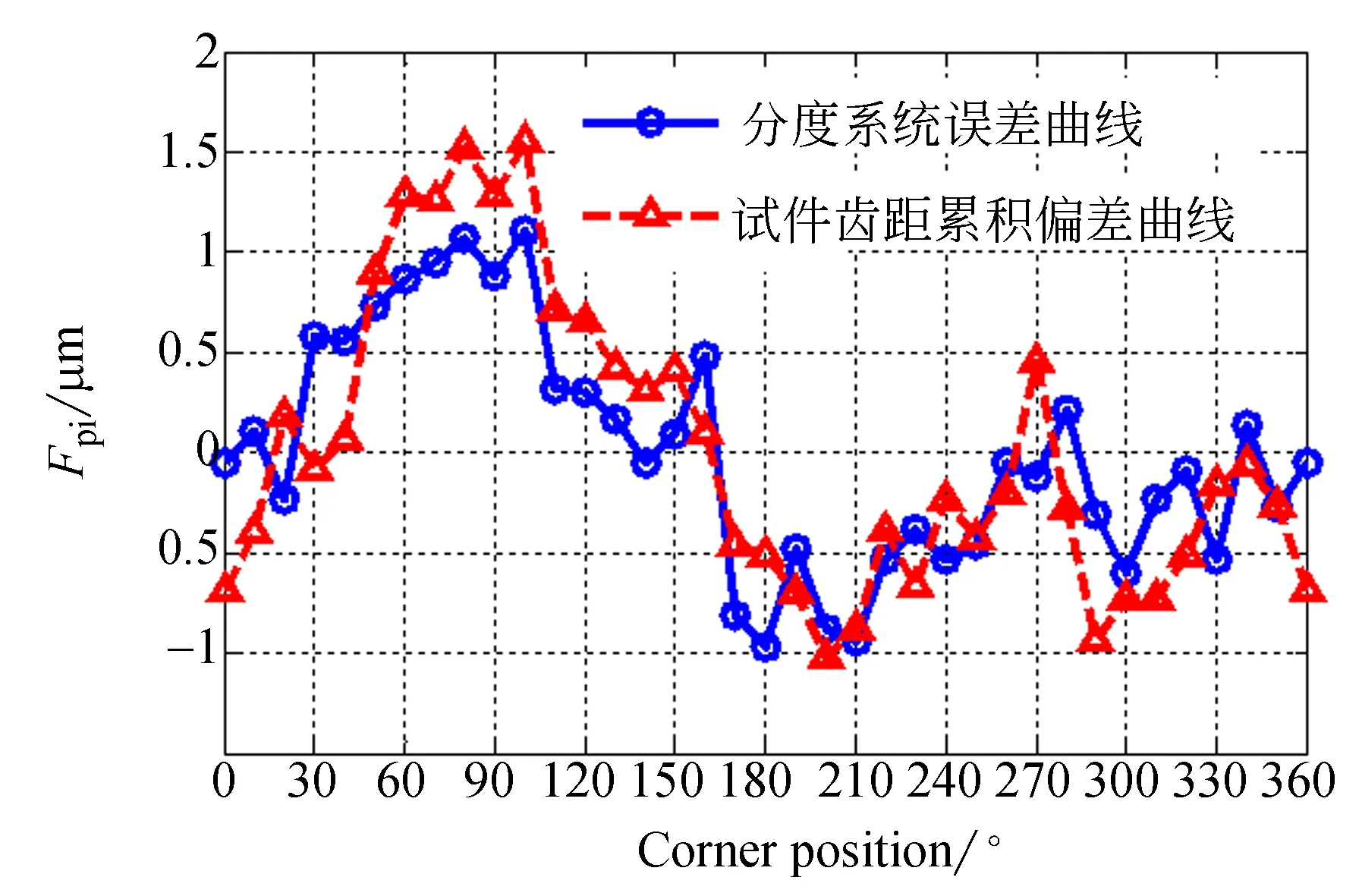
圖10　磨齒機系統分度誤差傳遞規律Fig.10　Indexing error transfer law of gear grinding machine

由圖10可知，被加工齒輪的齒距累積偏差曲線與磨齒機分度系統的誤差曲線變化趨勢基本一致，但有增大的趨勢。磨齒機分度系統36點的最大累積誤差(6.8″)折算到齒輪分度圓為2.1 μm，而被加工齒輪的齒距累積總偏差Fp為2.6 μm，齒距累積總偏差增大了約24%。

3.2誤差傳遞過程中的不確定度

試件齒距累積偏差曲線與機床原始系統分度誤差的差異(如圖11所示)反映出了磨齒機床分度誤差傳遞過程中的不確定度。

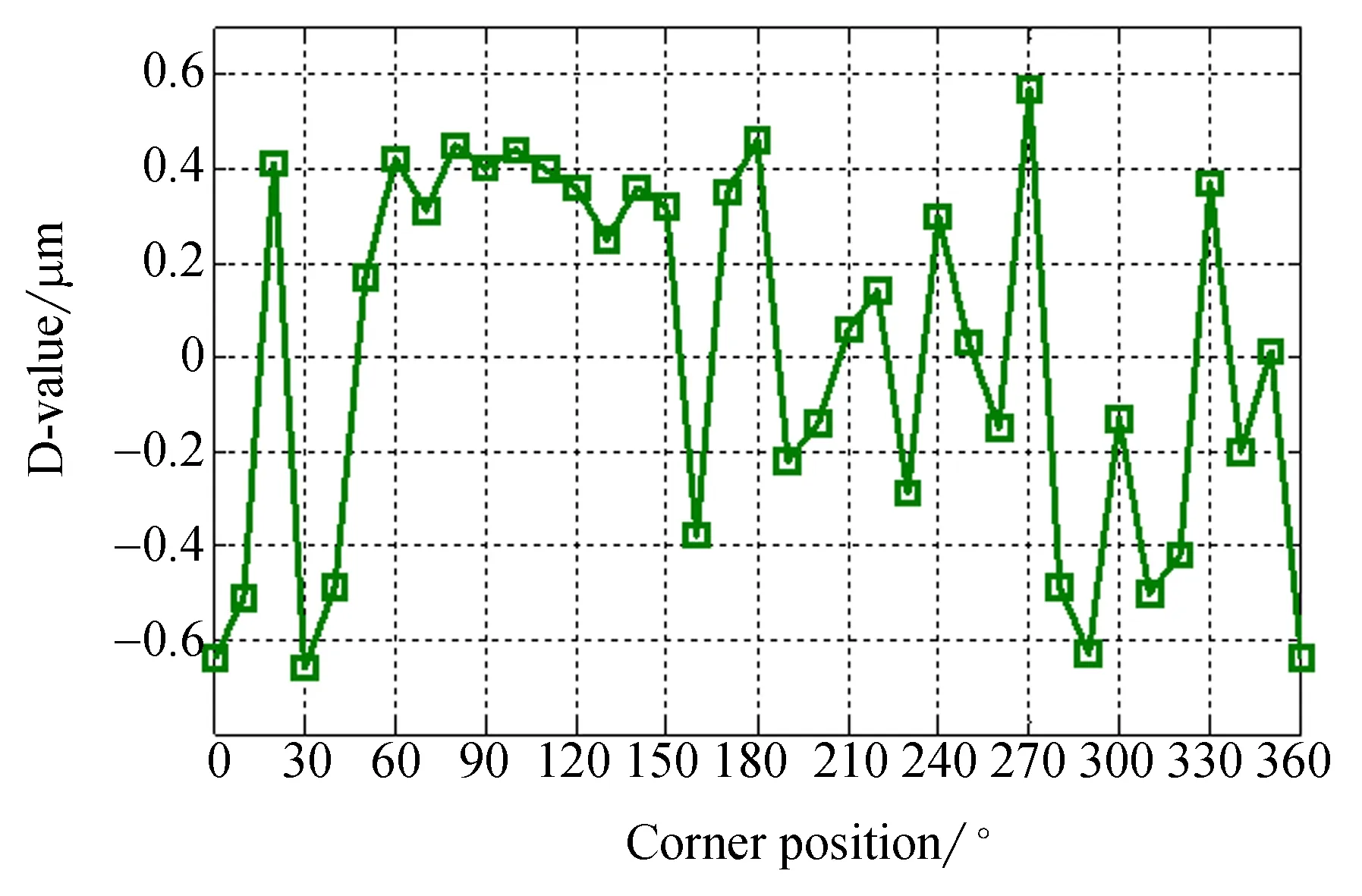
圖11　分度誤差傳遞規律Fig.11　Indexing error transfer law

由圖11可知，分度誤差差值曲線在±0.6 μm內變化且沒有明顯的一次諧波分量，說明齒輪試件沒有明顯的安裝偏心誤差。也說明采用徑向可調式芯軸及密珠軸套具有較高的定位精度。此外，該曲線中的偏差值具有一定的不確定度。測量過程中的阿貝誤差、測量系統誤差等，加工過程中的精加工時刻的選擇、進刀量與進刀時刻的均勻性、砂輪的品質、光整加工周期的長短、定位爪卡入齒槽的狀態、加工主軸的扭轉振動、加工環境因素、磨齒工藝、工件的表面粗糙度等因素都會影響齒輪的齒距加工精度，致使磨齒機床系統分度誤差傳遞到被加工齒輪上后有變大的趨勢。

磨齒機分度誤差傳遞過程中的不確定度是該機床加工齒輪齒距指標的綜合體現。該值越小，說明機床的加工性能越優越。通過磨齒機床的原始系統分度誤差和磨齒機分度誤差傳遞過程中的不確定度，可預測齒輪的齒距加工精度。并對制定科學的磨齒工藝提供技術支持。

4　結　論

本文采用全閉環測量法對正36面棱體進行了高精度標定，標定的測量不確定達±0.05″；采用經過全閉環測量法標定的正36面棱體和相對測量法在機精確提取了機床36個均布離散點的系統分度誤差曲線，最大分度誤差為6.8″；通過精密磨齒實驗研究磨齒機系統分度誤差的傳遞規律。磨齒機床系統分度誤差傳遞到被加工齒輪后，齒距累積總偏差由2.1 μm增大到2.6 μm，相對誤差增加了約24%。通過實驗方法得到了特定工況下機床分度誤差傳遞過程中的不確定為±0.6 μm。根據機床原始系統分度誤差及磨齒機分度誤差傳遞過程中的不確定度可預測齒輪的齒距加工精度。

[1]JJG-1008-2006，標準齒輪[S].

JJG-1008-2006，Master gears [S]. (in Chinese)

[2]GB/T 10095.1-2008，圓柱齒輪精度制—第1部分：輪齒同側齒面的檢驗[S].

GB/T 10095.1-2008，Cylindrical gears- system of accuracy-Part 1：Definitions and allowable values of deviations relevant to corresponding flanks of gear teeth [S]. (in Chinese)

[3]ISO1328-1:2013，Cylindrical gears-ISO system of flank tolerance classification-Part 1：Definitions and allowable values of deviations relevant to flanks of gear teeth[S].

[4]彭東林，鄭 永，陳自然，等. 基于誤差傳遞理論及誤差修正技術的高精度蝸輪母機研制[J]. 機械工程學報，2011，47(9)：157-163.

PENG D L，ZHENG Y，CHEN Z R，etal.. Research of high-precision worm gear machine tool based on error transmission theory and error correction technique[J].JournalofMechanicalEngineering，2011，47(9)：157-163. (in Chinese)

[5]王立鼎，凌四營，王曉東，等. 磨齒機用高精度端齒自動分度裝置[P].中國:ZL200910309243.2，2011-01-05.

WANG L D，LING S Y，WANG X D，etal.. High precision end tooth automatic indexing device for grinding machine[P]. China:ZL200910309243.2，2011-01-05.

[6]孫世政，彭東林，鄭方燕，等. 時柵傳感器動態測量誤差補償[J]. 光學 精密工程，2015，23(4)：1114-1121.

SUN SH ZH，PENG D L，ZHENG F Y，etal.. Compensation for dynamic measurement errors of time grating sensor [J].Opt.PrecisionEng.，2015，23(4)：1114-1121. (in Chinese)

[7]袁輝，劉朝暉，李治國，等. 圓感應同步器系統誤差的動態提取與補償[J]. 光學 精密工程，2015，23(3)：794-802.

YUAN H，LIU CH H，LI ZH G，etal.. Dynamic extracting and compensating of system error for rotary circular inductosyn [J].Opt.PrecisionEng.，2015，23(3)：794-802. (in Chinese)

[8]盧榮勝，李萬紅，勞達寶，等. 激光跟蹤儀測角誤差補償[J]. 光學 精密工程，2014，22(9)：2229-2305.

LU R SH，LI W H，LAO D B，etal.. Angular error compensation for laser tracker [J].Opt.PrecisionEng.，2014，22(9)：2229-2305. (in Chinese)

[9]KNIEL K，HARTIG F，OSAWA S，etal.. Two highly accurate methods for pitch calibration [J].MeasurementandScienceTechnology，2009，20(11)：115110.

[10]SATO O，OSAWA S，KONDO Y，etal.. Calibration and uncertainty evaluation of single pitch deviation by multiple-measurement technique [J].PrecisionEngineering，2010，34(1)：156-163.

[11]LING S Y，LOU ZH F，WANG L D. Closure measuring technique on the datum of an end-tooth indexing table [J].MeasurementScienceandTechnology，2012，23(4)：045006.

[12]JJG-238-2007，正多面棱體[S].

JJG-238-2007，Angular polygon [S]. (in Chinese)

[13]LOU Z F，LING S Y，HE H ZH，etal.. A kind of multi-step method for measuring pitch deviation of a gear [J].MeasurementandScienceTechnology，2012，23(11)：115002.

[14]婁志峰，賀海釗，凌四營，等. 齒距偏差測量中系統誤差的分離方法[J]. 納米技術與精密工程，2012，10(6)：537-540.

LOU ZH F，HE H Z，LING S Y，etal.. Separation method of systematic errors in pitch deviation [J].MeasurementNanotechnologyandPrecisionEngineering，2012，10(6)：537-540. (in Chinese)

凌四營(1978-)，男，山東日照人，副教授，碩士生導師，2002年于山東交通學院獲得學士學位，2007年于山東理工大學獲得碩士學位，2013年于大連理工大學獲得博士學位，主要從事精密機械設計、超精密磨齒工藝與測試技術等方面的研究。E-mail：luckling168@163.com

李軍(1993-)，男，安徽滁州人，碩士研究生，2015年于南通大學獲得學士學位，主要從事齒輪測量儀器的設計與測試技術等方面的研究工作。E-mail：708849084@qq.com

(版權所有未經許可不得轉載)

Indexing error transfer law of a gear grinding machine

LING Si-ying1*，LI Jun2，YU Dian-qing3，JIA Ying2，WANG Li-ding1, 2，LOU Zhi-feng1

(1.KeyLaboratoryforPrecision&Non-traditionalMachiningoftheMinistryofEducation，DalianUniversityofTechnology，Dalian116023,China； 2.KeyLaboratoryforMicro/NanoTechnologyandSystemofLiaoningProvince，DalianUniversityofTechnology，Dalian116023,China； 3.LiaoningResearchInstituteofMetrology，Shenyang110004,China)

To predict the pitch machining accuracy of a gear to be ground, the transfer law of the systematic indexing error of the gear-grinding machine (Y7125) with flat-faced grinding wheel was researched. The normal 36 prism for angle measurement datum was calibrated in high-precision by using the full closure measurement method, then the systematic indexing error curve with 36 equal points was extracted on-machine based on the normal 36 prism and the relative measurement method. Finally, the precision gear-grinding experiment was conducted on the gear-grinding machine. The indexing error transfer law of the machine was studied by comparing the difference between the cumulative pitch deviation of a gear specimen and the original systematic indexing error of the gear grinding machine, and the uncertainty during the error transfer process of the gear-grinding machine was obtained by experiments. Experimental results show that the measurement uncertainty of the full closure measurement method to calibrate the normal 36 prism reaches to 0.05″.The total cumulative pitch deviation varies from 2.1 μm to 2.6 μm and the relative error increases by 24% after the systematic indexing error of the gear grinding machine transfers to the gear to be ground. Moreover, the uncertainty during the error transfer process is ±0.6 μm. The transfer law of systematic indexing error of the gear-grinding machine from the experiments mentioned above can be used to predict the pitch machining accuracy of the gear to be ground and can provide technical supports for the development of the scientific gear-grinding process.

gear-grinding machine；indexing error；cumulative pitch deviation；error transfer law ; full closure measurement method

2016-02-20；

2016-03-15.

國家自然科學基金青年基金資助項目(No.51305059)；國家自然科學基金重點資助項目(No.U1508211)；國家自然科學基金創新研究群體資助項目(No.51321004)；國家科技支撐計劃資助項目(No.2014BAF08B)

1004-924X(2016)08-1934-06

TG 86；TG 616

A

10.3788/OPE.20162408.1934