基于模型優化的Android平臺虛擬加工系統設計
褚人宇 施 群 游玉霖
(上海大學機電工程與自動化學院,上海 200072)
?
基于模型優化的Android平臺虛擬加工系統設計
褚人宇施群游玉霖
(上海大學機電工程與自動化學院,上海200072)
針對移動平臺上實現虛擬加工仿真需要解決仿真模型數據量過大及仿真效果差的問題,提出了基于STL簡化的三角模型及優化Z-Map算法。該算法適用于五軸數控加工,提高了仿真程序運行效率;同時給出了Z-Map網格優化方法,保證了系統在移動平臺上的運行效果。在Android平臺上搭建了虛擬加工仿真系統。試驗結果驗證了該算法在Android平臺上與虛擬加工結合的可行性以及良好的仿真效果。
移動平臺STL模型Android平臺Z-Map算法計算機仿真虛擬制造虛擬加工五軸加工
0 引言
虛擬制造是在計算機上執行產品設計及制造的全過程[1]。虛擬模型可以在產品制造前對產品的性能和可制造性等問題進行預測及分析[2]。隨著虛擬制造概念的提出[3],虛擬加工仿真技術[4]也得到了很大的發展。而隨著智能制造時代的到來,各種移動設備在人們日常辦公中發揮的作用也越來越大。在機械制造領域,很少看到計算機仿真技術在這些移動平臺上的應用。Android系統在移動平臺終端的市場占有率超過70%。本文提出并開發了基于Android操作系統的虛擬加工仿真系統。
1 仿真系統模型構建存在的問題
Android操作系統的計算能力以及圖形顯示能力較弱,基于Android平臺的虛擬加工系統設計需要解決如下問題。
①由于機床三維模型的構造較為復雜,模型數據文件較大,在移動平臺中直接讀取、顯示,占用的內存較大。而且在仿真過程中,需要實時刷新機床數據,數據量過大會明顯影響程序運行的效果,以及切削加工時機床實時顯示的連續性。在虛擬仿真系統中,機床模型采用光圈化立體造型(sterelitho graphy,STL)數據模型,采用三角片精簡技術對模型數據進行處理,可以減少數據量。江本赤等[5]分析了STL模型中一些狹長的鈍角三角形對模型精度的影響,并對這類三角形進行過濾。這種方法對于三角片網格比較均勻的STL模型簡化效率較低。閆濤等[6]通過計算三角片權重并排序,刪除了權重較小的三角片,并對剩余三角片進行重構。Schroeder[7]提出了頂點刪除法的基本思想,其主要思想是判斷頂點對模型的重要程度,對不重要的頂點進行刪除。本文在頂點刪除法的基礎上,提出了STL模型優化算法。
②仿真加工的效率成為研究過程中選擇仿真模型構造方法主要考慮的因素。實體構造幾何法[8]最早是由Voelcker和Hunt提出的。該方法表示簡潔,但是需要進行大量的布爾運算,存在計算量過大的問題。為了解決實體構造幾何法計算量過大的問題,Van Hook[9]提出了Z-buffer結構,具體是將刀具按屏幕像素離散成Z-buffer結構,切削則可以簡化成一維運算,大大提高了運算效率。Hsu PL[10]和Choi KB[11]將Z-buffer結構拓展,提出了Z-Map的思想,并對該方法的應用進行了介紹,證明Z-Map方法可以避免布爾運算,大大提高了仿真效率。王鵬遠[12]將離散的工件模型沿著Z方向投影,進而離散成Z方向的線段。起點為投影底面的網格點,終點為模型頂面上的點,并將其應用于三軸仿真加工系統,獲得了不錯的仿真效果。郝大功[13]等提出了基于Z方向誤差的Z-Map 模型簡化算法,對Z-Map模型的網格進行了精簡,提高了仿真效率,但是仿真效果并不理想。
以上文獻中的Z-Map只是應用于三軸加工,并沒有向五軸拓展。五軸加工的多是自由曲面,而自由曲面加工仿真的效果與網格劃分的方式息息相關。若網格劃分比較密集,則數據量和運算量都較大,仿真效率低。若網格劃分比較稀疏,則采用Z-Map方法獲取的加工表面較為粗糙,仿真顯示效果差。加工仿真過程中,為了解決這一矛盾,本文提出了一種五軸自適應Z-Map模型。
2 基于STL模型優化算法
先對STL模型進行分界區處理,再對分割完成后的區塊進行精簡,得到精簡后的STL數據。為了便于算法的描述,我們先對STL模型進行如下集合定義:STL模型是點、線、面的集合,由一個頂點出發,建立三角片各個基本元素的直接聯系。三角片分區塊示意圖如圖1所示。
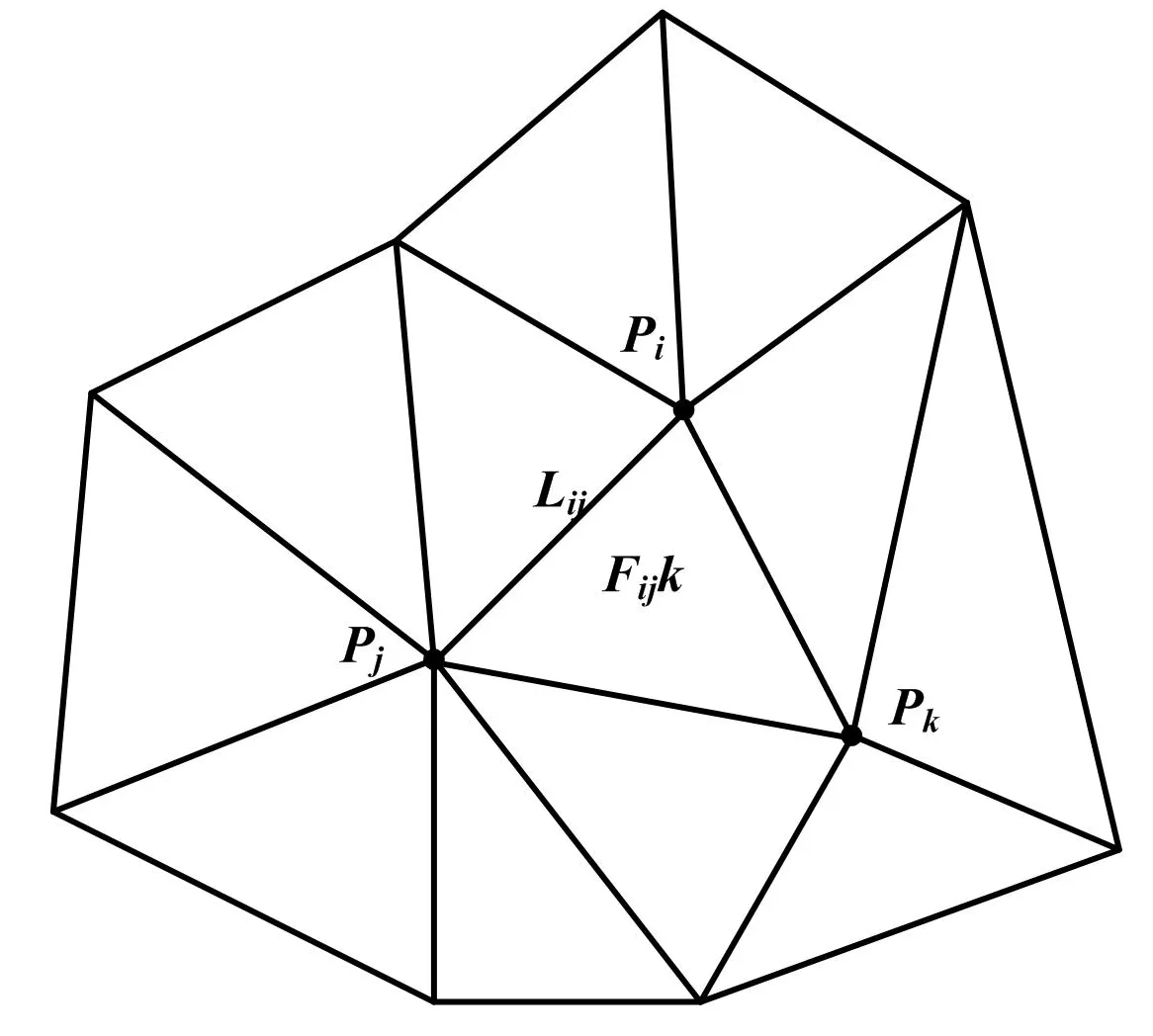
圖1 三角片分區塊示意圖
三角片模型由一個頂點Pi出發,建立其與線Lij和面Fijk的聯系。
三角片精簡具體算法流程如下。
①因為模型邊界的改變會直接影響簡化后模型的形狀特征,故先對STL模型進行邊界提取,判斷三角片各個邊是否存在共邊的情況。設公共邊的端點編號分別為i、 j,判斷是否存在包含公共邊的不同三角片。若滿足條件,則該邊為公共邊;若不存在,則該邊為模型邊界,予以保留。
②判斷STL模型分區塊是否平坦,若平坦,則標記對應的三角片數據;若不平坦,則保留該區域原有三角片數據。以一個三角片ΔPiPjPk為中心,與中心三角片有共同頂點的三角片共同構成一個分區,作為一塊判斷區域。
判斷每個區塊是否平坦,本文提出了一種以相鄰三角片法向量加權方差值作為判斷區域平坦的依據。不僅相鄰三角片法向量夾角對平面的平坦度有影響,三角片的大小也對分區塊的平坦度有較大的影響,這里引入加權方差作為判斷分區塊平坦度的依據。
以相鄰三角片面積A1與中心三角片面積A0的比值作為權值w:
(1)
定義中心三角片與相鄰三角片之間的夾角為θ,中心三角片的法向量為n0,相鄰三角片的法向量為n1,則可根據以下公式計算夾角θ:
(2)
加權方差值D(wθ)為:
D(wθ)=E(wθ)2-E2(wθ)
(3)
式中:E(wθ)為分區塊中法向量的加權平均值。
方差值本身就能夠反映隨機變量波動程度,增加加權值后更能準確描述三角片區域的曲率波動情況。根據分區塊三角片的加權均方差是否小于給定閾值σ,判斷分區塊平坦情況。
③刪除平坦分區塊中心三角形中重要程度較低的頂點,并且重新構造三角片。
平坦分區塊中,相對不重要的頂點(形狀較為平坦的頂點)的判斷依據是頂角法向量與共用該頂點的所有三角片法向量的夾角的方差。若方差越大,則頂角越尖銳;反之,則頂角越平坦。
頂點單位法向量nPi計算公式為[14]:
(4)
式中:Fk為包含目標頂點Pi的三角片;γk為三角片在頂點Pi處的頂角;Af k為面Fk的面積;nf k為三角片的法向量;m為共頂點三角片的個數。
(5)
式中:αk為相鄰三角片與頂點單位法向量的夾角;nPi為頂點單位法向量;nk為頂點鄰接三角片法向量。
方差值D(α)為:
D(α)=E(α)2-E2(α)
(6)
式中:E(α)為頂點法向量與鄰接三角片法向量的夾角平均值。
計算平坦分區塊中心三角形頂點處的D(α)值。該值最小的頂點為最不重要的頂點,可刪除并重構三角片。
重構三角片的方法如下:將去除頂點后的鄰接三角片按順序編號,分別編號Pi,Pi+1,Pi+2,…,Pi+n;分別求取間隔一個點的兩個頂點之間的距離,找出其中最小的,連接組成一個三角片;再對剩余的頂點重新按順序編號,繼續尋找兩線距離最短的兩個點,構成三角片,直至所有三角片重構完成。
3 五軸自適應Z-Map模型
3.1五軸Z-Map求交算法
Z-Map方法之前主要應用于三軸加工,結合五軸加工的特點,提出適用于五軸加工的Z-Map算法。用如下的數據結構來表示將Z-Map離散后的線段參數:
publicclassZ-MapLines{
floatstartZ;
//Z-Map線段的起點
floatendZ;
//Z-Map線段的終點
}
publicclassZ-MapLineList{
floatx;
//Z-Map點對應投影點的x坐標
floaty;
//Z-Map點對應投影點的y坐標
List
//儲存每個投影點上對應的線段及其屬性
intm_LineTotally;
// 單一投影點上對應的Z-Map線段的條數}
首先,建立刀具的數學模型。由于刀具在加工時繞軸線旋轉,則可以用回轉體描述刀具的數學模型。若刀具為平底刀,則刀具的數學模型可以表示為圓柱體。本文以C-A雙擺五軸機床為例,進行公示推演。以下公式中:I、J、K分別為刀具的矢量方向的三個分量;X、Y、Z分別為刀具上的坐標點;θ為圓周的角度;r為刀具半徑;n為刀具模型上切削刃的長度;C和A分別為繞Z和X軸的旋轉角度;TX、TY、TZ分別為刀具的刀尖點坐標。
當I≠0、J≠0時,在空間中的任意圓的參數方程可以用式(7)~式(9)表示。由上文可知,空間內刀具模型為圓柱面模型,由圓的參數方程可以推導出刀具圓柱面的參數方程如式(11)~式(12)所示。
x=rcosθ
(7)
y=rsinθ
(8)
z=0
(9)
X=cosC×x+sinC×(cosA×y-sinA×z)+In+TX
(10)
Y=-sinC×x+cosC×(cosA×y-sinA×z)+Jn+TY
(11)
Z=sinA×y+cosA×z+Kn+TZ
(12)
將式(7)~式(9)代入式(10)和式(11),得:
X=cosC×r×cosθ+sinC×cosA×r×sinθ+In+TX
(13)
Y=-sinC×r×cosθ+cosC×cosA×r×sinθ+Jn+TY
(14)
聯立式(12)~式(14),求解:
(15)
當刀具模型與Z-Map線段求交過程中,一個Z-Map模型對應的投影點在Z方向上只存在一條線段,其考慮情況如下。
情況一:當Z-Map投影點的Z向射線與刀具模型沒有交點,此時刀具與被加工物體并未發生接觸,因此不發生切削。
情況二:當Z-Map投影點的Z向射線與刀具相交后產生一個交點,該交點小于Z-Map線段的最高點的值,大于Z-Map線段的最低點的值,此時刀具與被加工物體發生切削。將Z-Map線段的終點值endZ0修改為兩個求得的交點中較小的值。
情況三:當Z-Map投影點的Z向射線與刀具相交后,兩個交點的值均在Z-Map線段的最高點的值和最低點值之間,此時刀具與被加工物體發生切削,并且在同一個Z-Map點出現了兩條Z-Map線段。這時增加線段并設其端點為(endZ1,startZ1),同時對原有線段進行修改,使得endZ0=ArrayZ1、endZ1=endZ62、startZ2=ArrayZ2。
情況四:當Z-Map投影點的Z向射線與刀具相交后產生一個交點,該交點大于Z-Map線段的最低點的值,小于Z-Map線段的最高點的值,此時刀具與被加工物體發生切削,將Z-Map線段的startZ0修改為ArrayZ2。
在刀具與毛坯直線段求交的過程中,一個投影點對應的Z空間方向上有多條線段,可以具體分析每一條線段。具體分析與上文相同。
刀具與Z-Map模型相交情況如圖2所示。
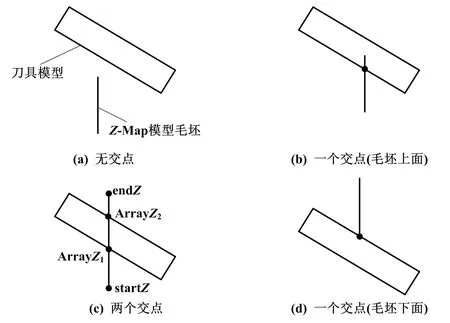
圖2 刀具與Z-Map模型相交情況示意圖
3.2Z-Map自適應網格劃分
定義網格頂點的適應度為λ,表示單個網格頂點與Z-Map模型加工表面的適應程度。
(16)
式中:ΔZi為網格頂點與相鄰的Z-Map網格點在Z方向上的差值。
Z-Map自適應優化流程如圖3所示。

圖3 自適應優化流程圖
自適應優化流程具體說明如下。
①設定網格適應度閾值,該閾值體現了Z-Map模型與真實加工面的偏差程度。
②獲取完成切削區域網格。五軸加工的切削過程可以被看作是多個相鄰刀位的集合,前一個刀位切削到而后一個刀位沒有切削到的區域就是已加工區域。刀具切削區域在網格上的投影如圖4所示,陰影區域為切削過程中已完成的切削部分。
③計算Z-Map網格頂點適應度,以網格四個頂點的適應度均值作為頂點包圍的網格適應度。
④對網格適應度不滿足要求的閾值進行自適應優化。具體方法是選取Z向差值最大的網格邊進行二等分,如此反復,直至所有網格點滿足適應度要求。
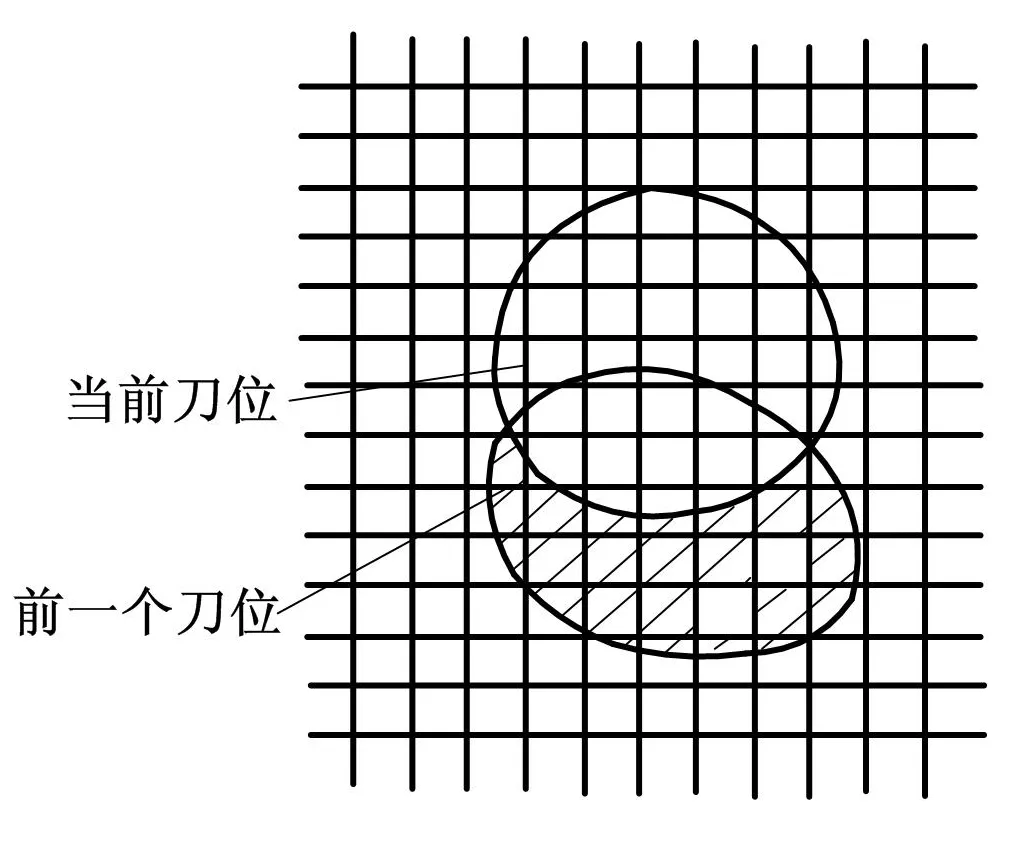
圖4 刀具切削區域在網格上的投影圖
4 試驗驗證
根據上文所述,本文提出的基于Android的五軸數控加工仿真系統搭建流程如圖5所示。
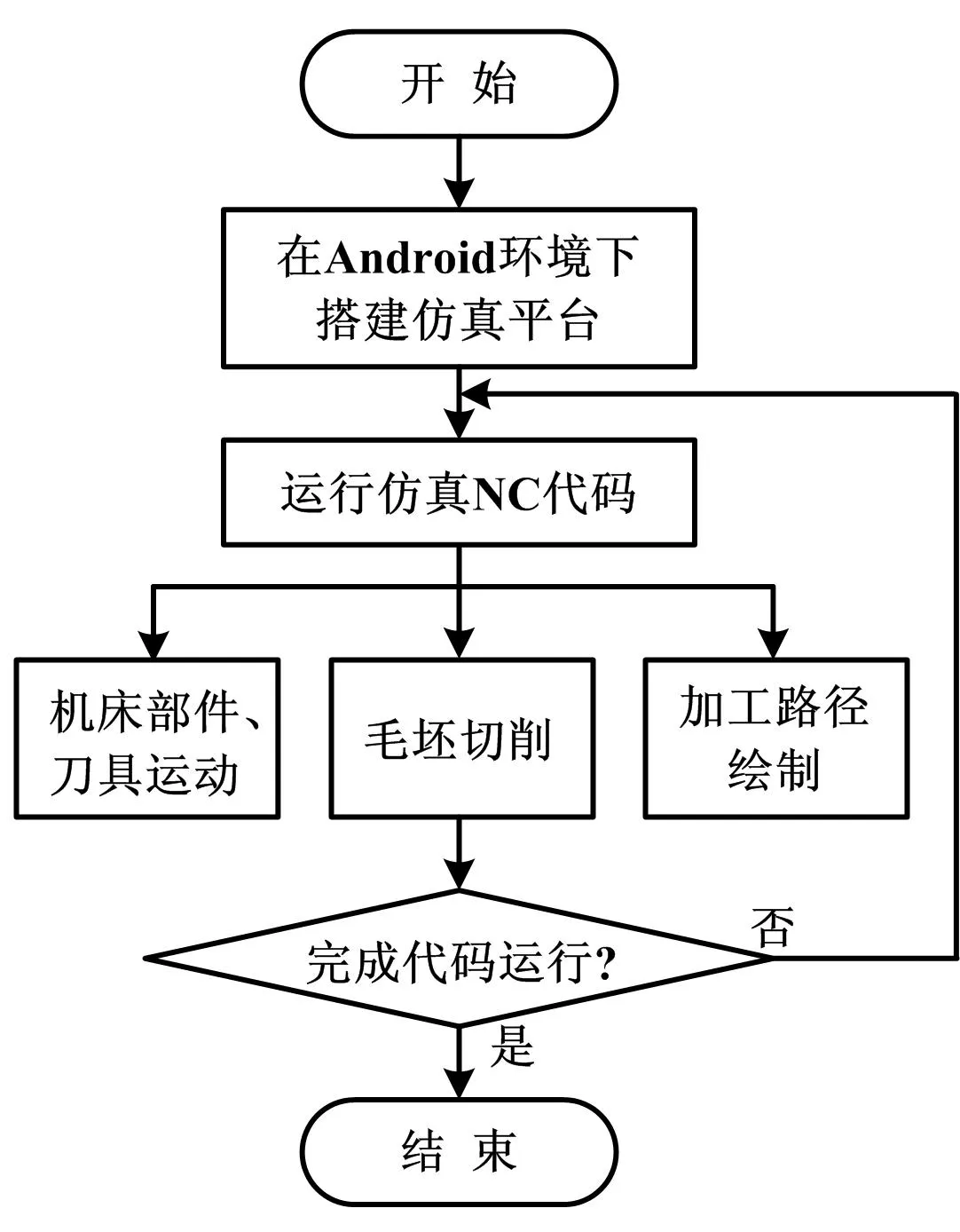
圖5 虛擬仿真系統搭建流程圖
虛擬仿真系統是基于OpenGLES,在Android環境下開發的。試驗平臺為三星N7100移動端搭載基于Android4.1的Flyme2.0深度操作系統。文件讀取及操作方式采用JAVA標準I/O庫。
機床模型數據量大,導入仿真平臺需要一定的加載時間。經過文中STL模型優化精簡方法,確定平坦度加權方差閾值為0.1,篩選次數為2次,可獲得機床主軸外殼的三角片個數對比。精簡前三角片個數為1 236,精簡后三角片個數為423。三角片數量明顯減少,而外形改變較小。
在虛擬加工平臺上,三角片精簡的效果以模型加載時間作為直接衡量標準。取平坦度加權方差閾值為0.1,改變精簡次數,建立加載時間與精簡次數關系如圖6所示。經過STL精簡算法導入,機床模型在虛擬加工平臺重的加載時間明顯減少。
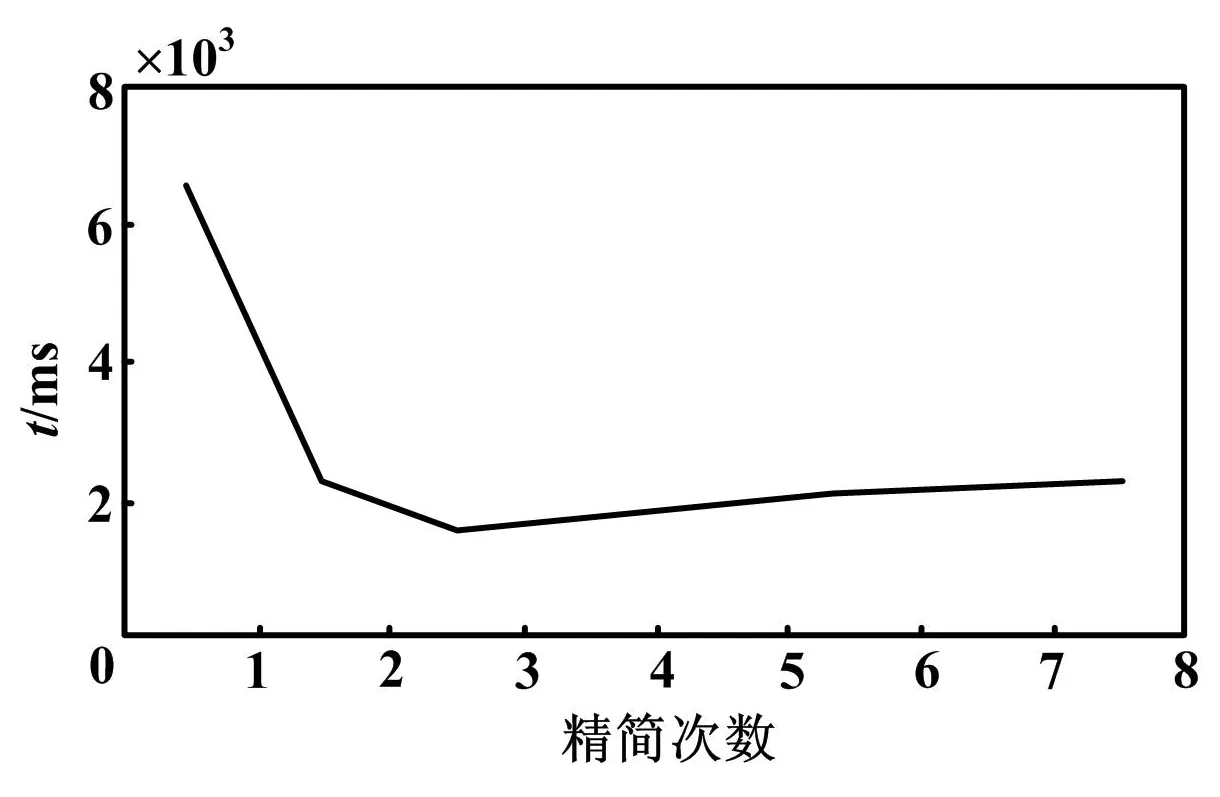
圖6 加載時間與精簡次數關系圖
虛擬加工系統仿真結果表明,采用均勻網格劃分的Z-Map模型的加工表面較為粗糙,而經過本文改進的Z-Map模型的加工表面較為光滑。本文提出的自適應Z-Map方法可以有效提升仿真的效果。由試驗結果可知,本文搭建的基于Android的虛擬加工仿真平臺可以清晰地反映虛擬加工仿真的全過程,驗證了基于Android環境開發的五軸數控加工仿真系統的可行性。
5 結束語
本文提出了一種基于模型優化的Android虛擬加工系統,將計算機仿真和虛擬加工引入到Android移動設備平臺,為虛擬加工仿真技術應用的研究提供了一個新的研究方向,有利于計算機虛擬仿真加工技術向更多應用方向發展。通過分析STL文件的文件結構,并對模型進行精簡,解決了STL數據量過大的問題,實現了機床在Android數控仿真系統的流暢加載與動態顯示。通過優化Z-Map模型的求交方法,使其能夠適用于五軸加工,并且提出了Z-Map自適應網格劃分方法。在加工過程中,實時優化Z-Map網格,提高了仿真效果。最后搭建了平臺上虛擬加工系統,驗證了虛擬加工在Android平臺上的可行性以及仿真效果。
[1]XIANGY,MALAKRC,LAUERC.Manufacturingsystemdesignwithvirtualfactorytools[J].InternationalJournalofComputerIntegratedManufacturing,2015,28 (1):25-40.
[2]DONGKL,YOUNGMINK.Studyonaprocess-centricmodelingmethodologyforvirtualmanufacturingofshipsandoffshorestructuresinshipyards[J].TheInternationalJournalofAdvancedManufacturingTechnology,2014,71(4):621-633.
[3]LEMUHG.Virtualengineeringindesignandmanufacturing[J].AdvancesinManufacturing,2014,2 (4):289-294.
[4]NOAKERPM.CAD/CAMcontrolsystemsandsoftware[J].ManufacturingEngineering,1996(3):222-240.
[5] 江本赤,郭利.STL模型簡化技術研究[J].機床與液壓,2009(8):231-250.
[6] 閆濤,姜曉峰.基于STL三角網格模型簡化的研究[J].計算機工程與設計,2010,31(23):5060-5074.
[7]SCHROEDERW,ZARGEJA.Decimationoftrianglemeshes[J].ComputerGraphic,1992,26(2):65-70.
[8]VOELCKERHB,HUNTWA.TheroleofsolidmodelinginmachineprocessmodelingandNCverification[C]//ProceedingsofSAE1981InternationalCongressandExposition,1981.
[9]HOOKV.RealtimeshadedNCmillingdisplay[J].ACMSIGGRAPHComuterGraphics,1986,20(4):15-20.
[10]HSUPL,YANGWT.Realtime3Dsimulationof3-aixsmillingusingisometricprojection[J].ComputerAidedDesign,1993,25(4):215-224.
[11]CHOIKB,CHUNGYC,PARKJW.ApplicationandextentionofZ-Mapmodel[C]//ProceedingsoftheThirdPacificGraphicsandAppliations,1995:363-382.
[12]王鵬遠.三軸數控銑削加工圖形仿真技術的研究與實現[D].蘇州:蘇州大學,2006.
[13]郝大功,閆光榮.Z-Map模型精簡技術研究[J].圖學學報,2007,28(1):134-138.
[14]神會存,周來水,賀美芳.基于頂點分類的曲面三角網格模型自適應光順研究[J].南京航空航天大學學報,2004,36(4):471-476.
Design of the Virtual Machining System Based on Model Optimization and Built on Android Platform
To solve the problems in implementing simulation of virtual machining on mobile platforms,i.e.,the excessive amount of data of model simulation,and the poor results of simulation,the STL simplified triangle model and optimizedZ-Map algorithm are proposed.The algorithms make it suitable for five-axis NC machining and improve the running efficiency of simulation program .In addition,theZ-Map mesh optimization method is given to ensure the running effect of the system on mobile platform.The virtual machining simulation system is built on Android platform; the experimental results verify the feasibility of the algorithm for combining Android platform with virtual machining,and the excellent simulation result.
Mobile platformSTL modelAndroid platformZ-Map algorithmComputer simulationVirtual manufactoryVirtual machiningFive-axis machining
褚人宇(1992—),男,現為上海大學機械制造及其自動化專業在讀碩士研究生;主要從事數控技術方向的研究。
TH-39;TP391
A
10.16086/j.cnki.issn 1000-0380.201609006
修改稿收到日期:2016-02-05。

