隨機風譜研究及其在海岸工程應用述評

左其華，杜齊魯，趙一晗，段子冰，王玉丹

(1.南京水利科學研究院，江蘇 南京 210029; 2.浙江大學 海洋學院，浙江 杭州 310058; 3.江蘇省水利規劃辦公室，江蘇 南京 210029)

隨機風譜研究及其在海岸工程應用述評

左其華1,2，杜齊魯1，趙一晗3，段子冰1，王玉丹1

(1.南京水利科學研究院，江蘇 南京 210029; 2.浙江大學 海洋學院，浙江 杭州 310058; 3.江蘇省水利規劃辦公室，江蘇 南京 210029)

作為海岸工程重要動力因素之一的風是隨機的，但在實際應用中大多仍作為恒定過程考慮。介紹了隨機風譜研究的基本狀況、理論基礎和常用的一些譜形式并進行適當地評述，對今后海岸工程隨機風譜研究及應用進行展望，可供海岸工程設計和研究參考。

隨機風譜；海岸工程；譜形式；風載荷；風速譜

Abstract:Wind,as an important factor of coastal dynamics,is also random and turbulent; however,it was normally designed as a constant variation with safety coefficient in coastal engineering.The development and theoretical basis of wind spectrum researches as well as the spectrum formulae published are reviewed in this paper; some comments are given,and the prospects of wind spectrum researches and applications are presented for future reference of the design and research in coastal engineering.

Keywords:random wind spectrum; coastal engineering; spectrum formulae; wind load; wind velocity spectrum

風紊動的隨機性早就被人們所認識，在陸地土木工程結構設計中比海洋工程中更早和更為深入。目前國際上許多組織都在做這方面的工作，如國際海洋學中心(NOC)，國際氣象協會(NMS)、全球氣象和聯合國教科文組織、美國氣象數據中心、英國氣象中心及全球波浪統計和北大西洋公約組織(NATO)。這些機構通常用儀器甚至目測的方法獲得大量不同時空尺度的現場數據。大量的科研人員基于一些假定進行了相當多的數值模擬。主要發達國家大都應用隨機風的概念規范各國土木工程結構的設計[1]。英國1988版的海工建筑物規范就指出“特別是目前已考慮將風譜法用于確定陣風所產生的風荷載”[2]。

我國于20世紀70年代以后，尤其是近二十年來做了大量隨機風的研究工作[3]，但這些工作主要在工業和民用建筑結構設計中較多，實驗室模擬才逐漸展開[4]。近年在跨海橋梁、沿海城市建設、風力發電等領域也開始應用隨機風概念。然而，大多海岸工程設計中，仍使用恒定風為動力，在港口工程技術規范[5]中只是以不均勻系數考慮其隨機影響。在考慮風對建筑物作用影響的實驗室試驗也多以均勻風為主。風的隨機性紊動對海岸工程中固定結構的穩定性、越浪量、泥沙運動、浮式結構動力響應等影響目前還很少被涉及。

根據當前海岸工程科學研究應用中尚很少涉及隨機風研究的現狀，本文主要對隨機風的基本研究狀況、理論基礎和國內外已有譜形式進行介紹和評述，以期為今后國內同類研究參考。

1 基本研究狀況

風能量可看作大量不同尺度渦旋的迭加，其發展階段可分為成長期、成熟期和衰減期。隨機風理論分析是在大氣層慣性力范圍內認為遵循Kolmogorov假定的基礎上進行的。脈動風速可用平穩隨機過程來表達，具有明顯各態歷經性，風的紊動是各向同性和均質的。這保證了在一定頻率或波數范圍內風運動過程有其一般的形式，如用高斯分布等描述。在此假定下，風在不同頻率上的能量分布可用譜來表達，由此而產生不同形式的譜。風的紊動是三維的，因此其譜也有三維特性，但人們為了簡化研究，往往只研究工程最關心的方向。當然，天然中的風，尤其是颶風，是非各向同性和非穩定的過程。

1948年，美國著名空氣動力學家von Karman提出了與高度無關的自由大氣層中的水平脈動風功率譜(von Karman譜)[6]。1959年，Panofsky等人提出了隨高度變化的垂直脈動風譜(Panofsky譜)[7]。1961年，加拿大著名風工程專家Davenport提出了第一個大氣邊界層中的水平脈動風功率譜(Davenport譜)[8]。1964年，Lumley和Panofsky對原Panofsky譜進行修正，提出新的垂直脈動風譜Lumley-Panofsky譜[9]。1970年Harris提出了其譜形式[10]，而后還得到其修正的譜[11]。1972年Kaimal也提出了一經驗譜，他是基于地面上5.66、11.3和22.6 m三個不同高度的風資料分析得到的，用其提出的表達式擬合目標函數得到了Kaimal譜[12]及其后來的改進形式[13]。1974年，美國學者Simiu提出了隨高度變化的水平脈動風譜(Simiu譜)[14]，該譜在我國一些規范中也有應有[15]。1977年挪威“Rules for the design construction and inspection of offshore structures”中提出的DNV譜在1988年修正為Harris-Det norske Veritas (Harris-DNV)譜[16]。1988年Ochi-Shin等提出了分段式模擬的風頻率譜[17]。一些機構也提出自己行業或國家海洋工程結構設計中推薦使用適合本區域的風譜，如美國石油研究所API譜[18]，歐洲使用的EUROCODE1譜[19]和挪威石油理事會提出的NPD譜[ 11]等。

由于風隨機作用對工程結構安全起到重大影響，近年來國外一些機構有系統地組織現場測驗和實驗室模擬。由美國佛羅里達大學商業和家庭安全研究所主持的the Florida Coastal Monitoring Program(FCMP)，1998-2005年間，進行了50次以上的觀測。對發生在美國不同地區(在Alabama，Florida，Louisiana，Mississippi，North Carolina和Texas等州(市))20多場重要的臺風進行分析，基于每一樣本15分鐘的時間過程，分析了平均風速U及其方向，以及三個紊動強度分量(u，v，w)，還得到三個協相關uw，uv，vw及最大3 s陣風相關特征要素。2010年Masters等人[20]進行了2005年三場大西洋臺風(Katrina，Rita和Wilma)過程在表面層的實驗，將9個移動儀器放在海岸地區靠近三個臺風預期的路徑上，在地面上5 m和10 m二個不同高度處測量風的平均和紊動特性。觀測到10 m高度上的15 s平均風速最大值在23.0～36.0 m/s之間變化，而60 s平均風速的最大風速值則在29.2～41.9 m/s之間變化。Balderrama等人[21]基于1999-2008年大西洋颶風季節臺風現場觀察對陣風極值進行特征分析，對19場風暴的64個相關測站記錄進行組合和質量控制，得到一個大的數據庫。

我國風紊動研究在土木工程中的應用主要在房屋和工業建筑或橋梁設計中。最早在相關行業規范中應用的是西安熱工研究所的規范譜[22]。近年隨著沿海大橋和風電開發等工程建設相繼開展了一些現場觀測，中國大陸和港、臺也取得了顯著成績，但模擬的譜基本是以國外已有的譜為靶譜。顏大椿等[23]研究了在虎門懸索橋西塔架一側的金鎖牌燈塔頂部設置觀察站(標高28.5 m)測得的資料，進行水平脈動速度功率譜擬合，認為在峰值頻率為0.02時平均功率譜略低于Kaimal譜。Bao-Shi Shiaua等人[24-25]研究了基隆海岸1998年10月25～27日強臺風BASE的風紊動特性統計及其縱向和垂向風速譜。用的是超聲波測風儀，采樣頻率為20 Hz。研究認為：1)縱向和垂向紊動強度之比是1∶0.46；2)風速分量的概率密度函數符合高斯分布；3)觀測得到的橫向和垂向風譜與Von Karma譜方程和歐洲規范化的各向同性的紊動譜方程相近。Xu等人[26]在高約384 m的深圳帝王大廈塔頂設站觀測得到1996年的臺風Sally過程資料，分析的數據是1小時平均，而不是10分鐘平均，風速譜密度值是整個25小時的，得到集合長度尺寸為255 m，平均紊動強度是11.5%，相應的平均風速是12.2 m/s。安毅等[27]研究了2011年Muifa臺風正則化的縱向譜，資料是在上海國際金融中心492 m的頂上測得的，安裝有2個超聲風速儀，詳細提供了風速、紊動強度和紊動譜，用的是10分鐘平均值，譜的平均風速是30.3 m/s。觀測到的正向集合長度尺寸是217.6 m，然而不知此值是否是在平均風速條件下得到的。王浩等[28]用基于蘇通大橋橋址區三次強風(臺風鳳凰、海鷗及冬季強北風) 實測數據，順風向脈動風譜參考Kaimal譜、豎向目標譜參考Panofsky譜來擬合。胡曉紅等[29]用上海“派比安"臺風實測結果擬合二維脈動風譜，水平方向風速(U，V)分別以Von Karman譜、Davenport譜和simiu譜為目標譜，垂直方向(W)分別以Panofsky譜和Lummley-Panofsky譜為目標譜。Li等[30]研究了Hagupi臺風在南海的風譜，觀測站設在Zhizai島上。島長120 m，寬50 m，海拔11 m。與陸地最短的直線距離是4.5 km，與Dazhuzhou島(離岸四海里)距離約1 km。測點距地面100 m高。在W-N-NE方向和E-SE方向是開敞的。在地面上7個不同高度架設觀測儀器，分別為8、10、20、40、60、80和100 m，將臺風路徑分成風眼、眼-壁區和外圍渦旋三個區域。選擇代表性樣本的原則是：(a)平均風向：平均風速大于17.2 m/s的10 min平均風向；(b)平均風速：10 min平均風速大于17.5 m/s；(c)方向包括22.5°范圍。將譜分為不同情況來估計：鋒渦旋區外(FOV)、風眼-壁區(FEW)、后眼-壁區(BEW)和后渦旋區外(BOV)。結果表明，眼-壁區域風速最大。

2 風譜基本理論[3,30,31]

紊動速度脈動中每一渦旋是以圓頻率或以波數k作周期運動的，因此，紊流運動的總能量可以認為是氣流中每一渦旋貢獻的總和。用函數E(k)定義為渦旋運動的能量譜，表示能量貢獻與波長(數)的關系。影響能量耗散的主要是那些小的渦，其剪切變形及黏性應力比較大。當沒有能量來源時，紊流運動的動能將逐漸減小。黏性作用越大，衰減越快。反之亦然。

對于黏性作用較弱的情況，在大波數區間，衰減時間比渦旋的周期長，可以近似認為大波數區，渦的能量是定常的，大渦通過慣性傳遞輸送給這些渦的能量被黏性作用耗散的能量抵消，于是小渦的運動由能量傳遞率和黏性系數來確定。這就是Kolmogrove第一假說。由這一假說可以得出，小渦運動與邊界等外部條件無關，它是局部各向同性的，即小渦的運動沒有特定的方向。如果進一步假設，能量耗散幾乎全部由氣流中那些最小的渦產生，那么在Kolmogrove第一假說成立的大波數區中，黏性影響很小，在這個范圍內可假設渦的運動與黏性無關，因此它可完全由能量耗散率來確定，這個假設稱為Kolmogrove第二假說。

紊動譜可分為三個主要頻率區域：1)大量紊動能量產生區域；2)慣性子域，此處能量既不產生也不消失，但是向小尺寸方向傳輸；3)能量消失區域。遵循 Kolmogorov假定和量綱分析，慣性區域的譜S可表示為：

式中：au是常數，在中性層時，au≈0.5；ε是能量傳遞率；K是波數。

根據Kolmogrove理論，頻域內的脈動風功率譜S寫成：

式中：n為頻率,u*表示摩阻速度，f為相似律坐標或莫寧(Molin)坐標，A和B是二個常數。也可寫成其一般形式：

式中：U是平均風速(m/s)，R是標準差σu和摩阻速度之比，即：

式中：Λ是幾何尺寸，可認為是離開地面高度z或某一高度的集合尺度L或整個高度上的常數長度。當Λ取離開地面高度z時，則

當Λ取集合尺度L時，其形式為：

Monin-Obukhov理論表明，大氣穩定度對自然風的湍流特性具有重要影響，在大氣近地層高度內，湍流特性可由相似性理論得到的大氣穩定度參數確定：

式中：κ為馮卡門常數，q為垂直熱量通量，ω和T'為垂直脈動速度和脈動溫度，ρa、T0分別為大氣平均密度和溫度，g為重力加速度，Cp為定壓比熱；工程中，由于集合尺度確定不很方便，大多取式(5)作為莫寧坐標。

風速在高度上變化可由對數律公式給出：

式中：z0為地面粗糙度。不考慮ψ(ζ)影響時，可簡化為常用的風速對數律公式。

對于中性的大氣，z/L趨于0；對穩定的大氣，z/L大于0；不穩定條件下z/L小于0。嚴格來講，中性層狀并不存在，但近似中性層流的z/L趨于0，可認為是中性的。

式(1)中能量在表面層傳遞的速率可表示為：

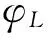
從理論上講，式(3)可以滿足下列要求：

1) 慣性區域，與式(10)協調，則

αβ-γ=2/3

2) 當頻率N趨于0，譜可滿足下列條件

得：γ=1,A=4Cβ。

α≥1

目前大多譜是以式(3)的形式用實測資料進行擬合的。

3 風速譜形式

20世紀40年代以來，國內外學者根據強風記錄進行相關分析或曲線擬合，發表了各種紊動風速譜公式。

3.1國外有關風速譜

3.1.1 水平脈動譜

1) von Karman譜[6]

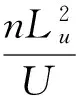
式中：?=ω為圓頻率；u、v、w為x、y、z向的脈動風速；Lu、Lv、Lw分別為橫向、縱向、垂向湍流集合尺度，其中常數a=1.339。

2) Davenport譜[8]

式中：U10為地面高度上10 m的平均風速。

這是大氣邊界層水平脈動風譜的近似表達式，也是目前國際上用得最早也可能是最多的水平脈動風譜。或可寫成：

式中：C是粗糙度系數，在0.001 5～0.003間。風下邊界愈粗糙，值愈大。或：

式中：x0=1 200n/U10，U10為10 m 高度處的平均風速(m/s)；K為表面阻力系數。Davenport 譜具有參數簡單、不隨高度變化、便于工程應用等特點。其表達式中僅有一個系數K，不過K的實測值非常分散，難以準確確定。

3) Harris譜[10]

其修正的譜形式為

式中：u1h為1小時平均風速值。對于粗糙海面，C取0.002；對于中等海況，C取0.001 5。

4)Simiu譜[14]

5)Kaimal譜

6)Ochi-Sjin譜

C=(750+69U10)×10-6

7)Harris-Det norske Veritas譜[16]

式中：系數C與Harris譜相同。

8)API譜

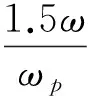
式中：ωp=2πFp=2π0.025V(1h，z)/z或=2π×0.025V(z)/z；ωp,Fp分別為峰值圓頻率或頻率，z取海面標準高度20 m。

σ(z)=0.15V(z)(z/za)-0.125

或Fp=0.025V(1h，z)/z=0.025V(z)/z；

9)Eurocode1譜

10)NPD譜

f=172n(U10/10)2/3(z/10)-0.75，N=0.468

式中：U10為1小時平均風速。

3.1.2 垂直脈動風譜

1)Pamfsky譜

2)Lumley-Panofsky譜[9]

3.2我國有關風速譜

1) 西安熱工所譜

該譜雖目前我國相關規范已很少用，但此譜是我國最早的風速譜，在此一并列出。

2) 虎門懸索橋臺風譜

順向風譜：

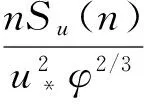
垂向風譜：

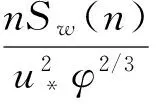
式中：φ為大氣穩定參數。

3) 基隆海岸風速譜

順向風譜：

垂向風譜：

4) 蘇通大橋譜

順風向脈動風譜(參考Kaimal 譜)：

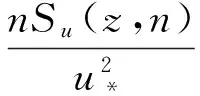
豎向目標譜(參考Panofsky 譜)：

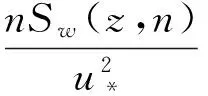
5) 上海“派比安"臺風譜

水平向脈動風譜擬合：

① 擬合Von Karman譜

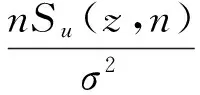
② 擬合Davenport譜

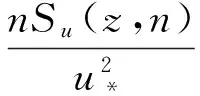
③ 擬合Simiu譜

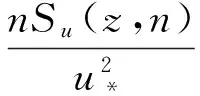
垂直向脈動風譜擬合：

① 擬合Panofsky譜

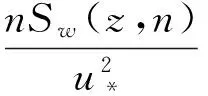
② 擬合Lummley-Panofsky譜)

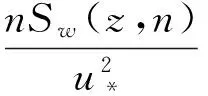
6) 南海Zhizai譜(Hagupi臺風)

4 譜的比較和分析

國內外已有的主要譜公式可以分為三類：一類是在頻率n為0時，譜密度值為0(如Davenport譜)，這類譜因其直觀，與其他研究方向的譜形式相近，一些參數也較易確定，雖然由陸地資料得到，但在其他工程中，甚至在一些海岸工程中也有應用；第二類是在頻率n為0時，譜密度值不為0，但譜密度最大值不是發生在最低頻處，而是由低頻逐步增大乃至達到峰值，然后逐漸下降。這類譜形式目前數量最多，在工程應用中也最廣泛；第三類譜是其密度最大值發生在頻率n為0或最低頻率處。這類譜主要用于一些深海工程。我國西安熱工所譜在頻率n為0時，有奇點。

圖1列出了第一、二類譜各種不同公式譜的比較[17]，我國近年所采用的經驗譜均是以這類譜為目標譜進行擬合得到的。這類譜大多用于陸地工程，如房屋、工業、橋梁等土木結構設計中，因為這些結構中桿件的自振頻率往往與高頻有關。這類譜的理論依據為式(3)，表1列出了各譜與式(3)比較后所得的各系數，“譜名”列括號中的值為上節對應各式的譜，行中所對應的各參數是式(3)中的變量，其中R項已根據其定義移至式左。盡管式(3)左式分母中的速度表示形式可能略異，但總體來講，各式只是式中系數量值的差別。這些系數的差別可能主要來自不同樣本的差異，如樣本間資料量測站點所處的周圍環境、測點高度和采樣時距及延時等不同。我國在南海實測的Zhizai譜還表明在同一測點這些系數還與所處的不同時刻的臺風過程有關。這些也表明盡管脈動風功率譜的形式多種多樣，但適合于某一特定地區地理環境的功率譜，甚至于某個強風的功率譜并不一定就可以用這些已有的譜來表示。因此，根據某一地區的實測風速數據擬合出一條適合該地區的脈動風速功率譜尤其確定其中合適的參數具有重要意義。

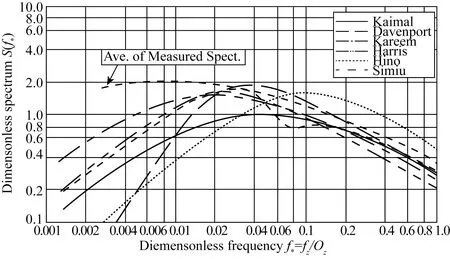
圖1 第一、二類譜不同形式比較Fig.1 Comparison of some dimensionless spectrum densities in frequencies

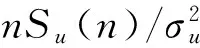
表1 一些主要譜與公式(3)比較Tab.1 Comparison of some spectrum coefficients with Eq.(3)

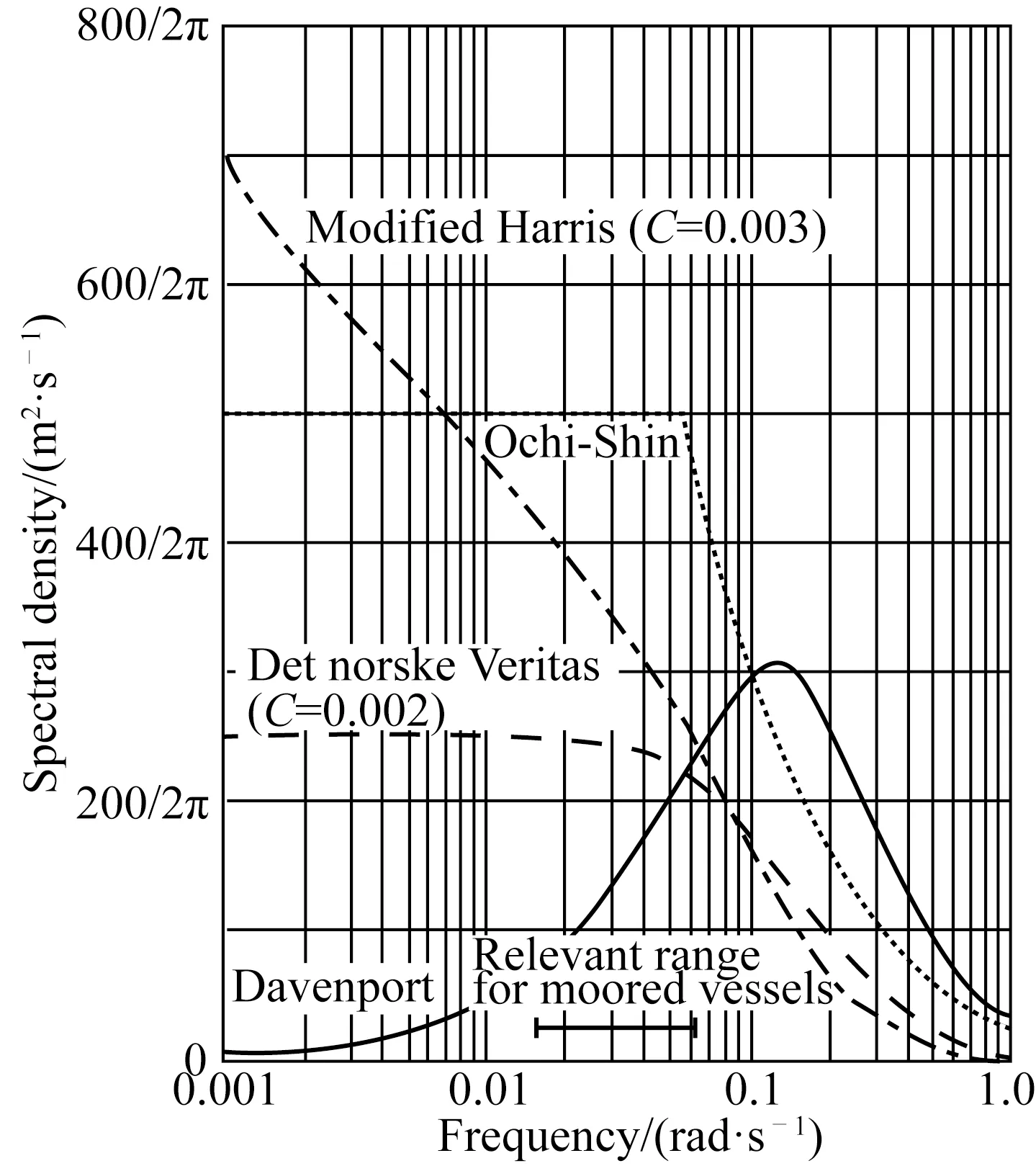
圖2 第三類譜型比較(U=30.9 m/s)Fig.2 Comparison of the third kind of wind velocity spectrums

圖2給出了幾個典型第三類譜在特定參數條件下(U=30.9 m/s)的譜形(也包括了Davenport譜)比較[11]。各譜差異明顯大于第二類譜，尤其在低頻處的值差異更大。這些差異主要可能是譜大都用于深海或離岸結構物的設計，各海區或結構物等級等原因。由于該類譜在低頻部分有較多的能量，而海洋工程中浮式或一些錨系結構對低頻的響應較為敏感，所以海洋工程結構研究大多采用這一類譜。

式中：u(t)是隨機的紊動風速部分。圖3也表明在(x,y,z)三個方向的風速譜都存在這一趨勢[24]。

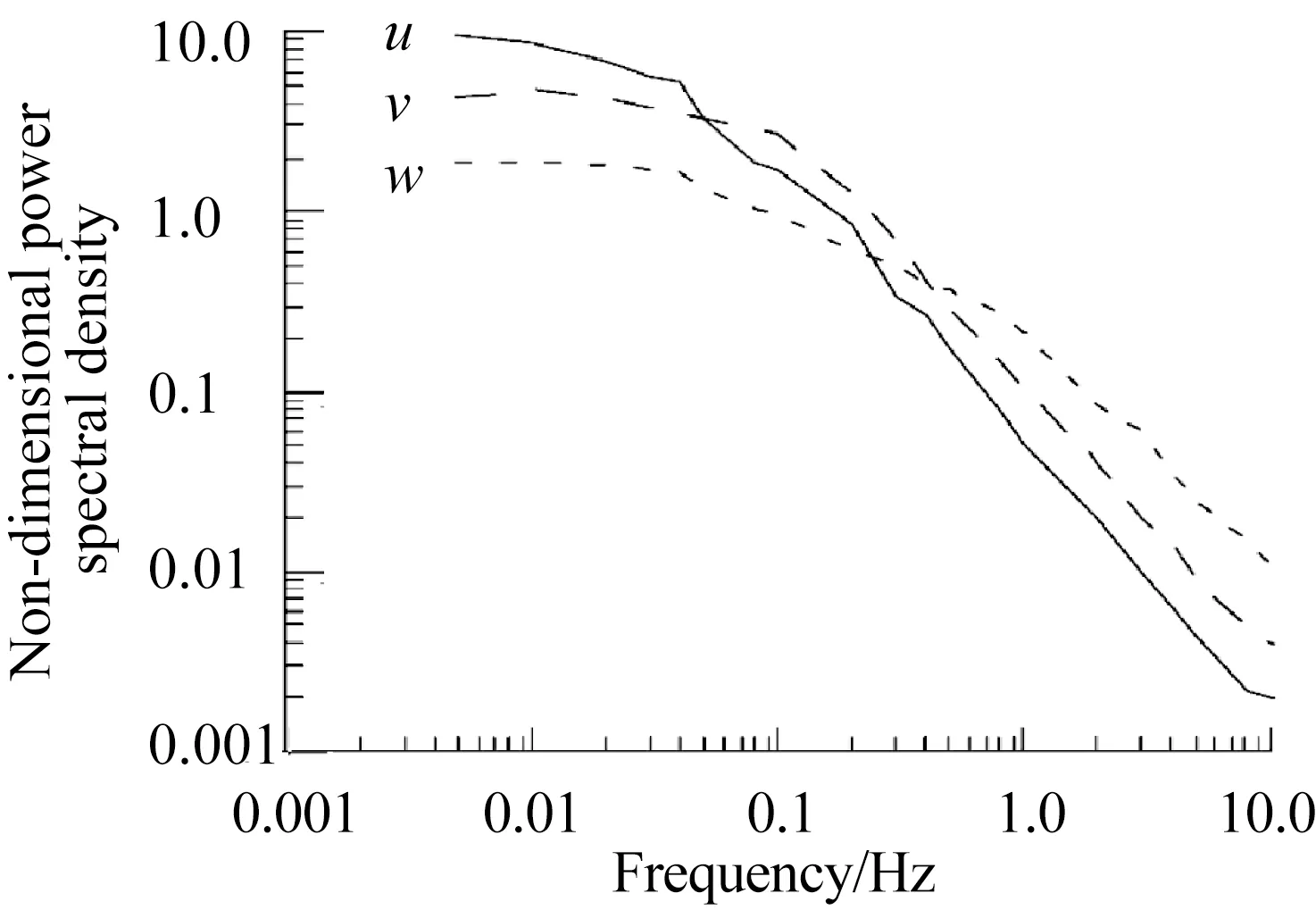
圖3 低頻風譜趨勢比較Fig.3 Trend comparison of low frequency wind spectrums at different directions (x,y,z)

NPD譜的基本譜形與API譜相同，但在低頻部分NPD上升速率更快些。圖4給出了二譜的比較。API-RP 2SK-2005[32]認為使用NPD譜時，在陣風周期大于500 s時，對風譜的描述有很大不確定性，建議在海洋工程浮體結構共振周期大于500 s時，宜用API譜上界的風譜(α=0.01)。

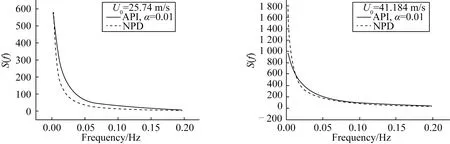
圖4 NPD風譜和API風譜的比較*浮式平臺總體性能[R].哈爾濱工程大學，深海工程技術中心，2013.Fig.4 Comparison of NPD spectrum with API spectrum

綜上所述，第一、二類譜主要適用于那些對高頻敏感的結構物，尤其在陸地結構物設計中多為應用。這二類譜大多基于經典的隨機風理論得到。第三類譜主要應用于深水結構，尤其是浮式結構，這些結構的響應都與低頻振動密切相關，大多依據工程應用需要確保工程結構安全得到。

5 結語和展望

5.1結語

1)基于Kolmogrove假說，認為風是由各向同性和處于中性層的條件下建立起來的風譜理論，經幾十年的不斷改進，已相對成熟，并由此產生了一系列與之適應的風譜形式。

2)已有的風譜可以歸為三種不同的種類，大多基于理論模型并用實際臺風進行參數模擬得到。不同種類的譜適用于不同類型的工程結構設計。峰值頻率在高頻處的譜主要適用于陸地或小尺寸結構設計，而深海具有低頻共振周期的浮式和錨系等結構振動設計主要用第三類風速譜。適用于海岸工程的風速譜形式尚不十分清晰。

3)中國自20世紀90年代以來，已在沿海進行了一定數量的現場隨機風的測量和風速譜的分析，為跨海跨河橋梁等工程結構設計起到重要參考作用，但對隨機風的系統研究尚未形成，或僅就實際工程進行專題研究，其譜形式也大都是參考國外已有形式進行擬合。

5.2展望

1)在理論方面要加強非平衡和各向異性的隨機風過程研究。自然中的風真正處于中性層的并不多，尤其在強風過程中更是這樣。臺風各階段甚至同一階段不同區域的紊動變化也是劇烈的。顯然，目前的研究對如何描述這一現象尚不完善。

2)已有很多譜的形式存在，但究竟用何種特征風速來進行研究尚未形成統一的意見，如3 s、1 min、3 min、5 min、10 min、15 min、1 h等。這事實上也導致各譜較難進行比較。已有的研究表明，不同特征風速會造成譜值甚至譜形式的差異。一般來講，特征風速確定所取時段愈長，其平均風速值愈小，但也有與之相反的例子。因此，仍需積累大量資料，采用更為科學的量測儀器或更多的數值模擬方法，研究如何規范特征風速及其對工程安全的影響。

3)現行的譜分析和研究仍大都基于付里葉變換的正反演技術得到。已有文章認為，傳統譜分析方法已經過時[33]，應采用小波變換等新方法。筆者認為，對特定隨機風(及浪)過程應用小波變換方法可以得到更多的紊動信息，但在反演應用方面，傳統的方法或更具有靈活性，更符合隨機過程不確定性特點。小波變換所得譜的反演技術困難是可克服的，但其結果可能僅是其分析所得的某一特定過程。

4)雖然在陸地、深海的風譜形式已有不少成果，在海岸現場觀測中也建立了一些特定的擬合譜形式，但在如何選擇適用于海岸工程設計的風譜方面，仍需進行更多研究。我國沿海岸線長，各地區海岸地理和自然條件跨度大，差異也大，當前要加強沿海強風過程資料積累。在常規長期資料監測方面，傳統風杯式測量儀器應得到改善，以便能得到實時強風過程及適用于不同海岸區域的風速譜。

5)應進行隨機風概念在海岸工程得到應用對傳統的科學研究和設計方法帶來影響的研究。在海岸動力方面，隨機風與隨機波浪和潮流應以何種方式組合？對沿岸環流會有何種影響？在結構物響應方面，對防波堤和護岸結構穩定和越浪量的影響?對碼頭靠泊等浮式結構的影響？對海岸工程中小尺寸結構荷載的影響？各種不同類型的結構設計如何選用不同類型的風速譜？隨機風也有群性？風與浪二種隨機動力聯合作用的群性問題？海岸工程設計中可能會遇到高頻和低頻風影響同時存在顯著影響問題。

6)在空氣動力學研究方面，已進行了不少隨機風的實驗室大(全)尺度實驗的研究，但在海岸工程研究中還很少。首先應解決隨機風模擬的造風系統，當前主要是風泵的動力響應問題。如采用恒定風，但在出風口處進行隨機風的處理，應解決出風口風速沿垂向的變化從而影響水波傳播的問題。進行風-流體-結構相互作用研究時，會遇到雷諾相似和佛汝德或柯西相似的限制導致時間比尺不協調等問題。

7)與海岸工程設計和研究相應的風作用技術規范的修訂。

[1] KWON D K,KAREEM A.Comparative study of major international wind codes and standards for winds effects on tall building[J].Engineering Structures,2013,51:23-35.

[2] BS6349.英國標準規范——海工建筑物[S].全國水運工程標準委員會,1990.(BS6349.British standard coded of practice for maritime structure[S].1990.(in Chinese))

[3] 張相庭.結構風壓和風振計算[M].上海:同濟大學出版社,1985.(ZHANG Xiangting.Structural wind pressure and wind induced vibration calculation[M].Shanghai:Tongji University Press,1985.(in Chinese))

[4] 張云彩,姚美旺.海洋工程水池試驗中風速譜的模擬[J].中國海洋平臺,1994,(Z1):175-179.(ZHANG Yuncai,YAO Meiwang.Simulation of the velocity spectrum of the stroke in the marine engineering pool[J].China Offshore Platform,1994,(Z1):175-179.(in Chinese))

[5] JTJ215-98.港口工程荷載規范[S].中華人民共和國交通部,1998.(JTJ215-98.Load code for port engineering[S].1998.(in Chinese))

[6] VON Kármán Tv.Progress in the statistical theory of turbulence[J].Proceedings of the National Academy of Sciences,1948,34(11):530-539.

[7] PANOFSKY H A,MCCORMICK R A.The spectrum of vertical velocity near the surface[J].Quart.J.Royal Meteorological Society,1960,86(370):495-503.

[8] DAVENPORT A G.The spectrum of horizontal gustiness near the ground in high winds[J].Quart.J.Royal Meteorological Society,1961,87(372):194-211.

[9] LUMLEY J L,PANOFSKY H A.The structure of atmospheric turbulence[M].New York:John Wiley & Sons,Inc.,1964.

[10] HARRIS R I.The structure of the wind,Semin.Mod.Des.[C]//Wind-Sensitive,Struct.,Construct.Ind.Res.Inf.Assoc..1970:29-55.

[11] FEIKEMA G J,WICHERS J E.The effect of wind spectral on the low-frequency motions of a moored ranker in survival condition[C]//Proceedings of the 23rd Annual Offshore Technology Conference.Houston,1991:OTC6605.

[12] KAIMAL J C,WYNGAARD J,IZUMI Y,et al.Spectral characteristics of surface layer turbulence[J].Quart.J.Roy.Meto.Soc.,1972,98(417):563-589.

[13] KAIMAL J C.Horizontal velocity spectra in an unstable surface layer[J].J.Atmos.Sci.,1978,35(1):18-24.

[14] SIMIU E.Wind spectra and dynamic along wind response [J].Journal of the Structural Division,ASCE,1974,100(9):1897-1910.

[15] JTG/TD60-01-2004.公路橋梁抗風設計規范[S].北京:人民交通出版社,2004.(JTG/TD60-01-2004.Wind resistant design specification for highway bridges[S].Beijing:People's Communications Press,2004.(in Chinese))

[16] FORRISTALL G Z.Wind spectra and gust factor over water[C]//Proceedings of the 20th Offshore Technology Conference.Houston,1988:OTC5735.

[17] OCHI M K,SHIN Y S.Wind turbulent spectra for design consideration of offshore structure[C]//Proceedings of the 20th Offshore Technology Conference.Houston,1988:OTC5736.

[18] RP2A-WSD,Planning,designing,and constructing fixed offshore platforms-working stress design[S].Houston:American Petroleum Institute,2002.

[19] European Committee for Standardization (CEN).Eurocode 1:Actions on structures-Part 1-4:General actions-wind actions[S].EN 1991-1-4:2005/ AC:2010 (E).

[20] MASTERS F J,TIELEMAN H W,BALDERRAMA J A.Surface wind measurements in three Gulf Coast hurricanes of 2005[J].J.Wind Eng.Ind.Aerodynamics,2010,98(10):533-547.

[21] BALDERRAMA J A,MASTERS F J,GURLEY K R.Peak factor estimation in hurricane surface winds[J].Wind Eng.Ind.Aerodynamics,2012,102:1-13.

[22] 楊應華,魏俊，馮真.風速譜對大跨度屋蓋風振系數的影響[J].特種結構,2010,27(6):29-33.(YANG Yinghua,WEI Jun,FENG Zhen.Influence of wind speed spectrum on wind vibration coefficient of long span roof[J].Special Structures,2010,27(6):29-33.(in Chinese))

[23] 顏大椿,干輝,羅熾濤,等.虎門懸索橋址的臺風譜測量[J].工程力學,1999(S2):61-67.(YAN Dachun,GAN Hui,LUO Zhitao,et al.Typhoon spectrum measurement of Humen suspension bridge[J].Engineering Mechanics,1999(S2):61-67.(in Chinese))

[24] SHIAU B S.Velocity spectra and turbulence statistics at the northeastern coast of Taiwan under high-wind conditions[J].Journal of Wind Engineering and Industrial Aerodynamics,2000,88(2):139-151.

[25] SHIAU B S,CHEN Y B.In situ measurement of strong wind velocity spectra and wind characteristics at Keelung coastal area of Taiwan[J].Atmospheric Research,2001,57(3):171-185.

[26] XU Y L,ZHAN S.Field measurements of Di Wang Tower during Typhoon York[J].Journal of Wind Engineering and Industrial Aerodynamics,2001,89 (1):73-93.

[27] 安毅,全涌,顧明.上海陸家嘴地區近500 m高空臺風“梅花”脈動風幅值特性研究[J].土木工程學報,2013,46(7):21-27.(AN Yi,QUAN Yong,GU Ming.Turbulence characteristics analysis of typhoon ‘Muifa’ near 500 m above ground in Lujiazui district of Shanghai[J].China Civil Engineering Journal,2013,46(7):21-27.(in Chinese))

[28] 王浩,鄧穩平,焦常科,等.蘇通大橋鳳凰臺風現場實測分析[J].振動工程學報,2011,24(1):36-40.(WANG Hao,DENG Wenping,JIAO Changke,et al.Field measurements on typhoon Fung-Wong at the Sutong Bridge[J].Journal of Vibration Engineering,2011,24(1):36-40.(in Chinese))

[29] 胡曉紅,葛耀君,龐加斌.上海“派比安”臺風實測結果的二維脈動風譜擬合[J].結構工程師,2012(2):41-48.(HU Xiaohong,GE Yaojun,PANG Jiabin.The fitting of 2D fluctuating wind spectrum for the actual measurement data of “pba” typhoon in Shanghai[J].Structural Engineers,2012(2):41-48.(in Chinese))

[30] LI L X,XIAO Y,KAREEM A,et al.Modeling typhoon wind power spectra near sea surface based on measurements in the South China sea[J].J.Wind Eng.Ind.Aerodyn,2012,104:565-576.

[31] HAN T,MCCANN G,MüCKE T A,et al.How can a wind turbine survive in optical cyclone? [J].Renewable Energy,2014,70(50):3-10.

[32] API RP 2SK-2005.Recommended practice for design and analysis of station keeping system for floating structure[S].American Petroleum Institute,2005-10-01.

[33] LIU P C.Is the wind wave frequency spectrum outdated[J].Ocean Engineering,2000,27(5):577-588.

Review of studies on random wind spectrum and its application in coastal engineering

ZUO Qihua1,2,DU Qilu1,ZHAO Yihan3,DUAN Zibing1,WANG Yudan1

(1.Nanjing Hydraulic Research Institute,Nanjing 210029,China; 2.College of Ocean,Zhejiang University,Hangzhou 310058,China; 3.Water Resources Department of Jiangsu Province,Nanjing 210029,China)

TV148

A

10.16483/j.issn.1005-9865.2016.02.015

1005-9865(2016)02-0111-12

2015-09-30

水利部公益性行業科研專項資助項目(20141004)

左其華(1954-)，男，博士，教授級高級工程師，主要從事海岸工程研究。E-mail：qhzuo@nhri.cn