元素最小描述并集下的概率粗糙集模型及其決策
蔡克參*,劉財輝
?
元素最小描述并集下的概率粗糙集模型及其決策
蔡克參*,劉財輝
(贛南師范大學數學與計算機科學學院,江西贛州,341000)
基于元素的最小描述并集,本文提出了一種新的概率粗糙集模型。針對新模型設計了相應算法來計算元素最小描述并集及相應條件概率。最后通過一個實例,比較了已有模型和新模型在決策中的應用,結果表明新模型更具有合理性。
粗糙集;覆蓋;最小描述;概率粗糙集;決策粗糙集
引言
粗糙集理論[1]是Pawlak于1982年提出的一種新的處理模糊和不確定性知識的數學工具。隨著粗糙集理論研究的不斷深入,粗糙集的研究領域不斷被拓寬。目前人們研究較多的粗糙集模型有:覆蓋粗糙集、概率粗糙集、決策粗糙集、多粒度粗糙集等。覆蓋粗糙集的概念是Bonikowski[2]從實際應用出發利用論域上的覆蓋關系對粗糙集進行推廣,與覆蓋粗糙集結合的研究內容很廣泛,文獻[3]研究了覆蓋粗糙集與決策模型之間的結合運用。許多學者對覆蓋粗糙集中的最大、最小描述概念在粗糙集進行了研究。文獻[4]用矩陣的方法對最大、最小描述進行了計算,文獻[5-6]在覆蓋廣義粗糙集理論中,對最小描述的定義進行了討論,集合并拓展了多粒度覆蓋粗糙集模型;文獻[7]給出了基于最小描述交的覆蓋近似算子,豐富了覆蓋粗糙集理論;文獻[8]研究了最小描述與模糊集中隸屬度的關系,建立了一個新的覆蓋粗糙集模型。概率粗糙集[9]是Pawlak粗糙集模型的一種推廣形式,經典的概率粗糙集模型是基于等價關系建立的,文獻[10-11]提出了新的概率粗糙集模型,文獻[12-13]對不同模型下的概率粗糙集模型算法進行了分析。決策粗糙集模型是Yao等人[14]1990年提出的,文獻[15-17]對原有的概率粗糙集模型進行了拓廣,提出了幾種新的決策粗糙集模型,文獻[18-19]很好的融合了粗糙集理論和決策理論,方便了實際的決策運用,文獻[20]總述了決策粗糙集的研究現狀。
一般情況下基于等價關系的粗糙集模型,往往受限較多,在決策中往往決策結果也不太理想。針對這一問題,已經有學者建立了基于覆蓋關系的概率粗糙集模型,討論了元素最小描述交集在概率粗糙集模型中的決策及運用。受此啟發,本文將覆蓋粗糙集中最小描述與概率粗糙集、決策粗糙集相結合,提出了一種元素最小描述并集下的決策粗糙集模型。該模型對原有的概率粗糙集模型進行了拓展,并結合具體的實例進行了新模型合理性的說明。
1 基本概念
定義1[21]給定一個覆蓋近似空間,其中是論域,是的一個覆蓋。對任意的,稱

定義2[9]設是非空有限論域,集函數稱為概率測度,若:

定義3[9]設是有限論域,是上的概率測度,,稱為事件發生條件下事件發生的條件概率。
定義 4[9]給定非空有限子集,為論域上的等價關系。論域上的一個劃分。對,Pawlak粗糙集的正域,邊界域和負域,其定義分別為:

(4)
這樣,就得到了Pawlak三個域的另一種表示:

定義 5[9]對,令,則概率粗糙集的-正域、負域和邊界域可定義為:
(6)
2 元素最小描述并集下的概率粗糙集模型
本節主要結合以上所給定義,對概率粗糙集模型進行拓展,給出了基于元素最小描述并的概率粗糙集模型,并對其性質及求解過程進行了分析。
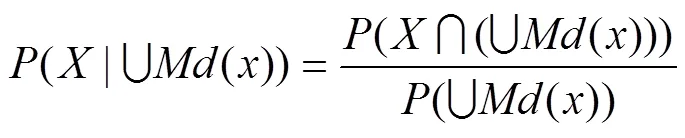
為元素最小描述并集下的條件概率。
下面結合算法對所給定義進行分析說明。設計算法使用了JAVA語言,程序運行環境是myeclipse 8.5,限于文章篇幅,下面只給出算法的主要思想及核心部分的代碼。
2.1 計算元素最小描述并集算法設計
該算法的主要運用兩個嵌套的for循環,找出同時包含某個共同元素的集合,比較集合間的包含關系,取被包含的集合作為輸出對象,循環輸出結果,求出元素最小描述。再求出每個元素對應的最小描述集合內所有元素的并集;核心代碼如下:
//求元素最小描述
for (String variable : variaList){
List
for (int i = 0; i < variaCollections.size();i++){
Set
if (variaCollection.contains(variable)){ variaReflectCollection.add(variaCollection);
for (int j = 0; j < variaCollections.size() ;j++){
if (j != i) { Set
if (variaCollection.containsAll(chirldVariaCollection) && chirldVariaCollection.contains(variable)){
variaReflectCollection.remove(variaCollection);
}}}}}
variaIncludedRelationships.put(variable, variaReflectCollection);
}
return variaIncludedRelationships;
//最小描述內部元素取并集
public static Map
Map
for (Map.Entry
List
Set
System.out.println("元素" + entry.getKey() + " 對應的最小描述: " + entry.getValue() + " 對應的自并集合為: " + intersection); intersections.put( entry.getKey(),intersection);
}
return intersections;
}
2.2 元素最小描述并集下的條件概率算法設計
本算法的設計調用了上面的最小描述并集算法,主要分以下幾個步驟進行:
步驟1 調用intersection()集合求交集函數,求出給定集合與最小描述并集中集合的相交集合;
步驟2 取步驟1所得集合與最小描述并集合元素個數的比值;
步驟3 使用System.out.println輸出條件概率。
主要部分代碼如下:
//取并集后的集合與給定集合取交集
String[ ] pointArray = {"x1","x2","x3","x4"};
Set
public static Set
Set
intersectionSet.clear();
for (int i = 0; i < variaCollections.size();i++){
Set
if (i == 0) intersectionSet.addAll(variaCollection);
else
intersectionSet.retainAll(variaCollection);
}
return intersectionSet;
}
//求兩個集合元素個數的比值
public static Set
Set
intersectionSet.clear();
intersectionSet.addAll(set1);
intersectionSet.retainAll(set2);
return intersectionSet;
}
public static String probability(Set
Set
return set1.size()+"/"+set2.size();
}
//輸出各元素對應的概率
System.out.println("元素" + entry.getKey() + " 對應的最小描述: " + entry.getValue() + " 的條件概率為:" + probability);
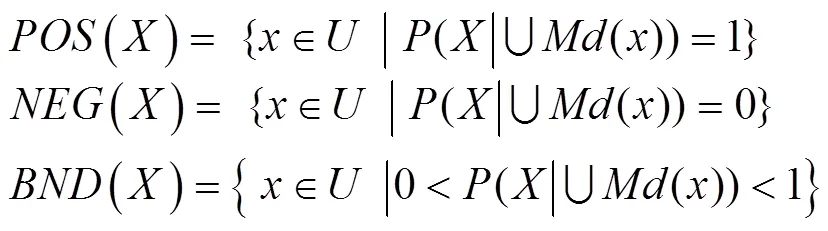
(9)
3 兩種概率粗糙集模型下的決策情形
本節主要使用上一節提出的基于元素最小描述并集的概率粗糙集模型,并結合一般的基于等價關系建立的概率粗糙集模型,對Pawlak粗糙集、0.5-概率粗糙集和概率粗糙集共三種粗糙集模型進行決策。比較以上兩種概率粗糙集模型下三種粗糙集的決策情形。
下面通過案例對比兩種不同情況下的決策模型。

表1 病癥表現
a) 基于等價關系的概率粗糙集決策模型
(3)等價關系下的條件概率:
(4)根據以上計算所得條件概率,可做出決策如下,決策結果見表2:
表2 基于等價關系的決策情形(令= 0.4,= 0.75)
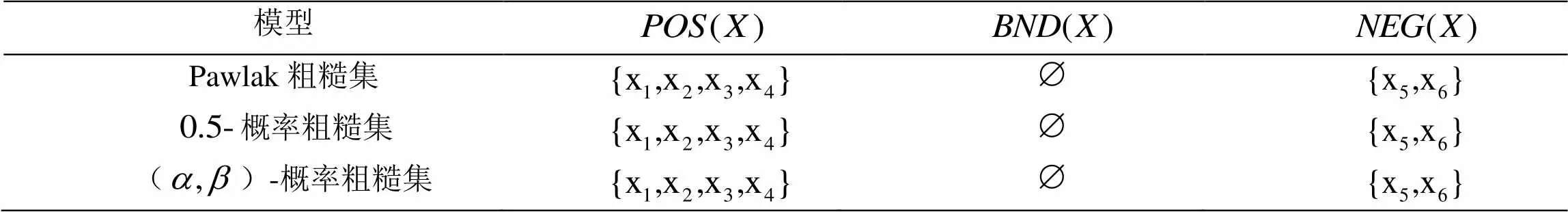
模型 Pawlak粗糙集 概率粗糙集 ()-概率粗糙集
3.2 元素最小描述并集下的概率粗糙集決策模型
(1) 對論域中的對象根據病癥分類如下:
(2) 論域U的一個覆蓋:
(3)程序運行元素最小描述結果如下:
(4)程序運行元素最小描述并集下的條件概率結果如下:
(5)根據以上計算所得條件概率,可以做出如下決策,決策結果見表3:

表 3 元素最小描述并集下的決策情形(設β= 0.4,α= 0.75)
4 結語
本文設計算法并計算了元素最小描述并集下的條件概率,分析了一般基于等價關系的概率粗糙集模型進行決策的弊端。對一般的概率粗糙集模型進行優化,給出了基于元素最小描述并集的決策粗糙集模型,并結合應用實例對兩種模型的決策結果進行了比較。
[1] Pawlak Z.Rough sets[J]. International Journal of Computer & Information Sciences, 1982, 11(5):341-356.
[2] Zakowski B W. Approximations in the space (U, Ⅱ)[J]. Demonstration Mathematical,1983,16:761-769.
[3] 薛占熬, 劉杰, 朱泰隆. 基于覆蓋的Sugeno測度粗糙集模型及其三支決策[J]. 計算機科學, 2016, 43(3): 285-290.
[4] 林姿瓊, 王敬前, 祝峰. 矩陣方法計算覆蓋粗糙集中最小、最大描述[J]. 山東大學學報(理學版),2014,49(8):97-101.
[5] 黃婧, 李進金.最小描述的多粒度覆蓋粗糙集模型[J].計算機工程與應用, 2013, 49(9): 134-149.
[6] 劉財輝,涂小強. 條件概率描述下的多粒度覆蓋粗糙集模型研究[J].計算機科學, 2015, 42(6):88-92.
[7] 張曉燕, 徐偉華, 張文修. 基于最小描述交的覆蓋廣義粗糙集[J].模糊系統與數學, 2011, 25(2):146-155.
[8] 湯建國,佘堃, 祝峰. 一種新的覆蓋粗糙模糊集模型[J].決策與支持, 2012,27(11):1653-1662.
[9] 張文修, 吳偉志, 梁吉業, 李德玉. 粗糙集理論與方法[M].北京:科學出版社, 2001.
[10] 鞏增泰, 史戰紅. 基于覆蓋的概率粗糙集模型及其Bayes決策[J]. 模糊系統與數學,2008,22(4):142-148.
[11] 鞏增泰, 柴潤麗. 基于區間值模糊概率測度的多粒度區間值決策粗糙集模型[J]. 西北師范大學學報: 自然科學版, 2015, 51(6): 21-27.
[12] 王紅, 張燕平, 錢付蘭等. EM 最優參數求解的概率粗糙集推薦算法[J]. 計算機科學與探索, 2016, 10(2): 285-292.
[13] 王輝, 黃自威, 劉淑芬. 新型加權粗糙樸素貝葉斯算法及其應用研究[J]. 計算機應用研究, 2015, 32(12):3668-3672.
[14] Yao Y Y,Wong SKM.,LingrasP. A decision-theoretic rough set model // RasZW, Methodologies for IntelligentSystems,vol.5.New York:North-Holland, 1990:17-24.
[15] 李華雄, 劉盾, 周獻中. 決策粗糙集模型研究綜述[J]. 重慶郵電大學學報(自然科學版), 2010,22(5):624-630.
[16] 趙文清, 朱永利, 高偉. 一個基于決策粗糙集理論的信息過濾模型[J].計算機工程與應用, 2007,43(7):185-187.
[17] 衷錦儀, 葉東毅. 基于模糊數風險最小化的拓展決策粗糙集模型[J]. 計算機科學, 2014,41(3):50-54.
[18] 劉盾, 李天瑞, 李華雄. 粗糙集理論: 基于三支決策視角[J].南京大學學報(自然科學版),2013,49(5):574-581.
[19] 劉盾, 李天瑞, 李華雄. 區間決策粗糙集[J]. 計算機科學,2012,39(7):178-181.
[20] 于洪, 王國胤, 姚一豫. 決策粗糙集理論研究現狀與展望[J]. 計算機學報, 2015, 38(8): 1628-1639.
[21] Zhu W,Wang F Y.Reduction and axiomization of covering generalized rough sets [J]. Information Sciences, 2003, 152:217-230.
Probabilistic Rough Set Model Based on the Union of Minimal Descriptions of Elements and Its Applications
CAI Kecan , LIU Caihui
(Department of Mathematics and Computer Science, Gannan Normal University, Ganzhou Jiangxi 341000, China)
This paper proposed a new kind of probability rough set based on the union of minimal description of elements. Some algorithms are designed for the proposed model to compute the union of minimal description of elements and corresponding probabilities. Finally, an example is employed to compare the feasibility between the existing model and the proposed model.
Rough sets; Covering; Minimal description; Probability rough sets; Decision-theoretic rough sets
1672-9129(2016)01-0048-05
TP18
A
2016-06-14;
2016-06-24。
國家自然科學基金資助項目(61305052)。
蔡克參(1992-),女,江西撫州人,碩士研究生,主要研究方向:粒計算方法在農業信息化中的應用;劉財輝(1979-),男,江西于都人,副教授,博士,主要研究方向:粗糙集、粒計算、機器學習、數據挖掘等。
(*通訊作者電子郵箱:1208008641@qq.com)

