控制增益對永磁同步電動機自抗擾控制性能的影響
左月飛 李明輝 張 捷 劉 闖 張 濤
(1.南京航空航天大學自動化學院 南京 210016 2.中國人民解放軍空軍西安航空四站裝備修理廠 西安 710077)
?
控制增益對永磁同步電動機自抗擾控制性能的影響
左月飛1李明輝2張捷1劉闖1張濤1
(1.南京航空航天大學自動化學院南京210016 2.中國人民解放軍空軍西安航空四站裝備修理廠西安710077)
在永磁同步電動機自抗擾控制系統中,當系統的實際控制增益已知時,采用實際控制增益的控制器可獲得良好的控制性能,但當系統的實際控制增益未知時,采用估計控制增益的控制器會對系統性能產生影響。將估計控制增益與實際控制增益的比值定義為增益比,分析了它對閉環系統的階躍響應、抑制噪聲性能、抗擾性能以及對連續變化輸入的跟蹤性能的影響。理論分析表明:增益比越大,則系統階躍響應的上升時間越短,抑制噪聲的效果越好,但抗擾性能越差;增益比越接近于1,系統對連續變化輸入的跟蹤性能越好。仿真和實驗驗證了理論分析的正確性。
永磁同步電動機自抗擾控制控制增益跟蹤噪聲抗擾連續變化輸入
0 引言
永磁同步電動機(Permanent Magnet Synchrounous Motor,PMSM)以其高功率/重量比、高轉矩/慣量比、高效率以及具有一定魯棒性等優點逐漸取代直流電動機和其他電勵磁的電動機,被廣泛應用于工業調速系統中。傳統的PMSM調速系統大多采用雙環線性控制結構,內環為電流環,外環為轉速環,多采用PI控制器。而PMSM是一典型的非線性、多變量耦合系統,傳統的線性PI控制難以滿足高性能的要求。
隨著永磁同步電動機非線性控制理論的發展,多種先進的復雜控制策略(如自適應控制[1,2]、模糊控制[3,4]、滑模變結構控制[5,6]等)被應用于調速系統中。盡管這些方法最終都能抑制擾動,但其依靠反饋控制,動態過程非常緩慢。一種有效提高擾動抑制效果的方法是通過擾動觀測器(Disturbance Observer,DOB)對擾動進行觀測,并前饋補償,這一思路最先由日本學者K.Ohnishi[7]提出。順著這一思路,眾多基于DOB的控制方法相繼得到應用[8-10]。與DOB具有相同功能的另一種觀測器為擴張狀態觀測器(Extended State Observer,ESO),它將內部擾動和外部擾動一起作為集總擾動,并將其擴張成一個新的狀態,因此此狀態觀測器比常規的狀態觀測器要多一個狀態。ESO可同時對狀態和擾動進行觀測。基于ESO觀測的擾動進行前饋補償的控制方法被稱為自抗擾控制(Active Disturbance Rejection Control,ADRC)[11],該方法已在工業控制領域的眾多應用場合得到了應用(如工業機器人[12]、功率變換[13]、PMSM控制等[14-16])。
在PMSM轉速一階ADRC系統中,控制增益為轉矩常數與轉動慣量的比值[17]。當系統的實際控制增益已知時,采用實際控制增益的控制器可保證系統獲得良好的控制性能。但當系統的實際控制增益未知時,如轉矩常數或轉動慣量產生變化時,采用估計控制增益的控制器將很難保證系統具有良好的控制性能[18,19]。目前,分析控制增益對系統性能影響的文獻很少。文獻[11]通過仿真說明了自抗擾控制器可使系統在實際控制增益小范圍變化時仍具有良好的控制性能。文獻[19]只定性分析了實際轉動慣量增大對系統階躍響應的影響,對于轉動慣量減小對系統的影響并未分析,也未定量分析轉動慣量對系統的影響。
本文針對PMSM轉速一階ADRC系統,將控制器中的估計控制增益與系統的實際控制增益的比值定義為增益比,分析了它對閉環系統的階躍響應、抑制噪聲性能、抗擾性能以及對連續變化輸入的跟蹤性能的影響,為控制器的參數整定提供了理論基礎。最后,通過仿真和實驗驗證了理論分析的正確性。
1 轉速環自抗擾控制器設計
1.1PMSM轉速環的數學模型
本文研究的是表貼式永磁同步電動機,則其在轉子磁場定向的同步旋轉坐標系(d-q坐標系)下的機械運動方程為
(1)
式中,J為系統的轉動慣量,kg·m2;B為系統的粘滯摩擦系數,N·m·s/rad;TL為負載轉矩,N·m;Ω為機械角速度,rad/s;Kt為轉矩常數,N·m/A_peak;iq為交軸電流,A_peak。
采用直軸電流為零,即id*=0的矢量控制方式。
由式(1)可得機械角速度狀態方程為
(2)
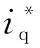
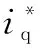
(3)
1.2反饋控制律設計
如果系統實際控制增益的大小未知,可將其假設為best,即假設系統的狀態方程為
(4)
定義角速度跟蹤誤差es=Ω*-x1,則跟蹤誤差狀態方程為
(5)
采用線性比例反饋控制律,即
(6)
式中,kps為控制器的比例系數。
結合式(5)和式(6)可得系統控制量為
(7)
式(7)中的實際狀態x1和x2未知,可通過傳感器測量或用觀測器對其進行觀測。
1.3二階線性ESO的設計
對式(3)構建二階線性ESO為
(8)
式中,z1、z2分別為x1(角速度)、x2(擾動項)的觀測值;e1為ESO對x1的觀測誤差;β1和β2為觀測器系數。
將式(8)與式(3)相減可得
(9)
式中,ESO的特征多項式為λ(s)=s2+β1s+β2,令其為理想的特征多項式(s+p)2,則β1=2p、β2=p2,-p為ESO的閉環極點,p也可稱為觀測器帶寬。
由式(8)、式(9)可得狀態x1、x2的估計量為
(10)
從式(10)可看出,z1近似為x1濾波后的值,通常可認為z1≈x1,對于測量噪聲較大的系統,用z1代替x1作為反饋可顯著減小系統的噪聲;z2是x2經二階低通濾波后的信號,通常可認為z2≈x2。
將式(7)中的x1、x2分別用z1、z2代替,可得控制量為
(11)
限幅后的實際控制量為
(12)
綜上可得轉速環一階自抗擾控制器的結構框圖如圖1所示。
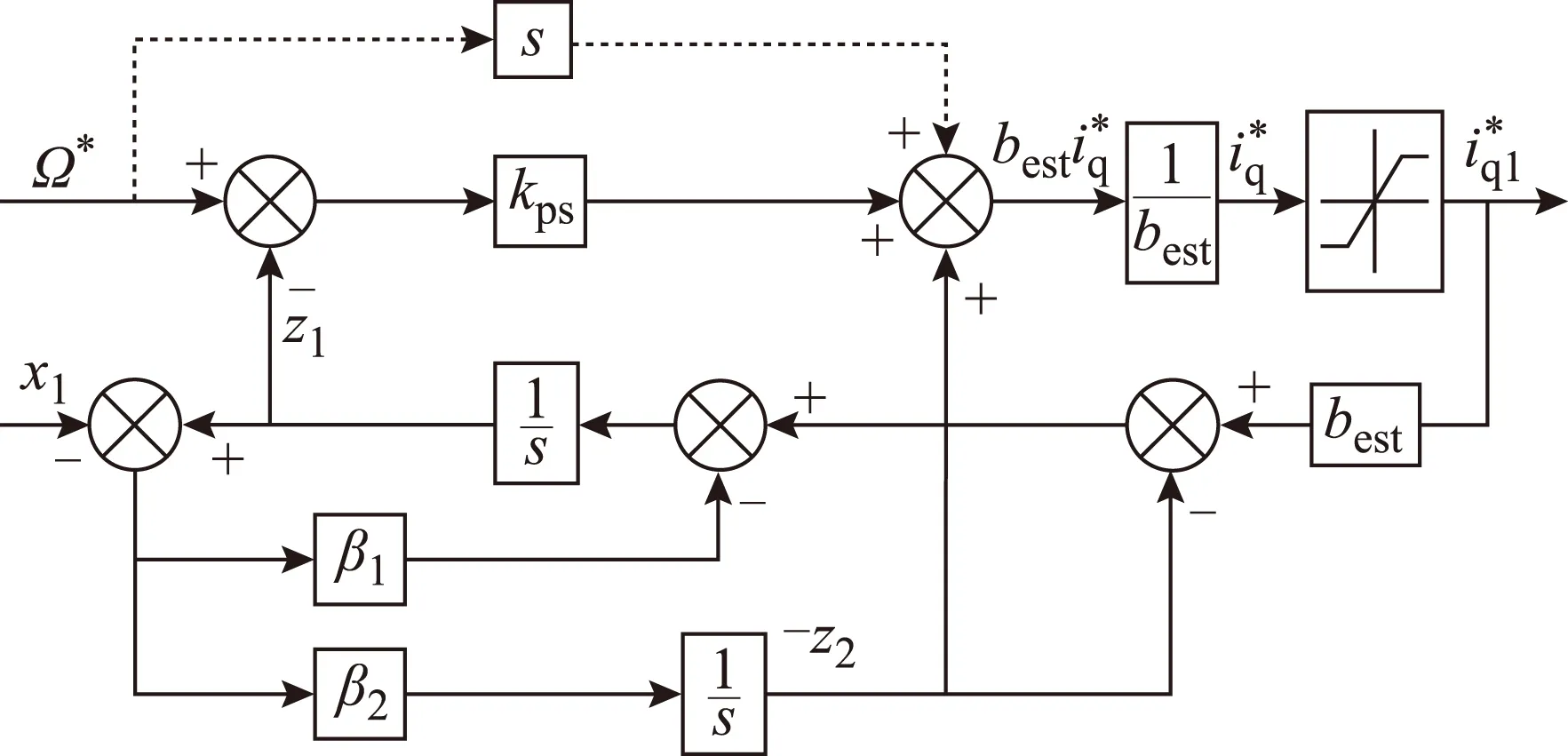
圖1 轉速環一階自抗擾控制器Fig.1 First-order ADRC controller of speedloop
1.4系統響應
為分析方便,以下分析過程中忽略電流跟蹤誤差和電流限幅的影響。
由式(10)、式(11)可得
(13)
(14)
定義增益比c=best/b,由式(3)、式(13)得系統在給定Ω*(s)和擾動x2(s)作用下的傳遞函數分別為
(15)
式中,Γ為閉環系統的特征多項式,Γ=cs3+c(β1+kps)s2+(β2+β1kps)s+β2kps。
2 增益比c對系統性能的影響
2.1增益比c對階躍響應的影響
當系統輸入為階躍信號時,輸入的微分為脈沖信號,輸入微分前饋幾乎不起作用,因此系數在給定Ω*(s)作用下的閉環傳遞函數可近似為
(16)
由式(16)可看出,系統的閉環零點與ESO的閉環極點相同,通常離虛軸較遠,閉環系統的極點為特征方程Γ=0的根。將閉環系統特征方程改寫為
(17)
取p=500、kps=36,則式(17)代表的以c為參數的根軌跡如圖2所示。
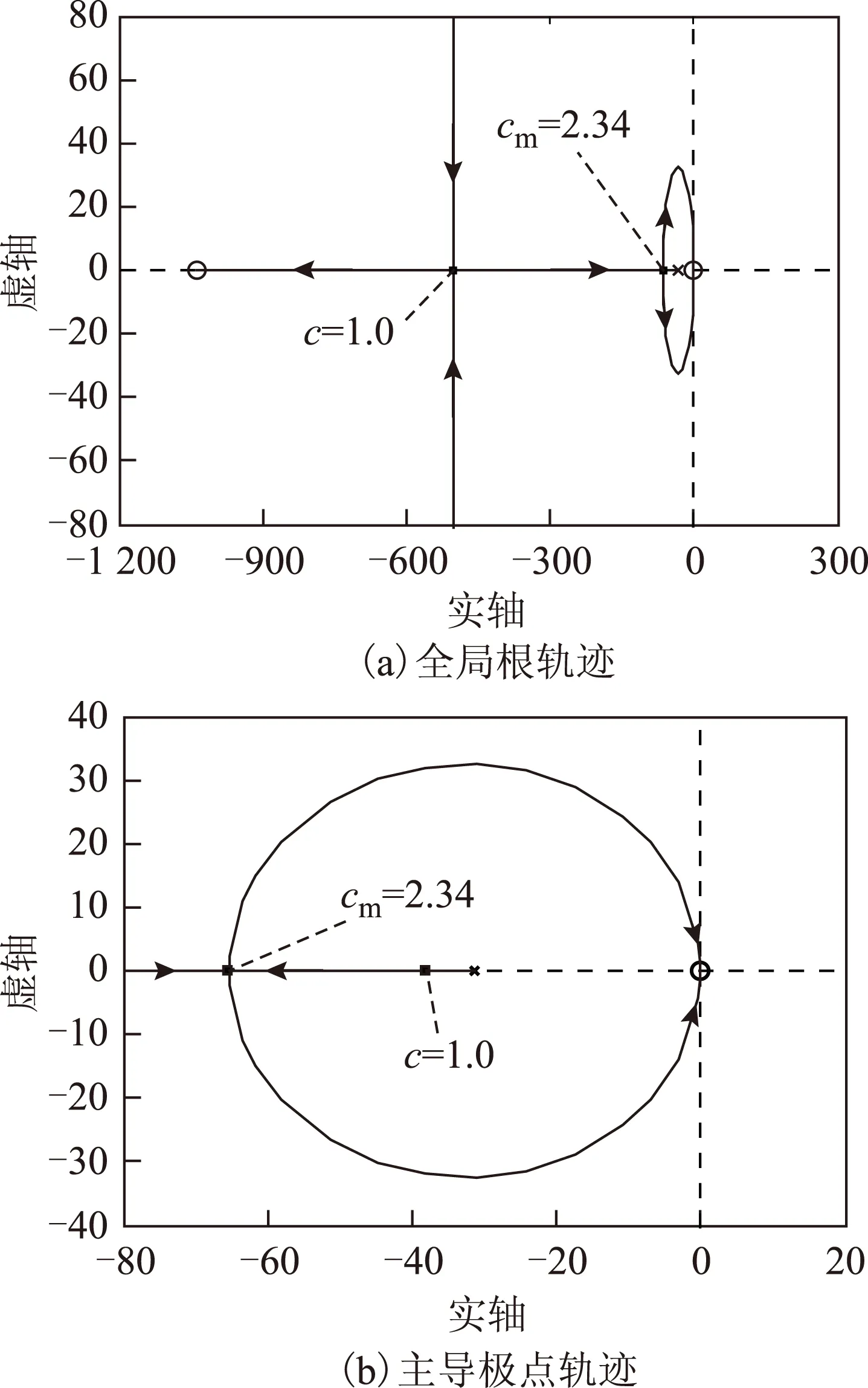
圖2 系統在c變化時的根軌跡Fig.2 Root locus of the system when c varying
容易證明,閉環系統特征方程Γ=0不存在共軛復根的條件是1≤c≤cm。其中,cm的計算公式為
(18)
當p=500、kps=36時,cm=2.34。
由圖2可得出以下結論:
1)當c>cm時,閉環系統的特性方程有一對離虛軸較近的共軛復根,還有一個離虛軸較遠的實根,階躍響應存在超調,且超調量隨c的增大而增大。
2)當1≤c≤cm時,閉環系統的特征方程具有3個實根,階躍響應不存在超調,c越大,則閉環系統的主導極點離虛軸越遠,系統響應速度越快。
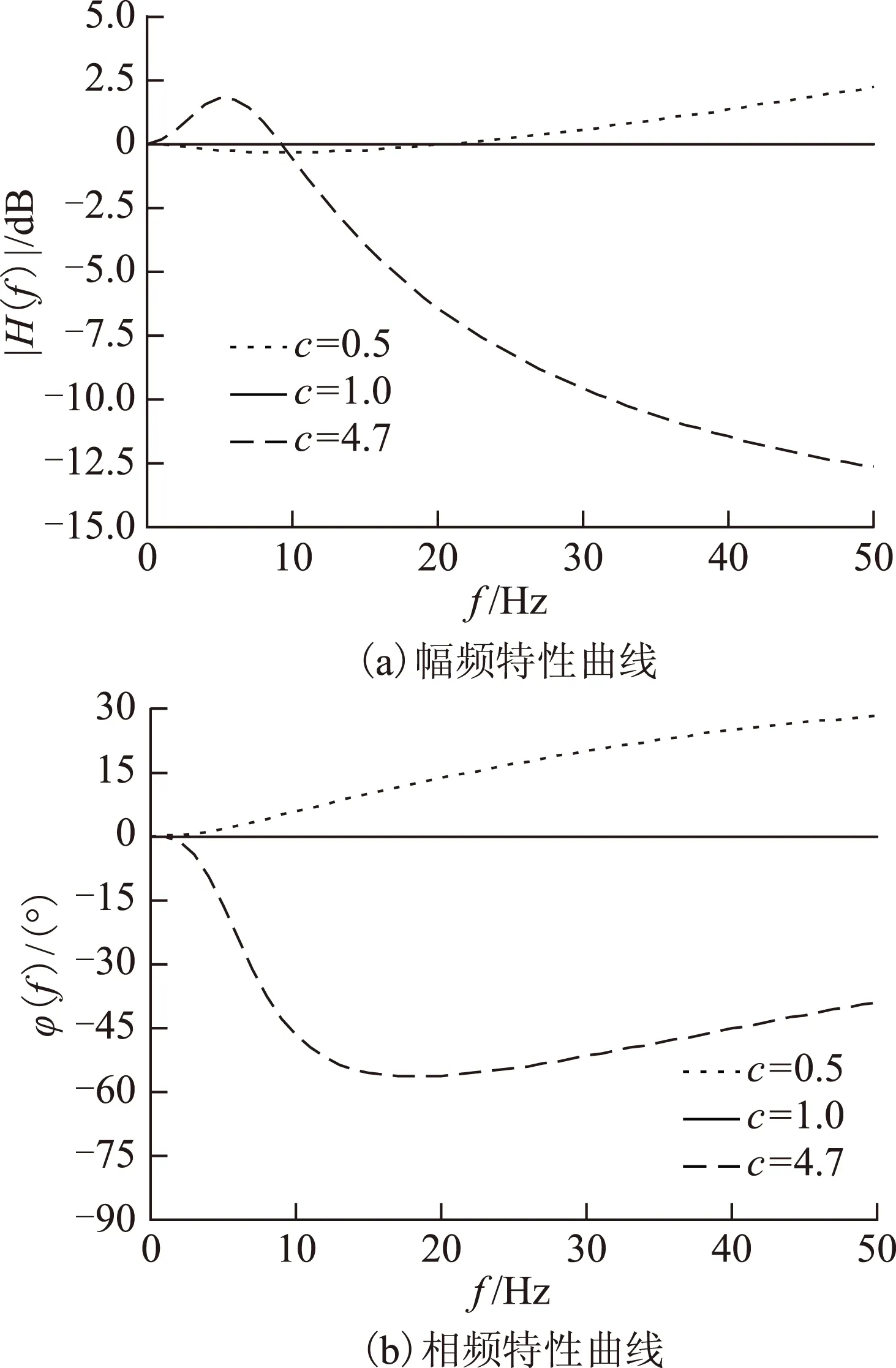
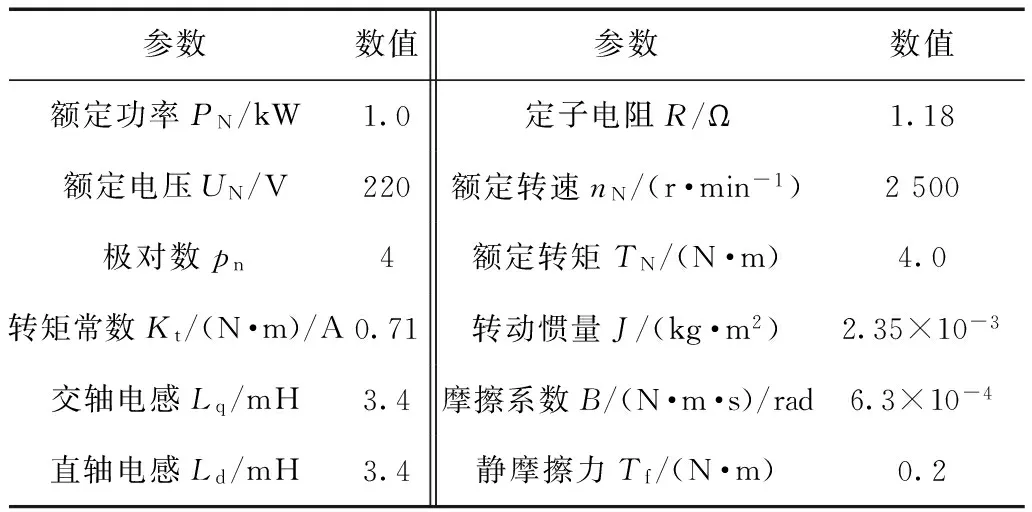
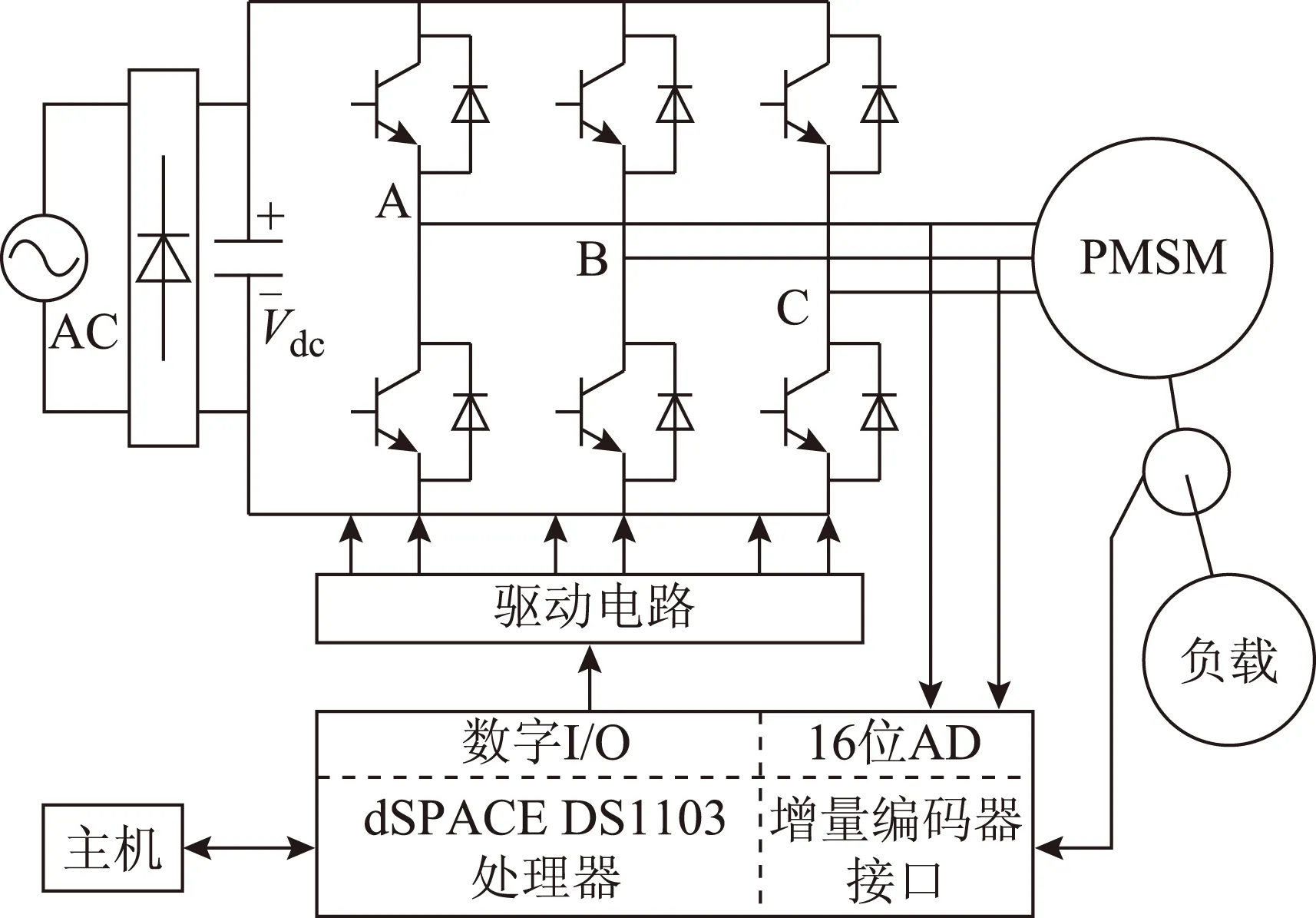
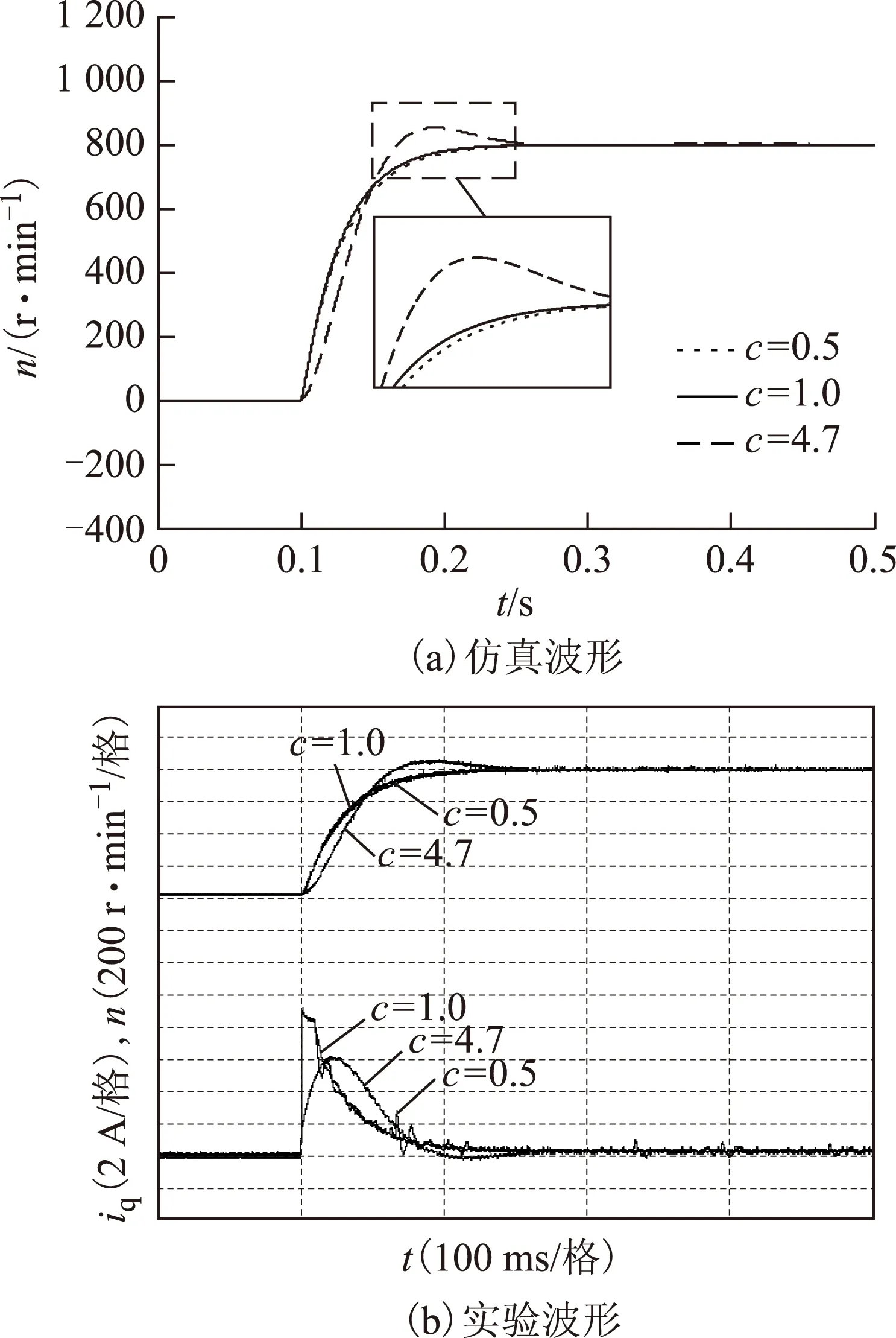
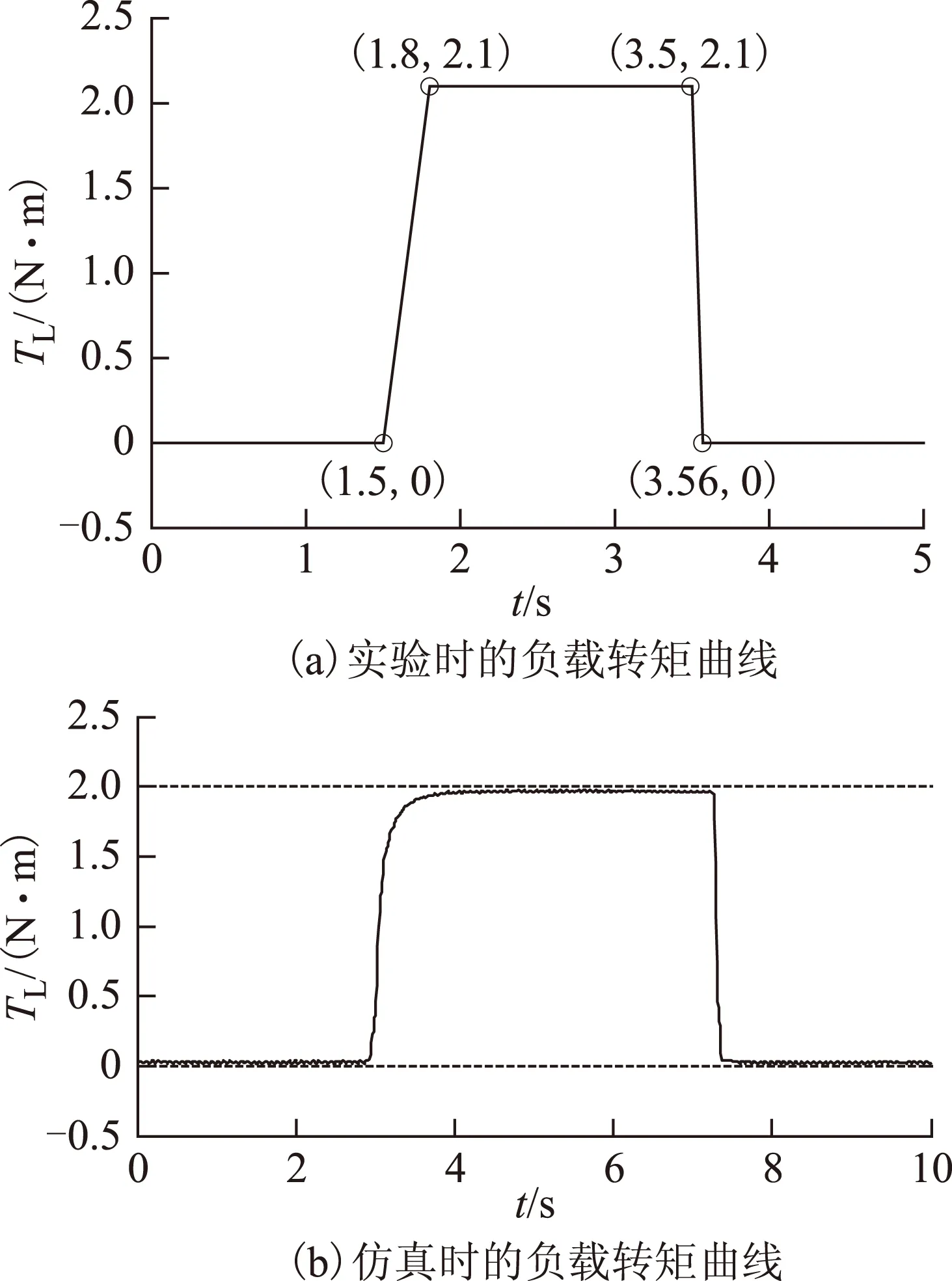
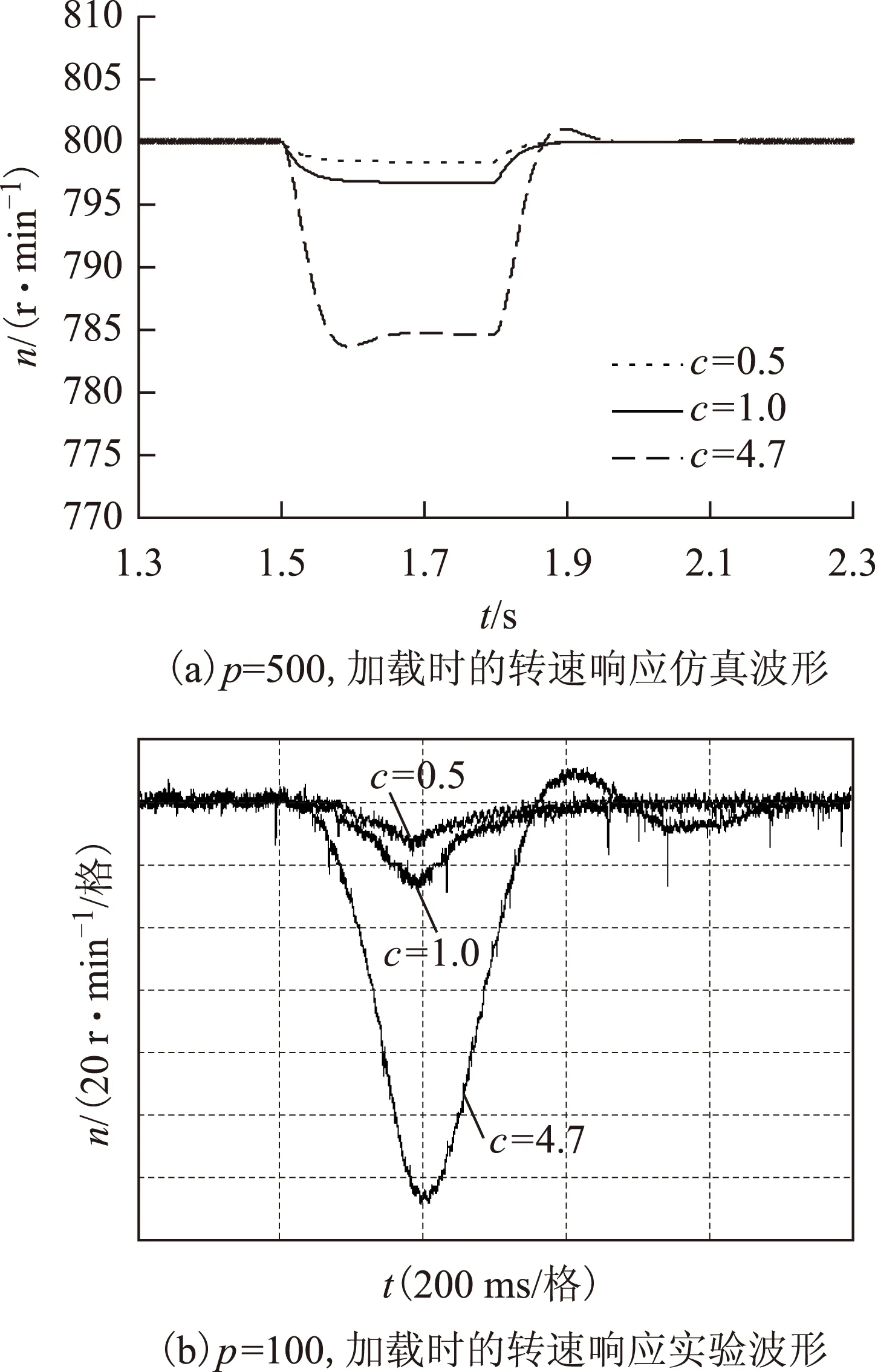
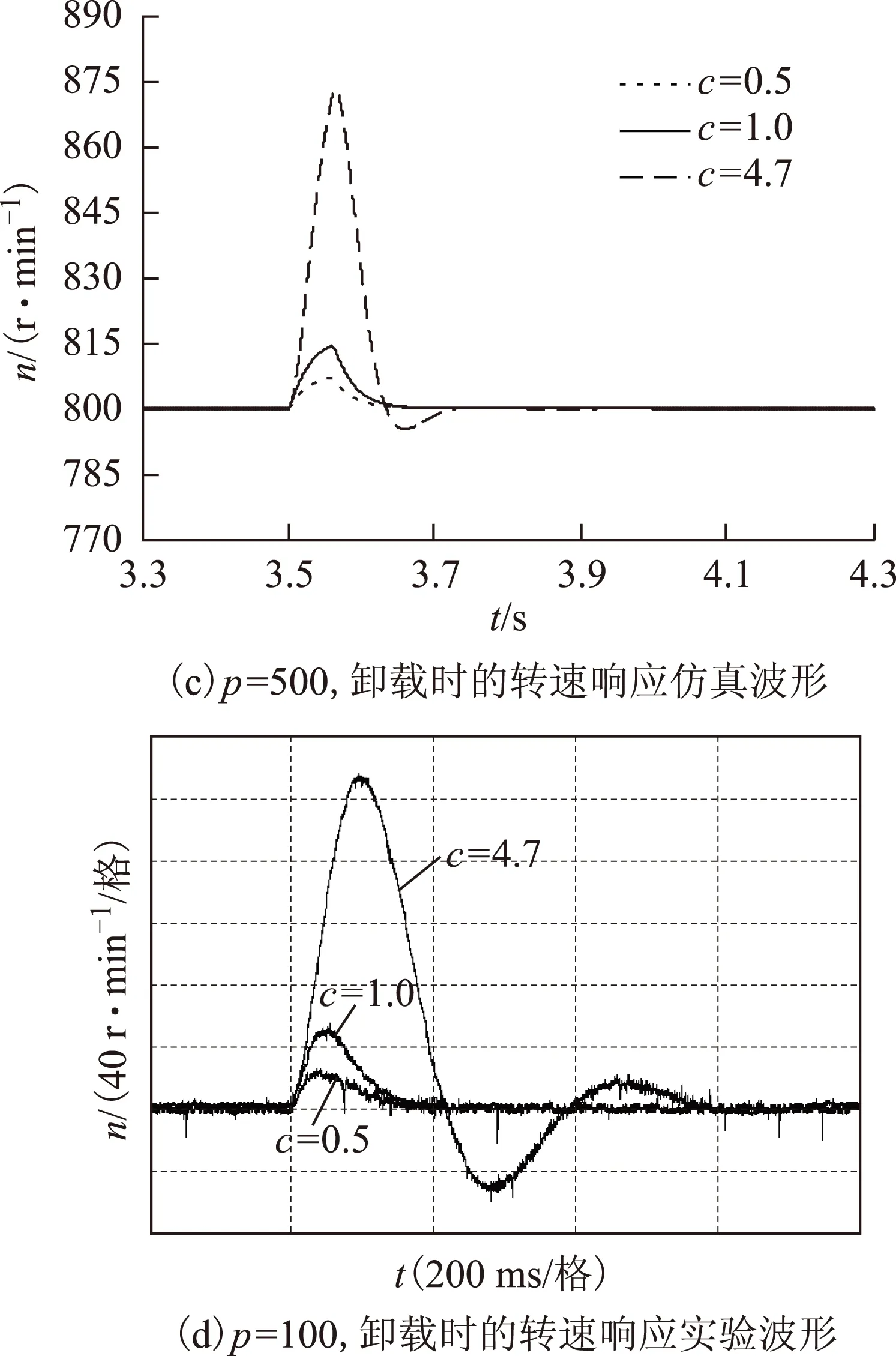
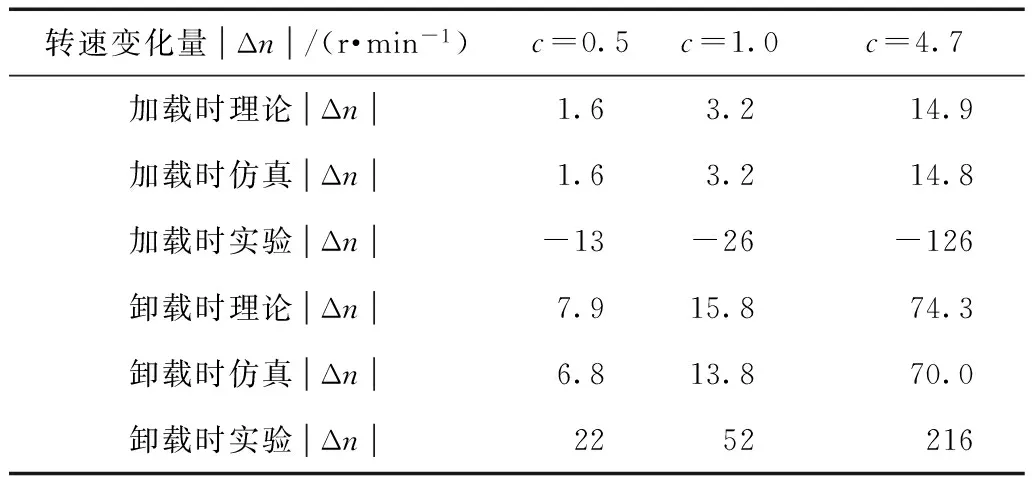
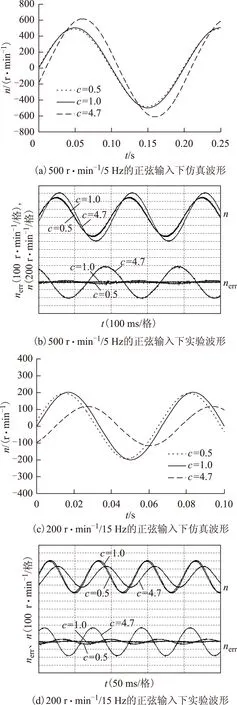
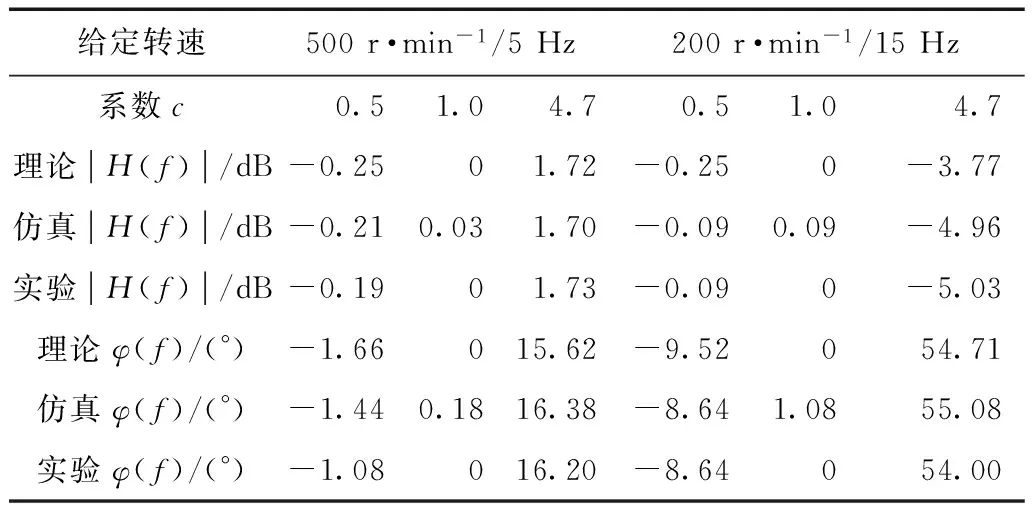
3)當0 2.2增益比c對抗擾性能的影響 由式(15)可得系統在擾動x2(s)作用下的傳遞函數為 (19) 當p=500、kps=36時,式(19)表示的閉環傳遞函數的幅頻特性曲線和相頻特性曲線如圖3所示。 圖3 抗擾傳遞函數的波特圖Fig.3 Bode diagram of disturbance rejecting transfer function 由式(19)可看出,擾動作用下的轉速變化量與擾動變化率及c呈正比。由圖3可看出,增益比c越小,則抗擾系統的低頻增益越小,但中頻增益有所增大。即c越小,系統的抗低頻擾動性能越好,但有可能導致系統產生共振(共振頻率為中高頻)。 2.3增益比c對跟蹤連續變化輸入性能的影響 以正弦給定為例,輸入的微分為余弦,此時輸入微分前饋能夠起作用,因此系統在給定Ω*(s)作用下的閉環傳遞函數為 (20) 當p=500、kps=36時,式(20)表示的閉環傳遞函數的幅頻特性曲線和相頻特性曲線如圖4所示。由圖4可看出: 1)當c<1時,系統輸出的相位超前于輸入,低頻下的系統輸出幅值小于輸入,而中高頻下的系統輸出幅值大于輸入。 2)當c=1時,系統輸出能夠完全跟蹤輸入。 3)當c>1時,系統輸出的相位滯后于輸入,低頻下的系統輸出幅值大于輸入,而中高頻下的系統輸出幅值則小于輸入。 圖4 跟蹤傳遞函數的波特圖Fig.4 Bode diagram of the tracking transfer function 由以上分析結果可知,c減小會導致系統的高頻成分增加,與通過根軌跡分析系統階躍響應所得到的結果一致。另外,當c未知時,可利用c=1時的系統對連續變化輸入跟蹤較好這一特性,通過實驗得到近似的系統實際控制增益。 綜上,從系統的階躍響應考慮,則希望c在滿足c≤c1的條件下盡量大;從抗擾性能考慮,則希望c盡量小;從對連續變化輸入的跟蹤性能考慮,則希望c=1,即希望估計的控制增益等于實際控制增益。 為進一步驗證理論分析的正確性,本文對永磁同步電動機調速系統進行了仿真和實驗,仿真和實驗中所用的PMSM參數如表1所示。 表1 電動機參數Tab.1 Motor parameters 永磁同步電動機調速系統的實驗平臺采用基于dSPACE實時仿真系統DS1103,利用快速原型法通過Simulink自動完成代碼的生成與下載。實驗中的逆變器開關頻率為10 kHz,通過PWM中斷觸發電流采樣和占空比的更新。系統的硬件結構框圖和實驗平臺分別如圖5和圖6所示。 圖5 系統硬件結構框圖Fig.5 System hardware block diagram 圖6 實驗平臺Fig.6 Experiment platform 轉速環和電流環采樣周期以及系統的計算步長均為0.1 ms。為便于分析,對系統參數進行了標幺化,選取轉速基值nbase=3 000 r·min-1。控制器參數設置為:kps=36、p=500,設置c分別為0.5、1.0和4.7。兩個電流環中的PI控制器參數設置為kpi=0.1,kii=500。如無特別說明,實驗中其余參數均與仿真中的相同。 3.1驗證增益比c對階躍響應的影響 在t=0.1 s時,轉速給定由0 r·min-1階躍變化至800 r·min-1,仿真波形和實驗波形分別如圖7所示。由實驗波形可看出,c越大,系統階躍響應的上升時間越短,系統高頻噪聲越小,其中的電流噪聲是由轉速計算存在噪聲導致的。當c=4.7(大于2.34)時,階躍響應存在超調;當c=1.0時,階躍響應的超調消失;當c=0.5時,階躍響應同樣不存在超調,但iq中的噪聲較大。以上仿真和實驗結果均與理論分析結果一致,驗證了理論分析的正確性。 圖7 空載起動時的動態響應Fig.7 Dynamic response when start without load 3.2驗證增益比c對抗擾性能的影響 圖8 仿真和實驗所用的負載曲線Fig.8 Load curve used in simulation and experiment 圖9 不同c下負載擾動時的動態響應Fig.9 Dynamic response under the effect of load disturbance表2 負載擾動作用下的轉速變化量Tab.2 Speed variation under the effect of load disturbance 轉速變化量Δn/(r·min-1)c=0.5c=1.0c=4.7加載時理論Δn1.63.214.9加載時仿真Δn1.63.214.8加載時實驗Δn-13-26-126卸載時理論Δn7.915.874.3卸載時仿真Δn6.813.870.0卸載時實驗Δn2252216 由表2可看出,加載時的轉速變化量與理論計算值一致,與c呈正比。在未考慮電流跟蹤誤差的影響時,轉速變化量理論上與擾動變化率呈正比,即卸載時的轉速變化量應是加載時的-5倍。由于卸載時負載變化較快,負載變化率為一窄脈沖,轉速響應并未達到穩態,因此轉速變化量比理論值小。由于實驗中ESO的帶寬p比仿真中的值小,ESO對擾動的觀測速度變慢,轉速變化量比仿真結果大,但c越小時系統抗擾性能越強的結論仍然正確,驗證了理論分析的正確性。 3.3驗證增益比c對跟蹤時變輸入性能的影響 分別給定500 r·min-1/5 Hz和200 r·min-1/15 Hz的正弦型轉速,仿真波形和實驗波形分別如圖10所示,仿真與實驗數據如表3所示。 圖10 跟蹤正弦給定時的動態響應Fig.10 Dynamic response of tracking sine reference 由圖10可看出,在500 r·min-1/5 Hz的正弦輸入下,當c=0.5時,系統輸出的幅值小于給定,且相位超前于給定;當c=4.7時,系統輸出的幅值大于給定,且相位滯后于給定;c=1.0時的系統跟蹤效果最好。在200 r·min-1/15 Hz的正弦輸入下,當c=0.5時,系統輸出的幅值大于給定,且相位超前于給定;當c=4.7時,系統輸出的幅值小于給定,且相位滯后于給定;c=1.0時的系統跟蹤效果最好。由圖10和表3可看出,仿真結果和實驗結果均與理論分析結果一致,證明了理論分析的正確性。 表3 不同c時跟蹤正弦輸入下的動態響應Tab.3 Dynamic response of tracking sine reference with different parameter c 本文將自抗擾控制器的估計控制增益與系統的實際控制增益的比值定義為增益比c,通過傳遞函數分析了它對系統的階躍響應、抗擾性能以及跟蹤時變輸入性能的影響。分析結果表明,從系統的階躍響應考慮,則希望c在滿足c≤cm的條件下盡量大;從抗擾性能考慮,則希望c盡量小;從對連續變化輸入的跟蹤性能考慮,則希望c=1。在實際系統中,可根據具體的性能要求適當調節c。當c未知時,可利用c=1時的系統對時變輸入跟蹤較好這一特性,通過實驗得到系統的近似控制增益。通過仿真和實驗驗證了理論分析的正確性。 [1]魯文其,胡育文,梁驕雁,等.永磁同步電機伺服系統抗擾動自適應控制[J].中國電機工程學報,2011,31(3):75-81. Lu Wenqi,Hu Yuwen,Liang Jiaoyan,et al.Anti-disturbance adaptive control for permanent magnet synchronous motor servo system[J].Proceedings of the CSEE,2011,31(3):75-81. [2]梁驕雁,胡育文,魯文其.永磁交流伺服系統的抗擾動自適應控制[J].電工技術學報,2011,26(10):174-180.Liang Jiaoyan,Hu Yuwen,Lu Wenqi.Anti-disturbance adaptive control of permanent magnet AC servo system[J].Transactions of China Electrotechnical Society,2011,26(10):174-180. [3]崔家瑞,李擎,張波,等.永磁同步電機變論域自適應模糊PID控制[J].中國電機工程學報,2013,33(S1):190-194. Cui Jiarui,Li Qing,Zhang Bo,et al.Permanent magnet synchronous motor of variable universe adaptive fuzzy PID Control[J].Proceedings of the CSEE,2013,33(S1):190-194. [4]張洪帥,王平,韓邦成.基于模糊PI模型參考自適應的高速永磁同步電機轉子位置檢測[J].中國電機工程學報,2014,34(12):1889-1896. Zhang Hongshuai,Wang Ping,Han Bangcheng.Rotor position measurement for high-speed permanent magnet synchronous motors based on fuzzy PI MRAS[J].Proceedings of the CSEE,2014,34(12):1889-1896. [5]汪海波,周波,方斯琛.永磁同步電機調速系統的滑模控制[J].電工技術學報,2009,24(9):71-77. Wang Haibo,Zhou Bo,Fang Sichen.A PMSM sliding mode control system based on exponential reaching law[J].Transactions of China Electrotechnical Society,2009,24(9):71-77. [6]張曉光,趙克,孫力,等.永磁同步電機滑模變結構調速系統動態品質控制[J].中國電機工程學報,2011,31(15):47-52. Zhang Xiaoguang,Zhao Ke,Sun Li,et al.Sliding mode control of permanent magnet synchronous motor based on a novel exponential reaching law[J].Proceedings of the CSEE,2011,31(15):47-52. [7]Ohnishi K.A new servo method in mechatronics[J].Transoctions of Japanese Society of Electrical Engineering,1987,107:83-86. [8]Komada S,Ishida M,Ohnishi K,et al.Disturbance observer-based motion control of direct drive motors[J].IEEE Transactions on Energy Conversion,1991,6(3):553-559. [9]劉穎,周波,方斯琛.基于新型擾動觀測器的永磁同步電機滑模控制[J].中國電機工程學報,2010,30(9):80-85. Liu Ying,Zhou Bo,Fang Sichen.Sliding mode control of PMSM based on a novel disturbance observer[J].Proceedings of the CSEE,2010,30(9):80-85. [10]張曉光,孫力,趙克.基于負載轉矩滑模觀測的永磁同步電機滑模控制[J].中國電機工程學報,2012,31(3):111-116. Zhang Xiaoguang,Sun Li,Zhao Ke.Sliding mode control of PMSM based on a novel load torque sliding mode observer[J].Proceedings of the CSEE,2012,31(3):111-116. [11]韓京清.自抗擾控制技術——估計補償不確定因素的控制技術[M].北京:國防工業出版社,2008. [12]劉昊,王濤,范偉,等.氣動人工肌肉關節的自抗擾控制[J].機器人,2011,33(4):461-466,508.Liu Hao,Wang Tao,Fan Wei,et al.Active disturbance rejection control for the joint by PMAs[J].Robot,2011,33(4):461-466,508. [13]鄧文浪,令弧文娟,朱建林.應用自抗擾控制器的雙級矩陣變換器閉環控制[J].中國電機工程學報,2008,28(12):13-19. Deng Wenlang,Linghu Wenjuan,Zhu Jianlin.Closed-control for two-stage converter based on auto-disturbance rejection controller[J].Proceedings of the CSEE,2008,28(12):13-19. [14]閆光亞,艾武,陳冰,等.永磁直線同步電機ADRC控制系統[J].電工技術學報,2011,26(9):60-66. Yan Guangya,Ai Wu,Chen Bing,et al.PMLSM active disturbance rejection control[J].Transactions of China Electrotechnical Society,2011,26(9):60-66. [15]Li Shihua,Xia Cunjian,Zhou Xuan.Disturbance rejection control method for permanent magnet synchronous motor speed-regulation system[J].Mechatronics,2012,22(6):706-14. [16]盧達,趙光宙,曲軼龍,等.永磁同步電機無參數整定自抗擾控制器[J].電工技術學報,2013,28(3):27-34. Lu Da,Zhao Guangzhou,Qu Yilong,et al.Permanent magnetic synchronous motor control system based on no manual tuned active disturbance rejection control[J].Transactions of China Electrotechnical Society,2013,28(3):27-34. [17]李世華,丁世宏,都海波,等.非光滑控制理論與應用[M].北京:科學出版社,2013. [18]劉志剛,李世華.基于永磁同步電機模型辨識與補償的自抗擾控制器[J].中國電機工程學報,2008,28(24):118-123. Liu Zhigang,Li Shihua.Active disturbance rejection controller based on permanent magnetic synchronous motor model identification and compensation[J].Proceedings of the CSEE,2008,28(24):118-223. [19]Li Shihua,Liu Zhigang.Adaptive speed control for permanent-magnet synchronous motor system with variations of load inertia[J].IEEE Transactions on Industrial Electronics,2009,56(8):3050-3059. Influence of Control Gain on Active Disturbance Rejection Controller for PMSM Zuo Yuefei1Li Minghui2Zhang Jie1Liu Chuang1Zhang Tao1 (1.College of AutomationNanjing University of Aeronautics and AstronauticsNanjing210016China 2.The Fourth Aerospace Station of the Chinese People’s Liberation Army Air ForceXi’an710077China) In the active disturbance rejection control (ADRC) system for the permanent magnet synchronous motor (PMSM),a good control performance can be gotten when the control gain is known.An estimated control gain,used in the ADRC controller when the control gain of the system is unknown,will affect the control performance.In this paper,the ratio between the estimated control gain and the real control gain is defined as the control gain ratio,whose effects on the step response,the noise immunity,the ability of rejecting disturbance,and the performance of continuously tracking the varying input is also analyzed.Theoretically analysis indicates that the shorter rising time of the step response and the better noise immunity while the worse disturbance rejection ability will be acquired with higher control gain ratio.Meanwhile,the advanced tracking performance will be achieved when the ratio approaches one.The Extensive simulation and experiment tests are performed to verify these conclusions. Permanent magnet synchronous motor (PMSM),active disturbance rejection control (ADRC),control gain,tracking,noise,disturbance rejection,continuously varying input 2015-01-16改稿日期2015-11-25 TM351 左月飛男,1989年生,博士研究生,研究方向為永磁電機控制。 E-mail:zuo@nuaa.edu.cn(通信作者) 李明輝男,1975年生,中級工程師,研究方向為機電系統控制。 E-mail:13310988686@189.cn 國家自然科學基金(51377076)、江蘇省“六大人才高峰”項目(YPC13013)和江蘇省產學研資金(BY2014003-09)資助。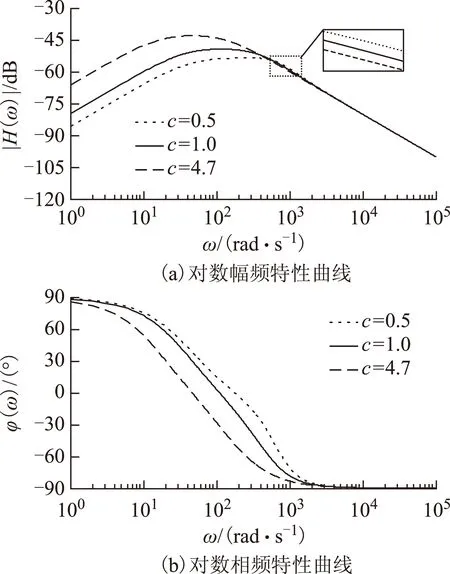
3 仿真分析與實驗驗證

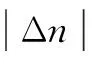
4 結論

