大壩沉降監測的時間序列與預報
□裴 锫(山西水利水電勘測設計研究院)
大壩沉降監測的時間序列與預報
□裴锫(山西水利水電勘測設計研究院)
基于平穩性時間序列分析理論,對大壩沉降監測數據時間序列進行模式識別、參數估計,建立變形監測分析與預報的A RM A模型。結合實例,運用該模型對變形監測數據進行動態分析和預報,將擬合和預報數據同原始數據進行比較分析,結果表明A RM A模型處理動態監測數據是十分可行和有效的,具有重要的應用價值。
平穩序列;時間序列;變形監測;分析和預報
0 引言
大壩的建設是利國利民的重大舉措,其安全性顯得尤為重要。隨著時間的推移,由于某些因素的影響大壩有可能發生沉降、傾斜等變形,而這種變形如果超過合理的限度,將會影響到它的正常使用,甚至對其安全造成威脅。為了避免這種變形可能造成的潛在威脅,需要對它們進行定期監測,分析其變形規律并作出相應的預報。目前,對變形監測數據處理的方法很多,有回歸分析、時間序列分析法、灰色系統理論、神經網絡法等。時間序列法是一種動態數據處理方法,利用觀測數據之間的自相關性建立相應的數學模型來描述監測對象的變化規律與特征,并預測其未來的變化。文章采用時間序列方法對某大壩監測數據進行處理,取得了較好的擬合效果和較高的預測精度。
1 平穩時間序列的模型建立與預報
1.1監測數據的平穩化處理
大量地表監測數據特征表明,沉降量序列是由沉降量趨勢項和沉降量平穩序列兩部分組成。沉降量序列可表示為:

式中,{St}表示沉降量序列,{Ht}表示沉降量趨勢項,{Xt}表示沉降量平穩序列。
現對監測數據進行平穩化處理,運用差分方法消除趨勢項。若設Ht=at+b,采用一階差分▽St=St-St-1=a+Xt-Xt-1=a+▽Xt,a為常數,將▽稱為差分算子。當趨勢項是時間t的一次函數時,通過一階差分建立起平穩時間序列{▽St}。同樣地,如果趨勢項Ht是時間t的二次函數時,設Ht=at2+bt+c,▽2St=▽St-▽St-1=▽2Xt,通過二階差分,就可建立起平穩性時間序列{▽2St}。
1.2時間序列原理及模型
對于平穩、正態、零均值的時間序列{Xt},其取值不僅與前p個,取值Xt-1,Xt-2,L,Xt-p有關,而且還與前q步的各個干擾at-1,at-2,…,at-p有關,得到一般的ARMA模型:

式中,(i=1,2,L,p)稱為自回歸參數φi,(i=1,2,,q)稱為滑動平均參數,ai(i=t-q,,t-2,t-1,t)為白噪聲序列,同時a~N(0,б2)。式(2)稱為自回歸滑動平均模型,記為ARMA(p,q)。當=0時,式(2)變成

式(3)稱為p階自回歸模型,記為AR(p)。當φi=0時,式(2)變成

式(4)稱為q階滑動平均模型,記為MA(q)。
1.3模型類型與階數的確定
由于沉降量序列在消除了趨勢項后,就由非平穩序列轉化為平穩序列,因而可選用自回歸AR(p)模型。設X1,X1,L,XN為零均值的時間序列{Xt}的其中一組樣本觀測值,下面以此樣本觀測值為例介紹AR(p)模型一般建模步驟。
樣本自協方差函數為:
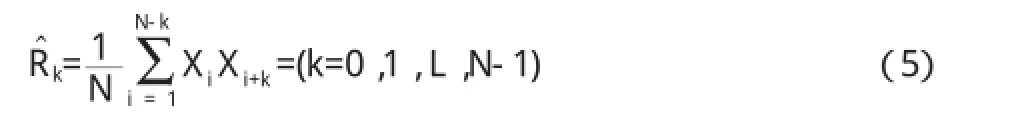

1.3.3模型參數的估計
平穩時間序列{Xt}可用AR模型表示為:

式中YN=(Xp+1,Xp+2,L,XN)T,ФN=(φ1,φ2,L,φp)T,AN=(zp+1,zp+2, L,zn1)T

根據最小二乘理論,參數最小二乘估計為

求得參數φ1,φ1,L,φp后,就可以根據(3)式對樣本監測數據進行預報。
2 實例計算與分析
以福建省某大壩部分監測點的沉降監測數據為例,采用時間序列方法對其中ⅡR1-1、ⅡR1-3兩個點的沉降量進行變形分析與預測。提取監測點的34期數據,用前29期數據建立時間序列模型,并對后5期進行沉降預測,同時與原始沉降量進行比較驗證。提取ⅡR1-1點的數據進行分析計算。
首先對監測數據進行平穩性檢驗,發現ⅡR1-1點呈明顯的下降趨勢,為不平穩序列,因此需要進行平穩化處理。采用二次差分的方式,得到的數據序列消除了逐漸下降的趨勢,可視為寬平穩性時間序列,記為{Xt},該序列滿足平穩、零均值的條件。分別計算{Xt}的自相關函數和偏相關函數,見表1。
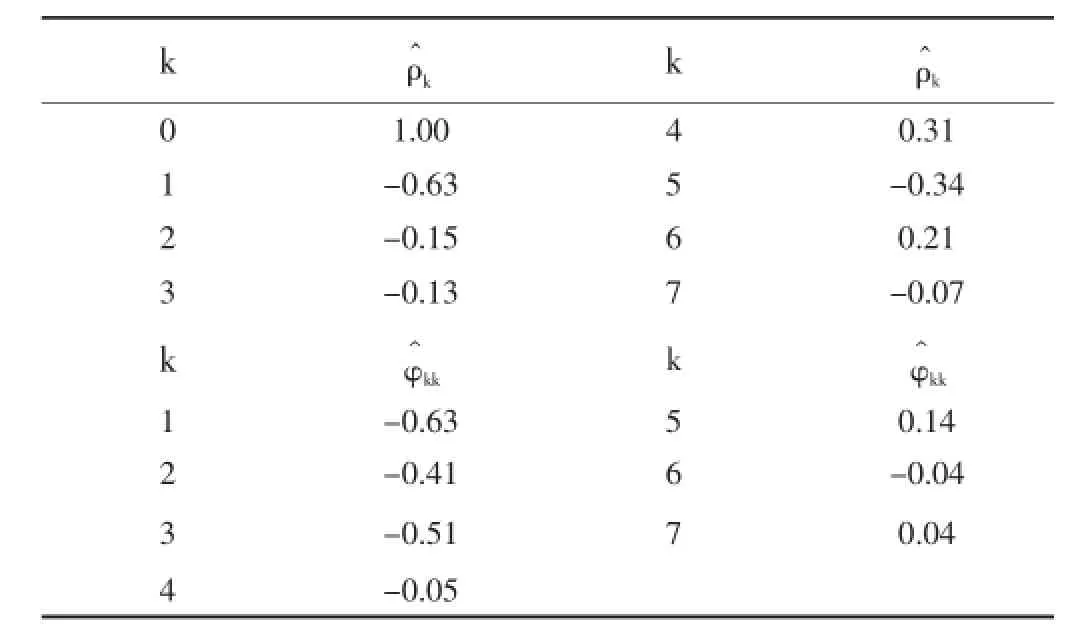
表1 自相關函數值和偏相關函數值表
利用平穩序列{Xt}建立自回歸AR(p)模型,根據偏相關函數的截尾特性,確定階數為3σ。同原理,當k>p時逐漸服從正態分布N(0,1/N),對每個p>0分別計算+M,p+M,以此確定自回歸模型的階數為3。根據式(6),運用最小二乘方法進行參數估計,求得φ1=-1.16,φ2=-0.93,φ3=-0.55。得到序列{Xt}的AR(3)模型:

由于序列{Xt}由{St}二次差分得到,由此得到

利用該模型求監測點ⅡR1-1的前29期模型擬合值并與實測值進行比較。結果發現絕大多數都比較吻合,相差都在1mm以內,擬合精度較高。采用此AR(3)模型對該點后5期(30~34期)進行預報,預報殘差結果見表2。

表2 ⅡR1-1點預測結果比較表(單位:mm)
從表2可以看出,ⅡR1-1點的后5期預報效果比較滿意,精度較高,相差都在0.50mm以內,可以比較準確地反映出監測點的沉降變化規律。為了更客觀地驗證該模型的準確性,同時對ⅡR1-3點后5期沉降量進行預測,見表3。
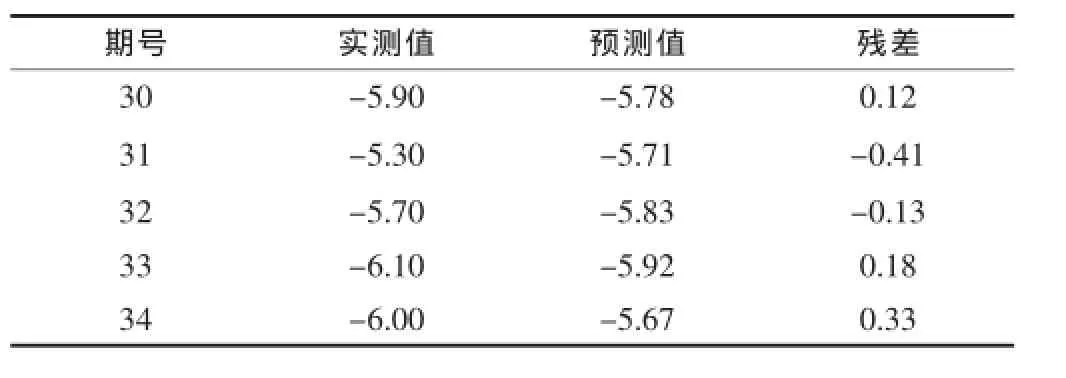
表3 ⅡR1-3點預測結果比較表(單位:mm)
從表3看出,此模型對ⅡR1-3點的預報精度也比較高。因此可以看出,采用AR(3)模型對ⅡR1-1和ⅡR1-3監測點進行擬合分析和短期預報都取得了比較理想的效果。
3 結論
對于平穩性動態監測數據,采用時間序列方法對其進行分析與預報是可行而且有效的,并且通過動態監測數據建立的時間序列模型能夠準確地反映動態數據之間的內在關系及監測點的變化特征與規律。將時間序列方法應用于大壩沉降監測數據序列,具有建模容易、計算方便簡單和預報快速、準確的特點,同時采用時間序列模型對監測點進行短期預報效果較好,隨著預測的步長增加,預測精度有所降低,因此應盡量用時間序列進行短期預報。
(責任編輯:左英勇)
P2-0
B
1673-8853(2016)08-0092-02
2016-03-23

