葉素動量理論（BEM）實現方法討論

葉素動量理論（BEM）實現方法討論

葉素動量理論（BEM）是翼式流體機械葉片設計中廣泛采用的方法，它通過求解一組代數方程，獲得葉片結構及性能參數。對水平軸風力機來說，空氣流過葉輪時一方面沿主流方向流動，另一方面作與葉輪旋轉方向相反的圓周運動，同時由于葉片附近剪切流的作用，在葉片后方形成疊加于螺旋形流線上的渦旋運動。考慮到空氣流動沿主流方向和切線方向的動量損失，引入軸向誘導因子和切向誘導因子來計算葉間和葉片尾部氣流軸向和切向速度。關于應用葉素動量理論進行風力機葉片設計的計算步驟在許多文獻中均有所論述。葉片設計計算需要確定的參數包括葉片弦長、葉片流動角、葉片攻角、葉片扭轉角以及軸向和切向誘導因子等參數，它們在設計之初都是未知的，且相互影響。與一般工程設計類似，在開始設計時需要先假定一些幾何或結構參數，通過迭代或優化的過程獲得滿足設計性能要求的幾何參數。在現有文獻中，關于如何確定葉片有關幾何參數的初始分布介紹較少，本文在分析葉素動量理論實施步驟的基礎上上介紹幾種確定軸向誘導因子和切向誘導因子的方法以及確定葉片弦長的方法，進一步明確葉素動量理論的實現過程。

葉素動量理論的基本模型

葉素動量理論建立在葉素氣動理論和動量守恒原理的基礎上。葉素速度三角形和力矢量圖如圖1所示。

圖1中，D為阻力；L為升力；Fn為軸向力；Ft為切向力；V∞（1-a）為軸向速度；?r（1+b）為切向速度；V∞為風輪上游遠方風速；?為風輪旋轉角速度；W 為風輪處氣流相對速度；a 為軸向誘導因子；b 為切向誘導因子；α為攻角；β為扭轉角；φ為流動角。根據文獻，軸向誘導因子a 、切向誘導因子

b 分別由式（1）和式（2）定義。

式中，V 為葉間氣流軸向速度分量；ω為葉間氣流角速度，其方向與葉輪（或風輪）轉動方向相反。

根據動量守恒和動量矩守恒原理，氣流作用于葉素的推力（軸向力）和力矩可通過式（3）和式（4）表示。

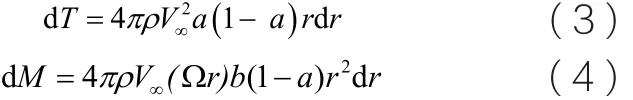
葉素單元效率ηr、當地風能利用系數dCP可表示為：

軸向誘導因子和切向誘導因子的關系式為：

圖1　典型葉素速度三角形和力矢量圖

式（8）和式（9）中，B為葉片個數；c為葉片弦長。分別聯立式（3）與式（8）及（4）與式（9），得到軸向誘導因子和切向誘導因子與葉片弦長、翼型氣動參數及流動角的關系式：

或

由式（10）和式（11）可進一步將軸向誘導因子和切向誘導因子寫成顯式的形式。若不計空氣阻力，則軸向誘導因子和切向誘導因子的關系式又可表示為：

式（3）—式（14）即為葉素動量理論的基本關系式。

葉素動量理論的實現方法

從式（10）—式（13）可知，葉素幾何參數、氣動參數及誘導因子互為函數關系，給方程的求解帶來一定困難，但是分析式（10）—式（13）并結合葉素速度三角形可一發現，翼型氣動參數是葉片設計的基礎數據，誘導因子是設計過程的中間參數，因此葉片設計可首先從翼型氣動參數入手。

攻角α的確定

葉素動量理論假定沿葉片徑向葉素氣動特性是獨立的，其氣動特性用翼型的氣動特性表示。翼型的氣動特性根據翼型實驗或計算獲得。升力系數CL和阻力系數CD分別是攻角α和雷諾數Re的函數，即：

雷諾數Re根據相對速度W 和弦長c 定義：

其中，ν為空氣運動粘度。

軸向誘導因子和切向誘導因子的確定

在簡化計算中，軸向誘導因子a 和切向誘導因子b可根據式（5）和式（7）或式（6）和式（14）來確定。

將式（5）和式（7）分別對切向誘導因子b求一階導數，并令其為零，可得：

以式（6）最大為目標函數，以式（14）為約束條件，通過求解這一約束優化優化問題便可得到軸向誘導因子a 和切向誘導因子b ，即：

以上兩種確定軸向誘導因子和切向誘導因子的方法都有一定的局限性，前者僅考慮了動量變化的因素，未考慮葉片氣動效應；后者優化模型的約束條件根據假設氣動阻力為零得出，因而兩者均不能保證同時滿足氣動力平衡及動量守恒的要求。

葉片初始幾何參數的確定

由圖1可知，流動角φ與攻角α和扭轉角β的關系為：

由速度三角形可得：

若已知軸向誘導因子和切向誘導因子，由式（22）可得流動角φ，根據最佳攻角αopt由式（21）便可得到扭轉角β。但最佳攻角αopt是Re的函數，Re又與弦長c有關。由此可知，如何確定弦長或弦長的分布成為需要解決的另一關鍵問題。若把獲得葉輪最大風能利用系數作為目標函數，弦長c、葉尖速比λtip的變化范圍作為約束條件，建立優化模型，即：

通過求解這一優化問題，便可獲得葉片的幾何參數及運行參數。但由于優化過程中，設計變量的取值是任意的，不能保證沿葉片展向弦長和扭轉角的連續性。

關于葉片弦長和扭轉角沿葉片展向的變化，文獻以不同的計算模型進行了介紹，文獻 將這些方法歸納為簡化圓盤理論設計模型（Betz模型）、Schmitz 設計模型、Glauert 設計模型以及Wilson 設計模型，并給出前三種模型的計算公式，文獻將基于式（19）、（20）的計算方法稱為Wilson設計模型。除Betz模型外，其他三種模型均考慮了渦流的影響，但認為翼型阻力對葉片結構影響較小，在計算弦長和扭轉角時略去了翼型阻力的影響。如文獻推導了不計翼型空氣阻力并假定軸向誘導因子和切向誘導因子按式（18）計算的情況下，流動角和葉片組合結構參數的分布的計算公式，由此可預測葉片弦長的分布。以最大風能利用系數為目標設計出的葉片，根部弦長往往很大，不易加工且增加葉片重量，因此需作修正，文獻 以采用NACA4412翼型設計出的葉片為例，認為可在葉片展向70%和90%處連線延伸葉片獲得統一錐度的葉片設計。文獻給出用線性和樣條函數修正葉片弦長的方法。文獻也指出，理想葉片的弦長和扭角沿展向呈非線性變化，葉根處的弦長及扭角均較大，需要對弦長和扭角進行修正。應用Schmitz 設計模型、Glauert 設計模型以及Wilson 設計模型計算葉片弦長時仍然要用到升力系數，在葉片弦長未知時，升力系數將無法確定，只能根據假設的雷諾數和攻角來確定，或采用理想流體繞流翼型時的升力系數。

從實用的角度出發，文獻 給出按指數規律分布的弦長計算式：

給定葉片葉根和葉尖的弦長后，根據式（25）可確定系數b1和指數b2。以Wilson 設計模型為基礎，考慮弦長修正，確定葉片根部和尖部弦長后根據式（25）可獲得具有較好性能的弦長分布。

圖2　葉片弦長分布

圖3　葉片扭轉角分布

圖4　葉素單元效率

計算實例

考慮一小型風力機，風力機功率為10kW，傳動裝置效率η=0.8，葉片數B=3，設計風速V∞=8m/s，初選風能利用系數CP=0.4。風輪直徑，風力機轉速按式（25）、（26）計算。葉尖：

速比λtip=7，確定葉根弦長、葉尖弦長分別為croot=0.65m、ctip=0.25m。葉片斷面翼型選為SG6043翼型。主要計算步驟如下：

1）應用式（25）計算葉片弦長分布；

2）采用XFOIL軟件或其它軟件計算不同雷諾數、不同攻角下翼型升力系數和阻力系數，找出每一雷諾數下最大升阻比對應的攻角，即αopt=fα（Re，εmax）；

3）應用迭代計算法，初設軸向誘導因子aold=1/3、切向誘導因子bold=0.1；

4）根據式（22）、（21）計算流動角和扭轉角；

5）根據式（10）、（11）得出更新的軸向誘導因子anew、切向誘導因子bnew；

6）計算軸向誘導因子和切向誘導因子差值：?a，?b，并判斷差值的絕對值是否小于給定的誤差限，若滿足則執行下一步，否則更新軸向誘導因子和切向誘導因子，轉第4）步；

7）根據式（5）、（6）計算葉素單元效率ηr、當地風能利用系數dCP，對dCP積分獲得風力機葉輪的風能利用系數CP。根據需要也可計算其他性能參數。

計算中，葉尖損失修正因子按文獻給出的公式計算。葉片弦長、扭轉角、葉素單元效率計算結果如圖2-圖4所示。

圖2所示葉片根部位于半徑比r/ R =0.05處，葉片根部與輪轂連接采用圓柱形過渡。由圖4可以看出，葉素單元效率最大值位于半徑比r/ R =0.8附近，最大值為0.54。葉輪風能利用系數為0.48，按此方法可使風輪獲得較高的性能。

結束語

葉素動量理論是風力機葉片設計實用的工程方法。空氣繞流葉片的運動是具有渦旋的復雜流動，通過引入軸向誘導因子和切向誘導因子反映氣流沿軸向和切向速度的變化，使基于動量守恒原理和氣動理論的分析方法成為可能。根據對渦流及誘導因子計算方法的不同形成不同的計算模型，在應用葉素動量理論設計葉片時，各種參數互相影響，但確定葉片各斷面合理的弦長是設計過程的重要環節，考慮到對理性情況下弦長的修正，采用多項式或指數規律變化的弦長分布可簡化計算過程并能獲得較高的風能利用系數。

10.3969/j.issn.1001- 8972.2016.18.029