時頻柵格誤差條件下的雙基地MIMO雷達角度估計

黃中瑞, 周青松, 張劍云

(電子工程學院, 安徽 合肥 230037)

?

時頻柵格誤差條件下的雙基地MIMO雷達角度估計

黃中瑞, 周青松, 張劍云

(電子工程學院, 安徽 合肥 230037)

研究了時頻柵格誤差引起的匹配濾波器失配下雙基地多輸入多輸出(multiple-inputmultiple-output,MIMO)雷達的角度估計問題。首先,建立了存在時延和多普勒頻率柵格誤差條件下的雙基地MIMO雷達信號模型;其次,推導了正交頻分復用線性調頻信號和相位編碼信號的柵格誤差失配矩陣,并分析了其對目標收發角度估計的影響;再次,針對正交頻分復用線性調頻信號,提出了平行因子和最小二乘相結合的發射角度估計算法,該方法能夠有效減小柵格誤差失配矩陣對發射角度估計的影響;最后,仿真實驗表明,柵格誤差失配矩陣對相位編碼信號的角度估計影響較小,但對正交頻分復用線性調頻信號的發射角度估計則會產生較大的影響,從而進一步驗證了理論分析的正確性。

雙基地多輸入多輸出雷達; 柵格誤差失配矩陣; 角度估計; 平行因子算法; 最小二乘算法

0　引　言

多輸入多輸出(multiple-inputmultiple-output,MIMO)雷達是近年來提出的一種新型體制雷達[1]。MIMO雷達的每個陣元可以獨立發射波形因而具有更高的自由度[2-4],同等陣元配置條件下與相控陣雷達相比,在目標檢測和參數估計方面具有更加優越的性能。MIMO雷達按照配置方式分為統計MIMO雷達和單(雙)基地其中雙基地MIMO雷達。統計MIMO雷達[5]的陣元空間分布較遠,能夠獲得空間分集增益,可有效提高對閃爍目標的檢測性能。單(雙)基地MIMO雷達[6]的收發陣元采用相干配置,能夠獲得波形分集增益,可有效改善目標參數的估計精度,提高最大可識別目標的數目。本文主要以雙基地MIMO雷達的角度估計為研究對象。

雙基地MIMO雷達的收發陣列是分開配置,兩者相對目標的視角可能相差很大,因而需要同時估計出目標的發射角度(directionofdeparture,DOD)和接收角(directionofarrival,DOA),另外還需考慮同一個目標收發角度的配對問題。文獻[7]基于Capon算法利用二維空間搜索方法實現了目標的收發角度聯合估計,但是該方法的缺點是計算量太大。文獻[8]將線性陣列的旋轉不變性(estimationofsignalparametersviarotationalinvariancetechniques,ESPRIT)算法擴展到了MIMO雷達的收發角度估計中,但需額外的配對算法。文獻[9-11]分別利用降維多重信號分類(multiplesignalclassification,MUSIC)、共軛ESPRIT和多項式求根方法對目標的收發角度進行了估計,進一步降低了算法的計算量。文獻[12]利用雙基地MIMO雷達接收數據的匹配輸出具有三面陣模型特性,基于平行因子(parallelfactor,PARAFAC)算法實現了運動目標收發角度和多普勒頻率的聯合估計,由于在迭代過程中能夠給出各個求解變量的最小二乘閉式表達解,因而具有較低的運算法復雜度,此外,該方法能夠實現收發角度的自動配對。文獻[13]在上述估計算法的基礎上,進一步考慮了陣列天線間存在互耦影響下的收發角度估計,利用循環算法實現了角度和互耦矩陣的迭代優化,但該方法的優化性能對初始點選擇十分敏感,致使算法的穩健性不佳。文獻[14]基于互耦矩陣的對稱Toeplitz結構,提取出收發旋轉不變因子,在得到收發角度的基礎上通過求解二次優化問題獲得了對互耦系數的估計值。

但是,上述文獻均沒考慮匹配濾波器失配情形下的雙基地MIMO雷達角度估計問題。在對目標角度估計之前,需要對MIMO雷達的接收數據進行匹配濾波,如果預先估計的目標時延和多普勒頻率與目標真實值并不精確相等,便會存在時延補償誤差和多普勒頻率補償誤差。這勢必造成目標角度信息畸變,如還用傳統方法對目標角度進行估計,其性能將急劇下降。所以研究匹配濾波器失配下的雙基地MIMO雷達角度估計是一個具有重要理論意義的課題。目前國內外僅有獻[15]對此問題進行了研究。文獻[15]建立了匹配濾波器失配下的信號模型,并通過仿真實驗分析了失配效應對模糊函數、波束形成以及角度估計的影響。遺憾的是該文并沒有從理論上分析失配效應對MIMO雷達參數估計的具體影響。

本文在文獻[15]的基礎上,考慮匹配濾波器的時延和多普勒頻率柵格誤差失配對目標角度估計的影響。首先,從理論上建立多目標不同時延和多普勒頻率柵格誤差情形下MIMO雷達的統一信號模型;其次以正交頻分復用線性調頻(orthogonalfrequencydivisionmultiplexinglinearfrequencymodulation,OFDM-LFM)信號和相位編碼(phasecoded,PC)信號為例,探討了柵格誤差失配矩陣對目標角度估計的影響,并且得到了此影響與MIMO雷達具體發射信號形式有關的結論;再次,提出一種平行因子-最小二乘(parallelfactor-leastsquares,PARAFAC-LS)算法對目標的發射角度進行估計,有效減小了發射信號為OFDM-LFM信號時,柵格誤差失配矩陣對目標發射角度估計的影響,而且所提方法能夠實現目標收發角度的自動配對。

1　MIMO雷達信號模型

考慮一雙基地MIMO雷達,其發射陣列和接收陣列均為均勻線陣,陣元數分別為M和N,陣元間距分別為dt,dr,陣列配置如圖1所示。為討論方便,假設dt=dr=λ/2(λ為波長)。發射、接收陣列之間的基線距離為D,且D?λ。在空間遠場同一距離單元內存在P個互不相關的目標,相應的發射、接收角分別記為φp與θp,其中-π/2≤θp,φp≤π/2, p=1,2,…,P。第m發射陣元歸一化基帶發射波形為sm(t),且不同發射信號之間近似滿足正交特性,即

其中,T為基帶波形的脈沖寬度,脈沖重復周期為Tr,則發射信號矩陣為S(t)=[s1(t),s2(t),…,sM(t)]T,(·)T表示向量(矩陣)的轉置,(·)*表示向量(矩陣)的共軛。

圖1　雙基地MIMO雷達收發陣元配置圖Fig.1　Schematic diagram of bistatic MIMO radar

其中發射陣元數目為M,接收陣元數目為,P個目標情況下,t時刻,N個接收陣元接收到第個脈沖的回波信號為

(1)

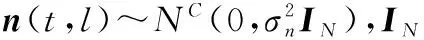
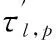
(2)

根據式(2)可得匹配濾波器組的輸出為

(3)

式中,(·)H表示向量(矩陣)的共軛轉置。

令

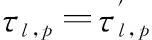
(4)

同時為了簡化討論,仍然假設發射信號近似滿足正交性,因而Cp為一個對角陣,將式(4)代入式(3)可得:

(5)

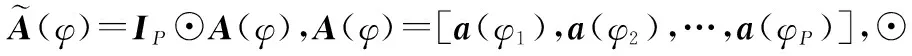
根據式(5)可知,柵格誤差失配矩陣C會導致發射導向矢量產生畸變,從而使發射角度估計產生偏差,所以對C進行分析并尋找相應的發射角度校正算法是一個亟待解決的問題。

2　柵格誤差失配矩陣對發射角度估計的影響

由文獻[15]可知,不同形式的發射信號其量化失配誤差矩陣也是不一樣的,本文主要以OFDM-LFM信號和正交多相位碼(polyphase orthogonal code,PC)信號為例,分析柵格誤差失配矩陣對發射角度的影響。

2.1OFDM-LFM信號的柵格誤差失配矩陣分析及其對發射角度估計的影響

假設MIMO雷達在發射端發射OFDM-LFM信號,即每個陣元發射一個窄帶的線性調頻信號,不同陣元發射的線性調頻信號的中心頻率不同。各個陣元的發射信號分別為

(6)

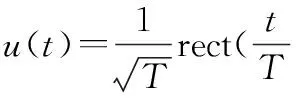
Cp=diag(cp)

(7)

式中,cp=[cp,1,cp,2,…,cp,M]T,此時,MIMO雷達的多普勒頻率敏感問題與普通相位編碼雷達類似的是,目標多普勒頻率和時延誤差影響了各個陣元發射信號與其回波信號間的相關性;不同的是,普通相位編碼雷達的這種影響在數學上可以歸結為一個復數加權,而MIMO雷達則為一個復數對角陣;所以兩種影響對目標角度估計來說是有本質區別的,具體分析第p個目標的柵格誤差失配矩陣的第m個對角元素為

(8)

式中

(9)

將式(8)和式(9)代入式(7)可得

(10)

由式(8)和式(9)可知,柵格誤差失配矩陣對目標角度估計的影響主要表現在兩個方面:一方面，隨著時延和多普勒頻率柵格誤差的增大,γp的模值將會逐漸減小,致使接收信號的信噪比降低,從而在一定程度上影響目標收發角度的估計精度,本文將γp稱為OFDM-LFM信號的信噪比損失因子;另一方面，柵格誤差失配矩陣是一個對角陣,但是對角線各個元素的相位存在一個固定差值,因而相當于對發射導向矢量的各元素進行了不同的相位加權,致使發射導向矢量產生畸變,從而影響目標發射角度的估計性能,但對接收角度無影響。

進一步給出第p個目標受失配矩陣扭曲的發射導向矢量為

(11)

從式(11)可知,失配矩陣對發射導向矢量的各個元素附加了一個新的相位,附加相位的增量與標號km∈[0,1,…,M-1],m=1,2,…,M有關,當km與陣元標號同步變化時,不同陣元間的時延柵格誤差引起的相位差增量與波程差的相位增量變化一致,這種耦合致使扭曲導向矢量仍然具有旋轉不變特性,不過其對應的角度已不是目標的真實角度,對于這種耦合一般的算法難以解決。當km與陣元標號異步變化時,不同陣元間的時延柵格誤差引起的相位差增量與波程差相位增量變化也不一致,對于這類問題的角度估計可以采用平行因子分析和最小二乘相結合(PARAFAC-LS)算法進行解決,本文將在第3節對這個問題進行深入研究。

2.2PC信號的柵格誤差失配矩陣分析及其對發射角度估計的影響

第2.1節推導了OFDM-LFM信號的柵格誤差失配矩陣,并從理論上分析了其對發射角度估計的影響,本節在此基礎上進一步分析PC信號的柵格誤差失配矩陣及其對發射角度估計的影響。假設MIMO雷達的發射信號為相位編碼信號,發射陣元數為M,每個陣元發射信號的編碼長度為L,第m個陣元發射信號的復包絡可以表示為

(12)

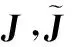
(13)

式中，IL為L維方陣。同時定義M維的方陣Zp,q,其中第(p,q)個元素為1,其余元素為0,則

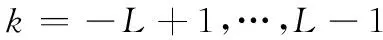
(14)

式中,?為Kronecker積；Jp,q,k為LM維的方陣。

根據式(13)和式(14)可將發射信號的非周期自相關和互相關函數表示成向量相乘的形式

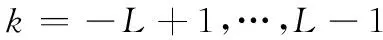
(15)

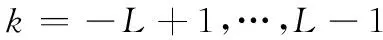
(16)

假設所采用的相位編碼信號近似滿足正交性,即

(17)

由于相位編碼信號是時域正交信號,各個陣元的信號帶寬近似一致,可視為一個窄帶系統,因而采用臨界采樣率對接收信號進行離散化,亦即采樣間隔為發射信號的子碼寬度τs。為了討論的方便,以第p個目標為例進行分析,結合式(4)和式(15)可以給出第p個目標的柵格誤差失配矩陣的第m個對角元素為

(18)

式中,S′=S°Ω,Ω=[1,e-j2πΔfd,pτs,…,e-j2πΔfd,p(L-1)τs,…,1,…,e-j2πΔfd,p(L-1)τs]T,“°”為點乘。根據式(18)可得第p個目標的PC信號柵格誤差失配矩陣為

(19)

由于PC信號的柵格誤差失配矩陣是一個加權的單位陣,因而其對發射導向矢量各個元素的相位進行同一加權,故不會影響發射導向矢量的旋轉不變性,但是當存在多普勒頻率柵格誤差時,κp的模值會小于1,致使接收信噪比的下降,從而導致目標收發角度估計性能的下降,本文將κp稱為PC信號的信噪比損失因子。

3　基于PARAFAC-LS的多目標收發角度估計

對于角度估計來說,柵格誤差失配矩陣把發射陣元的導向矢量進行了線性組合,特別是對OFDM-LFM信號而言,其導向矢量已不再具有與真實目標位置一一對應的旋轉不變性。傳統的MUSIC算法和ESPRIT算法已無法對目標角度進行精確估計,為避免此失配矩陣對目標角度(特別是發射角度)估計的影響,本文采用PARAFAC-LS算法對此問題進行解決。需要說明的是,雖然下文方法主要針對OFDM-LFM信號提出,但是對PC信號的角度估計同樣適用。

3.1基于PARAFAC的收發角度導向矢量估計

式(5)給出了第個脈沖回波信號的匹配輸出,對其按列拉直可得:

(20)

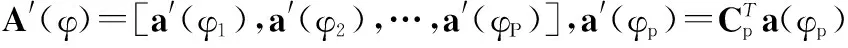
結合式(20)可以得到L個脈沖接收回波信號的匹配濾波輸出為

(21)

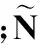
(22)

獲得張量χ的3個LMV縱向展開表達式后,利用交替迭代最小二乘(trilinearalternatingleastsquares,TALS)算法對等效發射矩陣A′(φ)和接收矩陣B(θ)進行估計,考慮到篇幅的限制本文不再對張量χ滿足典范/平行因子(candecomp/parafac,CP)分解的唯一性進行證明,直接給出給出TALS迭代流程:

步驟 1根據式(21)推導出三階張量χ沿收發角度方向上LMV縱向展開矩陣,如式(22)所示。

步驟 2給出因子數P和誤差門限ε>0。

(23)

(24)

(25)

(26)

(27)

(28)

(29)

由于柵格誤差失配矩陣對接收導向矢量的相位因子沒有影響,因而可以直接根據接收導向矢量的估計值對接收角度進行估計:

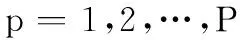
(30)

式中,angle(·)表示取相位操作。對目標的發射角度而言,柵格誤差失配矩陣對目標真實發射角度對應的導向矢量進行了改變,因而無法采用類似式(30)的方法進行估計。

3.2基于LS的目標發射角度估計

(31)

(32)

只要MIMO雷達陣元發射的OFDM-LFM信號的頻率步進值不隨陣元標號依次遞增(減),則T便為列滿秩矩陣,故可以得到式(32)的閉式LS估計為

(33)

根據式(33)可求得第p個目標的發射角度的估計值為

(34)

按照式(31)～式(34)對所有發射導向矢量進行計算,便可求得所有目標的發射角度,需要說明的是:利用PARAFAC估計出的收發導向矢量和目標具有一一對應的關系,因而基于PARAFAC-LS算法求得的目標收發角度能夠實現自動配對。

4　仿真實驗

假設雙基地MIMO雷達的發射陣列和接收陣列均采用線性配置,陣元間距均為半波長,發射陣元數目M=10,接收陣元數目(φ2,θ2)=(4°,2°),為了表述方便,將受柵格誤差失配矩陣影響的目標收發角度估計記為W-DOA和W-DOD,理想匹配濾波下目標收發角度估計記為B-DOA和B-DOD,存在柵格誤差失配矩陣時,利用本文算法估計的目標收發角度估計記為J-DOA和J-DOD,分別給出如下仿真實驗。

實驗 1柵格誤差失配矩陣對目標角度估計影響的性能分析

MIMO雷達分別發射OFDM-LFM信號和PC信號,參數分別設置如下:OFDM-LFM信號,各個陣元的碼元寬度為20μs,碼元內線性調頻信號的調頻斜率為5×1010,不同陣元的頻率步進間隔為1MHz,兩個目標的時延和多普勒頻率柵格誤差分別為0.5μs和50Hz,信噪比為10dB,各個陣元的頻率步進倍數分別為[0,1,2,3,4,9,8,7,6,5];PC信號,各個陣元的碼長為64,子碼寬度為1μs,兩個目標的時延和多普勒頻率柵格誤差分別為0.5μs和50Hz,信噪比為10dB,角度估計算法均為MUSIC算法,空間遠場存在兩個不相干的目標,其收發角度分別為(φ1,θ1)=(-3°,-2°)和(φ2,θ2)=(5°,3°),發射脈沖的個數為100。

圖2和圖3分別給出了雙基地MIMO雷達發射信號分別為PC信號和OFDM-LFM信號時,MUSIC算法的三維譜估計圖。

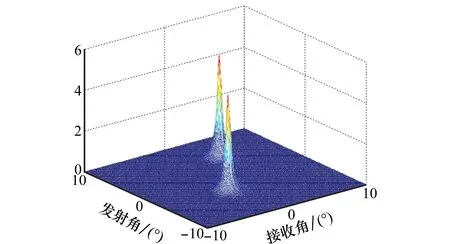
圖2　PC信號MUSIC算法的三維譜估計圖Fig.2　Estimation of the three-dimensional spectrum via MUSIC method of PC signal

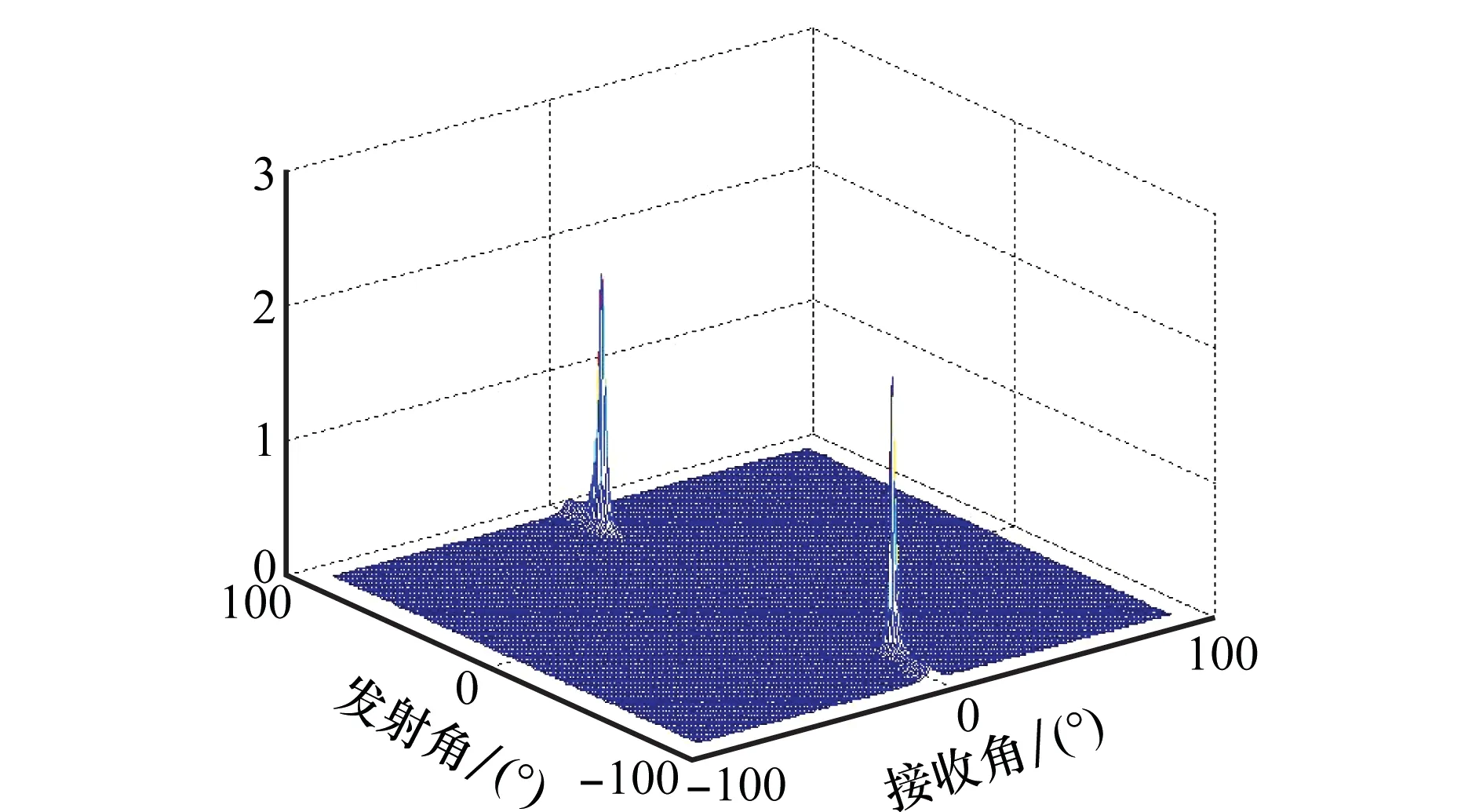
圖3　OFDM-LFM信號MUSIC算法的三維譜估計圖Fig.3　Estimation of the three-dimensional spectrum via MUSIC method of PC signal

從圖2和圖3可知,在時延和多普勒頻率柵格誤差相同的條件下,發射信號為PC信號時,利用MUSIC算法能夠精確的估計出兩個不相干目標的收發角度,而當發射信號為OFDM-LFM信號時,則無法準確估計出目標角度,其誤差集中體現在對目標的發射角度估計上,這與理論分析是一致的,即:①柵格誤差失配矩陣對目標角度估計的影響與MIMO雷達發射信號的具體形式有關;②柵格誤差失配矩陣對目標角度估計的影響主要體現在兩個方面,一是隨著時延和多普勒頻率柵格誤差的增大,OFDM-LFM信號的信噪比損失因子模值逐漸變小,如圖4所示,降低了接收信號的信噪比,使得目標收發角度估計的性能惡化;另一方面,柵格誤差失配矩陣對目標的發射導向矢量進行了加權,破壞了其與目標真實角度之間的一一對應性,因而對目標的發射角度估計產生了嚴重的影響。

圖4　OFDM-LFM信號信噪比損失因子隨時延補償誤差變化圖Fig.4　SNR loss factor of OFDM-LFM signal versus time-delay compensation error

從圖4可知,在時延補償誤差小于0.1μs時,信噪比損失因子均在0.95以上,隨著時延補償誤差的進一步降低,信噪比損失因子則迅速下降,當時延補償誤差為0.5μs時,信噪比損失因子為0.65左右,也就是說,當時延和多普勒頻率柵格誤差較小時,信噪比損失因子對接收信號信噪比的降低可以忽略不計,此時導致圖3中發射角度估計性能惡化的主要原因是,時延補償誤差引起的相位變化對發射導向矢量的各個相位進行了不同的疊加,致使其不在具有與真實角度一一對應的旋轉不變性。

圖5和圖6進一步分析了時延補償誤差變化對發射角度估計的影響,其中,信噪比為20dB,其收發角度分別為(φ1,θ1)=(-6°,-4°)和(φ2,θ2)=(-2°,-1°),發射脈沖的個數為100,兩個目標的時延和多普勒頻率柵格誤差分別為[0.001μs,0.1μs]和100Hz,其余仿真條件不變。

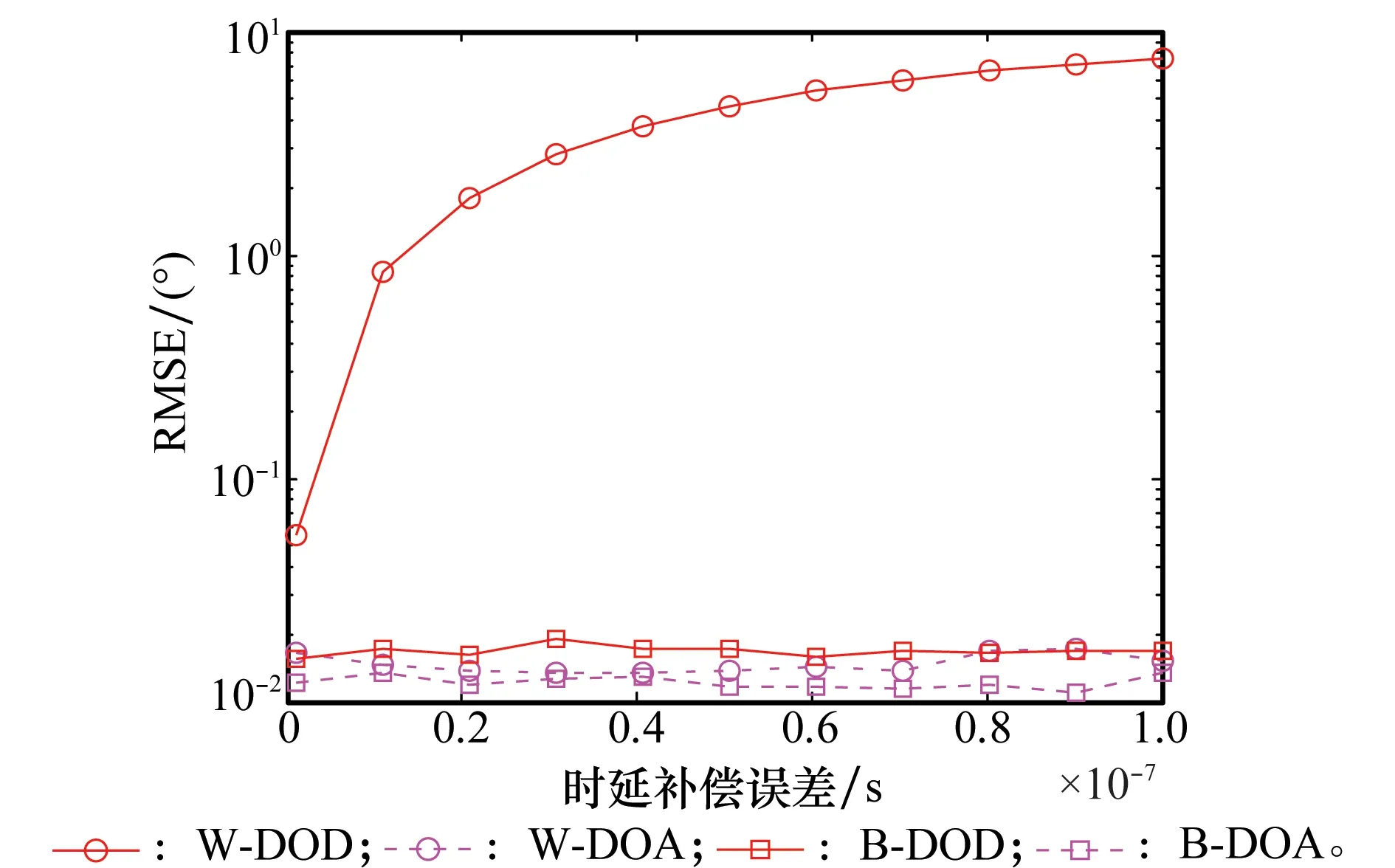
圖5　目標1角度估計性能隨時延補償誤差變化Fig.5　Performance of the angles of the target 1 　versus time-delay compensation error

由圖5和圖6可知,隨著時延補償誤差的增加,目標接收角度的估計性能只是略微下降,其原因是受到信噪比損失因子的影響,這與圖4的結論是一致的。而目標的發射角度估計性能隨著時延補償誤差的增加將極具惡化,主要原因是柵格誤差失配矩陣對發射導向矢量進行了改變,特別是在時延補償誤差較大時,將無法準確對目標的方向進行定位,因而給出一種能夠克服這種影響的角度估計算法是一個亟待解決的問題。

圖6　目標2角度估計性能隨時延補償誤差變化Fig.6　Performance of the angles of the target 2 　versus time-delay compensation error

實驗 2基于PARAFAC-LS算法的角度估計

本節對文中提出的PARAFAC-LS算法對目標收發角度估計的有效性能進行仿真實驗,以進一步說明所提方法的正確性,仿真條件同實驗1,蒙特卡羅實驗次數為100次。

圖7～圖9分別給出了不同條件下目標收發角度估計的星座圖,其中,+表示真實的目標位置。比較圖8和圖9可知,存在柵格誤差失配矩陣時,利用傳統的PARAFAC算法無法對目標的角度進行精確估計,而角度偏差主要體現在目標的發射角度估計上,而利用本文提出的PARAFAC-LS算法則能有效克服柵格誤差失配矩陣對發射角度估計的影響。比較圖7和圖8可知,雖然采用本文算法能夠對目標的角度進行估計,但是其估計精度與匹配濾波器理想匹配時相比,有一定程度的下降,這是因為時延和多普勒頻率柵格誤差影響了接收信號的信噪比,同等實驗條件下相當于降低了發射信號的能量。圖10和圖11進一步仿真了收發角度估計的均方根誤差(root-mean-squareerror,RMSE)隨信噪比的變化,其中,信噪比的變化范圍為[-40dB,20dB],其余仿真條件不變。

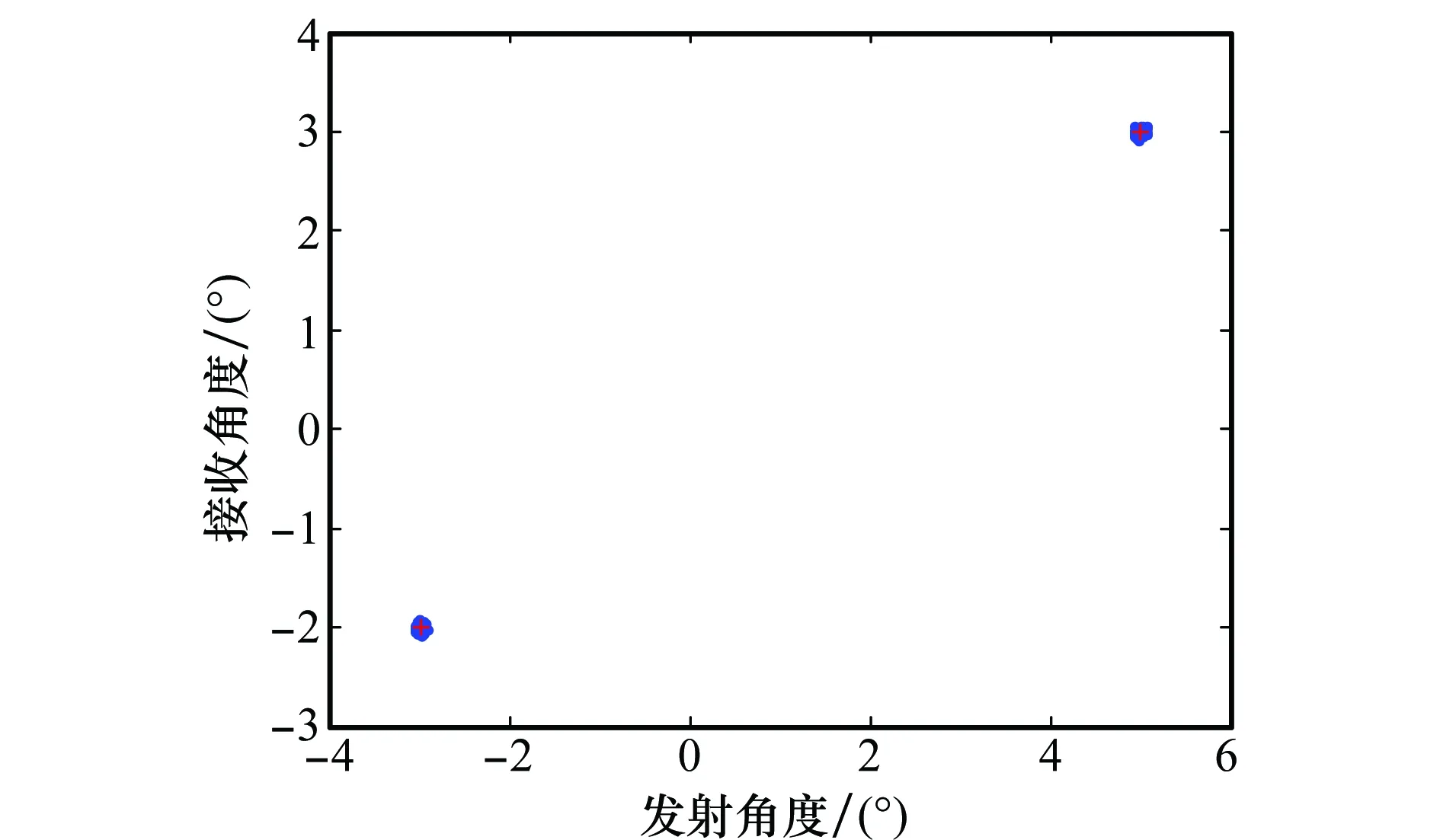
圖7　匹配濾波器理想匹配時角度估計的星座圖Fig.7　Constellation of the angles under the matching filter

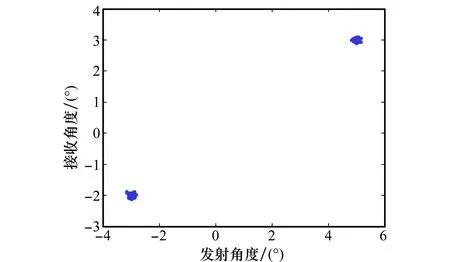
圖8　存在柵格誤差失配矩陣時基于本文算法的角度估計星座圖Fig.8　Constellation of the angles based on the proposed method with the grid error mismatch matrix

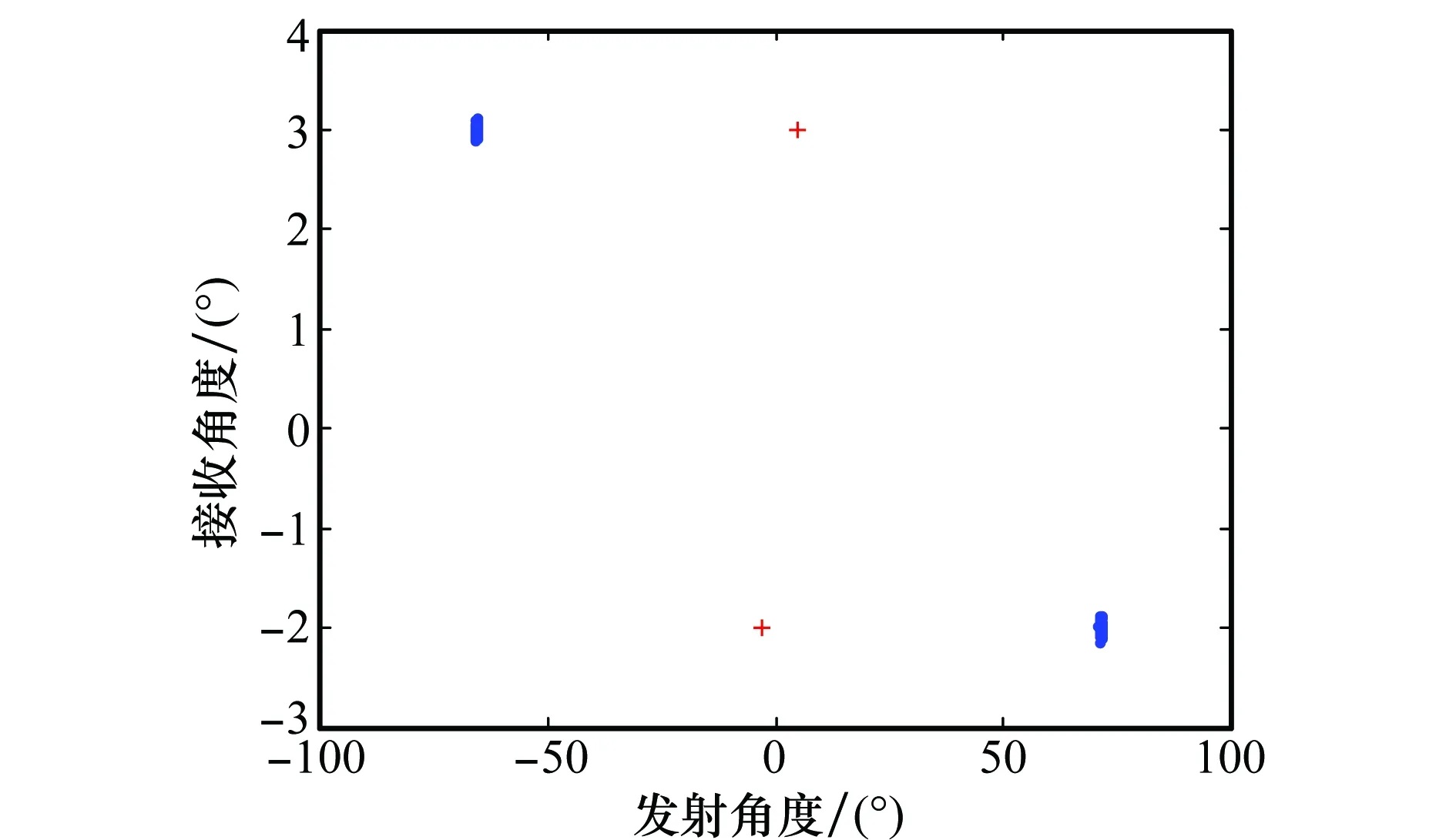
圖9　存在柵格誤差失配矩陣時文獻[12]算法的角度估計星座圖Fig.9　Constellation of the angles based on the reference 12 method with the grid error mismatch matrix

圖10和圖11分別給出了空間兩個不相干目標收發角度估計RMSE隨信噪比的變化圖,從中可知,在各個不同信噪比條件下,利用本文所提PARAFAC-LS算法估計出的目標收發角度均能獲得相對較好地RMSE,并且隨著信噪比的增加RMSE依次減小,這與匹配濾波器理想匹配時是一致的,也進一步說明了所提方法能夠有效解決柵格誤差失配矩陣對目標發射角度估計產生的影響。

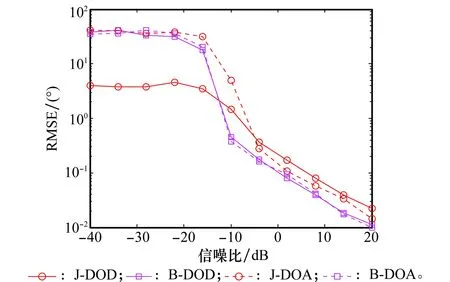
圖10　目標1收發角度估計RMSE隨信噪比變化Fig.10　RMSEs of the angles of the target 1 versus SNR

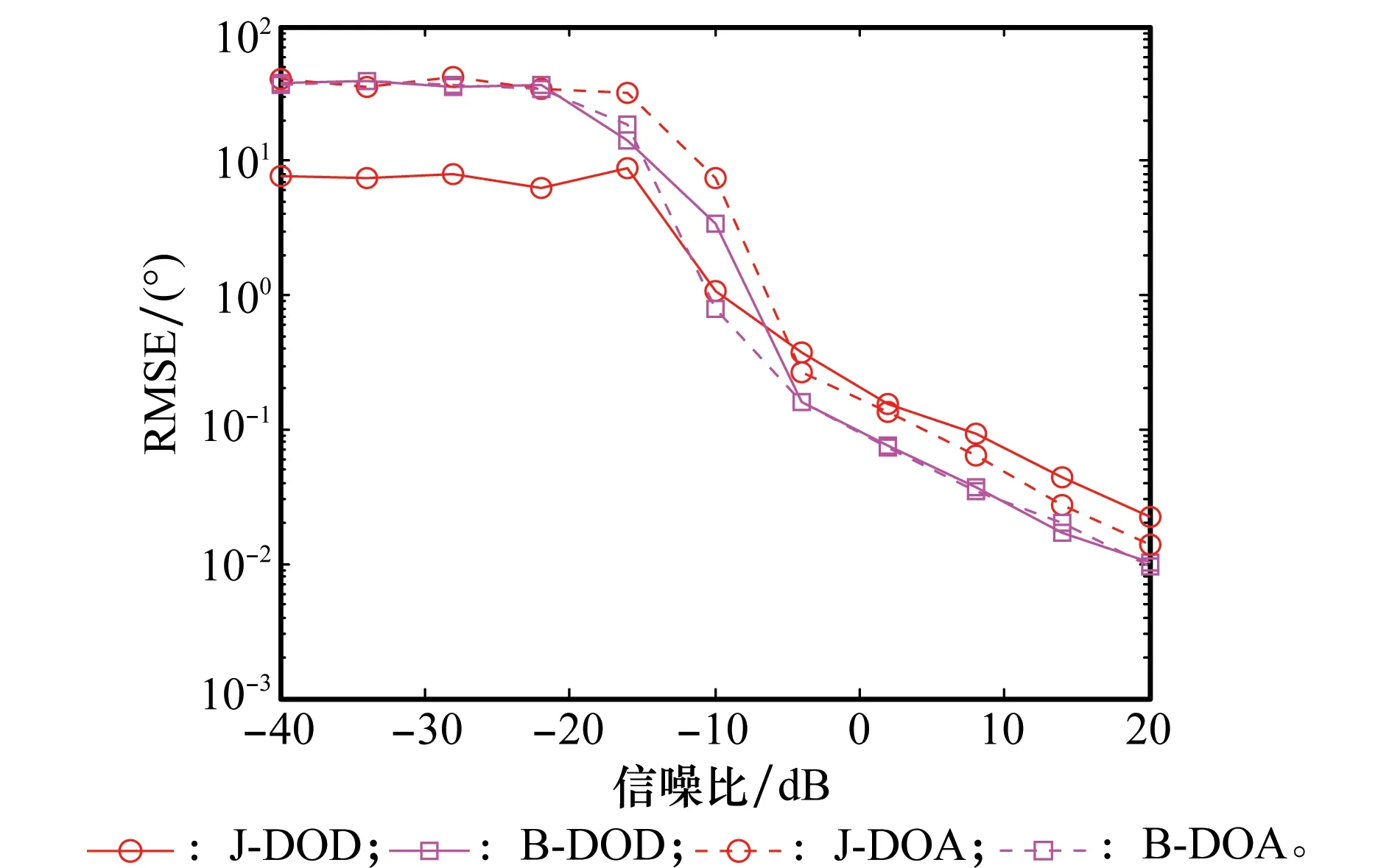
圖11　目標2收發角度估計RMSE隨信噪比變化Fig.11　RMSEs of the angles of the target 2 versus SNR

5　結束語

針對MIMO雷達匹配濾波器在實際中不能進行理想匹配的情況,分析了時延和多普勒頻率柵格誤差對目標收發角度估計的影響。首先,建立了存在時延和多普勒頻率柵格誤差時MIMO雷達的接收信號模型;其次,分別以OFDM-LFM信號和PC信號為例,從理論上推導了兩種信號匹配濾波時的柵格誤差失配矩陣,并在此基礎上分析了其對目標收發角度估計的影響,研究表明:柵格誤差失配矩陣對PC和OFDM-LFM信號都會造成接收信號信噪比的下降,從而對目標的收發角度估計性能產生一定的影響,但在時延和多普勒頻率柵格誤差較小時,這種影響可以忽略。特別是對于OFDM-LFM信號,柵格誤差失配矩陣會造成目標發射導向矢量的畸變,使其不再具有與真實目標一一對應的旋轉不變性,因而會對目標發射角度的估計產生嚴重影響;再次,為了克服OFDM-LFM信號柵格誤差失配矩陣對目標發射角度產生的影響,提出了PARAFAC-LS角度估計算法,該方法基于接收信號具有的三面陣特性,先利用PARAFAC算法估計出目標的接收角度和發射導向矢量,然后利用LS算法對目標的發射角度進行估計,從而有效避免柵格誤差失配矩陣對發射導向矢量產生的畸變;最后,仿真實驗驗證了理論分析的正確性。

[1]GuangH,AbeysekeraSS.ReceiverdesignforrangeandDopplersidelobesuppressionusingMIMOandphased-arrayradar[J].IEEE Trans.on Signal Processing, 2013, 61(6): 1315-1326.

[2]ZhangXY,LiaoGS,XuJW,etal.WaveformdesignforMIMOradartoimprovetargetdetectionandparameterestimation[J].Systems Engineering and Electronics, 2014, 36(8): 1494-1499.(張向陽,廖桂生,許京偉,等.提高MIMO雷達檢測和參數估計性能的波形設計[J].系統工程與電子技術,2014,36(8):1494-1499.)

[3]YangL,HuWJ,HeXD,etal.ModifiedPTSalgorithmcombiningtimeandspacedomainsignalprocessinginMIMO-OFDMsystem[J].Systems Engineering and Electronics, 2014, 36(12): 2526-2532.(楊霖, 胡武君, 何向東,等.MIMO-OFDM系統中聯合時域和空間域信號處理的改進PTS算法[J].系統工程與電子技術,2014,36(12):2526-2532.)

[4]HassanienA,VorobyovSA.Phased-MIMOradar:atradeoffbetweenphase-arrayandMIMOradars[J].IEEE trans. on signal processing, 2010, 58(6): 3137-3151.

[5]FisherE,HaimovichA,BlumRS,etal.Spatialdiversityinradar-modelsanddetectionperformance[J].IEEE Trans.on Signal Process, 2006, 54 (3):823-838.

[6]ChenJL,ZhuYP,GuH,etal.HighspeedmovingtargetlocalizationmethodforbistaticMIMOradar[J].Systems Engineering and Electronics, 2013, 35 (5): 962-967.(陳金立, 朱艷萍, 顧紅，等.雙基地MIMO雷達的高速運動目標定位方法[J].系統工程與電子技術, 2013, 35 (5): 962-967.)

[7]YanH,LiJ,LiaoG.MultitargetidentificationandlocalizationusingbistaticMIMOradarsystem[J].EURASIP Journal on Advance in Signal Process, 2008, 8 (2): 1-8.

[8]ChenDF,ChenBX,QinGD.AngleestimationusingESPRITinMIMOradar[J].IEE Electronics Letters,2008,44(12):770-771.

[9]ZhangXF,XuLY,XuL,etal.directionofdeparture(DOD)anddirectionofarrival(DOA)estimationinMIMOradarwithreduced-dimensionMUSIC[J].IEEE Communications Letters, 2010, 14 (12): 1161-1163.

[10]YangML,ChenBX,YangXY.ConjugateESPRITalgorithmforbistaticMIMOradar[J].IEEE Electronics Letters, 2010, 46 (25): 1692-1694.

[11]XieR,LiuZ.Multi-targetlocalizationbasedonpolynomialrootingforbistaticMIMOradar[J].Journal of Electronics and Information Technology, 2010, 32 (9): 2197-2220.(謝榮, 劉崢. 基于多項式求根的雙基地MIMO雷達多目標定位方法[J].電子與信息學報, 2010, 32 (9): 2197-2220.)

[12]ZhangJY,ZhengZD,LiXB.AnalgorithmforDOD-DOAandDopplerfrequencyjointlyestimatingofbistaticMIMOradar[J].Journal of Electronics & Information Technology, 2010, 32(8): 1843-1848.(張劍云, 鄭志東, 李小波. 雙基地MIMO雷達收發角及多普勒頻率的聯合估計算法[J].電子與信息學報, 2010, 32(8): 1843-1848.)

[13]LiuZG,LiaoGS.MutualcouplingcalibrationforbistaticMIMOradarsystems[J].Chinese Journal of radio science, 2010, 25 (4): 663-667.(劉志國, 廖桂生. 雙基地MIMO雷達互耦校正[J].電波科學學報, 2010, 25 (4): 663-667.)

[14]ZhengZZ,ZhangJY,KangK,etal.JointDODandDOAestimationforbistaticMIMOradarinthepresenceofmutualcoupling[J].Scientia Sinica Informations, 2013, 43(6): 784-797.(鄭志東, 張劍云, 康凱，等. 互耦條件下雙基地MIMO雷達的收發角度估計[J].中國科學: 信息科學, 2013, 43(6): 784-797.)

[15]BenjaminF.EffectsofmodelmismatchinMIMORadar[J].IEEE Trans.on Signal Processing, 2012, 60(4): 2071-2076.

Angle estimation of bistatic MIMO radar under the time frequency grid error

HUANG Zhong-rui, ZHOU Qing-song, ZHANG Jian-yun

(Electronic Engineering Institute, Hefei 230037, China)

Theangleestimationforbistaticmultiple-inputmultiple-output(MIMO)radarunderthemismatchfilterinthepresenceoftimefrequencygriderrorisstudied.Firstly,thesignalmodelforbistaticMIMOradarunderdelayandDopplerfrequencygriderrorisbuilt.Secondly,thegriderrormismatchmatrixoforthogonalfrequencydivisionmultiplexinglinearfrequencymodulationsignalandphasecodedsignalareconstructedandtheeffectitpayontheangleestimationareanalyzed.Furthermore,theparallelfactoranalysisandtheleastsquaresmethodarecombinedtoestimatethetransmitanglefortheorthogonalfrequencydivisionmultiplexinglinearfrequencymodulationsignal.Theeffectonthetransmitangleestimationcausedbythegriderrormismatchmatrixcanbereducedbyusingtheproposemethod.Finally,simulationresultsdemonstratethat,theimpactofthegriderrormismatchmatrixontheangleestimationinphasecodedsignalislittle,butfortheorthogonalfrequencydivisionmultiplexinglinearfrequencymodulationsignalisinreverse,whichillustratesthevalidityofthetheoryanalysis.

bistaticmultiple-inputmultiple-output(MIMO)radar;griderrormismatchmatrix;angleestimation;parallelfactormethod;leastsquaresmethod

2015-08-06；

2016-01-25；網絡優先出版日期：2016-05-03。

國家自然科學基金(61201279)；安徽省自然科學基金(1408085MF128)資助課題

TN958

ADOI:10.3969/j.issn.1001-506X.2016.10.07

黃中瑞(1988-),男,講師，博士,主要研究方向為陣列信號處理、MIMO雷達信號處理。

E-mail:18756073857@163.com

周青松(1982-),男,講師,博士,主要研究方向為高速數字信號處理、凸優化理論。

E-mail:Zhouqingsong1207@gmail.com

張劍云(1963-),男,教授,博士,主要研究方向為雷達及目標環境模擬、雷達信號處理、高速信號處理。

E-mail:jyzh@vip.sina.com

網絡優先出版地址：http://www.cnki.net/kcms/detail/11.2422.TN.20160503.0945.004.html