一種適用于紅外制導彈藥的偏置比例導引律
王廣帥, 林德福, 范世鵬, 臧路堯
(1. 北京理工大學宇航學院, 北京 100081; 2. 北京航天自動控制研究所, 北京 100854)
?
一種適用于紅外制導彈藥的偏置比例導引律
王廣帥1, 林德福1, 范世鵬2, 臧路堯1
(1. 北京理工大學宇航學院, 北京 100081; 2. 北京航天自動控制研究所, 北京 100854)
針對彈道成型制導律不適用于紅外制導彈藥的落角約束,提出了一種無需剩余飛行時間信息的偏置比例導引律。根據建立的彈目相對運動幾何模型和碰撞三角形,推導出了期望落角與需用偏置積分量之間的函數關系;求出了偏置比例導引無量綱彈道閉環解與穩定域,并分析了不同因素對偏置比例導引律制導性能的影響;最后對比研究了偏置比例導引制導律與彈道成型的性能。仿真結果表明,偏置比例導引律在落角精度、制導精度與最大需用過載這些關鍵制導性能指標方面接近于彈道成型制導律,適用于紅外制導彈藥對地面運動裝甲目標的落角約束問題。
彈道成型制導律; 紅外制導彈藥; 偏置比例導引律; 落角約束
0 引 言
紅外成像制導由于其靈敏度高、具備多目標鑒別能力和抗干擾能力強等特性,成為新一代反坦克導彈的一種主要制導方式[1-2]。例如,歐洲“崔格特”和美國“標槍”反坦克導彈均采用紅外凝視成像制導技術,具有“發射后不用管”能力[3]。為提高對運動裝甲目標的毀傷概率,紅外反坦克導彈多采用掠飛攻頂方式來打擊坦克裝甲最薄弱的頂部,這就要求制導律在保證目標命中的基礎上,同時實現落角約束[4]。
工程中增大落角最直接的方式就是在制導律中加入過重力補償,文獻[5]采用了帶過重力補償的比例導引來增大落角。但由于重力補償系數與落角之間不存在直接對應的函數關系,因此難以實現對落角大小的精確控制。
國內外關于落角約束制導律的理論研究較多。最有代表性的是基于落角約束的最優制導律,實現落角約束的同時使得控制能量需求最小。文獻[6]以“導彈過載平方的積分”為目標函數,從最優控制理論出發推導出了最優制導律,文獻[7-9]以此為基礎研究了相關擴展形式的最優制導律;以Zarchan為代表的學者從數學上Schwartz不等式出發,采用相同的目標函數推導出了相同形式的最優制導律—彈道成型[10-11]。國內學者將目標函數擴展為包含有剩余飛行時間冪函數,推導出末端過載為零的擴展彈道成型制導律,并對其性能進行了全面研究[13-15]。另外,在傳統比例導引基礎上加時變偏置項構成偏置比例導引律也是一種實現落角約束的方法,文獻[15]加了一個與剩余飛行時間成函數關系的偏置項來構成偏置比例導引律,并且推導出了它的最優形式。
上述這些最優制導律實現落角精確控制的過程中均離不開當前剩余飛行時間信息,剩余飛行時間根據當前彈目距離來計算獲得。由于紅外導引頭不像雷達導引頭那樣可以直接測量彈目距離,而只能通過在彈體上額外增加慣導組件或GPS制導模塊來間接計算彈目距離,因此紅外制導彈藥采用最優制導律時就產生了額外的硬件需求問題。
本文在文獻[16-17]提出的一種無需剩余飛行時間偏置比例導引律的基礎上,進一步研究了這種制導律的無量綱解析解和穩定域,并將其應用于紅外制導武器對地面慢速運動目標的落角約束中,在實現落角精確控制的同時避免了紅外制導彈約的硬件額外需求問題。通過仿真,將這種偏置比例導引律與彈道成型制導律的制導性能進行了對比研究。
1 彈目相對運動模型
紅外制導彈藥打擊地面慢速運動目標時彈目相對運動可分解為俯仰和偏航兩個平面上的運動,鑒于二者沒有本質區別,只研究俯仰平面的相對運動,幾何關系如圖1所示。
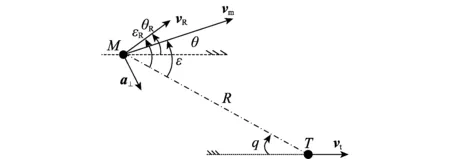
圖1 彈目相對運動幾何關系圖Fig.1 Relative motion geometry between missile and target
圖1中,M和T分別表示導彈與目標位置;R表示彈目距離;vt表示目標速度矢量;vm、ε、θ分別表示導彈的速度矢量、目標視角和速度傾角;vR、εR、θR分別表示相對速度的矢量、方向角和傾角。假設逆時針方向作為角度的正方向,則彈目相對運動微分方程組可表示為
(1)
彈道終端的彈體速度矢量vm,f、目標速度矢量vt和相對速度矢量vR,f組成了彈目碰撞三角形,如圖2所示。um,f、ut、uR,f分別表示上述3個速度的單位矢量;θf、θR,f、Δθ分別表示碰撞時刻彈體終端落角、彈目相對速度傾角和彈體速度矢量與相對速度矢量間的夾角。

圖2 彈目碰撞三角形Fig.2 Collision triangle between missile and target
分析碰撞三角形可得
(2)
根據三角形正弦定理得到速度夾角
(3)
導彈速度遠大于目標速度,使得彈體速度與相對速度夾角為小量,故有
(4)
式(4)代入式(2)得到
(5)
考慮到彈體過載沿彈體速度法向,忽略重力和阻力,彈體速度vm是常值;相對速度vR是變量,采用余弦定理得到彈道終端相對速度:
(6)
式中,vt,f為彈道末端目標速度。令目標速度與導彈速度之比為
(7)
式(6)、式(7)代入式(5)得
(8)
同理,可得到初始時刻速度夾角為
(9)
由于k為小量,且其數值大小對相對速度傾角的計算影響較小,所以工程中可對k取常值,并根據目標類型提前裝訂;彈體初始速度傾角θi則可由載機外部傳輸或地面初始對準獲取。
2 落角約束下的偏置比例導引律
2.1落角約束下比例導引的局限性
比例導引制導律可表示為
(10)
式(10)兩邊積分得
(11)
比例導引打擊地面慢速移動目標時,彈道終端過載接近于零,碰撞前的某一微小時間段內終端彈體速度矢量和終端彈目相對速度矢量基本保持不變,因此彈道終端的彈目相對速度與彈目連線重合,即有
(12)
將式(1)和式(12)代入式(10)中,得
(13)
由于紅外制導彈藥彈體速度遠大于地面目標速度,可知Δθ為小量,有
(14)
彈體的終端落角θf取決于有效導航比N、初始彈目視線角qi和初始相對速度方向角εR,i。有效導航比一般取值為3≤N≤5,因此比例導引制導律的落角范圍
(15)
理論上比例導引可以實現大落角,而真實情況中制導初始時刻的彈目視線角與相對速度方向角限制了比例導引制導律落角的范圍。
2.2彈道成型最優制導律
Zarchan利用Schwartz不等式推導出了彈道成型最優制導律[10],使得控制能量需求最小的同時,實現了落點與落角的雙重約束,并成功應用于Apollo飛船登月等一系列重大工程項目,彈道成型制導律形式為
(16)
式中,tgo表示剩余飛行時間;qt表示當前彈目視線角;Γ表示期望落角。由于執行過程需要剩余飛行時間信息,從而產生了對額外的硬件需求問題,增加了彈體的復雜性,提高了生產成本。
2.3偏置比例導引制導律
彈道成型可以實現落角控制的根本原因是在其比例導引基礎上復合了與剩余飛行時間和期望落角相關的偏置項。基于上述思想,通過在等式(8)右端加偏置項構成偏置比例導引律[13]:
(17)
式中,b表示偏置項。導引律兩邊積分得
(18)
由于偏置比例導引末端過載接近于零,同樣彈道末端彈目相對速度與彈目連線重合,式(12)代入式(18)可得到期望落角Γ與需用偏置積分量BN之間的函數關系:
(19)
偏置比例導引律通過偏置項積分量B來實現對落角的精確控制。整個彈道飛行過程中,只要保證偏置項積分量B達到需用偏置積分量BN,終端落角為即為期望落角Γ。其中,初始彈目視線角qi可由載機或者地面裝訂;終端相對速度傾角Γ+Δθ與初始相對速度傾角θR,i可分別由式(7)、式(8)計算獲得。
考慮到真實過載方向只能沿彈體速度法向,因此偏置比例導引律的過載指令為
(20)
由于相對速度與彈體速度夾角很小,為便于工程應用,將式(7)代入式(20)中,得到
(21)
3 彈道穩定性分析與偏置項分配
3.1彈道的閉環解
將偏置比例導引律引入到彈目相對運動數學模型中,獲得偏置比例導引律的彈道非線性模型
(22)
對方程組無量綱化,令ρ=|b|R/vR,dτ=|b|dt,可得到
(23)
式中,σ表示偏置項b的符號,方程組平衡點坐標為{ρe,εe}={σ(N-1),π/2}。式(23)中的兩個子式相除,得到
(24)
為使得彈體末端過載收斂,有效導航比取N>2。解微分方程得到有效導航比N>2時的無量綱彈道閉環通解:
(25)
式中,c為積分常數,其值取決于無量綱距離初值ρ0和相對速度方向角εR0。積分常數在平衡點處的值為
(26)
3.2彈道的穩定域
彈道的穩定性可通過相平面軌跡圖中無量綱距離的收斂性來判斷。為了滿足工程中增大落角的需求,主要研究偏置項大于零的情況,此時σ=1,同時令導航比N=4,從而得到關于無量綱距離ρ和相對速度方向角εR的相平面軌跡圖,如圖3所示。圖中每條相平面軌跡上的標識數字為其對應的積分常數c,實心圓點表示平衡點,其坐標為(ρe,εe)=(3,π/2),對應積分常數ce=-1/54。圖中的軌跡簇被平衡點分為A、B、C和D共4組,每條箭頭指向表示對應組曲線隨時間變化的收斂方向。其中A、C兩組軌跡無量綱距離收斂到零,表明其彈道穩定收斂到目標;而B、D兩組曲線是發散的。

圖3 相平面軌跡(N=4)Fig.3 State plane trajectories (N=4)
可見,彈道穩定性取決于積分常數c和初值ρ0,穩定域為:{c
在已知初始條件ρ0和ε0的情況下,彈道穩定的判斷策略如圖4所示。當c>ce,ρ0>ρe或c 圖4 初始條件下彈道穩定性判定策略圖Fig.4 Diagram of judgement strategy for trajectory stability under certain initial conditions 3.3偏置比例導引偏置項分配 由于不能事先準確獲得整個彈道飛行時間信息,為保證偏置積分量B達到需用偏置積分量BN,應使得偏置持續時間H小于真實彈道飛行時間。同時,為保證穩定性分析有效,應使得當前偏置項大小與相對速度vR成正比。 (27) 此時,初始偏置量b0取為 (28) 當前偏置項根據初始偏置項來計算得出 (29) 盡管偏置持續時間計算不準確,但考慮真實彈道較彎 曲且導彈速度基本不變,所以仍然可以保證偏置持續時間小于彈道真實飛行時間。 整個彈道由偏置比例導引段和比例導引段組成。偏置比例導引段完成需用偏置積分量后,切換至比例導引,然后由比例導引最終實現落角與落點的精度控制。 根據前面相平面軌跡分析可知,對于比例導引制導段,在切換點處必定存在一定初始相對速度方向誤差角εRM,當此段飛行時間不足以消除相對速度方向誤差的影響時,將會影響到整個彈道的落角精度與制導精度。 4.1偏置比例導引律制導性能研究 為研究期望落角Γ、偏置起始時間t1、偏置持續時間H和有效導航比N對偏置比例導引律制導性能的影響,仿真條件設為6個場景,仿真所得需用偏置積分量、起始偏置、實際終端落角、脫靶量和控制能量需求如表1所示,其中偏置持續時間H的變化通過調整初始偏置項大小來間接實現。仿真所得偏置項、縱向平面彈道、指令過載、目標視角和控制能量需求曲線如圖5~圖9所示。 表1 偏置比例導引性能研究仿真場景設置 圖5 偏置比例導引偏置項曲線Fig.5 Bias profile of biased PNG 圖7 偏置比例導引指令過載曲線Fig.7 Command acceleration histories of biased PNG 對比場景1、場景2和場景3可知,增大期望落角Γ,需用偏置積分量、初始偏置增大;并且飛行過程中的最大需用過載、控制能量需求和目視視角都會增大;當存在過載與目標視角限制時,期望落角并不是越大越好。由于落角增大使得比例導引段飛行時間加長,導致初始相對速度方向誤差εRM的影響減小,使得整個彈道終端落角與制導精度明顯提高。 圖8 偏置比例導引目標視角曲線Fig.8 Look angle variations of biased PNG 圖9 偏置比例導引能量消耗曲線Fig.9 Control effort curve of biased PNG 對比場景2與場景4,偏置起始時間t1后移可有效降低彈道高度并縮短飛行時間,但增大了最大需用過載與控制能量需求。由于起始比例導引段飛行時間縮短,并且導引頭進入盲區時保持過載與實際過載需求偏差增大,導致落角精度與制導精度有所降低。 對比場景2與場景5,適度減小偏置持續時間H,可明顯提高落角與制導精度并有效降低最大需用過載。原因在于H的減小增大了比例導引段飛行時間,同時使得切換時刻彈目距離增大,從而減小了切換時刻彈目視線角速度。而當偏置持續時間H過小時,意味著偏置項過大,將使偏置比例導引段彈道失穩,目標視角的急劇增大,使得目標易出視場,如圖8所示。 對比場景2與場景6,有效導航比N增大,需用偏置積分量BN增大,從而使得偏置項增大,最大需用過載與控制能量需求提高;同時更長比例導引飛行時間與盲區更小的過載保持大大提高了落角與制導精度。 綜合對比分析,適度減小偏置持續時間可以作為提高落角與制導精度的同時又能降低最大過載的一種有效手段。 4.2與彈道成型最優制導律的對比研究 為對比偏置比例導引與彈道成型最優制導律的性能,共設定6個仿真場景,具體參數設置及相應的落角精度、制導精度與最大需用過載如表2所示。兩種制導律的縱向彈道、過載、目標視角和控制能量需求曲線分別如圖10~圖13所示。 兩種制導律均能在命中運動目標的情況下準確實現落角約束;偏置比例導引落角和制導精度低于彈道成型。減小偏置持續時間可以增大比例導引段飛行時間,有效提高偏置比例導引的落角與制導精度,使其接近于彈道成型落角與制導精度,如表2所示。 表2 兩種制導律對比研究仿真場景設置 偏置比例導引的彈道高度大于彈道成型,彈道更加彎曲,使得其飛行時間大于彈道成型飛行時間,如圖10所示。 圖10 兩種制導律的縱向彈道對比Fig.10 Spatial trajectories comparison between biased PNG and trajectory shaping guidance 對于彈道末段過載的需求,偏置比例導引逐漸減小,而彈道成型則單調增大;前者最大需用過載出現在彈道中段,后者則出現在彈道末端;盡管偏置比例導引最大需用過載大于彈道成型,鑒于實際情況末制導段速度逐漸減小,偏置比例導引并不比彈道成型更容易出現過載飽和現象。同樣可通過減小偏置持續時間使其大落角下的最大需用過載接近于彈道成型最大需用過載,如圖11所示。 圖11 兩種制導律的縱向過載對比Fig.11 Command acceleration comparison between biased PNG and trajectory shaping guidance 采用偏置比例導引制導過程中,其目標視角大于彈道成型的目標視角,且二者差距隨著期望落角或偏置項的增大而增大,如圖12所示。 圖12 兩種制導律的目標視角對比Fig.12 Look angle comparison between biased PNG and trajectory shaping guidance 偏置比例導引的控制能量需求大于彈道成型,這是由于彈道成型是基于控制能量最優推導出的最優制導律;且偏置項越小,二者越接近,如圖13所示。 綜合分析可得,偏置比例導引律的落角與制導精度低于彈道成型,最大需用過載大于彈道成型最大需用過載。保證目標視角滿足導引頭視場域約束并且滿足彈道穩定性的前提下,盡量減小偏置持續時間可以使其落角與制導精度接近彈道成型的同時,保證大落角約束下的最大過載接近于彈道成型最大過載。 圖13 兩種制導律的能量消耗對比Fig.13 Control effort comparison between biased PNG and trajectory shaping guidance 本文采用的偏置比例導引律本質上是偏置比例導引加比例導引的組合制導律,偏置比例導引可視作為比例導引的中制導,負責將導彈導引至滿足比例導引實現期望落角所需的特定初始條件,然后由比例導引最終實現落點與落角的約束,其中比例導引段飛行時間影響著落角與制導精度。 研究表明:適度減小偏置持續時間可以提高落角與制導精度的同時又能降低最大過載;通過合理設計偏置持續時間,可使得偏置比例導引律在落角精度、制導精度與最大需用過載這些關鍵的制導性能方面接近于彈道成型制導律。同時,其相對于彈道成型制導律的最大優勢在于偏置比例導引律無需剩余飛行時間信息,更適用于打擊地面運動裝甲目標的紅外成像制導彈藥。 [1]XuLJ,ChenHX.Improvementofinfraredhorizondetectorusingtwo-dimensionalinfraredtemperaturedistributionmodel[C]∥Proc.of the AIAA Guidance, Navigation, and Control Conference, 2015: 335-347. [2]MainiAK,VermaAL,AgrawalV.Targetsimulatorforserviceabilitycheckofinfrared-guidedmissiles[J].Journal of Spacecraft and Rockets, 2011, 48(1): 175-181. [3]SonawaneHR,MahulikarSP.Effectofmissileturnrateonaircraftsusceptibilitytoinfrared-guidedmissile[J].Journal of Aircraft, 2013, 50(2): 663-667. [4]RatnooA,GhoseD.Impactangleconstrainedguidanceagainstnonstationarynonmaneuveringtargets[J].Journal of Guidance, Control, and Dynamics, 2010, 33(1):269-275. [5]LinDF,QiZK,XiaQL.Designandidentificationonparametersofproportationnavigationguidancelawwithgravityovercompensation[J].Journal of System Simulation, 2006, 18(10):2753-2756.(林德福,祁載康,夏群力. 帶過重力補償的比例導引制導律參數辨識與設計[J].系統仿真學報,2006,18(10):2753-2756.) [6]KimM,GriderKV.Terminalguidanceforimpactattitudeangleconstrainedflighttrajectories[J].IEEE Trans. on Aerospace and Electronic Systems, 1973, 9(6): 852-859. [7]ChoHQ,RyooCK,TsourdosA,etal.Optimalimpactanglecontrolguidancelawbasedonlinearizationaboutcollisiontriangle[J].Journal of Guidance, Control, and Dynamics, 2014, 37(3): 958-964. [8]LeeCH,KimTH,TahkMJ,etal.Polynomialguidancelawsconsideringterminalimpactangleandaccelerationconstraints[J].IEEE Trans.on Aerospace and Electronic Systems, 2013, 49(1): 74-92. [9]ParkBG,KimTH,TahkMJ.Optimalimpactanglecontrolguidancelawconsideringtheseeker’sfield-of-viewlimits[J].Journal of Aerospace Engineering, 2013, 227(8): 1347-1364. [10]PaulZ. Tactical and strategic missile guidance[M]. 6thed.Lexington:ProgressinAstronauticsandAeronautics, 2012: 569-601. [11]RatnooA,HayounS,GranotA,etal.Pathfollowingusingtrajectoryshapingguidance[C]∥Proc.of the AIAA Guidance, Navigation, and Control Conference, 2013: 5233-5255. [12]WangH,LinDF,WangJ,etal.Analysisandapplicationstudyontheextendedtrajectoryshapingguidancelaw[J].Acta Armamentarii, 2013, 34(7): 801-809. (王輝,林德福,王江,等. 擴展彈道成型末制導律特性分析與應用研究[J].兵工學報, 2013, 34(7): 801-809.) [13]WangH,LinDF,CuiXX.Extendedtrajectoryshapingguidancelaws[J].Transactions of Beijing Institute of Technology, 2014, 34(6): 597-602. (王輝,林德福,崔曉曦. 一類擴展彈道成型制導律[J].北京理工大學學報, 2014, 34(6): 597-602.) [14]WangH,WangJ,LinDF,etal.Analyticstudyonextendedtrajectoryshapingguidancesystemwithfirst-orderautopilotdynamics[J].Systems Engineering and Electronics, 2014, 36(3): 509-518.(王輝,王江,林德福,等.考慮一階駕駛儀動力學的擴展彈道成型制導系統解析研究[J].系統工程與電子技術,2014,36(3): 509-518.) [15]KimBS,LeeJG,HanHS.BiasedPNGlawforimpactwithangularconstraint[J].IEEE Trans. on Aerospace and Electronic Systems, 1998, 34(1): 277-288. [16]LeeCH,KimTH,TahkMJ.BiasedPNGfortargetobservabilityenhancementagainstnonmaneuveringtargets[J].IEEE Trans. on Aerospace and Electronic Systems, 2015, 51(1): 55-72. [17]KoraySE.IndirectcontrolofimpactangleagainststationarytargetsusingbiasedPPN[C]∥Proc.of the AIAA Guidance, Navigation, and Control Conference, 2010: 8148-8154. [18]KoraySE,OsmanM.Indirectimpactanglecontrolagainststationarytargetsusingbiasedpreproportionalnavigation[J].Journal of Guidance, Control and Dynamics, 2012, 35(2): 700-703. [19]KoraySE.Controlofimpactangleusingbiasedproportionalnavigation[C]∥Proc.of the AIAA Guidance, Navigation, and Control Conference, 2013: 5113-5127. [20]TekinR,KoraySE.Switched-gainguidanceforimpactanglecontrolunderphysicalconstraints[J].Journal of Guidance, Control, and Dynamics, 2015,38(2):205-216. Biased proportional navigation applicable for infrared guidance munitions WANG Guang-shuai1, LIN De-fu1, FAN Shi-peng2, ZANG Lu-yao1 (1. School of Aerospace Engineering, Beijing Institute of Technology, Beijing 100081, China;2.BeijingAerospaceAutomaticControlInstitute,Beijing100854,China) Considering trajectory shaping guidance is unavailable for the constraint of the impact angle of infrared guidance munitions which could not supply time-to-go information, a kind of biased proportional navigation guidance, without time-to-go for its input, is proposed. Based on the established munitions-target relative motion model and collision triangle, the relationship between the desired impact angle and the demand bias integral quantity is derived. Then, the differential equation of engagement kinematics is solved and the stable region is obtained. The influence of some relevant factor on guidance performance of the proposed guidance is studied. The biased proportional guidance performance is also compared with that of the trajectory shaping guidance. Simulation results show that the biased proportional navigation is competitive with the trajectory shaping guidance in the key performance indexes, such as impact angle control precision, guidance and control precision and the maximum demand acceleration and that it could be used for the constraint of impact angle of infrared guided munitions. trajectory shaping guidance; infrared guidance munitions; biased proportional navigation; constraint of impact angle 2015-07-30; 2015-12-15;網絡優先出版日期:2016-06-02。 國家自然科學基金(61172182)資助課題 TJ 765.2 A 10.3969/j.issn.1001-506X.2016.10.18 王廣帥(1987-),男,博士研究生,主要研究方向為飛行器制導與控制。 E-mail:wangguangshuai88@sina.com林德福(1971-),男,教授,博士,主要研究方向為飛行器制導與控制。 E-mail:lindf@bit.edu.cn范世鵬(1986-),男,博士,主要研究方向為飛行器制導與控制。 E-mail:fspzxm@sina.com臧路堯(1987-),男,博士研究生,主要研究方向為飛行器制導與控制。 E-mail:luyao_jizi@126.com 網絡優先出版地址:http://www.cnki.net/kcms/detail/11.2422.TN.20160602.1526.004.html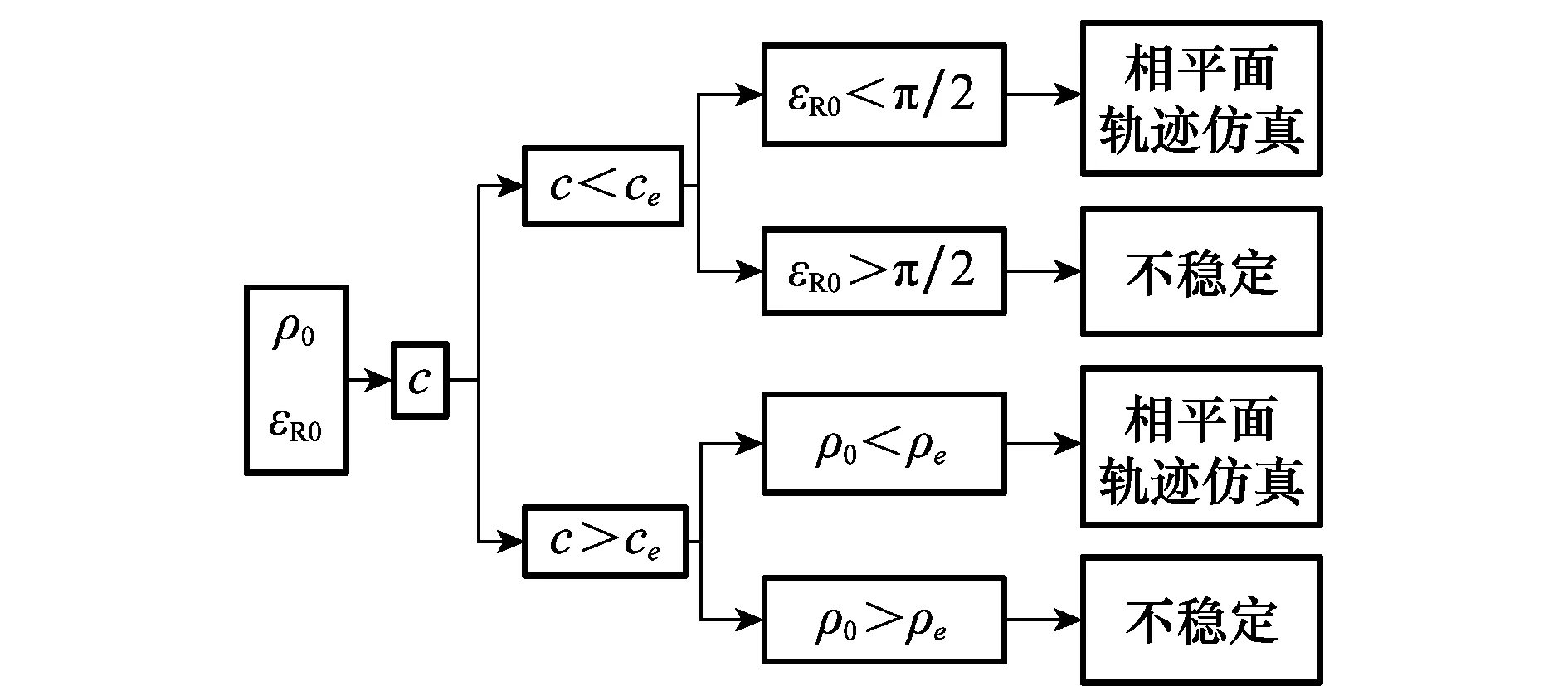
4 仿真分析

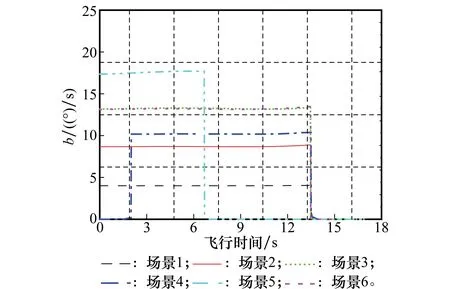





5 結 論

