基于組合模型的網絡流量預測
王雪松,李蘇洋
基于組合模型的網絡流量預測
王雪松,李蘇洋
網絡流量是多種因素綜合作用的結果,具有一定的混沌性和非線性,為了對網絡流量將來變化趨勢進行準確預測,提出了一種網絡流量的組合預測模型(PHR-ELM)。分別采用C-C算法和Cao算法對原始網絡流量數據進行混沌分析,構建極限學習機的訓練樣本集和測試樣本集,然后將訓練樣本輸入到極限學習機進行學習,建立網絡流量預測模型,最后測試樣本集輸入到模型中進行單步和多步預測的驗證性實驗。結果表明,PHR-ELM可以反映網絡流量的混沌性和非線性變化趨勢,獲得了高精度的網絡流量預測結果,且預測結果要優于其它模型。
網絡流量;組合建模;混沌特性;極限學習機;相空間重構
0 引言
隨著網絡用戶數量的不斷增加,以及各種網絡業務增加,網絡阻塞的頻率日益增加,如何保證網絡正常工作面臨巨大的挑戰[1,2]。網絡流量預測是解決該問題的一種途徑,其預測結果可幫助人們提前知道網絡的變化信息,因此如何提高網絡流量的預測精度直接影響網絡管理水平的高低[3]。
為了更好的保證網絡正常運行,防止網絡擁塞現象的出現,人們通過各種途徑、采用多種技術對網絡流量預測進行了探索和研究,當前使用最為廣泛的方法為時間序列分析法[3],它們按時間收集網絡流量變化的歷史數據,然后采用線性回歸方法對數據進行分析,找出其中隱藏的變化規律,對于小規模的網絡,它們具有建模速度快、效率高,預測結果可靠等特點[4,5],然而現代網絡的規模大,使得網絡流量具有強烈的非線性,時間序列分析法僅能描述線性變化趨勢,無法實現網絡流量的非線性建模與預測,局限性明顯[6]。為了解決傳統時間序列方法存在的問題,學者們引入了一些非線性預測算法對網絡流量數據進行建模與分析,如BP神經網絡、RBF神經網絡、支持向量機、最小二支持向量機等,取得了更好的網絡流量預測效果[7-10]。對大規模網絡流量數據,支持向量機以及最小二支持向量機的訓練時間長,無法實現網絡流量的在線預測[11];BP神經網絡、RBF神經網絡要經過多次迭代才能確定網絡結構,收斂速度慢,且參數難以確定[12]。隨著網絡流量預測研究的不斷深入,人們發現網絡流量具有一定的混沌特性,因此在網絡流量預測建模,如何將混沌理論與非線性理論結合起來以提高網絡流量預測的準確性,是當前主要研究的方向[13,14]。
極限學習機(extreme learning machine,ELM)是一種根據Moore-Penrose廣義逆矩陣理論的神經網絡,通過線性方程組對訓練迭代進行求解,一次可以完成訓練,不存在傳統神經網絡的問題,且具有支持向量機的預測性能[15]。本文將混沌理論和ELM組合在一起,提出一種網絡流量預測的給合模型(PHR-ELM),首先采用C-C算法和Cao算法構建網絡流量的訓練樣本集和測試樣本集,然后采用極限學習機對訓練樣本集和測試樣本集進行學習和性能測試,驗證PHR-ELM的網絡流量預測的有效性和優越性。
1 PHR-ELM的網絡流量預測模型
1.1混沌理論
網絡流量受到網絡價格、用戶上網時間以及上網人心理因素的影響,且因素之間互相影響,導致網絡流量變化一定的混沌特性,要進行網絡流量準確建模,首先就要分析其混沌性,重建模學習樣本。設網絡流量數據為{x(tj), j=1,2,…,n},那么網絡流能夠重構為公式(1):

式中,τ為延遲時間,m為嵌入維數。
1.1.1C-C算法
(1)本文選擇C-C算法對網絡流量的τ進行分析,得到網絡流量數據之間的時間相關性,設X(i)=[x(i), x(i+τ),L ,x(i+(m-1)τ)]和X(j)=[x(j), x(j+τ),L ,x(j+(m-1)τ)]分別表示相空間的相鄰點,則兩點間的距離為公式(2):

采用關聯積分描述點對數所占比例,具體為公式(3):
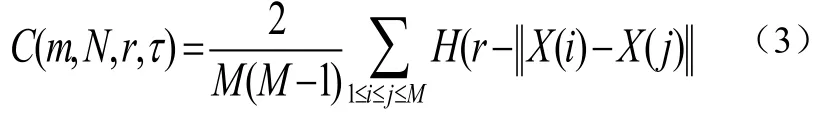
公式(3)中,r為臨界半徑為;N為序列規模;H(·)表示Heaviside函數,具體為公式(4):

全部網絡流量被劃為t個子序列,得到它們的統計量為公式(5):

設ΔS(m,t)=max[S(m, rj,τ)]-min[S(m, rj,τ)],則有公式(6):

公式(6)中,l和k分別表示可能的最大和最小嵌入維數。
1.1.2CAO算法
采用Cao算法對網絡流量數據的嵌入維數m進行分析,設Xi(m+1)和Xn(i,m)(m+1)分別表示第i個重構向量Xi(m+1)和其最近鄰,則有公式(7):

1.2極限學習機(ELM)

公式(8)中,k為訓練集規模;αi為輸入權值,bi為偏差;βi為輸出權值。
對公式(8)進行矩陣變換,可以得到公式(9):

公式(9)中,Tk為輸出向量;Hk為神經元矩陣,其定義如公式(10):

一般條件下,K>>L,通過式(10)可以得到輸出權值為公式(11):

根據
iβ就可以確定ELM,然后采用ELM對網絡流量訓練樣本進行重新學習,建立如下的網絡流量預測模型為公式(12):

1.2網絡流量的預測過程
(1)對一個具體網絡服務器,采用數據采集軟件收集原始網絡流量。
(2)網絡流量具有一定的波動性,為了消除數據值波動過大帶來的負面作用,其對原始數據進行預處理,具體為
公式(13):

公式(13)中,Ex和σx分別為網絡流量的均值和標準差。
(3)分別采用C-C算法和Cao算法對原始網絡流量數據進行混沌分析,構建極限學習機的訓練樣本集和測試樣本集。
(4)訓練樣本輸入到極限學習機進行學習,建立網絡流量預測模型。
(5)測試樣本集輸入到模型中進行單步和多步預測的驗證性實驗。
2 網絡流量的預測結果測試
2.1網絡流量數據
為了分析PHR-ELM的網絡流量預測效果,選擇一個主節點路由器的每小時網絡流量作為研究對象,具體如圖1所示:

圖1 仿真對象
選擇最后100個數據對PHR-ELM的泛化能力進行分析,其它樣本作為訓練樣本集建立基于PHR-ELM的預測模型。
2.2重建網絡流量樣本
分別采用C-C算法和Cao算法對圖1中的網絡流量進行分析,它們仿真結果變化曲線如圖2所示:


圖2 網絡流量的τ和m確定
2.3單步預測性能分析
將訓練樣本集輸入到ELM進行學習,并建立單步預測模型,測試樣本的預測結果如圖3所示:
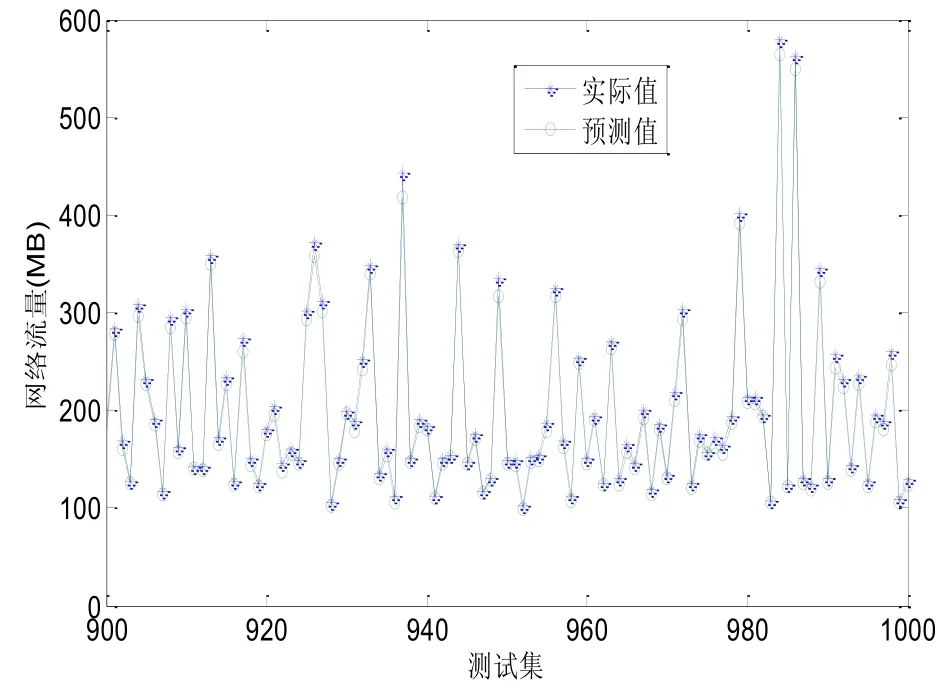
圖3 PHR-ELM的預測結果
從圖3可以看出,PHR-ELM可以很好的跟蹤網絡流量變化態勢,預測值與網絡流量值之間的偏差很小,可以忽略不計,從而獲得較高的網絡流量預測精度高,初步驗證了PHR-ELM應用于網絡流量預測中的有效性。
2.4多步預測性能分析
網絡流量建模的目的是對網絡將來狀態進行描述,而單步預測只是一種短期預測方式,無法對將來的網絡流量進行刻畫,為此要進行網絡流量的多步預測性能分析,本文進行提前2步和4步預測實驗,結果如圖4(a)、(b)所示:

圖4 PHR-ELM的多步預測結果
對圖4(a)、(b)的預測結果進行分析發現,隨著預測步長的增加,PHR-ELM的網絡流量預測誤差越來越大,但預測誤差仍然還是控制在實際要求的范圍內。
2.5與當前其它模型的性能比較
為了分析PHR-ELM的結果更具說服力,選擇當前預測性能較好的網絡流量預測模型進行對照測試,具體為:極限學習機+沒有混沌分析(ELM)、PHR-BPNN、文獻[14]和文獻[15]模型,采用平均百分相對誤差(MAPE)進行衡量,其定義如公式(14):

公式(14)中,n為測試樣本的數量。
PHR-ELM與對照模型預測結果的MAPE如表1所示:

表1 與其它網絡流量預測模型的誤差比較
對表1模型的MAPE進行對比分析可以發現,與其它模型相比,PHR-ELM有效降低了網絡流量的預測誤差,獲得了更高的預測精度,驗證了PHR-ELM的優勢。
3 總結
網絡流量預測可以幫助網絡管理人員提前了解網絡流量的態勢,有利于防止網絡阻塞,一直是學者們關注的焦點,本文提出一種基于PHR-ELM的網絡流量組合預測模型,首先挖掘原始網絡流量數據的混沌特征,對數據進行重建,然后采用極限學習機挖掘網絡流量的非線性變化特征,建立網絡流量預測模型。驗證性實驗結果表明:PHR-ELM可以獲得高精度的網絡流量預測結果,且相對于其它預測模型,具有比較明顯的優勢,可以為網絡管理員提供價值的信息。
[1] Nguyen T T, Armitage G. A survey of techniques for internet traffic classification using machine learning [J]. IEEE Communications Surveys and Tutorials, 2008,10(4): 56- 76.
[2] 姜明,吳春明,張曼,胡大民. 網絡流量預測中的時間序列模型比較研究[J]. 電子學報, 2009, 37(11):2353-2358
[3] Callado A, Keu R J, Sadok D, et a1. Better network traffic identification through the independent combination of techniques [J]. Journal of Network and Computer Applications, 2010, 33(4):433-446.
[4] 董夢麗,楊庚,曹曉梅. 網絡流量預測方法[J]. 計算機工程. 2011, 37(16):98-100
[5] 高波,張欽宇,梁永生,等. 基于EMD及ARMA的自相似網絡流量預測[J]. 通信學報, 2011, 32(4): 47-56.
[6] Jin Yi, Zhou Gan. Theoretical mean-variance relationship of IP network traffic based on ON/OFF model [J]. Article Science in China Series F: Information Sciences, 2009,52(4): 645-655.
[7] 賴錦輝,梁松. 一種新的基于GCS-SVM的網絡流量預測模型[J]. 計算機工程與應用, 2013, 49(21): 75-78.
[8] 趙振江. 基于PSO-BP神經網絡的網絡流量預測與研究[J]. 計算機應用與軟件, 2009, 26(1): 218-221.
[9] 姚奇富,李翠鳳,馬華林,張森. 灰色系統理論和馬爾柯夫鏈相結合的網絡流量預測方法[J]. 浙江大學學報(理學版), 2012, 34(4):396-400.
[10] 李明迅,孟相如,袁榮坤. 融合提升小波降噪和 LSSVM的網絡流量在線預測[J]. 計算機應用, 2012,32(2):340-342,346.
[11] 魏永濤,汪晉寬,王翠榮,張琨. 基于小波變換與組合模型的網絡流量預測算法[J]. 東北大學學報(自然科學版), 2011, 32(10):1382-139.
[12] 王雪松、梁昔明. 基于BPSO-RBF神經網絡的網絡流量預測[J]. 計算機應用與軟件, 2014, 31(9):102-105
[13] 王雪松,趙躍龍. 遺傳算法優化延遲時間和嵌入維的網絡流量預測[J], 計算機工程與應用, 2014, 50(12):66-70
[14] 羅贅騫,夏靖波,王煥彬. 混沌-支持向量機回歸在流量預測中的應用研究[J]. 計算機科學, 2009, 36(7):244-246.
[15] 黨小超,郝占軍. 季節周期性Elman網絡的網絡流量分析與應用[J]. 計算機工程與應用, 2010, 46(28): 98-101.錦軍, 王執銓. 一種基于混沌特性的網絡流量改進預測算法. 兵工學報, 2007, 28(11): 1346-1350.
Network Traffic Prediction by Using Combination Model
Wang Xuesong1, Li Suyang2
(1.Department of Electronic Information, FoShan Polytechnic College, FoShan 528137, China;2. Faculty of Electromechanics Engineering, Guangdong University of Technology, Guangzhou 510006, China)
Network traffic is the result of many factors, which is chaos and nonlinear. A combined prediction model of network traffic is proposed to predict the future trend of network traffic accurately by using combination model. C-C algorithm and Cao algorithm are separately used for chaotic analysis of original network traffic data to construct training set and test set, and then training samples are input into extreme learning machine to learn and establish prediction model, finally, test samples are input into the model to verify the performance by using single step and multi-step prediction experiments. The results show that PHR-ELM can reflect the network traffic chaos and nonlinear trend, predict the results of network traffic with high accuracy, and the prediction results are better than other models.
Network Traffic; Establish Model; Chaotic Characteristics Extreme Learning Machine; Phase Space Reconstruction
TP391
A
1007-757X(2016)06-0011-04
2015.12.02)
廣東工業大學校博士啟動基金資助項目(405105015);佛山職業技術學院科研專項(KY2013G04).
王雪松(1974-),男,佛山職業技術學院,電子信息系,副教授,碩士,研究方向:神經網絡、粒子群算法、物聯網應用,佛山,528137
李蘇洋(1974-),女,廣東工業大學,電機工程學院,講師,博士,研究方向:RFID研發、數值優化設計,廣州,510006

