基于PSS/E自定義模型的風力發電系統動態特性研究

王紅亮（國網湖南省電力公司邵陽供電分公司，湖南邵陽422000）

基于PSS/E自定義模型的風力發電系統動態特性研究

王紅亮（國網湖南省電力公司邵陽供電分公司，湖南邵陽422000）

自然界中風速變化的隨機性、波動性和間歇性，使得風力發電輸出的功率具有不確定性，嚴重影響電力系統的安全穩定運行。為了研究風力發電對電力系統的影響，建立風力發電機組及風速的相關數學模型并進行仿真是研究該問題的重要手段。本文利用電力系統仿真軟件Power System Simulator for Engineering（PSS/E）的自定義功能建立風電場相關元件的自定義模型（如風速、空氣動力模型等），并將自定義模型用于基于雙饋異步發電機（Double Fed Induction Generator，DFIG）的風力發電系統，研究風速變化時的電網動態特性及網側發生故障時風力發電機的動態特性。本文的開展對于掌握DFIG對電力系統動態特性的影響及基于DFIG風力發電機組的通用數學模型研究具有一定的理論價值和實際意義。

風力發電；PSS/E；風速；DFIG

1　風力發電系統的數學模型

風力發電機的主要組成部分是風輪和發電機，工作原理是當風速足夠大時將吹動風輪，風輪帶動發電機產生交流電，然后交流電通過整流器轉變為直流電給蓄電池充電，蓄電池可以直接供直流負載使用，如果是交流負載，則需要再加一個逆變器把直流電變成交流電使用。

1.1雙饋異步風力發電機數學模型

本文研究的是基于雙饋異步風力發電機的風電系統。雙饋異步風力發電機的組成有兩部分：①繞線轉子異步發電機；②交流勵磁變頻器。

1.2機械傳動系統的數學模型

經典的風力發電機傳動軸系模型可等效為2個或3個質量塊，機械傳動軸的2質塊模型有利于系統的解耦控制，因此本文采用2質塊的機械傳動模型其模型如圖1所示。

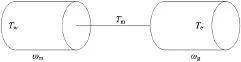
圖1　質塊模型圖

傳動軸的2質塊模型包含2個部分，其中第1個質塊表示旋轉的葉輪的轉動慣量，第2個質塊表示發電機的旋轉慣量。與第1個質塊相關的運動方程是：

式中，Ht表示葉輪與轉軸的轉動慣量，Tw表示氣動轉矩，Tm表示轉軸轉矩，ωm表示轉軸轉速。與第2個質塊相關的運動方程是：

式中，Hg表示轉軸與發電機之間的轉動慣量，ωg表示發電機轉速，Tm表示轉軸轉矩，Te表示電磁轉矩，D表示阻尼系數。

1.3空氣動力部分的數學模型

1.3.1標準的空氣動力學模型

空氣動力學模型的作用是計算風機輸出的機械功率。空氣動力學的標準模型為Pmech=ρπR2VwCp（λ，β）/2。

1.3.2線性空氣動力學模型

線性空氣動力學模型的使用范圍較小，只適用于網側發生擾動后風速保持一定時間不變的情況。

1.4風速模型

風力發電機組的風能來源屬于自然風，而風速具有隨機性，波動性和間歇性，很難保證恒定風速，只要有風速的存在風電系統就承受著或大或小的擾動，這種擾動直接對電力系統的運行帶來影響。風能作為風力發電機的原動力，對風速建立適當的模型用于研究各種情況下系統的性能是十分有必要的。一般可將風速模型分為四類，它們分別是基本風、陣風、斜坡風和隨機風。

（1）基本風即額定風速，反映了平均風速，并決定了風力機輸出功率的大小，在進行動態仿真時，可由初始化計算出基本風速V0。

（2）陣風是指突然變化的風速，這種風速對于電力系統來說是一個較大的擾動，因此對于電力系統暫態穩定性的研究也很有意義。

（3）斜坡風是對具有漸變特性的風速的描述。

（4）隨機風是指風速的變化不符合任何變化規律，它描述了風速的隨機性。

1.5槳距角控制部分的數學模型

槳距角的作用：風速過大時，槳距角發揮作用以保持發電機輸出額定功率。當發電機轉速過小，槳距角將不起作用，當發電機轉速過大時，系統通過槳距角的控制作用來抑制其轉速的持續增加，從而保持系統輸出功率為額定功率。本文介紹PI控制的槳距角模型。

2　頻率控制模型

風機中還有一些其它的模塊如頻率控制模塊，當電力系統收到干擾時，會導致系統頻率短暫衰減，而頻率下降的速度及回復常態的時間都受到電網動態特性的影響。在風電系統中，電機將存儲的慣性能量輸送給電網來降低頻率下降的速率，且允許調速器動作，以穩定電網頻率（見圖2）。

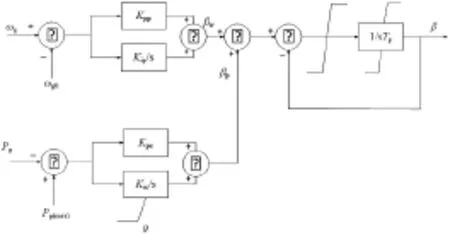
圖2　槳距角控制模型

3　含有風電場接入的電網機電動態特性

3.1引言

隨著越來越多的風電接入電網，人們對含有風電場的電網動態特性的研究也越來越重視，本章通過將風速等相關自定義模型用于基于雙饋異步風力發電機的系統中，以4機2區為基礎，建立含有風機的電力系統，研究風電場接入后對電網的影響以及電網擾動對風力發電系統的影響。

3.2風電接入對電網的影響

本小節分為兩部分來研究風電接入對電網的影響：①陣風對電網的影響；②斜坡風對電網的影響。在經典4機2區系統中添加風電場，在該系統中進行算例仿真。

（1）陣風對電網穩定性的影響

在對比中直觀的看到，風機出力為10MW時，風機在加入槳距角和不加槳距角時風機的出力變化基本沒什么區別，而隨著風機出力的增加，尤其是當風機出力達到100MW時，在沒有槳距角控制的作用下，風機在經歷風速變化后，風機有功功率回不到原來的狀態，影響到系統的穩定運行。所以風機出力越大槳距角控制作用越明顯。

（2）斜坡風對電網穩定性的影響

PSS/E仿真過程：斜坡風起始時間為1s，持續5s，其最大風速時比初始風速大5m/s。通過對通道的選擇觀察了風機系統的有功功率，無功功率，槳距角，G1、G2、G3、G4的有功功率變化。

通過對圖像的觀察可以得出如下結論：

（1）風速增大時風機轉速增大，在槳距角控制系統的作用下，通過增大槳距角來抑制輸出功率的增加，保持發電機輸出為額定功率。

（2）系統經過風速的變化后，G1、G2、G3、G4的有功功率基本都能恢復原來的狀態。

3.2.1電網擾動對風力發電系統的影響

本小節同樣分為兩部分來研究風電接入時，電網擾動對風力發電系統的影響。①有風速變化時電網擾動對風力發電系統的影響；②只有初始風速電網擾動對風力發電系的影響。

（1）有風速變化（斜坡風）時電網擾動對風力發電系統的影響。

（2）只有初始風速時電網擾動對風力發電系統的影響。

3.2.2在原系統中加入不同容量風機研究其對電網的影響

本小節在原4機2區系統中接入不同容量的風機，觀察在有陣風風速變化時對電網穩定的影響。

（1）12號風機出力為15W時，通過PSS/E仿真觀察任意普通發電機的有功變化（如G1）。

圖3　G1有功變化

（2）12號風機出力為50W時，通過PSS/E仿真觀察任意普通發電機的有功變化（如G1）。

（3）12號風機出力為100W時，通過PSS/E仿真觀察任意普通發電機的有功變化（如G1）。仿真結果如圖4所示。

結論：

通過對比三者仿真圖形，可知在原系統其它發電機保持輸出功率不變的情況下，加入不同容量的風機后，在經過風速變化后，系統恢復到穩定運行所需的時間基本一致，不同的是發電機有功變化的最大幅度，且由3.2.1仿真可知，風機出力過小時，之所以G1有功變化不呈現波動性，原因是風機在系統的調節作用不明顯，再來對比風機出力為50MW和100MW，對比兩者仿真圖可知，在系統運行中，風機出力的不同會影響到發電機有功變化的最大幅度。風機出力為100MW的系統中，當風電場經歷風速的變化后，經過控制調節后在此過程中可觀察到發電機有功功率的變化波動性較強，同樣也可以初步推測風機出力越大，風機控制系統的控制作用越明顯。

圖4　G1有功變化

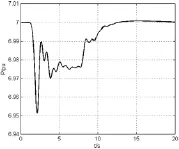
圖5　G1有功變化

3.3多臺風機接入對電網穩定性的影響

在實際的發電系統中，風機接入電力系統的臺數往往是較多的，因此研究多臺風機接入電網對電網穩定性的影響很有必要。本小節仍是在經典4機2區系統中添加風電場，在該系統中進行算例仿真。

從仿真圖可知，過多的風機接入，在有風速變化時，系統重新恢復穩定狀態需要很長的時間。

3.4機電擾動在鏈式系統中的傳播

擾動無時無刻不在干擾著電力系統的正常運行，電網發生擾動會使得發電機的電磁功率和機械功率失去平衡，發電機則需要通過調節轉速來使得電磁功率和機械功率保持平衡，從而使系統穩定運行。發電機轉子角的變化影響母線電壓相角的變化，從而造成相鄰發電機的功率不平衡，進一步影響發電機轉速的動態特性，擾動便在電網中進行傳播，使得電網中所有的發電機進入另一個狀態。本章節可以讓人們方便的認識機電擾動在電力系統中傳播特性，揭示電力系統的機電動態機理、分析風電機組接入電網時機電擾動的傳播特性很有意義。

3.4.1機電擾動在不含風電場系統中的傳播

本小節采用含有10臺普通發電機的鏈式系統，通過觀測10條母線的頻率變化，來觀察機電擾動對電網是否有影響。

此次仿真：①為了觀察機電擾動在普通鏈式系統中的傳播；②為了給下面含風機的鏈式系統作為對照組（見圖6）。

此處以負荷的變化模擬系統初始擾動，在0s時刻先將母線1上的負荷增加50MW持續0.01s，在減小母線1到原有負荷水平及減少到0MW并讓系統運行1s。通過觀察母線電壓頻率來判斷機電擾動對電網的影響。

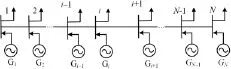
圖6　機鏈式系統

3.4.2機電擾動在含風電場系統中的傳播

通過對比各個曲線第一次達到峰值時所需的時間，發現在無風機鏈式系統和有風鏈式系統中，二者所需的時間基本沒有太大差別 （實際觀察有雙饋異步風力發電機的鏈式系統第一次達到峰值的時間比無風機的鏈式系統第一次達到峰值的時間要快），觀察頻率峰值大小卻發現，5號母線之前，無風機的鏈式系統和有風機的鏈式系統中最大頻率幅值基本沒有太大變化，但5號母線之后，發現無雙饋異步風力發電機的鏈式系統其最大母線頻率幅值較有雙饋異步風力發電機的鏈式系統的最大母線頻率幅值要大不少。

4　結論

本文通過將風速等相關自定義模型用于基于雙饋異步風力發電機的風電系統中，以經典4機2區系統為基礎，建立含有風機的電力系統，研究風電場接入后對電網的影響以及電網擾動對風力發電系統的影響，通過對仿真結果的分析得出結論：風速增大時風機轉速增大，在槳距角控制系統的作用下，通過增大槳距角來抑制輸出功率的增加，保持發電機輸出功率為額定功率。含風機的系統在經歷風速變化后，系統基本都能快速的恢復原來的狀態：當多臺風機接入電網時，系統在經歷風速的變化后，系統重新恢復穩定狀態需要很長的時間；當電力系統發生擾動后，發電機母線頻率呈現一個傳遞的過程，而母線頻率其實對應于發電機轉子角，它會影響到系統中的電壓相角，顯然電壓相角會影響到有功功率的傳輸，總結為：電力系統中的機電擾動會對系統產生不利的影響。

TM315

A

2095-2066（2016）26-0055-03

2016-8-12

王紅亮（1979-），女，工程師，本科，主要從事電力營銷工作。