路基土石方TIN算法的誤差分析及改進探討

胡艷蓮

摘 要：文章計算路基土石方TIN算法理論，對其進行誤差分析并探討其改進方法，在現實工程中提高路基土石方計量的精度。

關鍵詞：TIN算法；誤差分析；改進

目前數字化測繪技術越來越普遍，各種測量數據后處理及應用軟件越來越多，利用TIN算法計算土石方量的以及逐漸取代原先的方法。文章將對針對TIN算法進行誤差分析及改進探討。

1 TIN算法計算路基土石方

斷面法計算路基土石方有個致命的缺點，因為兩相鄰橫斷面間的填挖面積并不是線性或特定規律變化的。從理論上講，土方量的正確計算必須通過三維的地面模型和道路設計模型的疊加運算完成，由此便產生了TIN算法。

根據數模理論，任何復雜的表面（地面、設計面）都可以用三角網表示、模擬，因此，三維土方量計算方法的核心就是每對重合的地面三角形和設計三角形（三角形對）的幾何關系（見圖1.1），其填挖體積的計算不外乎圖示的4種關系。三維土方量的計算方法在理論上是正確的，其土方量以每一塊三角形對應的填挖體積表達。

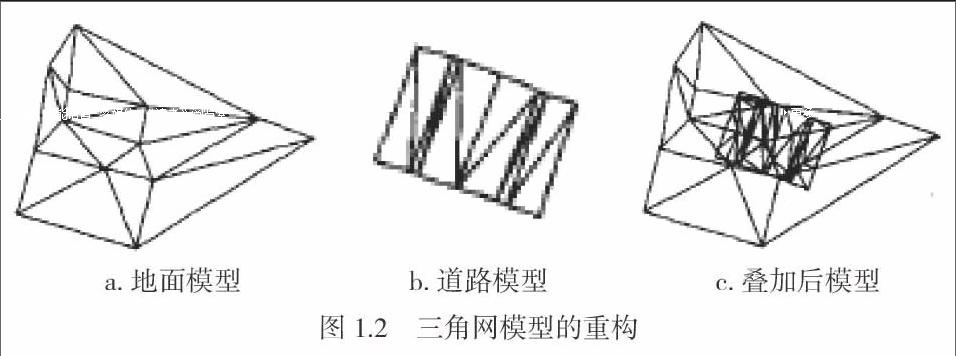
為了能得到滿足道路工程特點的三角形，對道路幾何設計任何階段和成果都可以認為是地面模型和道路設計模型在不同約束條件的重構（見圖1.2）。它演變成道路設計邊界范圍內地面模型和道路模型拼合并形成新的構網點及約束線，然后雙雙重新構網，這樣，便生成了在水平投影完全重合的一一對應的地面三角形和道路三角形，從而得到每個三角形直至整個設計區域的土方填挖體積。三角網模型重構的算法描述如下。

a.地面模型 b.道路模型 c.疊加后模型

圖1.2 三角網模型的重構

（1）對道路模型以橫地面線為約束進行三角化。

（2）在平面上，以道路模型三角網疊加原始地面模型三角網，其相交點設為模型的新增點，道路模型邊界點也設為新增點，所有原先的三角網邊、相交后一邊變成的多邊（含道路模型邊界）均設為約束邊；

（3）對步驟（1）產生的所有點及約束邊進行帶約束的Delaunay三角化（三角網重構）；

（4）在立面上，將道路模型點投影到原始地面模型得到相應高程，同時將原始地面模型點投影到道路模型得到相應高程，并將相交得到的新點分別投影到兩個模型上得到相應的高程；

（5）得到邊網完全重合的道路及原地面模型的三角網，計算每一塊三角形對應的填挖體積；

（6）累加得到相鄰樁號間乃至整個道路范圍內的土方填挖數量。

2 TIN算法誤差分析

根據TIN算法原理可知其誤差主要來源于外業數據采集，即離散高程點的采集。在此過程中會產生如下誤差：測量誤差（由儀器、觀測者和觀測條件引起的誤差）、地形類別引起的誤差以及打點密度的稀疏和位置引起的誤差。

實際上為了使TIN模型能盡量趨近于真實地形，僅有野外采集的高程值是不夠的，還必須有一種高程點間的內插方法，在生成TIN模型之前，需要對原始離散高程點進行內插，并且內插的結果應能完全表達地形。

3 對改進TIN算法的探討

對TIN算法改進的最有效辦法便是先對離散高程點進行適當的空間插值后再生成TIN模型。空間插值的方法有很多，其中適合對離散高程點進行空間插值的方法有反距離權插值、SPILNE樣條函數、克里金插值，TIN法插值。現主要探討利用反距離權插值法對TIN算法進行改進。

反距離權插值是最常用的空間內插方法之一。它假設未知值的點受較近已知點的影響比較遠的已知點更大，影響的程度（或權重）用點之間距離乘方的倒數表示。其通用方程為：

（1）

其中z0是點0的估計值；zi是已知點i的z值；di是已知點到點0之間的距離；s是在插值中用到的已知點的數目；k是指定的冪。冪為1意味著點之間數值變化率恒定，該方法稱為線性插值法，冪為2或更高則意味著越靠近已知點，數值的變化率越大，遠離已知點則趨于平穩，也就是說冪越高，內插結果越具有平滑的效果。

此時我們可以根據反距離權插值思想得到以下TIN算法改進思路：先將測區分為若干個小的圓區域，并確保每個區域內有相同數量的已知高程點；根據反距離插值思想和最小二乘原理擬合出通過該小圓區域內所有已知點的曲面

h=f（x，y） （2）

其中（x，y）為點的平面坐標，h為該點高程。一旦該曲面被擬合出，便可實現該小圓區域內任意位置的空間插值。同理用計算機編程可以實現對該測區內其它小圓區域內未知高程點的空間插值；根據插值后的所有高程點重新構成TIN模型，然后再次回到TIN算法的軌道上進行路基土石方計算。

其實現插值的具體步驟如下：

①確定采用多大面積范圍內的數據點來計算插補點的數值、確定選取多少點參加計算插補點。參加計算插補點的點數初步選為10個，該面積范圍以插補點為圓心的一定半徑的圓，圓的半徑取決于原始高程點的疏密，可由下式求得：

πR2=10（A/N） （3）

其中A為測區面積，N為測量總點數。

②確定權函數。根據反距離權插值思想，圓內各個點位置對插補點的影響是不同的，即距離越遠，影響越小。我們取冪為2，則可得權函數為：

Pi=1/d2 （4）

③擬合通過該小圓區域內已知點的曲面。圓內的10個點可以建立10個誤差方程為：

a1xi2+a2xi2+a3xiyi+a4xi+a5yi+a6-hi=Vi （5）

式中xi、yi、hi（i=1，2，3…，10）為各點的實測位置和高程，根據最小二乘原理，要求所有的誤差平方與其相應的權值乘積之和最小，即有：

（6）

此時通過條件平差便可擬合出通過該小圓區域內已知點的曲面。

④對該小圓區域內任意位置進行高程的空間插值。

此種方法計算開銷少，具有普適性，不需要根據數據的特點對方法加以調整并且當樣本數據的密度足夠大時一般能達到滿意的精度。

4 結語

文章主要是從理論上對幾種路基土石方算法進行了比較和分析然而實際操作中一個道路工程的土石方計算方案需考慮很多因素，包括用于土石方測算的費用，數據源的獲取，道路工程本身對精度的要求等。所以在實際情況中還需要針對具體情況具體分析，反距離差值是提高TIN算法一個不錯的選擇。

參考文獻

[1] 程建川，呂慶禮.道路土方量三維計算方法[J].交通運輸工程學報，2004，4（02）：19-22.

[2] 湯國安，劉學軍等.高程內插方法對DEM所提取坡度、坡向精度的影響[J].地球信息科學學報，2009，11（01）：36-41.