基于“關心”的教學想象和尋繹

沈俊

小學數學遭人詬病的主要原因有二：一是知識的整體性被人為地破壞和拆解，二是教師缺乏對兒童的體認和對其已有經驗的理解。相比而言，后者往往更容易被忽略，導致了數學知識無法結構化，造成了兒童的生活與所面臨現實問題的分離，也使得師生之間原應和諧相長的關系產生了隔閡。

美國學者內爾·諾丁斯提出了“關心倫理”。她強調教育的道德意義，主張教育應該培養有能力、關心人、愛人也值得別人愛的人。[1]這對于教師的課堂教學也有啟示：“朝向兒童”理應成為課堂教學的基礎，“關心兒童”是教師成長的第一專業。

一、從一個案例聯想開去

現在的數學課堂小結已不再拘泥于梳理知識，而更多地趨向于請學生談感受，說收獲，提問題，顯得更加開放多元。學生身處安全融洽的教學場域，情緒容易釋放，思維更加活躍，提出的問題往往也超出了教師的預設。以下是教師執教蘇教版數學四年級下冊第六單元“相遇問題”，學生在課堂小結時提出的問題：

生活中，兩個人面對面走，是不是都會相遇啊？

有沒有兩個人不相遇的情況？

兩個人相遇以后會發生什么事情呢？

兩個人相遇后繼續走下去，會怎么樣呢？

……

對于上述問題，我們該如何處理？是一笑了之，置之不理，還是藝術化留白，去“課外探究”，抑或有針對性地智慧應答？于是，教師的兒童理解、學科知識、教學機智、文化底蘊、美學藝術等專業素養在其中就會起到導向作用，便有機會引發教學的另一種可能。

身處教學現場，我的第一反應就是美感，一種遇見美的訝異和悸動。臺灣作家龍應臺《目送》里有一段話：“我慢慢地、慢慢地了解到，所謂父女母子一場，只不過意味著，你和他的緣分就是今生今世不斷地在目送他的背影漸行漸遠。你站立在小路的這一端，看著他逐漸消失在小路轉彎的地方，而且，他用背影默默告訴你：不必追。” [2]

相遇在一起，又漸次分離——父女母子如是，教與學如是，人生又何嘗不是這樣？也許，這就是“相遇問題”超出了數學學科本身，給我們帶來的哲學啟迪和美感體驗。關注教學內容的哲學與美，對課堂教學意義重大。美學中有“以美啟真”說，即通過美去發現事物的真，教學中亦可以引導兒童通過感受美的光輝去感知數學的學習內容。

二、教學是一種關系的聯結

被視為“當代最偉大的思想家之一”的德國哲學家馬丁·布伯，將自己最精微的思想概括為一本薄薄兩三萬字的小冊子《我與你》，其核心思想就是以“我與你”關系為樞機的“相遇”哲學。他認為，“我與你”的關系涉及到人的整個現時存在，應是一種親密無間、相互對等、彼此信賴、開放自在的關系。人們必須用自己的整個身心對別人的全部存在做出回應，如此，彼此才不會陌生、敵視和傷害。“人呵，佇立在真理的一切莊嚴中且聆聽這樣的昭示：人無‘它不可生存，但僅靠‘它則生存者不復為人。” [3]

用馬丁·布伯的“相遇”哲學來觀照數學教學場域里的師生關系，我們可以揣摩得出，理想課堂中的師生關系應該這樣描述：兒童學習是兒童、數學、教師之間的真實遇見，課堂就是他們相遇的場域，數學教學就是教師帶著數學走向兒童的過程，當三者水乳交融時，學習便能比較好地發生。

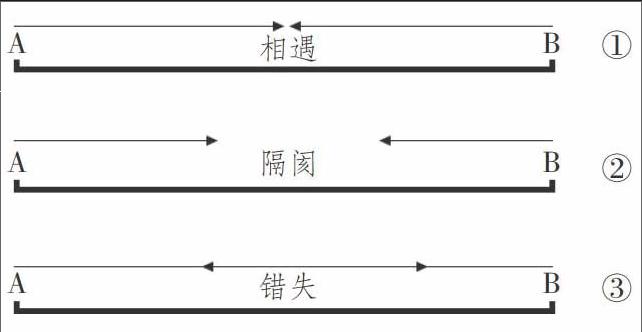
但事實并非如此，教師與兒童的遇見常常如同小學數學里的“相遇問題”（如下圖）：相遇、隔閡與錯失。

1. 相遇

一位老師和一群孩子在同一個班級共同生活了幾年，這何嘗不是一種前世修來的緣分？遇見在一起，就得珍惜，就得用心靠近，用情貼近，用自身的專業修養接近。兒童對師者而言，他的意義就在現時，就在與我們遇見的那一刻、那一節課、那一學期、那幾年。顯而易見，我們不能預見兒童未來會成為誰，是什么樣態，有著何等的成就，我們也無法得知未來。然而，令我們著迷和心醉的是可以把握與兒童相互遇見的現在，他們在我們的關心、扶助和熏陶下，自由活潑地生長。

2. 隔閡

師生雖同處一室，心與心就一定能遇見？更何況一顆心與幾十顆心的關系。所以，只能希望“相遇”是常態，但隔閡不免存在。隔閡有其存在的必然性，如：區域（國家）的教育氣候、大班額難以面面俱到、兒童的身世背景、教師對兒童的認同與理解、教師的教學價值取向、專業素養和文化底蘊等等。這些因素里，有些不可抗拒，但最根本的還是在教師的可控范圍內，隔閡產生的因由多在教師自身。我們改變不了大環境，但可以通過自身的努力，更新理念，改變心態，提升技能，加強修養，影響身邊的人和事，從而影響世界。

從某種意義上看，隔閡所產生的距離也不失為一種美學價值。當兩對凝望遠方的眼神觸碰在一起時，教師和兒童相視一笑，懷著關心和謙遜，踩著共同的節奏，沿著相同的軌跡，向對方走去，他們終會相遇的。

3. 錯失

有相遇和隔閡，就不可避免地存有錯失和擦肩而過，相見未必曾相識，心中難免留下遺憾。然而，在馬丁·布伯的“相遇”哲學里，我們又可以找到慰藉。師生之間的遇見是一種純凈的關系，它既超越時間又稽留于時間，它是時間長河中永恒的一瞬。我們都注定要廝守在時間的無限綿延之中。[4]

師者和兒童的教學關系，既是棲息居住，也是往返流連。在上圖③中，當師者和兒童各奔前途，達到目的地（A或B）時，按照小學相遇問題的模型，他們又會折返而回，終究還會遇見在一起的。

童年有著自身的內在價值，作為人一生中最深的年輪，最初的精神胚芽，最基礎的根莖，必將影響、伴隨，并默默滋養著人的一生。教師以及成人所要做的，就是把兒童真正當作一個人、一個與自己平等的人來看待，把孩子的自由和權利還給他們；經常俯下身去，帶著欣賞的心態，聆聽孩子的話，關注他們做的事，陪在孩子身邊，卻要力爭“隱身”，只在他們需要和迷茫的時候“現形”。于是我們將發現：兒童的一個眉眼情態，一舉手一投足，某種言說的方式，某種突出的才干，都留有我們關心的痕跡——就在這難以計數的若干次遇見和微妙的小事情中，我們見證了孩子的學習和生長。endprint

三、教學的關心價值取向

重要的不是在辭藻和意蘊間尋找某種暗示，而是要養育教師獨立思考的習慣和關心的價值取向。也許，我們并不能將哲學、美學方面的思考體悟顯性于每一節課中，但我們內心始終葆有的關心、謙遜和敬畏之情，會使我們的課堂教學立意更高，饒有余味，惠及兒童。

何謂兒童？什么是教育？加拿大教育哲學家馬克斯·范梅南給出了最值得回味和咀嚼的理解：“看待兒童其實就是看待可能性，一個正在成長過程中的人。教育學就是迷戀他人成長的學問。” [5]可能性，多么美好的一個教育隱喻！它激起了我們對教育的無限向往和遐想。孩子是自由成長中的人，充滿著不確定性和可塑性，他們的稚嫩和美好，激起了我們的關心、呵護之情。教育，使我們的心想著、向著孩子。一個始終滿懷期待，關注著可能性，迷戀著兒童成長，佇立在講臺邊的教師形象，該有多么溫暖和光輝啊！

蘇教版數學四年級上冊第六單元學習的主題是“可能性”。一方面我們需要理解其內容的數學意義，另一方面我們亦可隱約地感受到其中一直存有的關心兒童生長的深意。我們希望從下面的案例中獲得一些啟示。

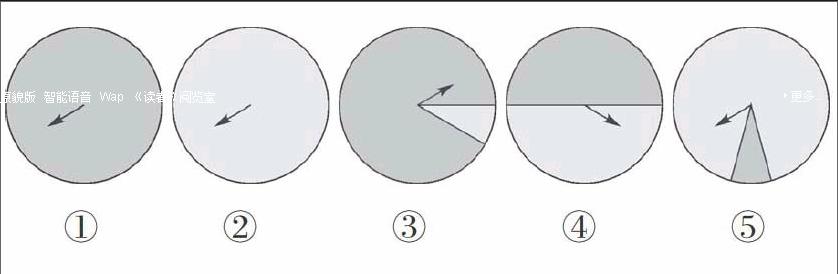
某商場讓顧客摸獎，轉動轉盤，指針落在深色區域中獎（如下圖）。下面幾個轉盤，分別轉動它們，中獎的可能性有多少？如果你是商場經理，哪個轉盤符合你的心意？

生：①號轉盤當然是百分百地獲獎，②號轉盤不可能獲獎，③號轉盤獲獎的可能性比較大，④號轉盤獲獎和不獲獎的可能性相等，⑤號轉盤獲獎的可能性比較小。

生1：如果我是商場經理，我選③號轉盤，讓獲獎的可能性大一些，吸引顧客到我們商場來買東西。

師：很有商業頭腦的商場經理。

生2：如果我是商場經理，我選④號轉盤。這樣，獲獎與不獲獎的可能性相等，既能吸引顧客，又能保證損失不會很多。

師：既考慮獲獎的可能性，又考慮到自己的損失。你想事情比較周全。

生3：我覺得可以把獎品的價值降低些，增加獲獎的可能性，吸引顧客的眼球。選擇③號轉盤比較好。

生4：受前面同學的啟發，我選①號轉盤，人人都能獲獎。

生5：要是獎品不是很貴重，都能獲獎對顧客也沒有什么吸引力。相反，我就覺得在⑤號轉盤上設置大獎，比如手機、電腦等，即使獲獎的可能性小，也能吸引眼球。

生6：我也是受大家發言的啟發。如果我是經理，我要重新設計這個獲獎的轉盤。把轉盤劃分成幾個區域：獲大獎的，獲普通獎的，獲一些小獎的，還有不獲獎的。這樣，就更能吸引顧客了！

師：好，那我們就一起來設計這個轉盤，讓它符合自己的心意！

……

以上授課內容是基于教材的改編。和教材比對，增改了兩個地方：一是創設了轉盤摸獎的情境，二是增設了“如果你是商場經理”的開放性問題。雖是些許改編，學生收獲卻頗豐。

教師該怎樣看待兒童？“可能性”的隱喻給予我們很多的啟示。兒童是正在生長的人，但不是成人，教育的目的也不是讓其變為成人。兒童的生長其實是一件充滿風險的事情，那是因著他們的稚嫩和極強的可塑性。就像美國詩人惠特曼寫的那樣：“有一個孩子每天向前走去∕他看見最初的東西∕他就變成那東西∕如果是早開的紫丁香∕那么它就會變成孩子的一部分∕如果是雜亂的野草∕那么它也會變成∕這個孩子的一部分。”教育教學該有的關心和濡染，就是要擴大其“獲獎區域”，增加其“獲獎”、自由與健康生長的可能性。

教師該怎樣關心兒童？兒童不是一張白紙，任人涂抹，而是帶著各自的精神底色走進學校和課堂的。他們有著無人能夠完全預測的潛能，有自己的未來和成長軌跡，就像瑞士教育家裴斯泰洛齊說的那樣：“人類極大的美德是能夠等待，不慌不忙，直至一切成熟。”上述案例中，成人的眼光中的標準答案是③或④，可在孩子們的眼里心里，就有著不同的角度了，誰又能認為他們說得沒有道理呢？教師要做的，就是關心和守望著“可能性”的發生與發展，呵護童真，順著兒童的天性而為。

參考文獻：

[1]內爾·諾丁斯.學會關心：教育的另一種模式[M].于天龍，譯.北京：教育科學出版社，2014：1.

[2]龍應臺.目送[M].桂林：廣西師范大學出版社，2014：10.

[3][4]馬丁·布伯.我與你[M].陳維剛，譯.北京：商務印書館，2013：34.6.

[5]馬克斯·范梅南.教學機智——教育智慧的意蘊[M].李樹英，譯.北京：教育科學出版社，2001：1.18.endprint