Bergman-Sobolev空間上Toeplitz算子的本性范數

何　莉， 曹廣福

(廣州大學 數學與信息科學學院， 廣東 廣州　510006)

?

Bergman-Sobolev空間上Toeplitz算子的本性范數

何莉， 曹廣福

(廣州大學 數學與信息科學學院， 廣東 廣州510006)

文章研究了Bergman-Sobolev上Toeplitz算子的某些性質，主要通過該類算子的符號函數在邊界處的行為計算了它們的本性范數.

Bergman-Sobolev空間; Toeplitz算子; 本性范數

0　Introduction

Denote by R the real number set, N the natural number set and N*the positive integer set.

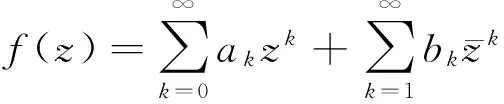
Forβ∈R and 1≤p<+∞, the Sobolev space Lβ,pis the completion of all functionsf∈() for which

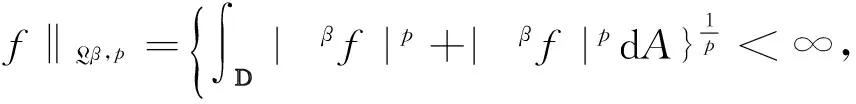
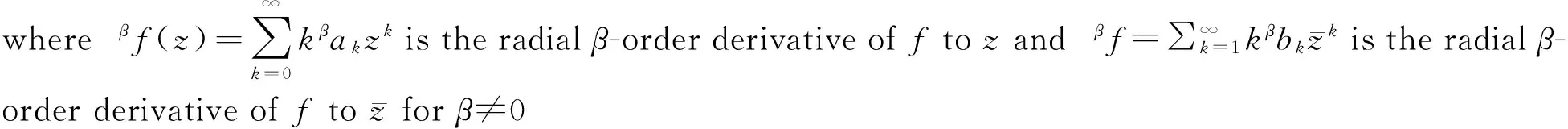
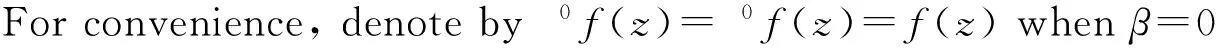
Forp=2, the space Lβ,2is a Hilbert space with the inner product

?f∈Lβ,2,g∈Lβ,2.

Here,L2denotes the usual Lebesgue spaceL2(,dA) and the notation·,·L2denotes the standard inner product inL2.

Whenp=+∞, the corresponding Sobolev space is written as

Lβ,∞={f:→

with ‖f‖Lβ,∞=‖βf‖L∞+‖f‖L∞.SinceeachfunctioninLβ,∞can be extended to a continuous function on the closed unit disc} by Sobolev’s embedding theorem (see Theorem 5.4 of Ref.[1]), we will use the same notation between a function in Lβ,∞and its continuous extension onin this paper.

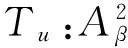
Tuf=P(uf)

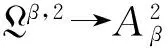
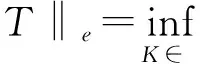
In this paper, we calculate the essential norm of Toeplitz operators on Bergman-Sobolev space with positive integer derivative in terms of the boundary value of the corresponding symbol.

1　Essential norm of Toeplitz operators

Lemma 1For eachλ∈

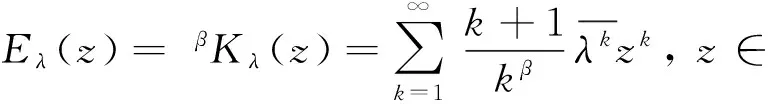
Proof. See Proposition 3.2 of the paper given in footnote*HE L, CAO G F. Toeplitz operators on Bergman-Sobolev space with positive integer derivative[J]. Sci China Math Ser A, 2016, preprint..

Proof. See Lemma 3.3 of the paper given in footnote①.

Proof. See Lemma 3.4 of the paper given in footnote①.

Lemma 4Letu,v∈Lβ,∞andζ∈. Then, limλ→ζ).

Proof. See Lemma 3.5 of the paper given in footnote①.

Theorem 1Letu∈Lβ,∞,β∈N*. Then, ‖Tu‖e=maxζ∈}|u(ζ)|.

Proof. Setρ=maxζ∈|u(ζ)| for simplicity. Choose some pointη∈so thatu(η)=ρ. For anyK∈,

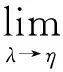
byLemma4withv=1, this indicates ‖Tu‖e≥maxζ∈|u(ζ)|.

②LEE Y J. Compact sums of Toeplitz products and Toeplitz algebra on the Dirichlet space[J]. Tohoku Math J, preprint,2016.

for everyj>j0.

Moreover, sinceuis continuous on, we can choose somer∈(0,1) such that |u(z)|≤ρ+εfor everyr<|z|<1.

asj→∞. Since

for eachj∈N*, it is not difficult to get that

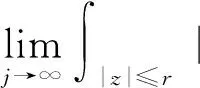
∫|z|≤r|βfj|2dA<ε

for everyj>jβ. Notice that

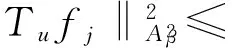
for eachj∈N*, where

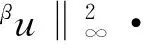
asj→∞, we have

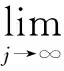
Direct calculation follows that

(1)

by Minkowski inequality. Since

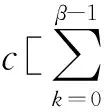
by Cauchy-Schwarz inequality, where

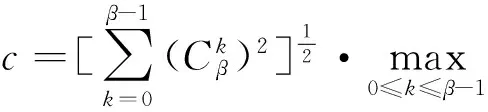
is a positive number, there exists an integerj*≥0 such that

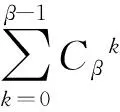
(2)

whenj>j*because ‖kfj‖A2→0 for each integer 0≤k≤β-1 asj→∞ by Lemma 3. Furthermore, for everyj>jβ,

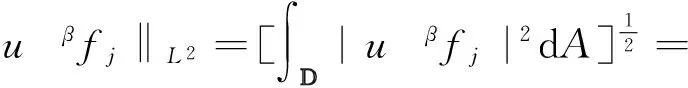
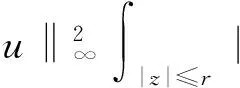
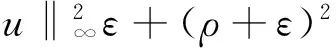
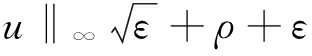
(3)

Then, by combining the inequalities (1), (2) and (3), we have

‖β(ufj)‖L2≤‖

asj>max{jβ,j*}. This implies that

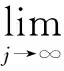
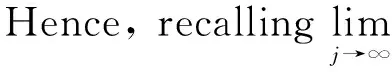
2　Main result

The main result is the calculation of the essential norm of the Toeplitz operators in terms of the boundary value of their corresponding symbols. That is

Theorem 2Letu∈Lβ,∞,β∈N*. Then,

‖Tu‖e=maxζ∈|u(ζ)|.

AcknowledgmentsThe authors would like to thank professor YOUNG J L in Korea for helpful discussions.

[1]ADAMS R A. Sobolev spaces[M]∥A subsidiary of Harcourt Brace Jovanovich, Pure and applied mathematics. New York-London: Academic Press, 1975:65.

[2]COHN W S, VERBITSKY I E. On the trace inequalities for Hardy-Sobolev functions in the unit ball ofn[J]. Indian Univ Math J, 1994, 43(4): 1079-1097.

[3]BRUNA J, ORTEGA J M. Interpolation along manifolds in Hardy-Sobolev spaces[J]. J Geom Anal, 1997, 7(1): 17-45.

[5]CASCANTE C, ORTEGA J M. Carleson measures for weighted Hardy-Sobolev spaces[J]. Nagoya Math J, 2007, 186: 29-68.

[6]TCHOUNDJA E. Carleson measures for the generalized Bergman spaces via aT(1)-type theorem[J]. Ark Mat, 2008, 46(2): 377-406.

[7]CHO H R, ZHU K H. Holomorphic mean Lipschitz spaces and Hardy-Sobolev spaces on the unit ball[J]. Complex Var Elliptic Equ, 2012, 57(9): 995-1024.

[8]CAO G F, HE L. Fredholmness of Multipliers on Hardy-Sobolev spaces[J]. J Math Anal Appl, 2014, 418(1): 1-10.

[9]CAO G F, HE L. Hardy-Sobolev spaces and their multipliers[J]. Sci China Math Ser A, 2014, 57(11): 2361-2368.

[10]HE L, CAO G F. Composition operators on Hardy-sobolev spaces[J]. Indian J Pure Appl Math, 2015, 46(3): 255-267.

[11]HE L, CAO G F. Toeplitz operators with unbounded symbols on Segal-Bargmann space[J]. J Math Res Appl, 2015, 35(3): 237-255.

[12]HONG C K. On the essential maximal numerical range[J]. Acta Sci Math, 1979, 41: 307-315.

【責任編輯： 周全】

date: 2016-01-05;Revised date: 2016-04-18

s: National Natural Science Foundation of China (11501136); The key discipline construction project of subject groups focus on Mathematics and information science in the construction project of the high-level university of Guangdong Province (4601-2015); Guangzhou University (HL02-1517) and (HL02-2001)

Essential norm of Toeplitz operators on Bergman-Sobolev space

HE Li, CAO Guang-fu

(School of Mathematics and Information Sciences, Guangzhou University, Guangzhou 510006, China)

In this paper, we study some properties of Toeplitz operators on the Bergman-Sobolev space. Mainly, we calculate the essential norm of these operators in terms of the boundary value of their corresponding symbols.

Bergman-Sobolev space; Toeplitz operator; essential norm

O 177.1Document code: A

1671- 4229(2016)04-0018-04

O 177.1

A

Biography: HE Li(1986-), female, Doctor of science. E-mail: helichangsha1986@163.com.