基于Dijkstra最短路徑算法的教育裝備更新問題

◆曹瑩瑩　李慧

基于Dijkstra最短路徑算法的教育裝備更新問題

◆曹瑩瑩李慧

隨著教育水平的不斷提升，教育領域教育裝備的投入步伐大大加快，設備的更新換代越發頻繁。為了最大限度發揮教育裝備的功能，保障優質教學，學校每年都要對教育裝備進行更新與維護且使總費用最小化。首先建立教育裝備更新數學模型，闡明如何更新教學中的設備使總費用最小化，并采用Dijkstra最短路徑算法實現教育裝備的更新。

教育裝備更新；最短路徑；Dijkstra算法

10.3969/j.issn.1671-489X.2016.16.001

隨著計算機技術和教育信息化的發展，具有先進技術含量的教育裝備在教育教學中得到廣泛應用，教育裝備的分配、管理、購置和維修等問題也隨之變得更為復雜。先進的教育裝備不僅能為學校提供良好的教學環境和豐富的教學資源，還能鍛煉學生的實踐能力和創新思維。因此，在當前的教育教學中，先進的教育裝備已逐漸成為教學過程中不可或缺的重要條件。

教育裝備必須經歷一個管理知識量化的過程，才能從經驗管理向科學管理過渡，使得管理工作成為可預測、可測量、可重復、可控制的科學管理過程［1］。為此，就必須把管理學、運籌學等理論和方法引入教育裝備管理中來，以科學方法解決實際問題。目前我國的經濟發展水平和社會發展階段共同決定了下發到各個學校的教育經費的有限性，在滿足日常的教育需求和科研工作的前提下，學校要考慮教育裝備的更新成本以及繼續使用舊裝備的維修費用等問題，盡可能地壓縮教育裝備的更新費用是教育裝備管理工作中面臨的難題。本文以解決教育裝備更新問題為切入點，應用基于Dijkstra的最短路徑算法實現其總費用最小化的求解，為教育裝備資源分配工作提供科學依據。

1　算法的基本概念

圖論的起源可以追溯到瑞士數學家（E.Euler）在1736年發表的一篇解決“哥尼斯堡七橋問題”的論文。在自然界和人類社會中，大量的事物以及事物之間的關系，常可以用圖來描述［2］。隨著現代生產和科學技術的迅猛發展，特別是計算機的出現和互聯網的普及，使圖論方法得以快速擴展，圖論已成為運籌學中引人注目的重要分支，滲透到物理學、化學、電工學、管理學、控制論、信息論等諸多學科［3-4］。

最短路徑問題是圖論中應用最廣泛的問題之一。許多實際問題求最優解可以使用這個模型，如設備更新、管道鋪設、選址布局等。所謂最短路徑是指在一個連通圖中，求從某一個指定結點（起始點）到另一個指定結點（終點）的距離最短的路徑，即：尋求賦權圖中任意兩點之間的最短路徑。這里的最短路徑只是圖中邊權數的代名詞，在解決實際問題時，它可以是時間、費用等其他不同含義的量［5］。

Dijkstra算法是解決最短路徑問題的常用算法之一，適用于所有權wij≥0情況下求指定兩點間的最短路徑，目前已經被廣泛應用。在這里可以把教育裝備更新問題抽象為賦權有向圖，利用Dijkstra算法進行求解，從而得到某段時間內總費用最少的路徑，為教育裝備的更新提供最優化方法。

圖的相關概念

1）圖（Graph），即偶對（V，E），記作G（V，E）。其中，V是頂點（Vertex）的集合，E是邊的集合。

2）有向圖（Digraph），即有序偶對（V，E），記作D=（V，A）。其中，V是頂點（Vertex）的集合，A是弧的集合。換言之，有向圖就是所有邊都具有一定方向的圖。

3）賦權圖（Weighted graph），即在圖G（V，E）中，每一條邊（vi，vj）均有一個數wij與之對應，數wij即為邊（vi，vj）的權值。

4）連通圖（Connected graph）：設vi和vj為圖G中的兩個點，若存在從點vi到點vj的鏈，則稱vi和vj是連通的；若圖G中的任意一對頂點均連通，則圖G被稱為連通圖。

Dijkstra算法的基本思想Dijkstra算法的基本思路是把圖中的全部頂點分為兩組，令V表示已標記最短路徑的頂點集合，其余未標記最短路徑的頂點集合為；初始狀態時，集合V中只含有起始點s，中含有除起始點s之外的其余各頂點，此時各頂點的當前最短路徑為起始點到該節點的弧上的權值；然后不斷地從集合中選取到頂點集V中各頂點的路徑長度最短的頂點u加入到集合V中，集合V中每加入一個新的頂點u，都要分別修改已標記集合V和未標記集合中的頂點。集合中各頂點新的最短路徑長度值為原來的最短路徑長度值加上u到該頂點的路徑長度值中的較小值。重復此過程，直到集合V包含圖中所有頂點（即所有頂點都被標記）為止。

定義dij是圖中頂點i和j之間的距離，即：

給定賦權有向圖D=（V，A），采用Dijkstra算法求從起始點s到終點t的最短路徑的具體步驟如下。

1）從起始點s出發，每個節點都進行標記，記作Lij；其中Lij是從節點i到節點j的最短路徑。Lss=0（從頂點到其本身的最短路徑是零路——沒有弧的路［6］，其長度為0），將點s標記為“0”，表示點s已被標記。令s∈V，其余各點均屬于。

2）從起始點s出發，找到與點s相鄰且距離最短的點i，將Lsi=Lss+Lsi的值作為節點i的標記，表示節點i已被標記。令（s，i）∈V，其余各點均屬于。

3）找出所有與已標記點相鄰的未標記的點（即廣度優先搜索），若Lsj=min｛Lss+dsj，Lsi+dij｝，則給點j標記。令（s，i，j）∈V，其余各點均屬于。

重復操作以上步驟共n-1次，由此求得從s到圖上其余各頂點的最短路徑［7］。

2　實例應用

建立數學模型本文用一個簡單的數學模型來說明教育裝備更新問題。假設某學校的電教實驗室使用一種電教裝備，每年的年初，管理員都要決定是繼續使用舊裝備，還是購買新裝備。如果繼續使用舊裝備，就要支付一定的維修費用，隨著裝備的老化，維修費也會隨之上升（如表1所示）；如果購置新裝備，就要付購置費和相應較少的維修費（如表2所示）；如果購置新裝備或不想繼續維修，打算把舊裝備賣掉折舊，就可以獲得部分折舊費，隨著裝備的老化破碎，折舊費會隨之減少（如表2所示）。試制訂一個4年的電教裝備更新計劃，使總支出最少。

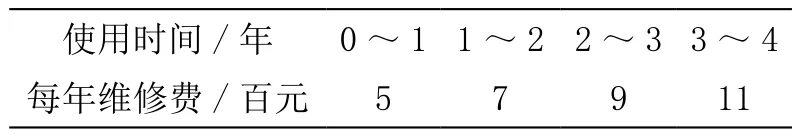
表1　4年內裝備維修費

表2　4年內裝備購置費和折價費

顯然，可供選擇的裝備更新方案是很多的，但是每種方案花費的總費用不同。

如每年都購買一臺新的裝備（即使用一年就更新），則其購置費是27+28+29+30=114（百元）；而每年支付的維修費用是5（百元），4年維修費合計是20（百元），于是4年總的支付費用是114+20=134（百元）；再減去4年中每年的裝備折舊費24+20+17+14=75（百元），最后為59（百元）。

又如決定第一年購買的裝備一直使用到第四年年底，則4年支付費用總和為第1年的裝備購置費加上四年中每年的維修費，合計為27+5+7+9+11=59（百元），再去掉第四年年底的裝備折舊費14（百元），為44（百元）。

如何制訂方案，使得總支付費用最小呢？可以把這個問題轉化為賦權有向圖（如圖1所示），然后轉為求解最短路徑問題。

令vi表示第i年年初購進一臺新裝備（i=1，2，3，4，5），v5表示第四年年底。

（vi，vj）表示第i年購進的新裝備一直使用到第j年年初（即第j-1年年底）（j=2，3，4，5）。

wij表示弧（vi，vj）所賦的權值，即第i年購置的裝備的費用加上從第i年使用到第j年年初（即第j-1年年底）的維修費，再去除相應折舊費的最終結果。

每條弧的權值可按照已知資料（如上給出的兩張表）計算出來，結果如表3所示。如（v1，v3）是第1年年初購進裝備（支付購置費27），一直使用到第2年年底（支付維修費5+7=12），如果第3年年初賣掉折舊（可得折舊費20），故（v1，v3）上的權值為19。

根據得出的每條邊的權值，進而將裝備更新問題轉化為賦權連通圖，如圖2所示。這樣制訂一個最優的裝備更新計劃的問題，就等價于尋求從v1到v5的最短路徑問題。

Dijkstra算法的實現用Dijkstra算法求圖2中從v1到v5的最短路徑，此算法結果就對應著總花費最低的裝備更新計劃。

圖1　裝備更新問題的有向圖

表3　所有弧的權值wij單位（百元）

圖2　裝備更新問題的賦權連通圖

1）從點v1出發，對其標“0”。令v1∈V，其余各點均屬于。

2）與點v1相鄰的未標號點有v2、v3、v4和v5四個點，由于min｛0+8，0+19，0+31，0+45｝=8，故v2點標號為“8”。令（v1，v2）∈V，其余各點均屬于。

3）與點v1和點v2相鄰的未標號點有v3、v4和v5三個點，由于min｛v1：0+19，0+31，0+45｝=19，min｛v2：8+13，8+23，8+35｝=21，取min｛19，21｝=19，故v3點標號為“19”。令（v1，v2，v3）∈V，其余各點均屬于。

4）與點v1、點v2和點v3相鄰的未標號點有v4和v5兩個點，由于min｛v1：0+31，0+45｝=31，min｛v2：8+23，8+35｝= 31，min｛v3：19+17，19+23，19+27｝=36，取min｛31，31，36｝=31，故v4點標號為“31”。令（v1，v2，v3，v4）∈V，其余各點均屬于。

5）與點v1、點v2、點v3和點v4相鄰的未標號點僅有v5一個點了，由于min｛v1：0+45｝=45，min｛v2：8+35｝=43，min｛v3：19+27｝=46，min｛v4：31+21｝=52，取min｛45，43，46，52｝=43，故v5點標號為“43”。此時所有頂點均得到標號，算法結束。

6）逆推可得到頂點v1到終點v5的最短路徑：v1→v2→v5，最短路徑長為43。

因此，總費用最少的電教裝備更新方案為：第一年購買電教裝備，使用1年；第二年年初購買新的電教裝備，使用3年，直至第四年年底，總費用最少是43（百元）。

3　結語

教育裝備更新問題是學校在教育裝備管理過程中常遇到的問題，在有限的教育經費下，何時更新裝備才能保證教育經費花費最低，是學校要考慮的重要因素。因此，學校各院系的教育裝備管理者需要運用科學的方法去解決裝備更新的實際問題。Dijkstra算法是單源最短路徑的代表性算法，可以求出其中任一點到其余各點的最短路徑，能得出最短路徑的最優解。但是它遍歷計算的節點很多，所以效率低。本文應用Dijkstra算法于裝備更新問題，高科技含量的教育裝備更新較快，以年為節點，節點數目不會很多，可以很好地運用Dijkstra算法，通過不斷地迭代做出在當前看來最好的選擇，最終找到問題的最優的解決方案。

［1］艾倫，姚玉琴，等.教育裝備從經驗管理走向科學管理［J］.中國教育技術裝備，2009（32）：17.

［2］胡運權，郭耀煌.運籌學教程［M］.2版.北京：清華大學出版社，2003：252-253.

［3］辛宇.基于運籌學圖論的物流網絡優化研究［J］.中國外資，2011（6）：125-127.

［4］蔣智凱.淺談運籌學教學［J］.重慶科技學院學報：社會科學版，2010（24）：176-177.

［5］李慧.教育裝備運籌規劃［M］.北京：北京大學出版社，2010：100-116.

［6］樂陽，龔健雅.Dijkstra最短路徑算法的一種高效率實現［J］.武漢測繪科技大學學報，1999（3）：209-212.

［7］許永昌，王甲琛.基于最短路徑問題在企業設備更新中的應用［J］.山東英才學院學報，2006（4）：64-65.

圖2

Educational Equipment Update Problem based on Dijkstra's Shortest Path Algorithm

//CAO Yingying， LI Hui

With the rising levels of education， in the fi eld of education greatly accelerate the pace of investment in educational equipment，more frequent replacement of equipment. In order to maximize the function of educational equipment to ensure the quality of teaching，the schools update and maintain educational equipment every year to minimize the total cost. Firstly， the article builds the mathematical models of educational equipment update and illustrates how to update educational device， minimizing the total cost. And， the article uses the Dijkstra's shortest path algorithm to realize the educational equipment update.

educational equipment update； the shortest path； Dijkstra algorithm

G650

A

1671-489X（2016）16-0001-03

作者：曹瑩瑩，首都師范大學教育技術系，研究方向為教育傳播理論與技術；李慧，博士，首都師范大學教育技術系副教授、碩士生導師，研究方向為教育裝備、教育技術學（100048）。