四色定理的美妙證法

程中戰

四色定理命題：

任何一張地圖只用四種顏色就能使任意兩個相鄰的國家著上不同的顏色。

證明：（本文用1 2 3 4代表四種顏色）

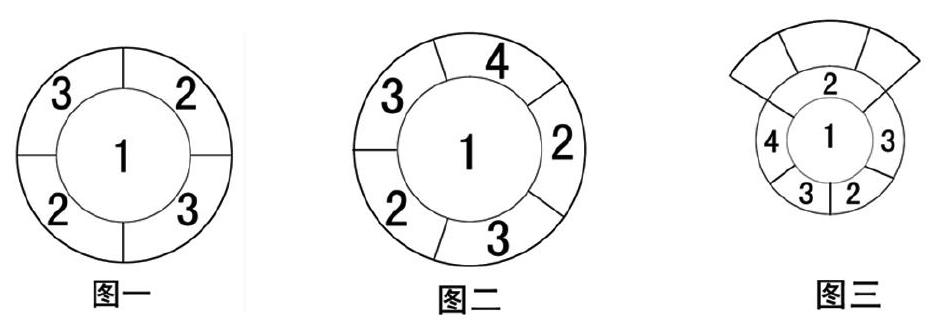
公理1：設平面內一個區域（中心區）的周圍有n個相鄰的區域（鄰區），當n為奇數時，所有鄰區最多只用三種顏色（n為偶數時只用兩種顏色）即可使包括中心區在內的所有兩兩相鄰的區域著上不同的顏色（中心區為第四種顏色）。這種現象稱為圓環布局，見圖一圖二。

在平面內可以任何一個區域為中心區，在它周圍沒有鄰區的線段（或曲線段）上布設若干個鄰區，使它們符合新的圓環布局，這條線段（或曲線段）稱為空白邊，而已經著色的所有區域構成一個不規則（或規則）的版塊，這個版塊的外邊緣是由若干條空白邊相連結的不規則環線，稱這個環線為空白圈。

公理2：即公理1的推論，任何一條空白邊上布設的k個鄰區最多只用三種顏色即可填充，就能使其對應的中心區及原有的鄰區符合圓環布局。

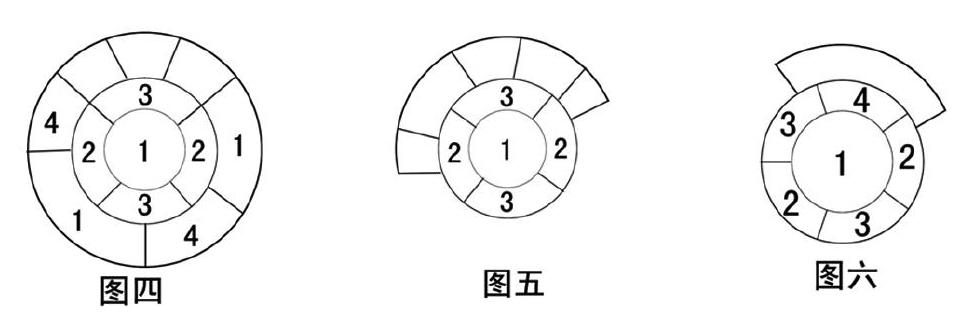
一條空白邊的兩個端點處有四種情況（如圖三圖四）：

1.一端有鄰區另一端無鄰區；2.兩端都無鄰區；3.兩端都有鄰區且同色；4.兩端都有鄰區且異色。據公理1公理2知，以上四種情況，一條空白邊上最多只用三種顏色，加上中心區的顏色，共用四種顏色，就能使這個中心區周圍的新舊鄰區符合圓環布局。同理，無論單條還是多條空白邊上布設新的鄰區，都符合圓環布局，連續空白邊的填充是若干條空白邊填充的合成（如圖五圖六）。這時空白圈向周圍擴展，著色版塊面積增加，就象漣漪、樹木的年輪，又象是中心開花，花瓣層層向周圍擴展。

任何一個不規則的空白圈都等價于一個圓，因而，任何一個空白圈內緣的所有區域相連結的圖形都等價于一個圓環，故，空白圈內緣上的所有區域最多只用三種顏色即可填充。所以，空白圈外緣上任意弧長的一個鄰區（即若干條連續空白邊的公共鄰區）可用第四種顏色填充（如圖六）。

由上可知，四色定理成立。四色定理適合于一個充分大的平面及一個封閉的曲面（如球面）。