拉格朗日中值定理反問題存在性及存在不可導點的相關結論探討
熊駿
(長江大學信息與數學學院,湖北 荊州 434023)
?
拉格朗日中值定理反問題存在性及存在不可導點的相關結論探討
熊駿
(長江大學信息與數學學院,湖北 荊州 434023)
從幾何意義出發研究拉格朗日中值定理的反問題,得到了拉格朗日中值定理反問題的2個存在性結論。此外,還探討了函數有不可導點情形下拉格朗日中值定理的相關結論,豐富了拉格朗日中值定理的結果。
拉格朗日中值定理;反問題;不可導點
拉格朗日中值定理[1~5]是微分中值定理的核心,在數學分析的理論及應用中有很重要的作用。拉格朗日中值定理具體表述如下:
若函數f(x)在[a,b]上連續,在(a,b)內可導,則存在ξ∈(a,b),使得:
其幾何意義是在曲線L:y=f(x)上存在點P(ξ,f(ξ)),曲線在該點的切線的斜率等于曲線上兩點A(a,f(a)),B(b,f(b))確定直線AB的斜率。
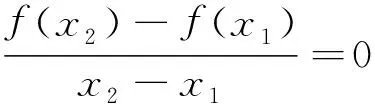
為此,筆者考慮增強函數f(x)的條件,使得上述拉格朗日中值定理反問題的存在性成立。另外,還考慮了若函數f(x)在[a,b]上連續,在(a,b)有不可導點的情形下拉格朗日中值定理的相關結論。
1 拉格朗日中值定理反問題的2個存在性結論
定理1設函數f(x)在[a,b]上二次可導,且f″(x)≠0(x∈[a,b]),則對任意的ξ∈(a,b),存在c∈[a,b],使得:
或
證明因f″(x)≠0(x∈[a,b]),由導數的介值定理可知,f″(x)(x∈[a,b])不可能變號,不妨設f″(x)>0(x∈[a,b]),于是f′(x)在[a,b]上嚴格單調遞增。因此,對任意的ξ∈(a,b),有:
f′(a) 由定理1的證明中,二階導數的作用可以適當減弱條件為f′(x)在[a,b]上嚴格單調,從而得到如下推論。 推論1設函數f′(x)在[a,b]上嚴格單調,則對?ξ∈(a,b)存在c∈[a,b],使得; 或: 定理2設函數f(x)在[a,b]上二次可導,則對?ξ∈(a,b),若f″(ξ)≠0,存在x1,x2∈(a,b),使得x1<ξ 證明不妨設f″(ξ)>0,由極限的局部保號性知,存在ξ的某鄰域,在該鄰域內f′(x)單調遞增。即存在δ>0,當x∈(ξ-δ,ξ)時,f′(x) 分析f″(ξ)≠0在證明中的作用,由定理2可以得到如下推論。 推論2設函數f(x)在[a,b]上連續,在在(a,b)內可導,則對任意的ξ∈(a,b),若ξ不是f′(x)的極值點,則存在x1,x2∈(a,b),使得x1<ξ 證明不妨設a f(c1)-f(a)=f′(ξ1)(c1-a),ξ1∈(a,c1) f(c2)-f(c1)=f′(ξ2)(c2-c1),ξ1∈(c1,c2) ? f(b)-f(cN)=f′(ξN+1)(b-cN),ξN+1∈(cN,b) 以上各式2邊除以b-a再相加得到: 定理3中, N=1即為拉格朗日中值定理。 f(b)-f(c1)=f′(ξ1)(b-c1),ξ1∈(c1,b) f(c1)-f(c2)=f′(ξ2)(c1-c2),ξ1∈(c2,c1) ? f(cn-1)-f(cn)=f′(ξn)(cn-1-cn),ξn∈(cn,cn-1) 以上各式兩邊除以b-a再相加,再取極限n→∞,得到: 拉格朗日中值定理的幾何意義為思考某些問題提供了思路,加強函數的條件可以得到一些拉格朗日中值定理反問題的存在性結果。在今后的研究中,還可以通過加強函數的條件考慮拉格朗日中值定理中點的存在個數問題。 [1]華東師范大學數學系.數學分析(上冊) [M]. 第3版.北京:高等教育出版社,2005. [2]劉三陽,于力,李廣民.數學分析選講[M].北京:科學出版社,2006. [3]同濟大學數學系.高等數學(上冊)[M]. 第6版.北京:高等教育出版社,2006. [4]四川大學數學系.高等數學(第一冊)[M]. 第2版.北京:高等教育出版社,1989. [5]冉兆平.微積分[M]. 第2版.上海:上海財經大學出版社,2008. [編輯]張濤 2016-04-20 熊駿(1967-),男,碩士,副教授,現主要從事基礎數學方面的教學與研究工作;E-mail:cjdxxj@163.com。 O172.1 A 1673-1409(2016)22-0060-04 [引著格式]熊駿.拉格朗日中值定理反問題存在性及存在不可導點的相關結論探討[J].長江大學學報(自科版),2016,13(22):60~63.
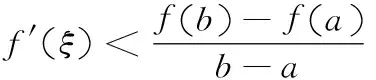

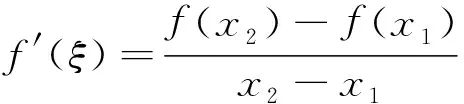
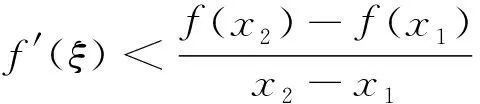
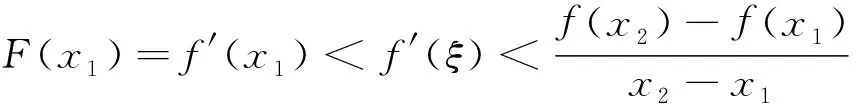
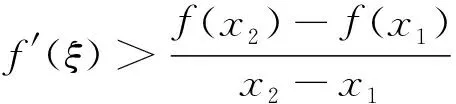
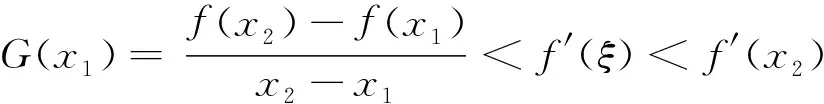
2 存在不可導點情形下拉格朗日中值定理的相關結論
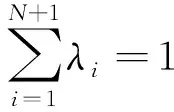
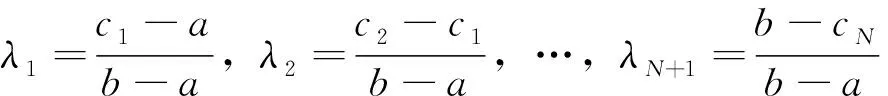
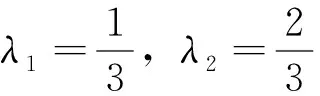
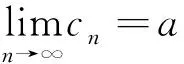
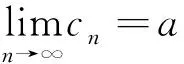
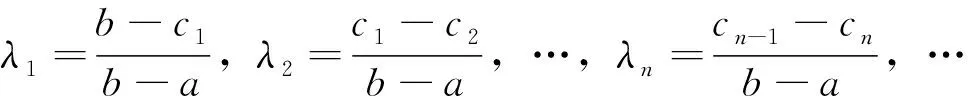
3 結語

