自黏運動繃帶剝離強度力學模型研究

李玉鵬　王　其　劉昌杰　郭超群　劉　波

1.東華大學紡織面料技術教育部重點實驗室(中國) 2.無錫百和織造股份有限公司(中國)

?

產業用紡織品

自黏運動繃帶剝離強度力學模型研究

李玉鵬1王其1劉昌杰2郭超群2劉波2

1.東華大學紡織面料技術教育部重點實驗室(中國) 2.無錫百和織造股份有限公司(中國)

將自黏運動繃帶背部膠層設計為條狀花紋，花紋寬度為2 mm，間隔為1 mm，條狀花紋與寬度方向成一定角度，夾角分別為0°、15°、30°、45°和90°，基于Maxwell模型建立了自黏運動繃帶剝離強度計算式，用于計算和預測此類自黏運動繃帶的剝離強度，計算的剝離強度偏差百分率小于3%。

自黏運動繃帶；剝離強度；模型

自黏運動繃帶是在彈力繃帶基布的背部涂覆一層壓敏膠，直接黏貼于人體皮膚表面，它具有良好的彈性和舒適性，對運動機能增強、運動的損傷防治和康復具有一定輔助作用[1]。目前市場上多數自黏運動繃帶是使用壓敏膠的鋪滿整個基布，導致透汽性較差，剝離強度單一，無法滿足不同年齡人群和人體不同部位的特殊需要。

為此，本研究中采用不連續條狀膠層，使繃帶具有一定的透汽性，通過改變條狀膠層與寬度方向間的夾角，設計了具有不同剝離強度的系列自黏運動繃帶，基于自黏運動繃帶剝離瞬間壓敏膠的拉伸變形，建立此類自黏運動繃帶剝離強度力學模型，用于計算和預測自黏運動繃帶的剝離強度。

1　自黏運動繃帶中壓敏膠黏彈模型分析

自黏運動繃帶的剝離強度為膠接接頭受外力剝離時，在自黏運動繃帶寬度方向單位長度上產生的拉力，是一種線強度。剝離過程中，由于外加負荷的作用，膠黏劑產生黏彈形變，形成不連續的膠束，其180°剝離及剝離界面示意圖如圖1所示。

壓敏膠的黏彈形變應用Maxwell模型[2](一個理想彈簧和一個理想黏壺串聯)分析，模型受力時，彈簧和黏壺的應力與總應力(σ)相同，總應變(ε)為彈簧(ε1)和黏壺(ε2)的應變之和，即

圖1　自黏運動繃帶180°剝離及剝離界面示意圖

本構方程式為

式中：E——彈性模量；

η——黏滯系數。

在此種模型下，當應變保持不變，解微分方程，可得

式中：ε0——t=0時的應變；

τ——常數。

在維持恒定形變時，有應力松弛過程。

當應力保持不變，可得蠕變方程：

當t=0時，有瞬時彈性形變產生。

假設在施加剝離負荷的瞬間，即t→0+時，形成的單根膠束應力與應變的關系為

σ=Eε

(1)

式中：E——壓敏膠彈性模量，MPa；σ——剝離時拉伸成單根膠束時的應力，N/mm2；

ε——剝離時拉伸成單根膠束時的瞬時形變，mm。

2　自黏運動繃帶剝離強度模型建立

本研究中，將自黏運動繃帶背部膠層設計為條狀花紋，花紋寬度為2 mm，間隔為1 mm，條狀花紋與寬度方向成一定角度，夾角分別為0°、15°、30°、45°和90°，如圖2所示。

圖2　膠層花紋示意圖

整片自黏運動繃帶的剝離強度實質上為剝離過程中，撓性材料(運動繃帶基布)作用于膠黏劑，使單位寬度上膠黏劑發生宏觀形變，形成若干根膠束時抵抗外加負荷的應力，即形成的若干膠束黏彈形變的綜合表現。

假設撓性材料自身性能及被黏物(鋼板)的表面粗糙度對剝離強度無影響，膠層厚度不變，剝離瞬間，單位寬度(10 mm)上實際產生剝離作用的剝離有效長度為L(mm)，形成膠束的百分率(剝離時，膠束在剝離線上投影的長度占整個剝離線長度的百分比)為ω(%)。由于前排膠束還未完全與鋼板分離時，后排已有膠束形成，對剝離強度產生影響，形成牽連關系，因此引入修正系數(K)修正，整片自黏運動繃帶剝離強度(P)的計算式表示為

P=KLωEε

(2)

3　自黏運動繃帶剝離強度模型參數確定

3.1形成膠束的百分率(ω)

試驗采用5種不同花紋膠層的自黏運動繃帶，條狀花紋與寬度方向的夾角(θ)分別為0°、15°、30°、45°和90°。表1所示為實際測得的不同角度條狀膠層的剝離有效長度(L)及形成膠束的百分率(ω)。

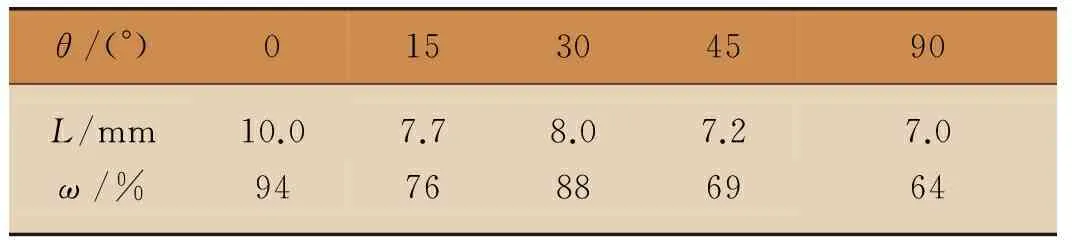
表1　不同角度條狀膠層的L與ω

為了建立剝離有效長度與形成膠束的百分率之間的關系式，以剝離有效長度為自變量，形成膠束百分率為因變量，對其關系進行擬合，所得曲線如圖3所示。

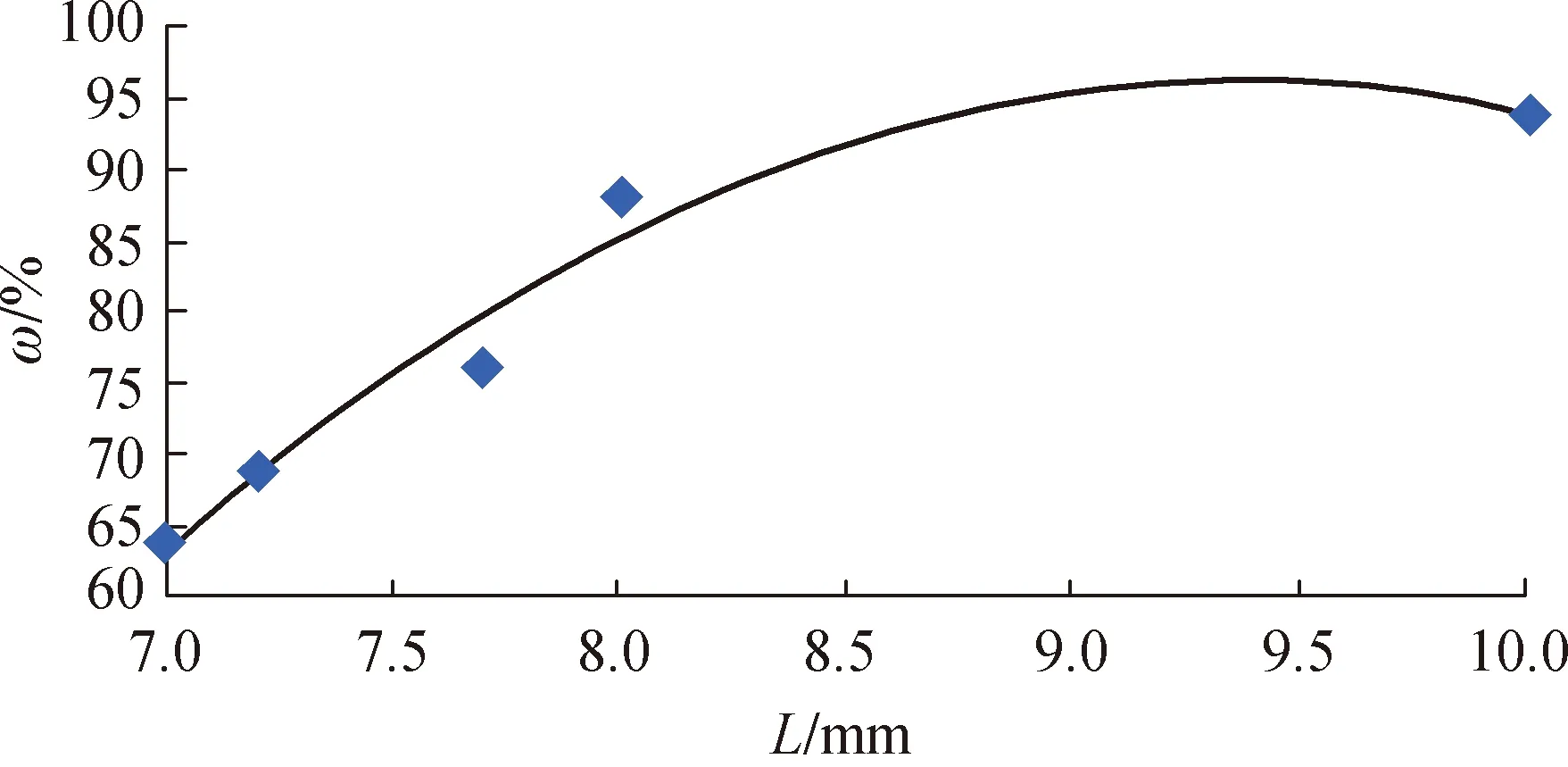
圖3　剝離有效長度與形成膠束百分率的關系

從而得到剝離有效長度與形成膠束的百分率之間的關系式為

ω=-5.7139L2+107.38L-408.26

(3)

3.2修正系數(K)

本研究中使用的膠黏劑為深圳市安固樂科技有限公司提供的丙烯酸酯壓敏膠，其彈性模量為0.3 MPa。在180°剝離過程中，假設被拉伸的膠束均為圓柱體，且其應變ε取值為3 mm，當修正系數K=1時，表示剝離過程中只有一排膠束被拉起，且其應變值相等，即只有極窄的寬度對剝離強度產生影響。將以上參數及式(3)代入式(2)中，可得K=1時，理論剝離強度(PL)(表2)。

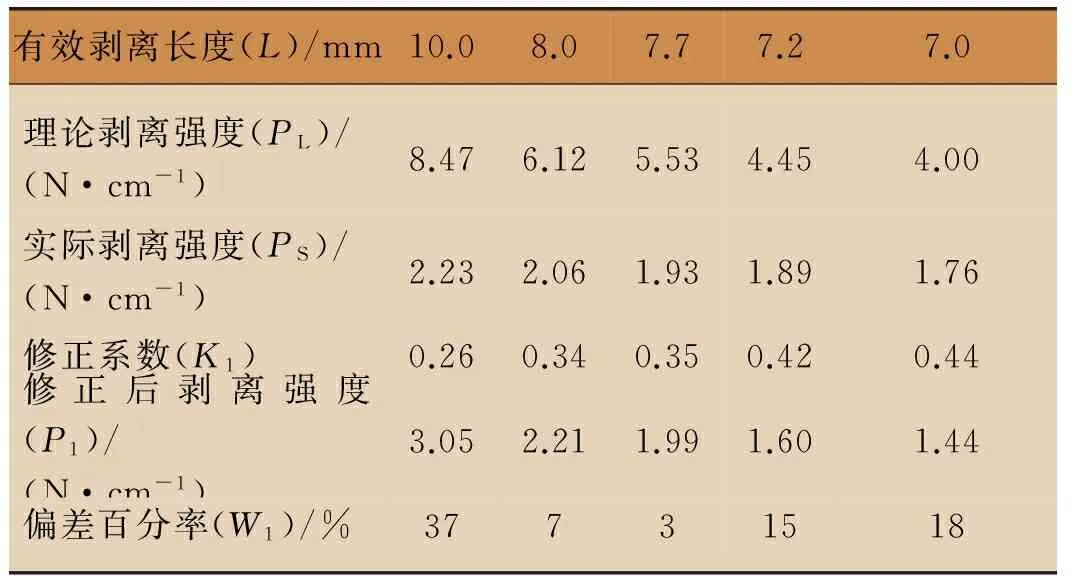
表2　數據綜合表

按照GB/T 2792—1998《壓敏膠黏帶180°剝離強度試驗方法》[3]，試樣在25 ℃條件下放置20 min，測得5組不同花紋膠層的實際剝離強度(PS)(表2)。

根據試驗結果，利用自黏運動繃帶的實際剝離強度(PS)與理論剝離強度(PL)的比值計算修正系數(K1)：

(4)

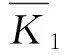
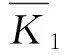
(5)

為驗證這種人為設定的有效性，可通過計算該約定下自黏運動繃帶理論剝離強度相對于實際剝離強度的偏差百分率(W1)：

(6)

計算結果見表2?？梢?，采用式(2)及其相關參數計算此類自黏運動繃帶剝離強度偏差較大，最大偏差達37%，因此計算精度較低。

為提高計算精度，現用SPSS軟件進行二次修正，得到整片自黏運動繃帶剝離強度(P2)的計算式為

P2=4.489+0.485PL

(7)

二次修正后，根據式(4)～式(7)計算得到二次修正后的理論剝離強度(P2)、二次修正系數(K2)、二次修正后的剝離強度(PZ)及二次修正后的偏差百分率(W2)如表3所示。

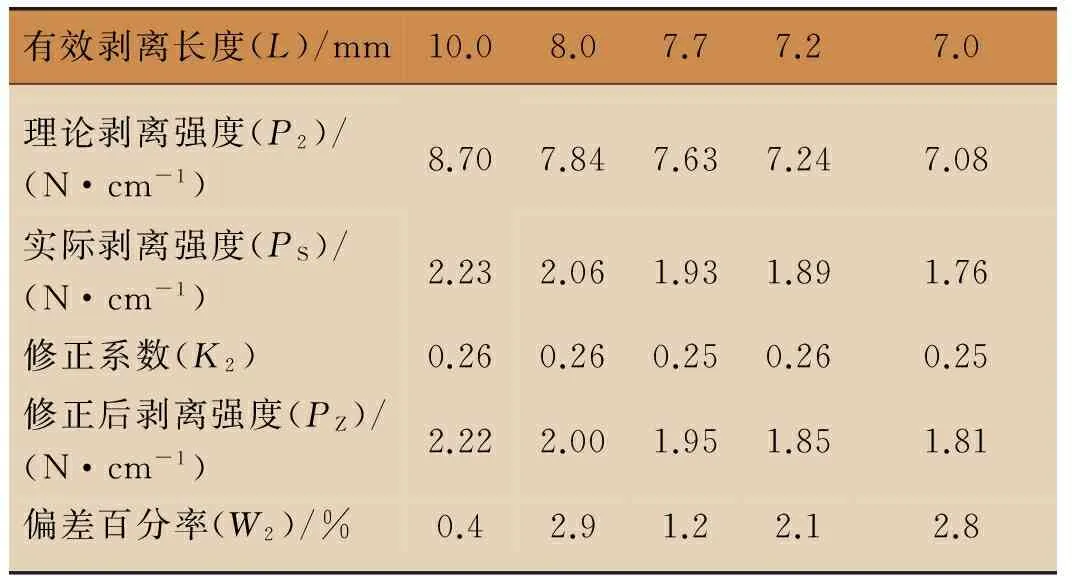
表3　數據綜合表

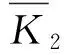
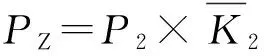
代入式(2)、式(3)及式(7)，則此類自黏運動繃帶的剝離強度計算式為

PZ=-0.474L3+8.913L2-33.89L+5.624

(8)

由表3可見，二次修正后剝離強度偏差百分率W2小于3%，因此式(8)可用于計算和預測該類自黏運動繃帶的剝離強度[4]。

4　結論

將自黏運動繃帶背部膠層設計為條狀花紋，花紋寬度、間隔固定不變，條狀花紋與寬度方向成一定夾角，基于Maxwell模型建立了自黏運動繃帶剝離強度計算式，經過二次修正，計算得到的剝離強度偏差百分率<3%，因此該計算式可用于計算和預測此類自黏運動繃帶的剝離強度，指導此類系列產品的設計和選用。

[1]張潔，錢曉明.彈性繃帶的發展及其在醫療領域的應用[J].棉紡織技術，2011,39(8):541-544.

[2]于偉東，儲才元．紡織物理[M]．上海：東華大學出版社，2002:79-88.

[3]上海橡膠制品研究所．GB/T 2792—1998壓敏膠黏帶180°剝離強度試驗方法[S]．北京：中國標準出版社，1998.

[4]莊楚強，何春雄.應用數理統計基礎[M].廣州：華南理工大學出版社，2007：32-83．

Research on physical model of peeling strength of self-adhesive sport bandage

Li Yupeng1,Wang Qi1,Liu Changjie2,Guo Chaoqun2,Liu Bo2

1.Key Lab of Textile Science and Technology,Ministry of Education,Donghua University,Shanghai/China 2.Wuxi Paiho Textile Co.,Ltd.,Wuxi/China

The self-adhesive sport bandage was designed with bar pattern adhesive layer.The bar pattern was 2 mm wide according to a separation of 1 mm.The angle were formed between bar pattern and width direction with 0,15,30,45 and 90 degrees.The formula of peeling strength of self-adhesive sport bandage was set up based on Maxwell model.It could be used to calculate and predict peeling strength of this kind of self-adhesive sport bandage.The deviation percentage calculated was less than 3%.

self-adhesive sport bandage; peeling strength; model