改進Terminal滑模永磁直線同步電機控制策略研究*
程 帆, 余海濤, 李忠坤, 徐鳴飛
(東南大學 電氣工程學院,江蘇 南京 210096)
?
改進Terminal滑模永磁直線同步電機控制策略研究*
程帆,余海濤,李忠坤,徐鳴飛
(東南大學 電氣工程學院,江蘇 南京210096)
永磁直線同步電機(PMLSM)作為一種高階非線性系統,需要通過優化的控制算法來實現伺服系統的高精度和快速響應。非線性控制理論對于非線性系統有較好的控制性能,其中Terminal滑模控制相比較于傳統滑模控制,具有收斂精度高的特點,并保留了滑模控制的魯棒性。分析了PMLSM的數學模型,設計了基于非奇異Terminal位置滑模控制和一個一階速度滑模面,通過二者的組合實現速度限幅和位置的精確響應。通過MATLAB/Simulink的仿真,結果表明,該方法下的PMLSM的改進Terminal滑模控制具有較高的控制精度和較快的響應速度,在存在外部擾動的情況下也具有較好的魯棒性。
永磁直線同步電機; 磁場定向控制; 矢量控制; 非奇異Terminal滑模控制
0 引 言
以無鐵心永磁直線同步電機(Permanent Magnet Linear Synchronous Motor, PMLSM)為代表的直驅型伺服系統,相比較傳統的滾珠絲杠式間接驅動,具有精度高、響應快、結構簡單等優勢,是數控機床加工的主要發展方向。為了克服直線電機所存在的端部效應及周期性波動等干擾因素,實現高精度的控制,目前研究主要集中在以兩電平逆變器為基礎,以矢量控制和直接轉矩控制為代表的控制策略的改進上。其中包括了基于μ理論的魯棒重復控制[1]、基于x域重復控制[2]、基于H∞魯棒控制和零相位誤差跟蹤控制器[3]、基于二階滑模的PMLSM調速系統[4]、模糊控制[5]等控制策略,以及基于干擾觀測器的控制結構[6]。其中,滑模控制由于魯棒性好、響應速度較快等特點,在PMLSM控制中得到了廣泛應用。
由于滑模控制存在的抖振問題和傳統滑模面存在收斂精度有限的問題,本文在這些文獻的基礎上,設計了一種改進的Terminal滑模控制策略。結合了Terminal滑模快速響應的特點,并使用輔助速度滑模面實現速度的限幅輸出,簡化了位置-速度環控制器的結構設計。在此基礎上,MATLAB/Simulink的仿真結果表明,在給定位置較小的情況下,Terminal滑模控制器可以實現位置給定的快速響應并有較高的精度;在位置信號給定較大時,通過速度滑模面可以實現速度的限幅輸出。從而證明了該結構滑模控制器可以在實現定位精度和響應速度提高的基礎上,簡化控制器的結構。
1 PMLSM的模型和矢量控制策略
相比較于有鐵心結構或者單邊PMLSM,雙邊無鐵心PMLSM具有力能指標高、體積小及推力波動小等諸多優勢,是直驅型高精度數控機床的主要發展方向[7]。在一般的永磁直線電機d-q軸數學模型中,令永磁體基波勵磁磁場軸線為d軸,q軸為順運動方向超前90°電角度的軸線。在三相繞組完全對稱、磁場沿氣隙正弦分布的前提下,可以得到表貼式(面裝式)永磁直線電機的電壓矢量方程:
(1)
式中:ud、uq——直軸和交軸電壓分量;
Rs——電樞繞組的等效電阻;
Ld、Lq——直軸和交軸電感;
ωe——電角速度值;
Ψf——永磁體在電樞繞組中的磁鏈值;
p——微分算子。
PMLSM電磁推力和機械運動的表達式則為
(2)
式中:Fe——電磁推力;
Kf——電磁推力常數;
iq——q軸電流;
M——PMLSM動子和負載的等效質量;
v——運動速度;
B——粘滯摩擦因數;
F——由于電機參數變化以及外界擾動和非線性摩擦力所造成的擾動量。
2 Terminal滑模改進矢量控制策略
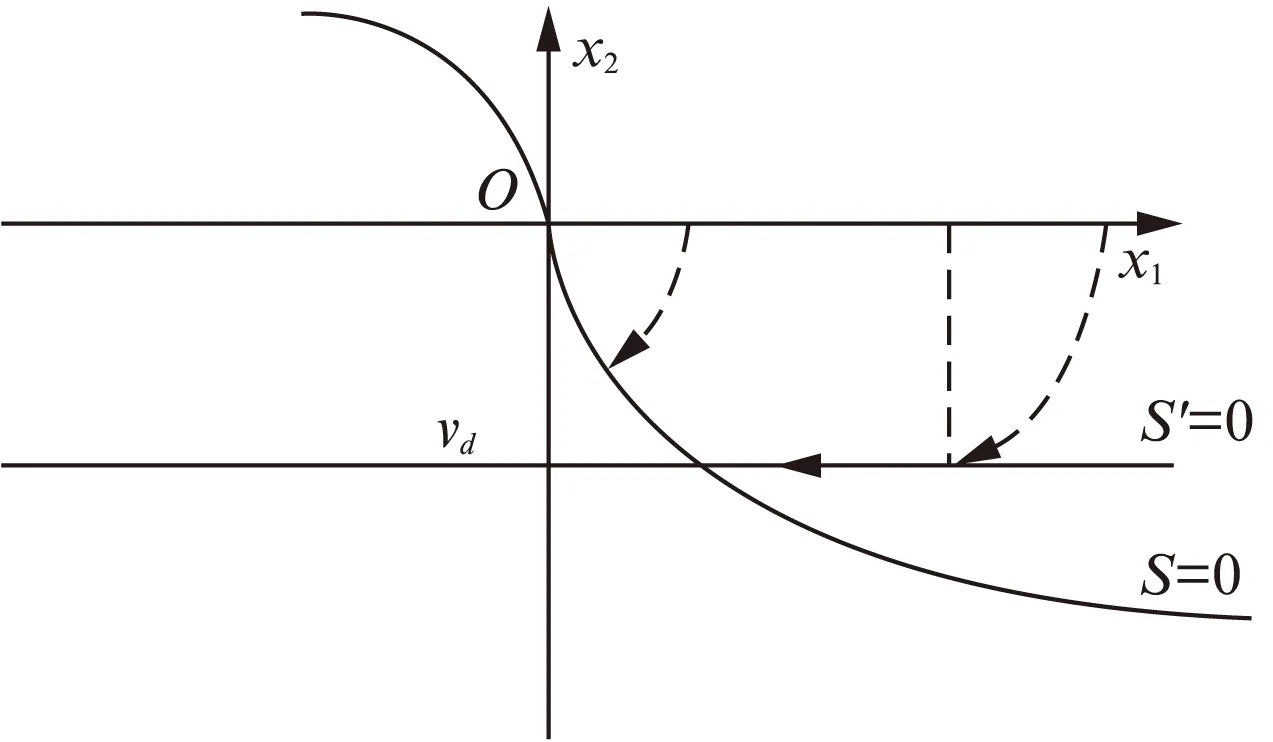
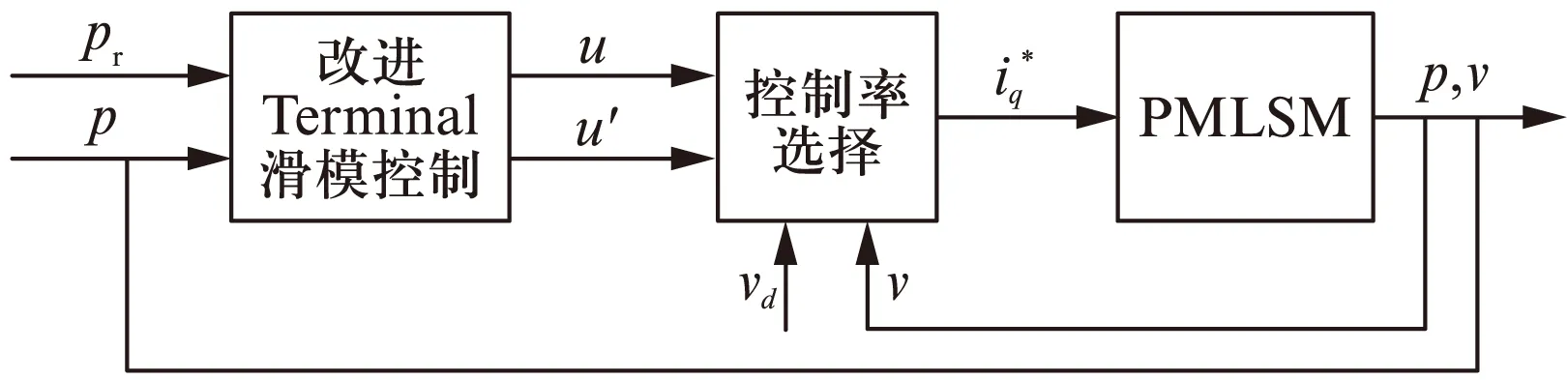
一般的PMLSM的矢量控制策略中,包含位置-速度-電流三閉環。通常在直軸和交軸電流環采用PI控制器,可以獲得較快的響應速度。在位置- 速度控制器設計時,采用了一種基于改進之后的Terminal滑模控制器結構,可以實現動子的精確定位和速度的限幅輸出[8]。具體為采用非奇異Terminal滑模面設計位置滑模控制器,并使用一階滑模面設計輔助的速度滑模控制器,在實現精確定位的基礎上可以實現速度的限幅輸出。
2.1Terminal位置滑模控制器的設計
由PMLSM的電磁推力方程,并設給定位置信號為pr,動子反饋的位置信號為p,位置誤差為x1,x1的一階導數為x2。滿足式(3)所示:
(3)
由電磁推力方程式可得到關系式:
(4)
式中:u——控制量,u=iq。
設計Terminal滑模面S,滿足[9]:
(5)
式中:β>0,p、q滿足1
設計滑模器的輸出u滿足:
(6)
其中:
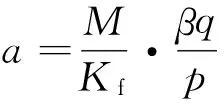
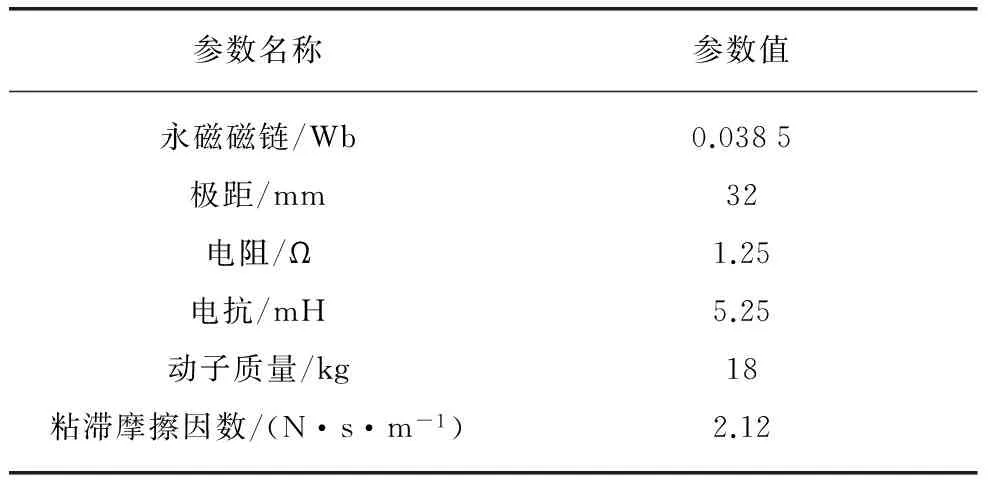
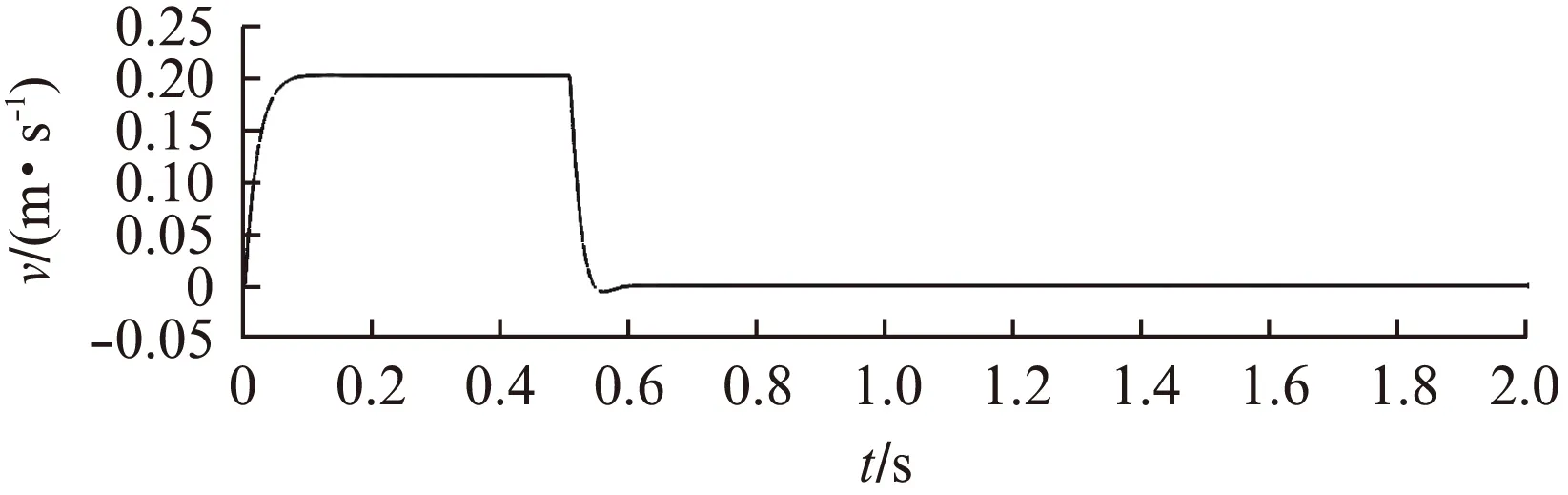
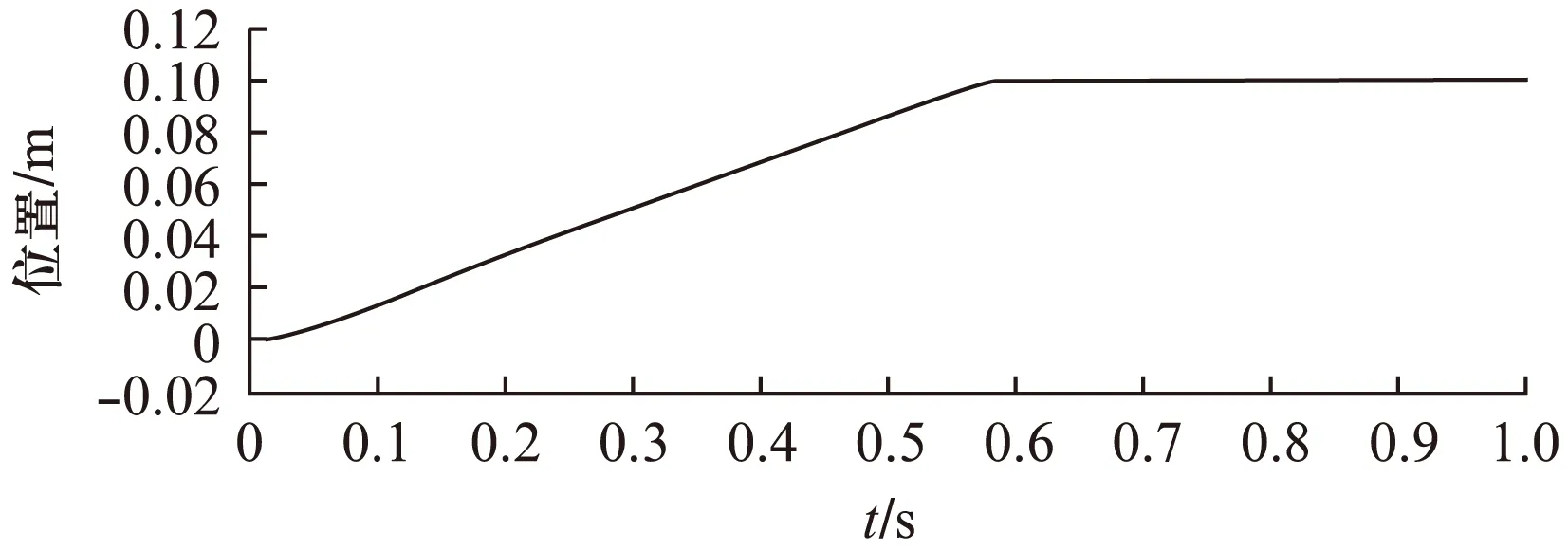
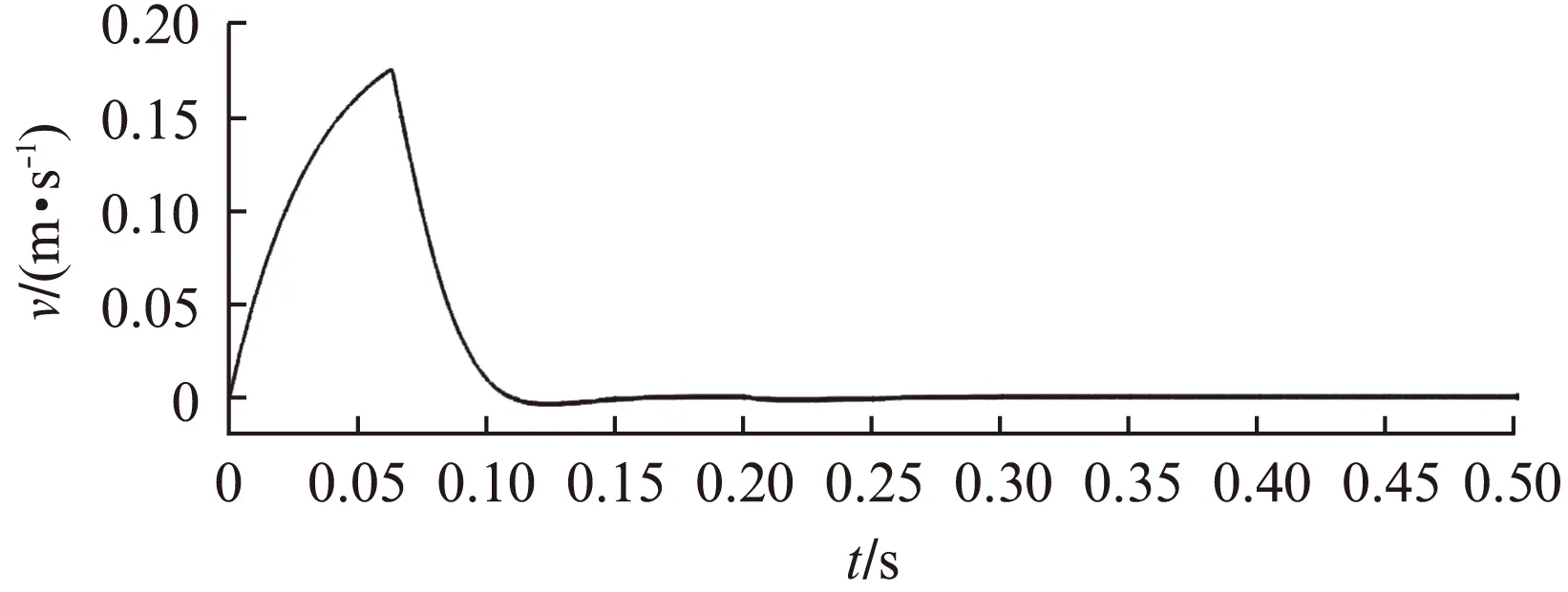
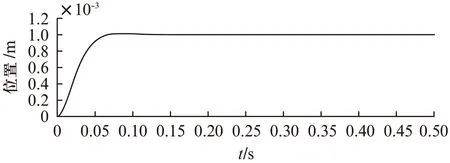
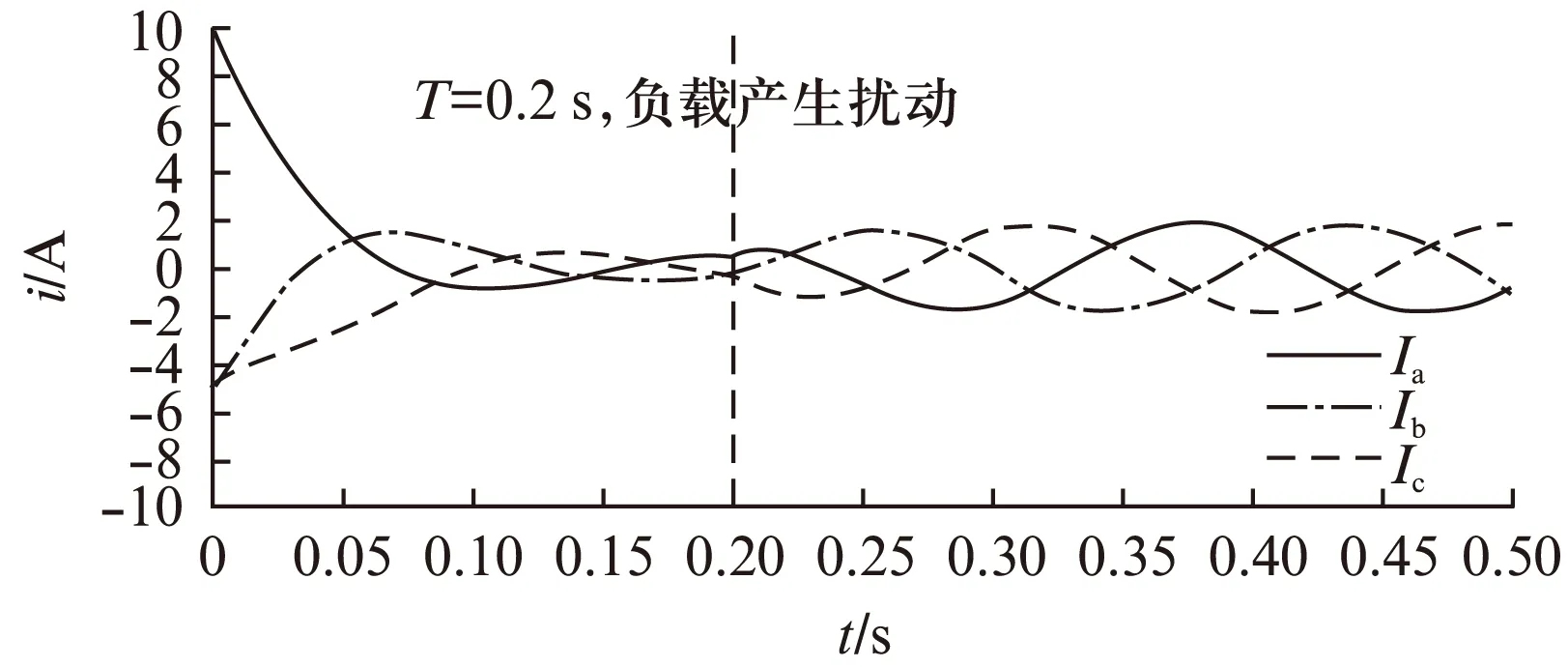
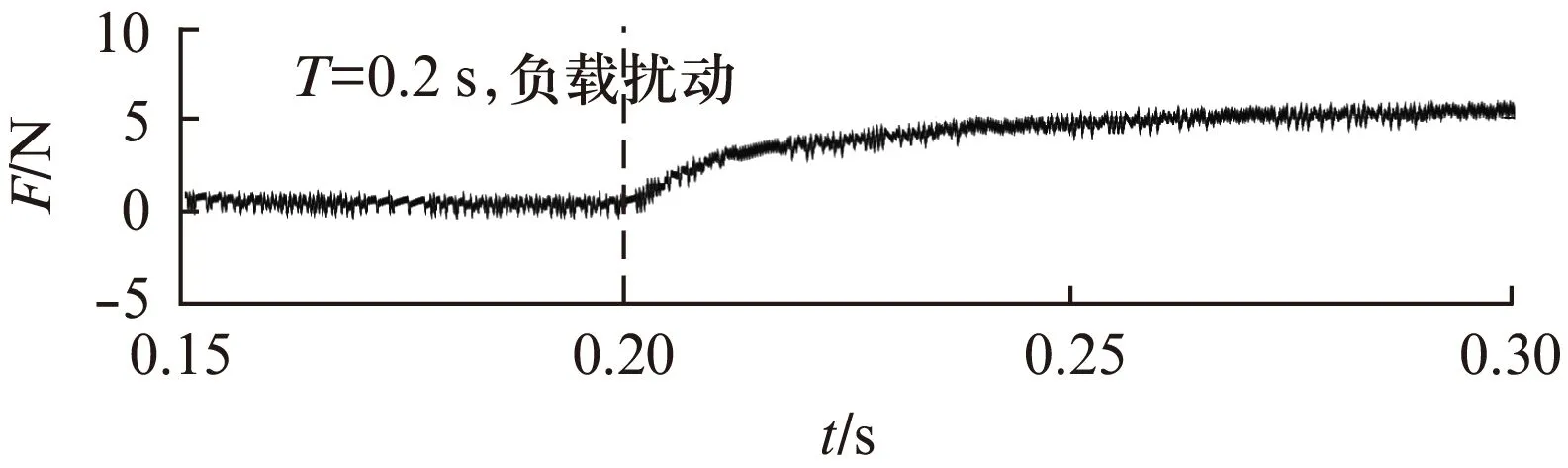
若假設擾動量F滿足關系式|F| k>b|l/M| 那么可以證明該控制率滿足Lyapunov穩定性。 選擇Lyaponov函數: (7) 可以證明Lyapunov穩定性如下: 滿足Lyapunov穩定性條件。 Terminal位置滑模控制器的結構如圖1所示。 圖1 Terminal滑模控制器結構 圖1中,pr為位置輸入給定量,p為位置反饋量。通過引入Terminal滑模位置控制器,即在原系統中引入新的閉環控制。通過選擇合理的滑模面增益和其他參數,使得滑模控制器的輸出滿足Lyapunov穩定性,并在保持魯棒性的基礎上實現較短時間內收斂。 2.2輔助速度滑模控制器的設計 速度滑模面S′設計為 (8) 其中:vd=-vmax,vmax為動子的速度限制幅值。 由此可得到速度滑模的控制率: u′=φ3+φ4x2 (9) 可以證明Lyapunov穩定性如下: 滿足Lyapunov穩定性條件。 2.3位置伺服系統的設計 選定速度滑模面和位置滑模面后,可分析系統的運行相軌跡,分為兩種情況進行討論。不同情況下的運行相軌跡如圖2所示。 圖2 系統運行相軌跡 當參考位置較小時,系統可直接到達位置滑模階段,沿著位置滑模面S運動到原點達到穩定;當相對參考位置較大時,系統由初始狀態首先到達速度滑模階段,沿著速度滑模面S′運動到S和S′交點之后,再沿著位置滑模面S運動到原點達到穩定。 如圖2所示,在系統起動加速階段使用電流內環進行限幅,實現快速平穩起動。當經過起動加速,電機速度達到速度限幅值vmax時,系統進入速度滑模控制階段(相對參考位置較小時不經歷該階段),保證電機按vmax平穩運行。當系統運行至速度滑模面S′=0和位置滑模面S=0的交點時,進入位置滑模控制階段,在該階段系統沿位置滑模面S=0做滑模運動。 當初始狀態不在位置滑模面S上時,設tr為到達滑模面S的時間。當到達位置滑模面,即滿足條件: 可以解得從初始狀態到最終狀態x1(ts)=0的時間[10]: 證明當運動到位置滑模面之后,在有限時間內可以達到收斂,從而相比一般的滑模控制具有更高的控制精度。采用的改進Terminal滑模控制器的總體結構如圖3所示。 圖3 改進Terminal滑模控制器結構圖 仿真PMLSM采用無鐵心結構,詳細參數如表1所示。 表1 無鐵心直線電機的參數 根據表1中的電機參數,在MATLAB/Simulink中構建整個控制系統的模型進行仿真。分以下三種情況進行驗證。 (1) 情況1: 在位置給定為0.1m、速度限幅值vmax給定為0.2m/s情況下,位置給定,速度響應和位置響應結果如圖4、圖5所示。 圖4 情況1下速度響應曲線 圖5 情況1下位置響應曲線 (2) 情況2: 在位置給定為0.01m、速度限幅值vmax給定為0.2m/s情況下,位置給定,速度響應和位置響應結果如圖6、圖7所示。 圖6 情況2下速度響應曲線 圖7 情況2下位置響應曲線 綜合比較上述兩種情況,當位置給定信號較小時(情況2),系統直接由初始速度為0的狀態通過Terminal位置滑模面S運動到給定位置;當位置給定信號較大時(情況1),系統初始速度為0的狀態首先運動至滑模面S′狀態,在該滑模面上實現了v=vmax的速度限幅輸出,在到達S′和S交界點之后,通過Terminal位置滑模面S減速到給定位置收斂。 (3) 情況3: 考慮在位置給定為0.1m、速度限幅值vmax給定為0.2m/s情況下,在T=0.2s時負載出現擾動,三相電流和電磁推力如圖8、圖9所示。 圖8 三相電流波形 圖9 電磁推力波形 從圖8、圖9可看出,在快速起動之后電流波形很快穩定,當外部施加負載擾動之后,電流波形和電磁推力很快趨于穩定,證明了該控制策略具有較好的魯棒性。 本文針對PMLSM伺服系統,結合非奇異Terminal滑模控制,構建了一種新的伺服控制策略。通過非奇異Terminal滑模在有限時間內收斂和一階速度滑模對于速度的限幅輸出作用,可以實現速度的限幅輸出和位置的高精度響應。使用MATLAB/Simulink對該系統進行了不同位置給定信號和存在負載擾動下的仿真。仿真結果證明該方法可以在速度限幅的基礎上,實現控制器結構的簡化,并具有較強的魯棒性。 [1]孫宜標,閆峰,劉春芳.基于μ理論的永磁直線同步電機魯棒重復控制[J].中國電機工程學報,2009,29(30): 52-57. [2]孟高軍,余海濤,黃磊,等.基于x域重復控制的磁通切換永磁直線電機定位力抑制方法[J].中國電機工程學報,2015,35(16): 4224- 4231. [3]曲永印,趙希梅,郭慶鼎.基于零相位誤差跟蹤控制器的輪廓誤差交叉耦合控制[J].中國機械工程,2006,17(11): 1135-1137. [4]陸華才,徐月同,楊偉民,等.永磁直線同步電機進給系統模糊PID控制[J].電工技術學報,2007,22(4): 59-63. [5]孫宜標,楊雪,夏加寬.基于二階滑模的永磁直線同步電機的魯棒速度控制[J].電工技術學報,2007,22(10): 35- 41. [6]李志軍,劉成穎,孟凡偉,等.基于ZPETC和DOB的直線電機控制器設計及實驗研究[J].中國電機工程學報,2012,32(24): 134-140. [7]王昊,張之敬,劉成穎.永磁直線同步電機縱向端部效應補償方法[J].中國電機工程學報,2010,30(36): 46-52. [8]姜長生,吳慶憲,費樹岷.現代非線性系統魯棒控制基礎[M].哈爾濱: 哈爾濱工業大學出版社,2012. [9]張前,黃學良,周贛.永磁同步直線電動機的位置滑模控制器設計[J].微特電機,2010,38(5): 53-55. [10]LI S, ZHOU M, YU X. Design and implementation of terminal sliding mode control method for PMSM speed regulation system[J]. IEEE Transactions on Industrial Informatics, 2013,9(4): 1879-1891. Research of Improved Terminal Sliding Mode Control of Permanent Magnet Linear Synchronous Motor* CHENGFan,YUHaitao,LIZhongkun,XUMingfei (College of Electrical Engineering, Southeast University, Nanjing 210096, China) Permanent magnet linear synchronous motor(PMLSM) was considered as a high order nonlinear system. Thus, the optimization control algorithm was required to realize the high precision and fast response of servo system. Due to the brilliant performance of nonlinear control theory, terminal sliding mode control was applied with high convergence precision and robustness. On base of mathematical model of PMLSM, non singular terminal position sliding mode control and a first order speed sliding mode surface was designed and combined to achieve speed limit and exact response of location. The MATLAB/Simulink simulation results showed that the method of PMLSM improved Terminal sliding mode control had high control precision, fast response and good robustness in the presence of external disturbances. permanent magnet linear synchronous motor(PMLSM); field-oriented control(FOC); vector control; non singular Terminal sliding mode control 國家自然科學基金項目(41576096) 程帆(1992—),男,碩士研究生,研究方向為直線電機伺服驅動控制。 TM 301.2∶TM 351 A 1673-6540(2016)08- 0031- 05 2016-03-09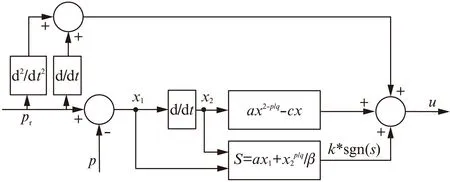
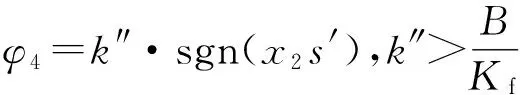
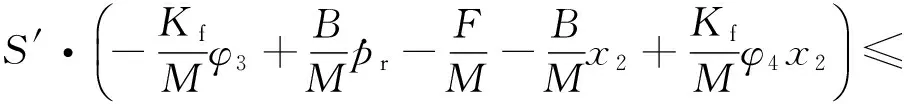
3 仿真及結果
4 結 語

