自導向轉向架曲線運行軸間抗剪系統受力研究*

梁駿宇， 周張義， 楊　欣， 黃運華

(西南交通大學　機械工程學院， 四川成都 610031)

?

自導向轉向架曲線運行軸間抗剪系統受力研究*

梁駿宇， 周張義， 楊欣， 黃運華

(西南交通大學機械工程學院， 四川成都 610031)

為顯著提升曲線通過性能，自導向轉向架采用低軸箱縱向定位剛度和大錐度踏面輪對成為必然，從而需要額外附加軸間抗剪系統以確保足夠的直線蛇行穩定性。首先，基于線性穩態解析并以最佳曲線通過為目標，論述了Scheffel提出的軸箱縱向定位剛度匹配設計原理；其次，進行非線性動態曲線通過數值仿真，驗證了參數匹配條件下軸間抗剪系統處于不承載的理想工作狀態；最后，組合不同軸箱縱向定位剛度和軸間抗剪系統剪切剛度參數取值，仿真分析了參數不匹配條件下軸間抗剪系統的受力變化規律，提出自導向轉向架要實現最佳曲線通過，則必須采用匹配設計的軸箱縱向定位剛度，此時軸間抗剪系統僅在直線運行時承受較大載荷；若轉向架其他運行性能要求采用更大的軸箱縱向定位剛度，則為確保曲線通過較大程度接近最佳性能，實際應用的參數應取匹配值的2～4倍為宜，軸間抗剪系統的剪切剛度盡量取低值，此時其在曲線運行時承受較小載荷。

自導向轉向架； 曲線通過； 軸間抗剪系統； 受力分析； 剪切剛度； 軸箱縱向定位剛度

車輛通過曲線時，輪對不出現輪緣貼靠鋼軌，并最大程度沿徑向純滾線運動，從而顯著降低輪軌磨耗，是自導向轉向架的設計目標。為此，采用大錐度踏面輪對和低軸箱縱向定位剛度成為必然。由于這將同時導致直線蛇行穩定性大幅降低，因此自導向轉向架需額外設置軸間抗剪系統。其根本作用是提供轉向架主要的剪切剛度，確保足夠的直線蛇行穩定性，同時不影響柔軟軸箱縱向定位形成的轉向架低彎曲剛度，確保高曲線通過性能。圖1為3種典型軸間抗剪系統示意圖。

理論上，根據蠕滑力導向機理，軸間抗剪系統并不能被認為是一種導向裝置。轉向架自導向完全是依靠具有足夠車輪踏面錐度的低搖頭約束輪對，在曲線上依靠輪軌蠕滑力自動調整至徑向純滾位置實現的。軸間抗剪系統應根據不妨礙輪對曲線自導向能力原則設計，其在轉向架中僅僅起穩定直線蛇行運動的作用。基于此，軸間抗剪掛系統在轉向架曲線運行中并不承受很大

載荷，理想工作模式是處于不承載的自由釋放狀態，從而其剪切剛度不影響輪對自導向能力，此時轉向架可實現最佳曲線通過。

以往研究中，以最佳曲線通過為目標，就自導向轉向架關鍵參數匹配設計研究基本來自于Scheffel[1-4]，核心為輪對軸箱縱向定位剛度與其重力剛度間的參數匹配。而更多偏向工程化的應用研究[5-7]，通常僅強調相對于常規轉向架，自導向轉向架應采用較低軸箱縱向定位剛度的必要性，但基本未涉及實現最佳曲線通過所需相關參數間的潛在匹配問題。實際應用中的參數取值設計仍基于常規折中法，即在滿足車輛各項運行性能指標基礎上，選取較低軸箱縱向定位剛度。

可見，上述兩種不同的參數設計方法，勢必導致自導向轉向架曲線運行時軸間抗剪系統處于不同的受力狀態。由于前者采用匹配設計的參數，著重強調實現最佳曲線通過，因此其軸間抗剪系統通常受力很小，接近處于不妨礙輪對曲線自導向的理想工作狀態；而后者并不進行嚴格的參數匹配，著重折中考慮各類運行性能，無法達到最佳曲線通過，故其軸間抗剪系統通常受力不小，輪對自導向能力將受到一定影響。

考慮到軸間抗剪系統受力狀態，不僅影響自導向轉向架曲線通過性能，而且直接關系其結構自身強度可靠性設計。鑒于此，針對Scheffel提出的參數匹配設計原理進行必要論述基礎上，著重應用多體動力學數值仿真技術，系統分析關鍵懸掛參數不同組合條件下，自導向轉向架曲線運行時軸間抗剪系統的受力狀態及變化規律，為工程應用中更為合理的參數設計提供理論依據。

1　軸箱縱向定位剛度匹配設計

在足夠輪軌間隙前提下，車輪踏面具有錐度的自由輪對具備沿曲線徑向純滾動的能力，即輪對軸線在徑向線上和輪對中心在純滾線上。當輪對偏離該穩態位置時，借助輪軌間相應產生的蠕滑力，輪對將圍繞徑向純滾線持續進行回調運動，完成曲線導向運行。

可見，輪對需要滿足零搖頭約束和純滾線位于輪軌間隙之內兩個條件，才能達到理想曲線通過。考慮實際有限的輪軌間隙，如我國LM型踏面輪對與60 kg/m鋼軌匹配時的輪軌間隙約為9 mm，必須采用大錐度踏面輪對，方能使自導向轉向架通過小半徑曲線時不出現輪緣貼靠鋼軌。

對于大錐度踏面輪對，由于其發生橫移運動后存在顯著的重力剛度Kws，相應產生的橫向重力復原力Kws對輪對受力平衡產生較大影響，因此在輪對曲線通過受力分析中不能忽略。在該情形下，對于兩軸間彎曲剛度為零的輪對，因橫向受力不平衡其曲線通過的理想穩態位置將無法達到徑向線，如圖2(a)所示。前后輪對必須同時逆時針旋轉一定搖頭角而產生輪軌橫向蠕滑力，以平衡非零重力剛度引起的橫向重力復原力，達到實際穩態平衡位置，如圖2(b)所示。此時輪對仍可達到純滾線位置，即輪軌間僅有橫向蠕滑而無縱向蠕滑。圖2中，r0為車輪名義滾動圓半徑，λ為車輪踏面等效錐度，2a為轉向架軸距，2l為同一輪對輪軌接觸點橫向跨距，2θ為軸間徑向夾角，y0為輪對純滾橫移量，R為線路曲線半徑，Kx為軸箱縱向定位剛度。

進一步，如果軸間彎曲剛度不為零，即存在一定軸箱縱向定位剛度，則由于定位彈簧變形承載而影響輪對受力平衡，導致理想純滾線也無法達到。如圖2(c)所示，為使得輪對在橫向、縱向及回轉方向均達到受力平衡，一方面前后輪對需要相對純滾線分別向外和向內橫移，以便產生作用方向相反的縱向蠕滑力矩來平衡定位彈簧復原力矩，達到輪對在縱向和回轉方向的受力平衡；另一方面，前后輪對還需分別逆時針和順時針反相搖頭，以便使前后輪對橫向蠕滑力發生增減，適應因輪對相對純滾線橫移而產生的橫向重力復原力增減，達到輪對在橫向的受力平衡。

上述分析表明，當采用大錐度踏面輪對后，與軸箱縱向定位剛度一樣，重力剛度也成為影響曲線通過不可忽略的負面因素，且二者間存在耦合作用影響。雖然零彎曲剛度是保證轉向架理想曲線通過的前提，但其也將導致表征蛇行運動失穩的臨界速度為零，實際中不可能采用。實際上，對于采用大錐度踏面輪對的自導向轉向架，一定的軸箱縱向定位剛度還將有利于降低重力剛度對曲線通過的不利影響。當二者參數間達到特定匹配關系時，不利影響將降至最低，軸間抗剪系統可處于不承載的自由釋放狀態，達到其剪切剛度僅決定直線蛇行穩定性，而不影響曲線通過性能的理想工作模式。

對于采用大錐度踏面輪對、軸間存在一定彎曲剛度且附加軸間抗剪系統的二軸自導向轉向架，同樣由于受力不平衡輪對無法達到理想曲線通過的徑向純滾位置，如圖3(a)所示。類似圖2，經過整體回轉和輪對間反相搖頭運動的疊加，轉向架可達到實際的最終受力平衡穩態位置。

圖2　大錐度踏面輪對曲線穩態位置分析

圖3　自導向轉向架輪對曲線穩態位置分析

首先，轉向架系統可整體繞其垂向中心軸逆時針回轉角φ，如圖3(b)所示(圖中f11和f22分別為輪軌縱向和橫向蠕滑系數)，前后輪對由此產生平衡橫向重力復原力的橫向蠕滑力，即：

(1)

其中：Kws為重力剛度。

因此，滿足上式所需的整體回轉角為：

(2)

相應地，該整體回轉角引起的前后輪對相對純滾線向外和向內的橫移量為ΔY=aφ，從而導致其各自橫向重力復原力的增減量為：

(3)

可見，此時每個輪對的橫向蠕滑力和橫向重力復原力不平衡。對于前輪對，橫向蠕滑力小于橫向重力復原力，而后輪對則剛好相反，每個輪對的橫向不平衡力即為ΔF。要使其各自達到最終的橫向受力平衡，則軸間徑向夾角2θ需減小2φ，即前后輪對分別逆時針和順時針產生反相搖頭角φ，如圖3(c)所示，使各自輪軌橫向蠕滑力分別增減達到2f22φ=ΔF。因此，輪對橫向平衡所需的搖頭角φ為：

(4)

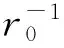
(5)

將式(2)和式(4)代入式(5)并整理可得：

(6)

上述分析表明，若輪對軸箱縱向定位剛度與其重力剛度達到式(6)所表達的匹配關系，則通過該縱向定位彈簧的耦合作用，前后輪對將在縱向及回轉方向也達到受力平衡。此外還可得知，由于整體回轉角φ和反相搖頭角φ兩種調節運動，均不會引起軸間抗剪系統承受載荷作用，因此輪對在水平方向內的力及力矩平衡與其剪切剛度取值無關。

以上即是Scheffel基于線性轉向架系統的穩態曲線通過分析，提出的自導向轉向架軸箱縱向定位剛度的匹配設計基本原理。若再假設輪軌縱向和橫向蠕滑系數也相等，并忽略角φ(小半徑曲線上該值通常很小)的影響，則式(6)可進一步簡化為：

(7)

可見，就確定的線路和轉向架總體幾何參數，輪對軸箱縱向定位剛度與其重力剛度間存在單調線性關系。基于該參數設計方程，自導向轉向架可實現略微偏離理想徑向純滾位置的最佳曲線通過。

2　參數匹配下軸間抗剪系統受力驗證

如上論述，當輪對軸箱縱向定位剛度與其重力剛度達到匹配設計時，自導向轉向架最佳曲線通過得以實現，軸間抗剪系統將處于不承載的自由釋放狀態，其剪切剛度對曲線通過性能無影響。考慮到該結論是在諸多前提假設下進行線性穩態解析得到的，如輪軌接觸、蠕滑和彈性元件均呈線性特性，各向蠕滑系數相等及未考慮自旋蠕滑等。因此有必要在考慮各種實際因素條件下，對軸間抗剪系統的受力進行驗證。

應用SIMPACK多體動力學仿真軟件，考慮輪軌接觸幾何非線性、各向蠕滑非線性、自旋蠕滑等實際因素，基于我國LM型踏面輪對與60 kg/m鋼軌匹配，建立了準軌25 t軸重3大件自導向轉向架的動態曲線通過仿真模型。其中，軸間抗剪系統采用圖1(a)所示方案，每個副構架首先將同一輪對左右軸箱相連，然后通過兩交叉桿進行鉸接，兩交叉桿承受的軸向拉壓載荷即可體現整個軸間抗剪系統的受力狀態。

首先，通過變參數分析，分別仿真確定轉向架在曲線半徑線路300～600 m上，以均衡速度運行達到最佳曲線通過所需的軸箱縱向定位剛度值。根據線性解析推導,最佳曲線通過的實現標準為軸間抗剪系統處于基本不承載的自由釋放狀態，即交叉桿載荷最小，仿真中取其目標載荷值小于0.1 kN。表1所列為仿真和按式(7)解析確定的軸箱縱向定位剛度匹配值結果對比。可見，二者存在一定差異，仿真結果要小于解析結果，即要達到最佳曲線通過實際中需要更小的軸箱縱向定位剛度。若解析推導中盡可能減少簡化和假設，則解析結果將接近仿真結果。

表1　軸箱縱向定位剛度解析和仿真匹配結果對比

從表1還可看出，一方面自導向轉向架所需最優軸箱縱向定位剛度較常規轉向架要小的多，通常至少要小一個數量級，如南非Scheffel轉向架采用的定位剛度最小達0.3 MN/m；另一方面，由于隨線路曲線半徑減小，輪對純滾所需橫移量增大，重力剛度也相應增大，從而匹配確定的定位剛度呈增大趨勢。

圖4所示為轉向架以均衡速度運行至圓曲線上，輪對穩態橫移和沖角(相對于徑向線的搖頭角)仿真與解析結果對比，圖中同時給出了純滾橫移量和軸箱縱向定位剛度很大的剛性轉向架輪對沖角(a/R)。可見，一方面仿真與解析結果不僅差異很小，而且分布規律也相同，即前后輪對相對純滾線分別向外和向內橫移，相對徑向線均搖頭呈欠導向狀態，且前輪對沖角略大于后輪對；另一方面，通過與純滾橫移量和剛性轉向架輪對沖角對比可知，前后輪對處于略微偏離理想徑向純滾線的位置，驗證了通過匹配設計軸箱縱向定位剛度，可使自導向轉向架達到最佳曲線通過。

圖4　輪對穩態橫移和沖角的解析與仿真結果對比

表2列出了軸間抗剪系統剪切剛度Ks取不同值，轉向架通過300 m和600 m半徑曲線時，輪對穩態橫移和沖角仿真結果對比。可見，當采用匹配設計的軸箱縱向定位剛度后，Ks取值將不影響輪對的曲線通過穩態運動位置。圖5所示為轉向架通過300 m半徑曲線時，Ks分別取3，6，12，24 MN/m，交叉桿載荷時間歷程仿真結果對比。可見，在圓曲線上交叉桿穩態載荷幾乎為零，且與Ks無關，軸間抗剪系統處于基本不承載的理想工作狀態；在緩和曲線上，由于線路曲率和超高不斷變化，導致參數間匹配關系暫時喪失，從而交叉桿將瞬態承載，且其載荷隨Ks增大而增大，與文后給出的參數不匹配條件下交叉桿載荷變化規律類似。其中，交叉桿1延長線指向前輪對外側軸箱和后輪對內側軸箱，交叉桿2與之相反。

表2　不同Ks下輪對穩態橫移和沖角仿真結果對比

圖5　不同Ks下交叉桿載荷仿真結果對比

圖6所示為轉向架以均衡速度通過300 m半徑曲線時，有無軸間抗剪系統下輪對橫移和沖角時間歷程仿真結果對比。可見，兩種情形下輪對在圓曲線上的穩態運動時間歷程幾乎一致，不受Ks影響；在緩和曲線上，同樣由于參數匹配關系的暫時喪失，從而軸間抗剪系統的存在將導致輪對運動，尤其是搖頭運動較無軸間抗剪系統轉向架輪對發生變化，一定程度上說明軸間抗剪系統不僅影響導向裝置，而且在參數不匹配條件下還將影響輪對的自導向能力。

圖6　有無軸間抗剪系統的輪對橫移和沖角時間歷程仿真結果對比

3　不同參數組合下軸間抗剪系統受力分析

根據表1所列仿真結果，若就最小曲線半徑為300 m 的線路進行最佳曲線通過優化，則可以匹配得到我國25 t軸重自導向轉向架軸箱縱向定位剛度約為0.5 MN/m。可見，該定位剛度較常規轉向架要小得多。若對轉向架要求較高直線蛇行穩定性或定位彈簧同時要傳遞很大的縱向載荷，則該參數取值較難在工程中應用，實際中選取更大的軸箱縱向定位剛度參數成為必然。在此情形下，決定最佳曲線通過的參數匹配關系在圓曲線上也將失去，軸間抗剪系統必然穩態承載，其剪切剛度不僅決定直線蛇行穩定性，而且影響曲線通過性能。

分別取Kx為1，1.5，2，3，5 MN/m，Ks為3，6，12，24 MN/m，對這些參數依次組合進行自導向轉向架動態曲線進行仿真分析。圖7所示為轉向架通過300 m和600 m半徑曲線時，交叉桿1穩態載荷仿真結果對比。交叉桿1和交叉桿2的穩態載荷大小幾乎相等，但作用方向相反，二者分別承受軸向拉伸和壓縮載荷，

圖7　不同Kx和Ks參數組合下交叉桿1穩態載荷仿真結果對比

從圖7及數據對比分析表明，Kx和Ks組合一定時，交叉桿穩態載荷將基本隨轉向架通過的曲線半徑增大而減小；當Kx一定時，交叉桿穩態載荷將隨Ks增大而增大；Ks一定時，交叉桿穩態載荷也將隨Kx增大而增大。在緩和曲線上，交叉桿瞬態載荷在不同Kx和Ks組合下具有相同的變化規律，如圖8所示轉向架通過300 m半徑曲線時，交叉桿載荷時間歷程仿真結果對比。

相應地，圖9和圖10所示為轉向架通過300 m半徑曲線時，不同Kx和Ks組合下輪對橫移及沖角時間歷程仿真結果對比。針對結果的系統分析及對比表明，當Kx一定，隨Ks增大前后輪對均將逐漸橫向外移，前輪對穩態位置偏離純滾線的程度大于后輪對。在Kx取值較小時，上述橫向外移和偏離純滾線程度均很小，如圖9(a)所示。在Kx取值較大時，相應的橫向外移和偏離純滾線程度均很大，如圖9(b)所示。可見，盡可能采用接近匹配值(0.5 MN/m)的低軸箱縱向定位剛度，不僅能有效降低輪對偏離純滾線的程度，而且使其對軸

圖8　不同Kx和Ks參數組合下交叉桿載荷時間歷程仿真結果對比

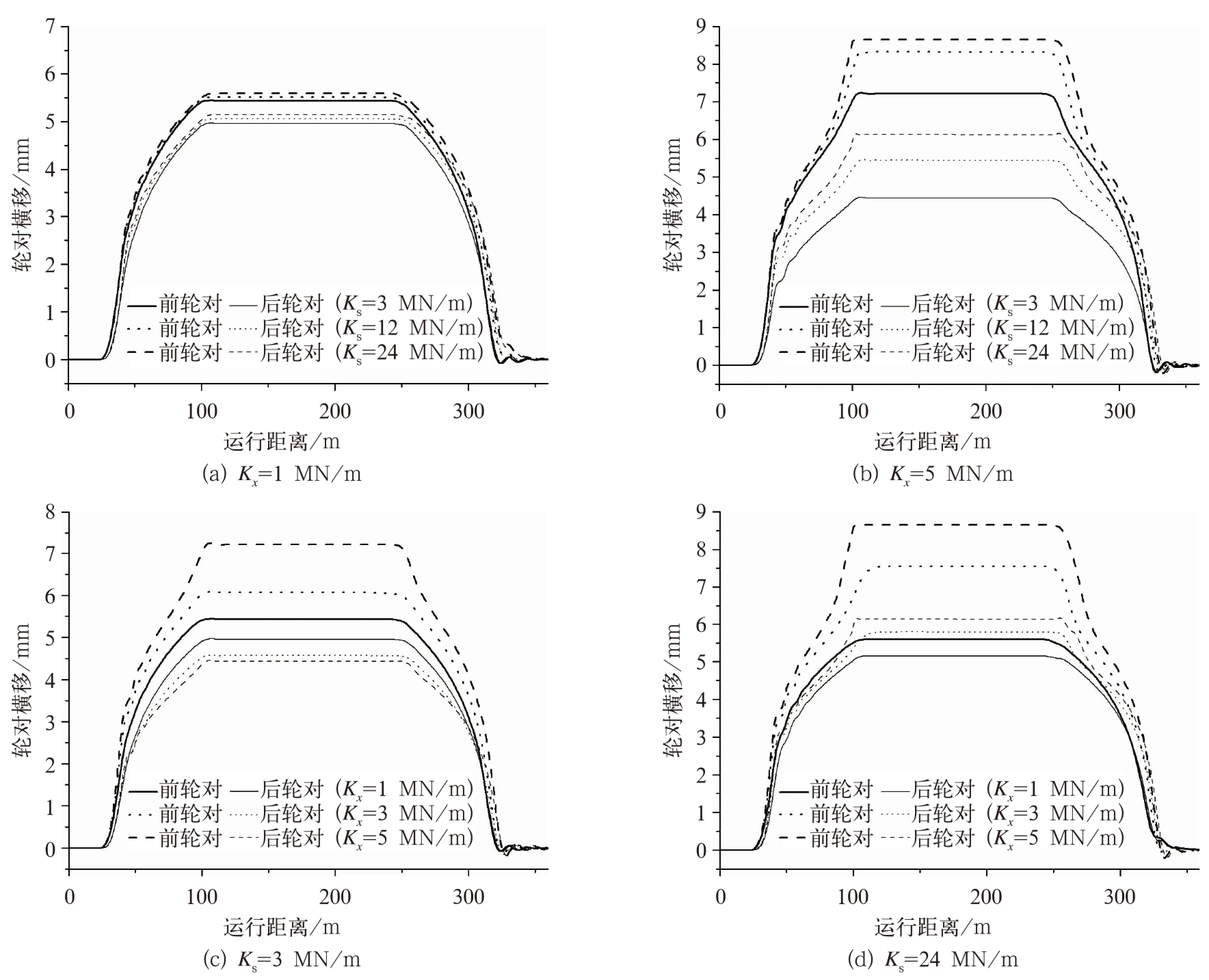
圖9　不同Kx和Ks參數組合下輪對橫移時間歷程仿真結果對比

圖10　不同Kx和Ks參數組合下輪對沖角時間歷程仿真結果對比

間抗剪系統剪切剛度不敏感。

當Ks一定且取值較小時，隨Kx增大前后輪對將分別逐漸橫向外移和內移，如圖9(c)所示。當Ks一定且取值較大時，隨Kx增大前后輪對均將逐漸橫向外移，如圖9(d)所示。兩種情形下，前輪對穩態位置偏離純滾線的程度均大于后輪對。

當Kx一定且取值較小時，隨Ks增大前后輪對將反相搖頭，前輪對始終呈欠導向且沖角逐漸增大，后輪對初始呈欠導向且沖角逐漸較小，隨后呈過導向且沖角逐漸增大，如圖10(a)所示，當Kx一定取值較大時，隨Ks增大前后輪對也將反相搖頭，前輪對穩態位置始終呈欠導向且沖角逐漸增大，后輪對穩態位置則始終呈過導向且沖角也逐漸增大，如圖10(b)所示。兩種情形下，前輪對穩態位置偏離徑向線的程度均大于后輪對。此外同上所述，盡可能采用接近匹配值的低軸箱縱向定位剛度，不僅能有效降低輪對偏離徑向線的程度，而且也可使因軸間抗剪系統剪切剛度增大而引起輪對沖角變化的程度最小。

當Ks一定時，輪對沖角隨Kx增大而發生的變化也有同上基本類似的規律。

進一步對比上述交叉桿載荷與輪對運動位置的變化規律可知，自導向轉向架曲線運行時，軸間抗剪系統的承載大小與輪對偏離最佳曲線通過運動位置的程度直接相關。軸間抗剪系統承載越大，則輪對偏離最佳曲線通過運動位置程度越大，從而輪軌間蠕滑也越大，使得輪對出現滑行的可能性也越大，最終導致轉向架曲線通過性能惡化。因此，通過合理優化參數，盡可能降低軸間抗剪系統受力，不僅可使自導向轉向架接近潛在的最佳曲線通過，而且利于軸間抗剪系統自身結構的強度可靠性設計和運用。

4　工程應用建議

綜上分析，自導向轉向架要實現最佳曲線通過，則必須采用匹配設計的軸箱縱向定位剛度，此時軸間抗剪系統在圓曲線上可實現不承載的理想工作狀態，同時要確保其在緩和曲線上受力也較小，則應盡量采用低值剪切剛度參數。

當轉向架其他運行性能要求采用較匹配值更大的軸箱縱向定位剛度時，為確保曲線通過較大程度接近最佳性能，同時使軸間抗剪系統承載較小，則軸箱縱向定位剛度及軸間抗剪系統剪切剛度兩參數的取值均不宜過大，尤其是軸箱縱向定位剛度。

表3列出了轉向架通過300 m半徑曲線時，Kx分別取0.5,1,2,4 MN/m，Ks分別取3,6,12 MN/m，在兩種參數各種組合條件下，轉向架在圓曲線上各輪對的輪軌穩態蠕滑力仿真結果對比。

表3　不同Kx和Ks參數組合下輪軌穩態蠕滑力仿真結果對比　kN

對比表3數據可見，一方面除后輪對外側車輪外，轉向架其他車輪合成蠕滑力都將隨Kx和Ks增大而增大，轉向架總體曲線通過性能將降低；另一方面，Kx對輪軌蠕滑力的影響程度顯著高于Ks。如當Ks為6 MN/m，Kx分別取匹配值(0.5 MN/m)的2倍(1 MN/m)、4倍(2 MN/m)和8倍(4 MN/m)時，前輪對外側車輪的合成蠕滑力將分別增大9.3%、25.1%和84.6%。當Kx增至4 MN/m時，合成蠕滑力將超過36 kN，十分接近輪軌間最大靜摩擦力(取輪軌摩擦系數為0.3)，很可能首先出現滑行而顯著增大輪軌磨耗。

綜上分析，為盡可能降低增大軸箱縱向定位剛度對曲線通過的不利影響程度，工程應用中其參數取值不宜超過匹配值的4倍，以2倍左右為最佳。在此條件下，采用低值軸間抗剪系統剪切剛度，將有利于進一步提高曲線通過性能。理論分析表明，對于我國25t軸重自導向轉向架，1 MN/m的軸箱縱向定位剛度和5 MN/m的軸間抗剪系統剪切剛度參數組合取值，已可以完全滿足車輛120 km/h的最高速度和其他運行性能指標要求，同時曲線通過仍能很大程度接近潛在的最佳性能。

5　結　論

(1) 論述了Scheffel提出的自導向轉向架輪對軸箱縱向定位剛度的匹配設計原理。當其達到特定匹配值時轉向架可實現最佳圓曲線通過，軸間抗剪系統將處于不承載的理想工作狀態，其對輪對自導向能力的不利影響將得到有效控制；

(2) 基于非線性動態曲線通過數值仿真分析，驗證了參數匹配條件下自導向轉向架可實現最佳曲線通過，軸間抗剪系統的存在并不是作為導向裝置而發揮導向作用，而應僅將其視為穩定轉向架直線蛇行運動的軸間耦合裝置；

(3) 仿真分析了參數不匹配條件下，軸間抗剪系統受力及輪對運動狀態的變化規律。結果表明，軸間抗剪系統的承載大小與輪對偏離最佳曲線通過運動位置的程度直接相關。通過合理優化參數，盡可能降低軸間抗剪系統受力，不僅可使自導向轉向架接近最佳曲線通過，而且利于軸間抗剪系統自身結構的強度可靠性設計和運用。

(4) 自導向轉向架要實現圓曲線上的最佳曲線通過，則必須采用匹配設計的軸箱縱向定位剛度，同時要確保緩和曲線上的良好通過性能，軸間抗剪系統的剪切剛度也應盡量低；

(5) 若轉向架其他運行性能要求采用更大的軸箱縱向定位剛度，則為確保曲線通過較大程度接近最佳性能，實際采用的參數應取匹配值的2～4倍為宜，軸間抗剪系統剪切剛度也應盡量取低值。

[1]H．Scheffel．The Hunting Stability and cCurving Ability of Railway Vehicles[J]．Rail International，1974，(2)：154-176．

[2]H．Scheffel，H M．Tournay．An Analysis of Steady State Deviations of Wheelsets from the Pure Rolling Position Caused by Curved Track and Bogie Inaccuracies[J]．Vehicle System Dynamics，1983，12(1-3)：14-18．

[3]H．Scheffel．南非鐵路徑向轉向架的設計[J]．電力牽引快報，1995，(8-9)：8-13．

[4]H．Scheffel．Unconventional Bogie Designs-Their Practical Basis and Historical Background[J]．Vehicle System Dynamics，1995，24(6-7)：497-524．

[5]R Joly．常規轉向架與徑向轉向架的比較[J]．國外鐵道車輛，1989，26(3)：31-37．

[6]飯田浩平，等(日)．交叉桿式自導向轉向架動力學性能分析[J]．國外鐵道車輛，2007，44(6)：22-27．

[7]李亨利，李芾，傅茂海．貨車徑向轉向架原理及其應用[J]．鐵道車輛，2002，40(4)：25-26．

[8]李芾，傅茂海，黃運華．徑向轉向架機理及其動力學特性研究[J]．中國鐵道科學，2002，23(10)：46-51．

Study on Stress of Inter-axel Shear System for Self-steering Bogie While Curving

LIANGJunyu，ZHOUZhangyi，YANGXin，HUANGYunhua

(School of Mechanical Engineering, Southwest Jiaotong University, Chengdu 610031 Sichuan, China)

In order to improve the curving ability remarkably, it is necessary to use low axel-box longitudinal stiffness and wheelsets with high tread conicity for self-steering bogie. Thus the inter-axel shear system is needed to ensure the enough hunting stability on straight lines. First of all, based on linear steady state analysis and aiming at the best curving, the principles of matching design of axel-box longitudinal stiffness proposed by Scheffel were discussed. Next, through the nonlinear dynamic curving numerical simulation, it is verified that the perfect working status that inter-axel shear system bear no loads while using matched parameters can be achieved. Finally, by combining the different parameter values of axel-box longitudinal stiffness and shear stiffness of inter-axel shear system, the loading variations of inter-axel shear system while using unmatched parameters were analyzed. According to the systemic analysis and comparison of results, the matching designed axel-box longitudinal stiffness must be used for self-steering bogie in order to obtain the best curving. At this case, the inter-axel shear system bears large loads only on straight lines. If the bigger axel-box longitudinal stiffness is needed to satisfy the other bogie running performance, it is recommended that its value applied in practice should be two to four times the matched value. The shear stiffness of inter-axel shear system should be low as soon as possible. In such way, the best curving performance can be reached to a large extent, and low forces will be loaded by inter-axel shear system.

self-steering bogie; curving; inter-axel shear system; stress analysis; shear stiffness; axle-box longitudinal stiffness

1008-7842 (2016) 02-0008-08

??)男，碩士研究生(

2015-11-09)

U260.331

Adoi:10.3969/j.issn.1008-7842.2016.02.02

*中央高校基本科研業務費專項基金資助(2682014CX030)