基于洛倫茲函數的變步長凸組合最小均方算法

曾樂雅，許　華，王天睿

（1.空軍工程大學信息與導航學院，陜西　西安 710077；

2.南京師范大學地理科學學院，江蘇　南京 210046）

基于洛倫茲函數的變步長凸組合最小均方算法

曾樂雅1，許華1，王天睿2

（1.空軍工程大學信息與導航學院，陜西西安 710077；

2.南京師范大學地理科學學院，江蘇南京 210046）

為進一步減小收斂速率與穩態誤差之間的矛盾，改善自適應濾波算法，利用改進的Lorentzian函數提出了一種新的變步長凸組合最小均方（new variable step-size convex-combination of least mean square，NVSCLMS）算法，該算法既有效提高了收斂速率又具備很好的抗干擾能力。同時，為了克服CLMS算法停滯等待的弊端，采用了瞬時轉移結構；另外，在參數的迭代公式中使用sign函數進行優化以降低運算量。仿真結果證明該算法與CLMS、VS-CLMS相比，在不同的仿真環境中均能表現出良好的均方特性和跟蹤特性。

自適應濾波；最小均方算法；凸組合；變步長；系統識別

網址：www.sys-ele.com

0　引　言

自適應算法被廣泛應用在噪聲對消、系統識別、時延估計等諸多方面，是信號處理技術中至關重要的部分。其中最小均方（least mean square，LMS）誤差算法是實現自適應的一種行之有效的方法，因為其實現便捷且高效的特點而被廣泛使用［16］。但是在LMS中，收斂速率和穩態誤差是一組不可調和的矛盾，這對系統實現影響很大。

近年來，為了解決這種矛盾來提高性能，推導出了各類LMS算法。文獻［4 6］是根據步長參數與誤差信號滿足不同的函數關系而提出的變步長最小均方算法。文獻［7-14］是將兩個LMS濾波器進行凸組合得到凸組合最小均方（convexcombination of least mean square，CLMS）濾波器算法，使組合濾波器系統能夠克服單個濾波器的矛盾而實現更優的性能。文獻［15-16］將變步長與凸組合進行結合得到一種變步長凸組合最小均方（variable step-size CLMS，VS-CLMS）自適應濾波算法。其中，步長參數與誤差信號滿足Sigmoid函數，在一定程度上改善了濾波器的性能，但是誤差信號在0值附近時步長變化較大，導致當系統處于穩態時依然有較大的步長，另外，Sigmoid函數的計算過程較為復雜且其收斂速率表現并不是特別明顯。因此需要對Sigmoid函數加以改進從而得到更好的性能。

上述算法在轉換階段，即系統在快速濾波器達到穩態超量均方誤差（excess mean squared error，EMSE）后停止，等待慢速濾波器達到相同的EMSE后再繼續收斂，導致收斂速率較慢。為了避免此限制，文獻［9］提出了一種基于CLMS的低復雜度權值轉讓策略，通過使用一個長度為N0的窗來實現，這個方法通過簡單賦值來完成，有效克服其弊端。

受此啟發，本文提出一種新改進的變步長凸組合最小均方算法（new variable step-size CLMS，NVS-CLMS）。該算法中大步長濾波器的步長參數與誤差信號滿足Lorentzian函數，同時加入瞬時權值轉移結構。另外，在參數a（n）的迭代公式中使用sign函數［11］，既可以降低計算量又能提高參數的穩定性。實驗結論證實該算法具備良好的收斂速率和跟蹤性能，有很大的實際應用價值。

1　VS-CLMS算法

VS-CLMS算法原理如圖1所示。由兩個相互獨立的LMS濾波器組成，其中一個設置為步長可變的濾波器來保證算法的收斂速率，另一個設置為固定小步長的濾波器來保證系統較低的穩態誤差。其中x（n）為信號輸入；y（n）為系統輸出的等效結果；d（n）為期望響應；e（n）為整個濾波器的等效誤差；w1（n）、w2（n）分別為濾波器的權值；y1（n）和y2（n）分別為兩個濾波器的輸出；e1（n）和e2（n）分別為兩個濾波器的誤差；λ（n）為CLMS算法的聯合參數。為論述方便，假設第一個濾波器是步長變化的。

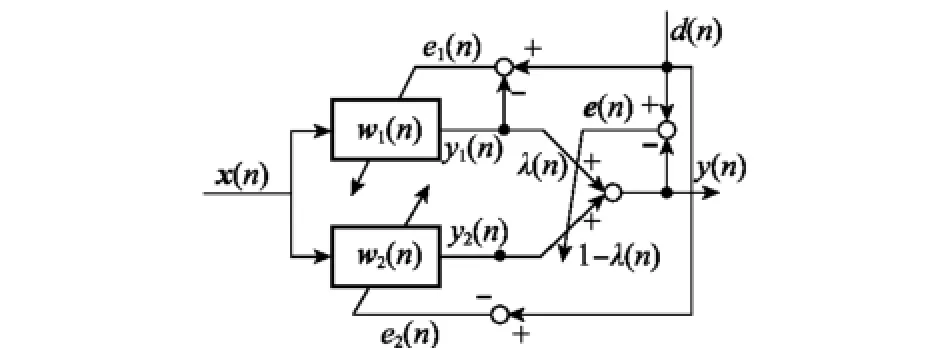
圖1　VS-CLMS算法原理圖

則濾波器系統的輸出為

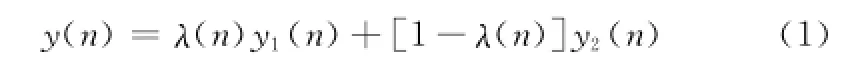
式中，yi（n）=wTi（n）x（n），i=1，2；聯合參數λ（n）∈［0，1］，定義為

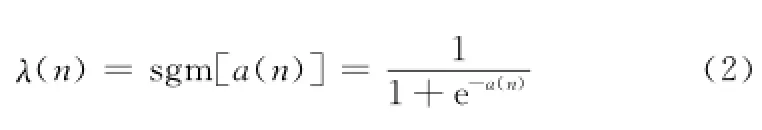
濾波器系統的等效誤差為

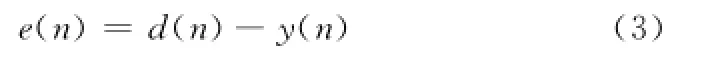
組合權值表示為

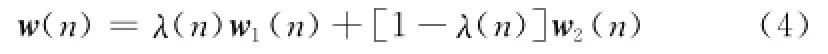
單個濾波器誤差為

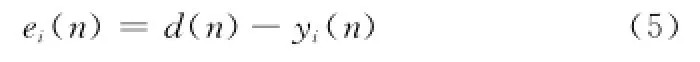
單個權值更新公式為

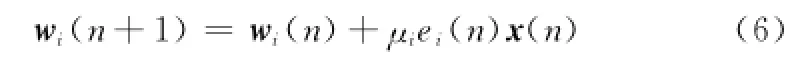
系統等效誤差表示公式為

式（2）中，參數a（n）的取值遵循LMS準則，則其迭代公式可由最速下降表達式推導得出為

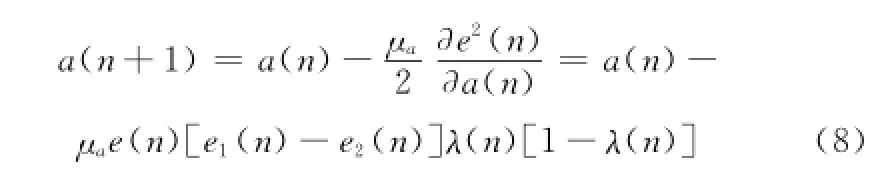
式中，μa為參數a（n）的步長因子，其取值應保證a（n）快速收斂以確保組合濾波器的輸出能夠根據期望信號穩定的實現對輸入信號的跟蹤。另外，當λ（n）的取值非常接近邊界值0或1時，式（8）中混合參數a（n）的更新停止，為了避免這個問題將a（n）的取值范圍限定為［-a+，a+］，以保證λ（n）的范圍在［1-λ+，λ+］，其中λ+=sgm（a+）是一個接近1的常數。在該限定下a（n）的更新可以有保證穩定的進行。通常a+=4，則聯合參數λ（n）的范圍為［0.018，0.982］［10］。

VS-CLMS中第一個濾波器為根據均方誤差收斂的變步長LMS獨立濾波器，步長參數μ1選取滿足Sigmoid函數［7］，其表達式：

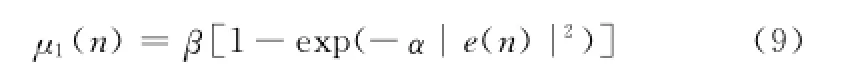
為使μ1收斂，式（9）中參數取值應滿足：α＞0，0＜β＜μmax。

從式（9）能夠看出，隨著誤差e（n）的變化，步長參數μ1（n）的取值也同時發生變化。在迭代初期，誤差e（n）通常比較大，此時需要步長參數取值接近其最大值μmax來使系統得到最快的收斂速率；隨著迭代的次數增多誤差e（n）逐漸減小并趨近于0，為得到更好的穩態性能，μ1（n）的取值也應趨向于一個較小的值。

2　改進的變步長CLMS算法

文獻［15］中提出的變步長算法，一定程度上改善了濾波器的性能，但是誤差信號在0值附近時步長變化較大，導致當系統處于穩態時依然有較大的步長，另外，Sigmoid函數的計算過程較為復雜且其收斂速率表現并不是特別明顯，需要對提出新的步長控制函數以得到更好的性能。因此，本文使用Lorentzian函數［4］來控制步長參數變化，即

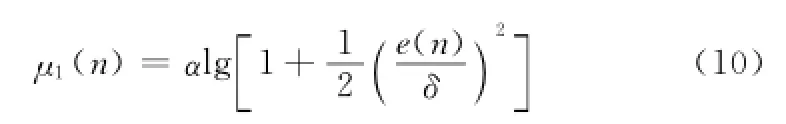
式中，α控制變化范圍；δ控制函數趨于平穩時的形狀。針對此函數，為了更好的去除外界噪聲對步長參數變化的影響，具有更好的抗干擾性，對式（10）進行進一步改進，即

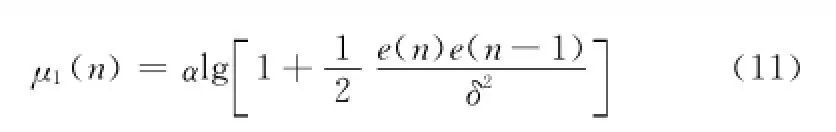
圖2為Lorentzian函數α=0.006，δ=0.001與Sigmoid函數α=0.06，β=0.04的曲線對比圖，能夠看出在圖示符合條件的范圍中，Lorentzian所對應的步長參數要大于Sigmoid，因此該改進具有更快的收斂速率和跟蹤性能，并且能夠有效抵抗系統的突變。

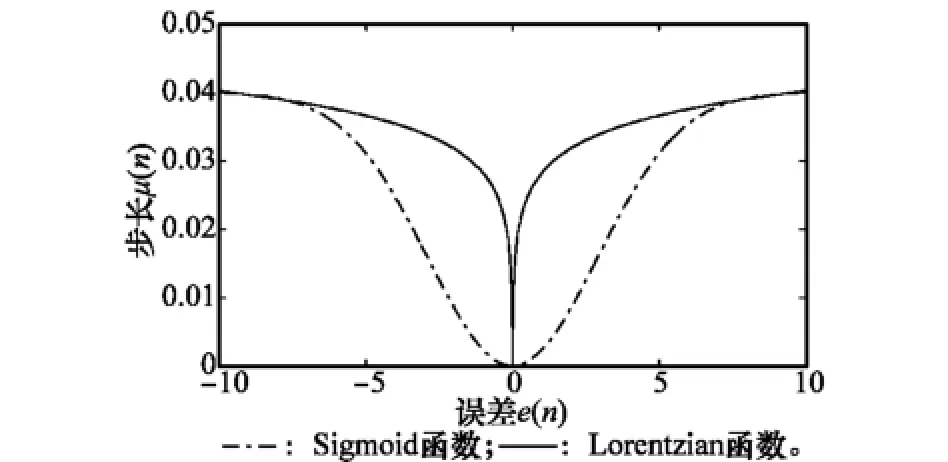
圖2　Lorentzian函數與Sigmoid函數的曲線對比圖

CLMS的計算復雜度較高很大程度上阻礙了其應用和發展。為了解決這個問題，本文采用sign函數對參數a（n）的更新式（8）進行優化［11］。

因為a（n）的更新遵循LMS準則，則其代價函數為

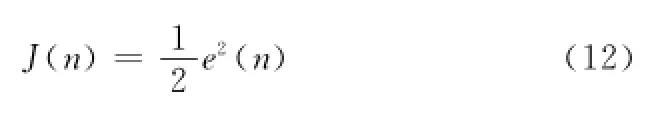
a（n）被歸一化后其代價函數的梯度可以寫作ΔaJ（n）。則a（n）的遞歸更新公式為

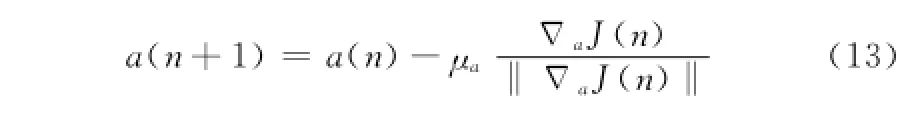
其中ΔaJ（n）的計算公式為

式中，sign（x）函數，x＞0時取值為1，x＜0時取值為-1，x=0時取值為0。

將式（15）、式（14）代入式（13）可得

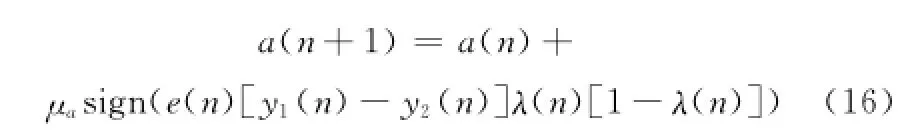
由于λ（n）與1-λ（n）始終大于零，則式（16）可以被等效的簡化為

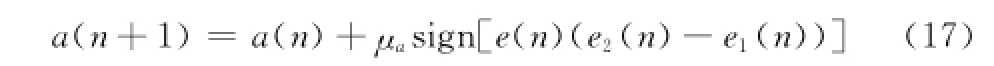
使用式（17）替代式（8）計算a（n）可以有效地降低運算量。

傳統的CLMS算法在轉換階段，變步長濾波器達到穩態EMSE之后，組合濾波器會停止收斂等待固定小步長濾波器，這種弊端極大影響系統的收斂速率。為了克服這種限制，本文采用瞬時轉移結構［9］，其通過定義一個長度為N0的窗來完成。

瞬時轉移結構的具體實現：當λ（n）的取值大于λ+，即組合濾波器的性能依賴于變步長濾波器的收斂性能時，定義一個N0的取值，使得在該階段中系統每隔N0次迭代就令慢速濾波器的權值等于變步長濾波器的權值，即令w2（n+1）=w1（n+1）。瞬時轉移結構的使用可以讓系統在達到變步長濾波器穩態后及時進入慢速濾波器的收斂階段。對于N0的取值，為了使慢速濾波器能夠實時地進行權值同步，N0的值越小越好，雖然較小的取值不會影響系統的性能但是增加了計算量，因此，為了達到良好效果通常取N0=2。

變步長CLMS的第二個濾波器為小步長的慢速收斂的，由此可以求得LMS失調為［15］

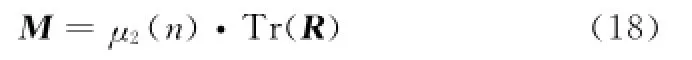
式中，M為失調因子；R為權矢量失調因子。

3　抗干擾性能分析

在LMS算法中，誤差e（n）計算公式為［4］

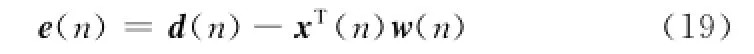
通過對式（19）移項可以計算期望響應

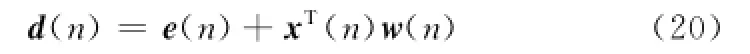
由式（20）能夠看出，誤差e（n）與系統的輸入信號x（n）相關，為了進一步進行性能分析，期望響應的另一種表達式表示為

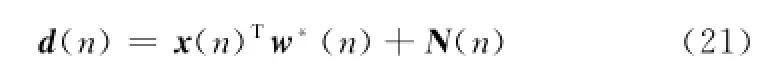
式中，N（n）為外界干擾信號，是與輸入信號x（n）相互獨立且均值為0的高斯白噪聲；w*（n）為理想權值。

令

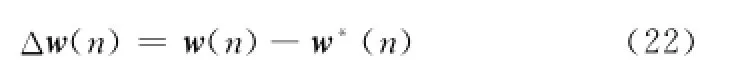
式中，Δw（n）是權值偏差。則可以得到

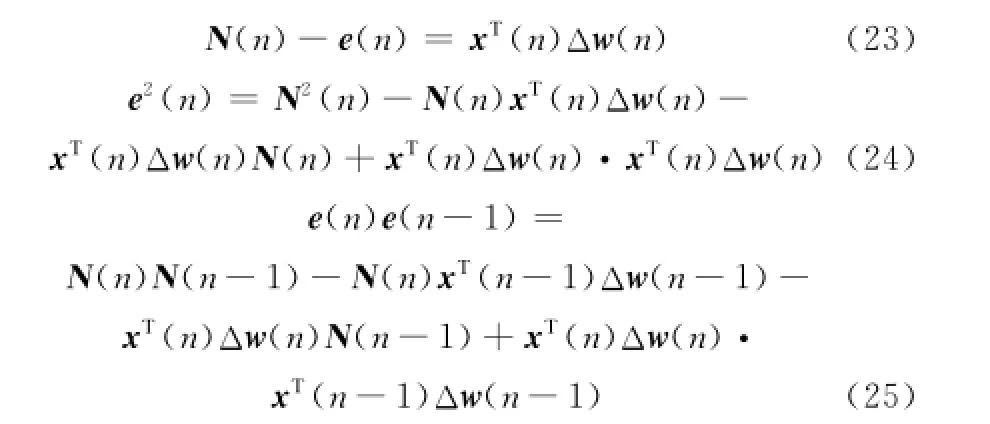
因為N（n）與x（n）相互獨立且均值為0，所以對式（24）和式（25）兩邊同時求期望并化簡后可以得到

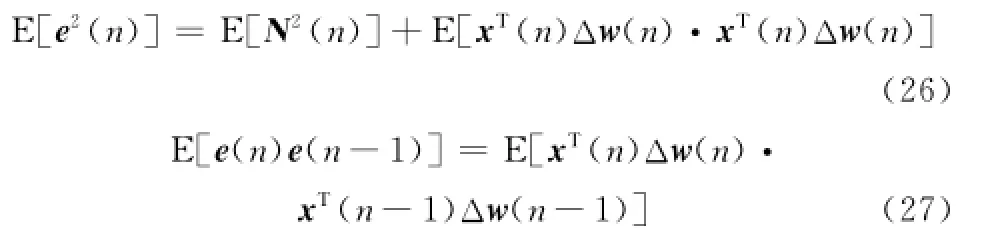
由式（26）和式（27）能夠看出，式（26）中存在E［N2（n）］，所以E［e2（n）］的取值與外界干擾信號的大小有關，當存在大幅度的干擾時會導致系統不穩定。而在式（27）中E［e（n）e（n-1）］的取值僅與輸入信號x（n）有關，外界噪聲的干擾對其沒有影響，因此其抗干擾性能較改進之前有所提高。

4　算法復雜度分析

以運算過程中每次迭代所使用乘法次數判斷濾波器算法的運算復雜度，每個部分需要的運算數統計如表1所示。

(例如，設mb= 0.3，Φ= 175，ψx= 15，[α]= 40，利用軟件Excel的規劃求解功能，可這樣求得ma= 2.508，mc= 2.194，φ0= 56.0，ψ0= 15.3。

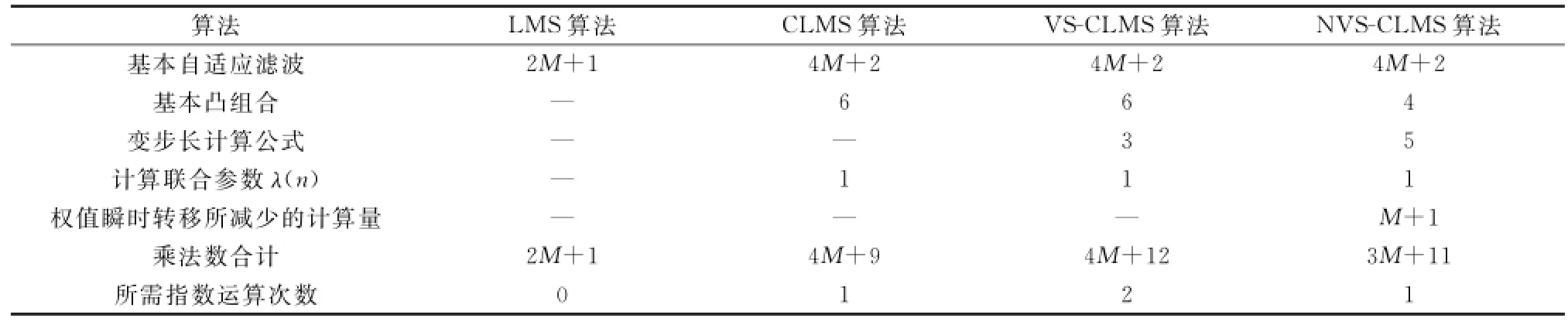
表1　不同算法計算復雜度比較

LMS、CLMS、VS-CLMS、NVS-CLMS的計算復雜度比較如表1所示，其中M為濾波器的長度。基本LMS算法需要2M+1次乘法，而CLMS、VS-CLMS、NVS-CLMS由兩個LMS濾波器組成，因此其基本計算次數為4M+2；在凸組合部分CLMS、VS-CLMS需要至少6次乘法來計算組合濾波器輸出和參數a（n）的更新，而本文的算法僅需要4次；通過函數進行變步長計算時VS-CLMS要進行3次乘法和1次指數運算，NVS-CLMS僅需要5次乘法，避免了指數運算有效較小計算量；在變步長濾波器收斂階段，本文的算法使用瞬時轉移結構直接進行權值的賦值，減小了M+1次乘法計算。

綜上，VS-CLMS計算量為4M+12次乘法和2次指數運算；NVS-CLMS在收斂階段需3M+11次乘法和1次指數運算，在變步長濾波器達到穩態后需4M+12次乘法和1次指數運算。總體來說有效減小了運算復雜度。

5　仿真實驗

為了驗證算法的性能，現將NVS-CLMS算法與傳統的CLMS算法、文獻［15］的VS-CLMS算法同時作用于系統辨識過程中并在不同的環境下分別實驗。各算法參數的選取均為其多次實驗所得的最佳值，得到的EMSE學習曲線均是200次蒙特卡羅實驗得到的平均結果。參數取值：μ1=0.025，μ2=0.002 5；NVS-CLMS中α=0.006，δ=0. 01，μa=0.17；VS-CLMS中α=0.06，β=0.05，μa=0.2；CLMS中μa=160。

5.1引入瞬時轉移結構對收斂的影響

某待測系統為10階非遞歸型濾波器模型，假定濾波器長度與模型階次值相同。輸入高斯白噪聲x（n）服從標準正態分布，同時外加干擾與x（n）相獨立且信噪比為20 dB。采樣點數為5 000，令系統在迭代至2 500點時發生突變來對比其跟蹤性能。

在上述條件下，讓本文提出的NVS-CLMS算法在使用瞬時轉移結構與不使用該結構的情況下分別仿真進行對比，以明確觀察瞬時轉移結構的作用。對比曲線如圖3所示。

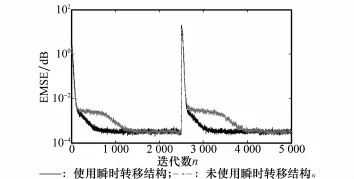
圖3　瞬時轉移結構使用對比圖

從圖3觀察得出，未使用瞬時轉移結構的算法在收斂曲線中表現出明顯的停滯，且在迭代至1 300點處才趨于平穩，而使用瞬時轉移結構的算法有效避免了傳統CLMS算法快速濾波器停滯等待的弊端，在500次迭代時就達到穩態，提高了系統的收斂速率。

5.2高斯白噪聲為輸入的仿真

在第5.1節所述情況下進行各算法仿真。EMSE學習曲線如圖4所示。

圖4　在高斯白噪聲輸入時EMSE的學習曲線

從圖4觀察得出，本文提出的NVS-CLMS算法收斂速率更快，在迭代至500步時便趨于穩定且擁有更低穩態誤差，在跟蹤性能方面相對于VS-CLMS也有明顯地提高。

5.3相關信號為輸入的仿真

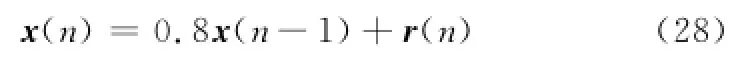
設輸入產生方程式［15］式中，r（n）是高斯白噪聲，方差為1且與系統的外加干擾信號相獨立。其他條件與第5.1節中相同。EMSE學習曲線如圖5所示。

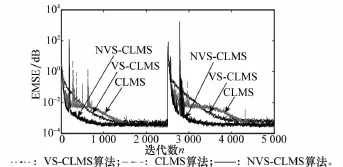
圖5　在相關信號輸入時EMSE的學習曲線

從圖5觀察得出，本文提出的算法也能很好地適用于相關信號輸入時的情況，在收斂過程中算法有突變發生對穩定性有所影響，但相比仍有良好的性能。

5.4非平穩環境下的仿真

讓各算法分別在非平穩時變系統中進行實驗［15］w（n+1）=w（n）+c（n）（29）式中，c（n）為0均值，0.01方差的高斯白噪聲。其他條件與第5.1節中相同。EMSE學習曲線如圖6所示。

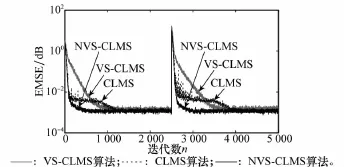
圖6　在非平穩環境下時EMSE的學習曲線

從圖6觀察得出，在非平穩環境下穩態誤差較第5.2節與第5.3節有所下降，但同VS-CLMS、CLMS算法相比，本文的NVS-CLMS性能優勢也較為明顯。

5.5抗干擾性能比較

為了更清楚地觀測NVS-CLMS和VS-CLMS算法的抗干擾性能，在第5.1節所述情況中不同信噪比下進行仿真，并分別截取兩種算法EMSE學習曲線接近收斂的部分，如圖7和圖8所示。

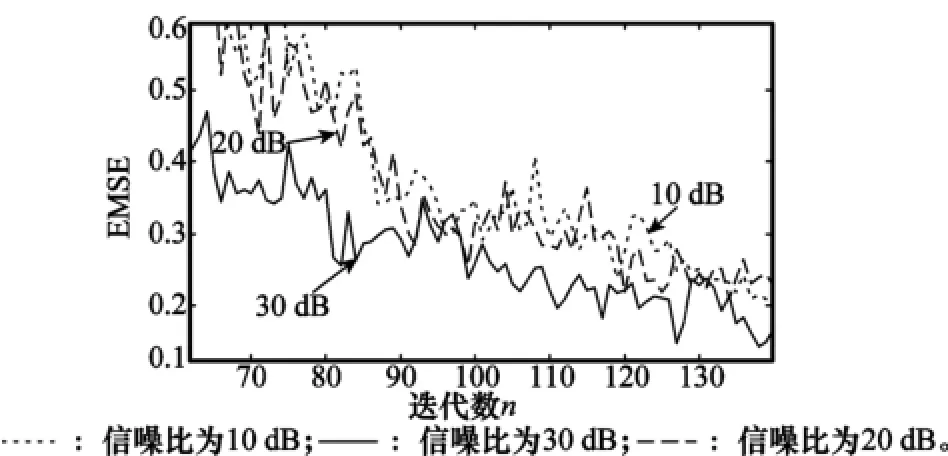
圖7　VS-CLMS算法在不同信噪比下的學習曲線

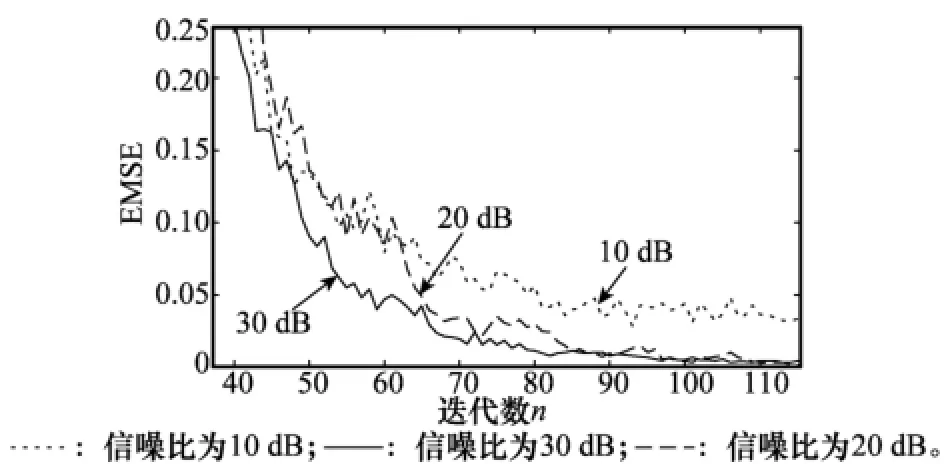
圖8　NVS-CLMS算法在不同信噪比下的學習曲線

通過比較圖7和圖8可以看出，信噪比越高濾波得到信號的誤差就越小，在各個信噪比的曲線中，圖7的波動大、振蕩劇烈，而圖8的曲線較為平滑且穩態誤差更低。因此，本文NVS-CLMS的抗干擾性能更優。

5.6實際量測數據的測試

本節利用一段實際采集的某軍用標準短波通信信號進行信道均衡的測試，信號的時域和時頻圖顯示如圖9所示。

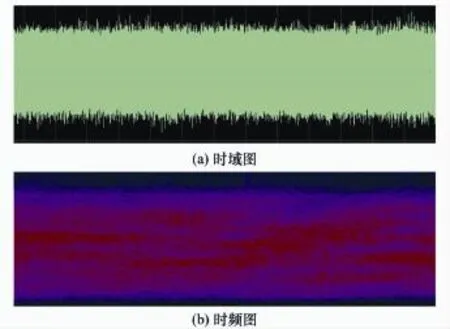
圖9　實際量測信號的時域和時頻圖顯示

該信號的調制方式為八相移鍵控（8 phase shift keying，8PSK），符號率為2 400 bps，信號頭長度為287個符號，其后的數據每隔256個未知數據符號插入了31個已知符號。

處理方法：在已知序列階段（同步頭和插入31個已知符號階段）采用自適應算法進行已知數據引導的信道均衡，在未知數據階段采用判決引導的信道均衡。為了減小同步誤差的影響，采用了頻率十分精確的本地載波，同時利用鎖相環跟蹤載波相位以及采用最大平均功率點定時同步方法。在自適應算法進行信道均衡階段采用VS-CLMS及本文提出的NVS-CLMS算法分別進行處理后得到的輸出星座圖結果如圖10和圖11所示。

通過比較圖10和圖11可以看出，在實際量測數據的測試試驗中，VS-CLMS算法以及本文改進的NVS-CLMS算法均可以較好的恢復出原信號，而NVS-CLMS算法輸出的星座圖更加清晰，每個信號點處的點更加聚集，相鄰信號點分的更開。在實際測試中通過估計信噪比得到VSCLMS算法的結果輸出為19.5 dB，而NVS-CLMS算法為21 d B，提高了1.5 d B。綜上比較，本文改進的算法在實際量測數據測試中達到了較好的效果且輸出結果更加理想，充分說明該算法的實效性。

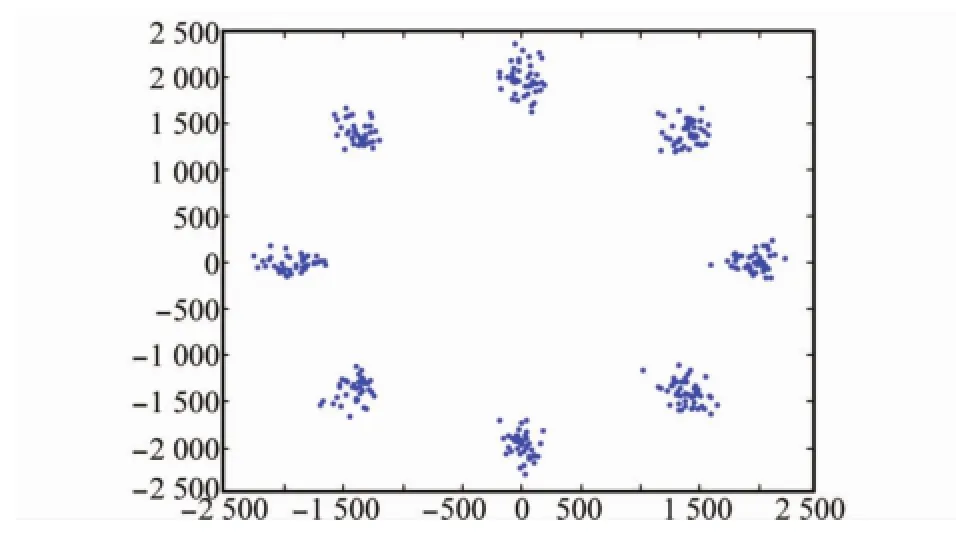
圖10　VS-CLMS算法處理得到的星座圖

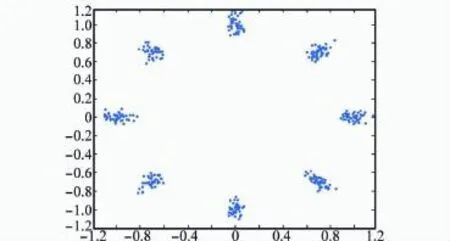
圖11　NVS-CLMS算法處理得到的星座圖

6　結　論

本文所提出的NVS-CLMS算法，采用Lorentzian函數來控制步長參數的變化有效提高了收斂速率和跟蹤性能，且進一步通過公式的改進具備了更好的抗干擾特性；另外，利用sign函數對參數a（n）的迭代公式進行改進，使新算法的計算復雜度得到了優化；在此基礎上引入瞬時轉移結構避免了CLMS算法停滯等待的弊端。NVS-CLMS算法在不同條件下仿真及在實際量測數據測試中均取得更優的性能，擁有較大的實用價值。

［1］Lopes W B，Lopes C G.Incremental combination of RLS and LMS adaptive filters in non-stationary scenarios［C］//Proc.of the International Conference on Acoustics，Speech and Signal Processing，2013：5676-5680.

［2］Tan Y，He Z Q，Tian B Y.A novel generalization of modified LMS algorithm to fractional order［J］.IEEE Signal Processing Letters，2015，22（9）：1244-1248.

［3］Meher P K，Sang Y P.Critical-Path analysis and low-complexity implementation of theLMS adaptive algorithm［J］.IEEE Trans.on Circuits and Systems，2014，61（3）：778-788.

［4］Zhang J J，Zhou F F，Xu S.Improved variable step size LMS improved algorithm［J］.Modern Electronics Technique，2014，37（1）：11-13.（張晶晶，周菲菲，許帥.改進的變步長LMS改進算法［J］.現代電子技術，2014，37（1）：11-13.）

［5］Lee H S，Kim S F，Lee J W，et al.A variable step-size diffusion LMSalgorithm for distributed estimation［J］.IEEE Trans.on Signal Processing，2015，63（7）：1808-1820.

［6］Zhang F，Wang Y，Ai B，Variable step-size MLMS algorithm for digital predistortion in wideband OFDM systems［J］.IEEE Trans.on Consumer Electronics，2015，61（1）：10-15.

［7］Azpicueta R，Figueiras-Vidal L A，Arenas-García A R.A normalized adaptation scheme for the convex combination of two adaptive filters［C］//Proc.of the International Conference on Acoustics，Speech and Signal Processing，2008：3301-3304.

［8］Silva M T M，Nascimento V H，Arenas-García J.A transient analysis for the convex combination of two adaptive filters with transfer of coefficients［C］//Proc.of the International Conference on Acoustics，Speech and Signal Processing，2010：3842-3845.

［9］Nascimento V H，De Lamare R C.A low-complexity strategy for speeding up the convergence of convex combinations of adaptive filters［C］//Proc.of the International Conference on Acoustics，Speech and Signal Processing，2012：3553-3556.

［10］Arenas-García J，Figueiras-Vidal A R，Sayed A H.Mean-square performance of a convex combination of two adaptive filters［J］. IEEE Trans.on Signal Processing，2006，54（3）：1078-1090.

［11］Lu L，Zhao H Q.A novel convex combination of LMSadaptive filter for system identification［C］//Proc.of the International Conference on Signal Processing，2014：225-229.

［12］Das B K，Chakraborty M C.Systems sparse adaptive filtering by an adaptive convex combination of the LMS and the ZA-LMSalgorithms［J］.IEEE Trans.on Circuits and Systems，2014，61（5）：1499-1507.

［13］Donmez M A，Ozkan H，Kozat S S.Transient analysis of convexly constrained mixture methods［C］//Proc.of the IEEE International Workshop，Machine Learning for Signal Processing，2012：1-5.

［14］Li N，Zhang Y G，Wang C C.A convex combination LMS algorithm based on krylov subspace transform［C］//Proc.of the 5th International Joint Conference，Computational Sciences and Optimization，2012：802-805.

［15］Yu X，Liu J C，Li H R.A convex combination of variable step-size adaptive filter and its mean-square performance analysis［J］.Acta Electronic Sinica，2010，38（2）：480-484.（于霞，劉建昌，李鴻儒.一種變步長凸組合自適應濾波器及其均方性能分析［J］.電子學報，2010，38（2）：480-484.）

［16］Hong D F，Miao J，Su J，et al.An improved variable step-size convex combination of LMSadaptive filtering algorithm and its analysis［J］.Acta Electronic Sinica，2014，42（11）：2225-2230.（洪丹楓，苗俊，蘇健，等.一種變步長凸組合LMS自適應濾波算法改進及分析［J］.電子學報，2014，42（11）：2225-2230.）

Low computational complexity variable step-size CLMS algorithm based on Lorentzian function

ZENG Le-ya1，XUHua1，WANG Tian-rui2
（1.Information and Naυigation College，Air Force Engineering Uniυersity，Xi'an 710077，China；
2.School of Geography Science，Nanjing Normal Uniυersity，Nanjing 210046，China）

In order to avoid the conflict between convergence speed and stable state error，and improve the adaptive filter algorithm，a new variable step-size convex-combination of least mean square（NVS-CLMS）algorithm is proposed by using the improved Lorentzian function.The new algorithm effectively improves convergence rate and has good anti-interference performance.Furthermore，the instantaneous transfer scheme is utilized to overcome disadvantages of CLMSand the sign function in iterative of the parameter can also reduce the computational complexity.Theoretical analysis and simulation results show that under different environments，the proposed algorithm，compared with the CLMSand VS-CLMSalgorithms，not only has a superior capability of tracking，but also can maintain a better convergence.

adaptive filtering；least mean square（LMS）algorithm；convex combination；variable stepsize；system identification

TN 911.7

A

10.3969/j.issn.1001-506X.2016.05.05

1001-506X（2016）05-0998-06

2015-06-29；

2015-10-28；網絡優先出版日期：2015-12-23。

網絡優先出版地址：http://www.cnki.net/kcms/detail/11.2422.TN.20151223.1019.012.html

國家自然科學基金（61001111）資助課題

曾樂雅（1992-），男，碩士研究生，主要研究方向為通信信號處理、自適應濾波。

E-mail：zengleya@163.com

許華（1976-），男，副教授，博士，主要研究方向為通信信號處理、盲信號處理。

E-mail：xu.hua@139.com

王天睿（1992-），女，碩士研究生，主要研究方向為信息采集與處理。

E-mail：wangtianrui0321@163.com