基于矩陣束的多波段雷達信號高精度融合成像算法

鄒永強，高勛章，黎　湘

（國防科學技術大學電子科學與工程學院，湖南　長沙 410073）

基于矩陣束的多波段雷達信號高精度融合成像算法

鄒永強，高勛章，黎湘

（國防科學技術大學電子科學與工程學院，湖南長沙 410073）

多波段信號融合技術在信號層將多個不同子帶融合成一個大帶寬信號，因而能夠有效提高雷達圖像距離分辨率。目前，基于全極點模型的融合技術主要采用root-MUSIC（multiple signal classification）及其改進算法實現極點的估計，在較弱的噪聲條件下這種方法得到了不錯的融合效果。然而在低信噪比條件下root-M USIC算法容易受到噪聲干擾而難以實現正確極點獲取，進而極大影響到最終信號融合效果。為減小噪聲影響，提出用矩陣束算法實現多波段信號極點估計，在此基礎上通過不同子帶對應極點間的相位關系估計出相干參數，同時對融合結果以信號差的2范數最小為準則進行迭代，以減小融合信號的誤差。最后采用加權尋優的方式進一步提高了信號的融合精度。仿真實驗結果表明，提出的方法有效提高了低信噪比條件下的多波段信號融合效果。

多波段信號；全極點模型；矩陣束；迭代算法；加權尋優

網址：www.sys-ele.com

0　引　言

多波段雷達融合成像技術是現有條件下獲得高分辨逆合成孔徑雷達（inverse synthetic aperture radar，ISAR）像的有效途徑［1-4］。在硬件上它僅需對幾部工作在不同頻段的寬帶雷達加裝必須的同步設備，這大大降低了獲取大帶寬雷達信號的難度，但也給目前的雷達成像算法帶來一些挑戰［5-9］，其中兩個重要的問題是多子帶信號相參補償［10-11］和寬帶信號衰減指數和模型的高精度參數估計［12］。

之所以要對不同子帶信號進行相參補償是由于參與帶寬合成的多子帶目標回波數據來自不同的雷達，即使采用高精度的時空頻同步技術［13-14］，硬件差異以及設備工作過程中的不穩定性依然會使信號間相參性變差，而雷達成像對信號相參性要求較為苛刻，如果不補償，在各子帶相參性差別不大的情況下會使融合雷達像散焦和模糊，嚴重情況下將不能成像。很多學者已經對這個問題開展研究，最早也是最詳細論述這一問題的是林肯實驗室的Cuomo［12］。他通過對多波段雷達的分析，總結得出各種因素導致的不相參最終表現為在信號上引入了一個線性相移和一個固定相移。基于此結論他提出用root-MUSIC（multiple signalclassification）和最小二乘法建立每個波段的全極點模型，而后依據該模型進行數據外推，以其中一個波段的數據為基準通過最優化的方法得到線性相移和固定相移的估計，最后進行校正。信號的高維度特點以及要同時對多個參數進行優化導致這種方法的計算量較大，同時數據外推也會帶來一定的誤差。文獻［15］提出利用目標一維像相關直接求取線性相移，并結合一個代價函數求取固定相移的方法，該方法效率較高，但受限于信號采樣數，其參數估計往往達不到理想的精度。文獻［10-11］直接根據不同子帶對應極點的表達式推導出相干參數的計算公式，該方法不需要進行外推，計算也較為簡單，但推導過程中忽略了不同子帶之間的頻帶間隔對相位的影響，同時使用root-MUSIC算法估計極點也會影響到該算法在低信噪比下的性能。

對于衰減指數和模型參數的估計，現在大多數研究將其轉化為一個全極點模型，采用模型定階方法確定極點個數k，用root-MUSIC和最小二乘法得到極點估計值，其中極點選取的是離單位圓最近的k個極點。由衰減指數和模型與全極點模型的關系可知，這些極點由于引入了衰減項導致它們會不同程度地偏離單位圓，因此root-M USIC的這種極點選擇方法本身并不是穩健的。在噪聲影響非常小的情況下能夠達到較為理想的效果，但是當噪聲較強時，一些本來偏離單位圓較遠的干擾極點可能會比真正的極點更靠近單位圓，從而導致極點選取錯誤。這個錯誤對信號融合后續所有步驟及最終結果都會產生極大影響，因此必須努力提高較強噪聲環境下極點估計的準確性。

為解決上述幾個問題，本文首先提出用矩陣束來估計極點，該方法在較低信噪比下依然能實現極點的有效估計。然后從理論上分析了相參失配信號的極點差異，既而提出不依賴于數據外推和信號采樣數的相參補償方法。之后為了提高融合信號的精度，本文先提出了一個以信號差的2范數最小為準則的多波段信號迭代融合流程，之后又提出基于各子帶和融合信號模型參數的加權尋優方法。最后用仿真數據試驗驗證了上述方法的有效性。

1　多波段雷達信號相參補償

基于前面的分析，本文針對文獻［10］方法的不足進行改進，有效提高較強噪聲條件下相干參數的估計精度。設兩部鄰近配置（同視角觀測）的雷達獨立工作，其起始頻率分別為f1，f2，頻率步進數分別為N1，N2，二者跳頻間隔均為Δf，且f2=f1+ΔB，ΔB＞Δf·N1，ΔB 為兩部雷達起始頻率間隔。對于由M個散射點構成的靜止目標，兩部雷達的基帶回波分別為

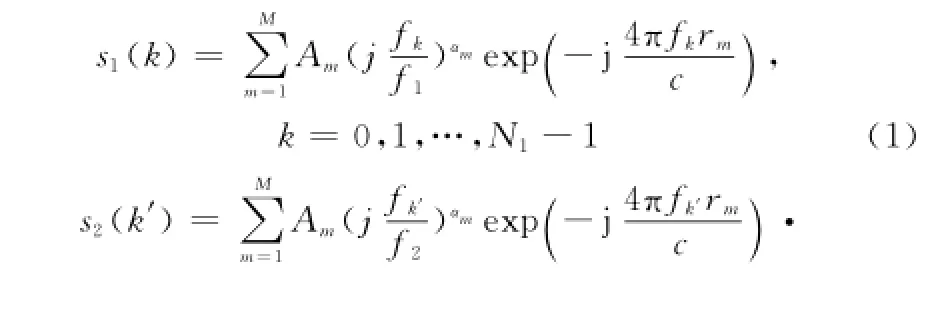
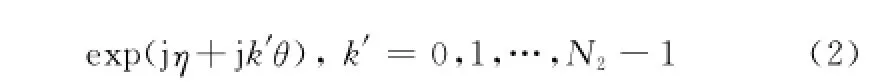
式（1）和式（2）分別是s1和s2的幾何繞射理論（geometrical theory of diffraction，GTD）模型表示，其中模型參數｛Am，rm，αm｝Mm=1表征了這M個散射中心的特性，Am是散射中心的幅度系數，rm為散射中心相對于參考點的距離，αm是0.5的整數倍，表征散射中心的幾何類型。fk=f1+k·Δf，fk′= f2+k′·Δf，c為電磁波在空氣中的傳播速度，這里近似為光速。η和θ分別為導致s1和s2不相參的固定相移和線性相移，即要估計的相干參數。

式（1）和式（2）較精確地描述了信號基帶回波，但由于頻率依賴項的存在導致其計算困難，本文采用與文獻［16］類似的方法將冪函數用指數函數近似，這樣以上兩式就轉換為式（3）、式（4）的衰減指數和模型。為便于求解還可進一步等效為全極點模型，即

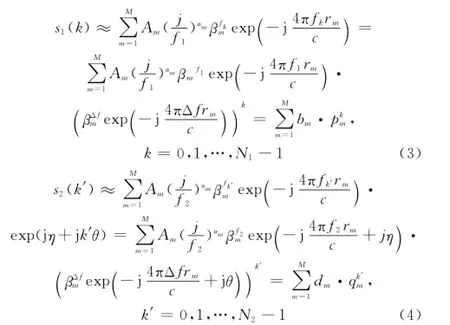
式中，用βfm代替了fαm項［16］；pm，qm分別為s1，s2的極點；bm，dm分別為s1，s2的極點對應的幅度系數。

全極點模型本質上是諧波的疊加，可用諧波分解算法求解，其中矩陣束算法是性能較優的方法。它由文獻［17］最早提出，是經典旋轉不變技術（estimation of signal parameters via rotational invariance technique，ESPRIT）的一種變形，其思路是利用指數和信號的性質，通過求解矩陣束的廣義特征值一次性地估計出指數和模型的極點［18］。文獻［16，18-19］對MUSIC、root-MUSIC、ESPRIT、矩陣束等幾種方法進行對比，從而可知矩陣束方法相對于其他幾種方法在低信噪比下有更好的性能。為此本文將用矩陣束方法對式（3）和式（4）的參數進行估計。

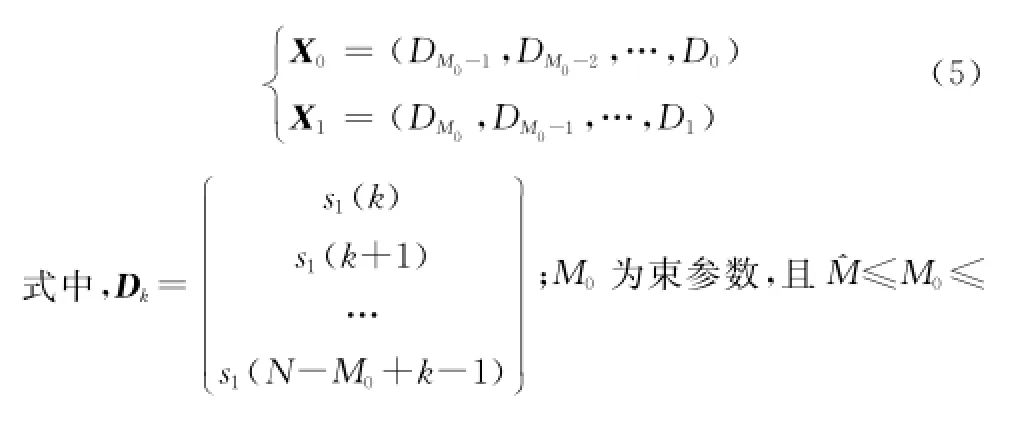
以信號s1為例，首先要構造如下Hankel矩陣，即N1-。模型階數的估計值由最小描述長度法（minimum description length，MDL）或者Akaike信息量準則法（Akaike information criterion，AIC）確定。然后對Hankel矩陣X0和X1進行奇異值分解，得

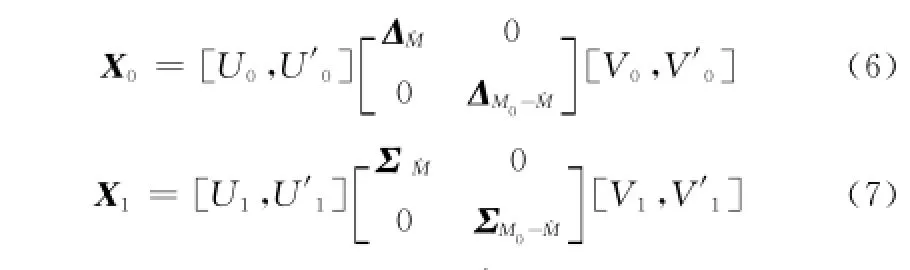
式中，Δ、Σ分別是由X0，X1的個主奇異值構成的對角矩陣，它們以及與其對應的U0、V0、U1、V1包含信號信息和少量噪聲信息；ΔM0-、ΣM0-分別是X0，X1的M0-個非主奇異值構成的對角矩陣，它們以及與其對應的U′0、V′0、U′1、V′1只包含噪聲信息。為減少噪聲，令

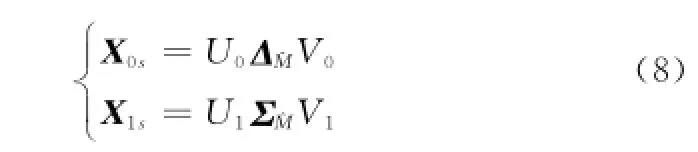
求出矩陣束X1s-λX0s的個廣義特征值即可得到極點的估計。

Vandermonde矩陣。

通過上述矩陣束方法求得的s1、s2的極點分別為

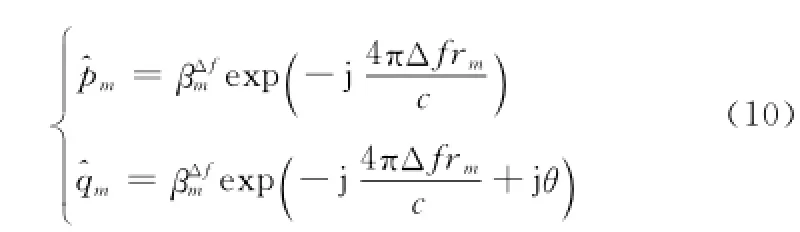
由式（10）可知，s1和s2同階極點的相角只相差一個線性相位θ。因此，θ可由式（11）估計得到

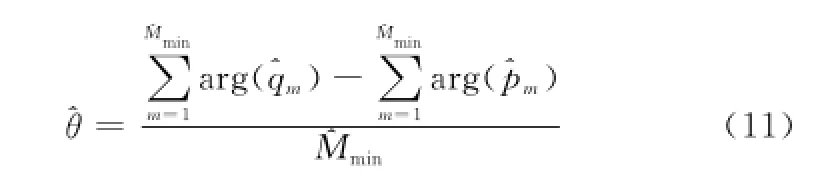
相應的，用矩陣束方法得到的同階極點的幅度估計值為

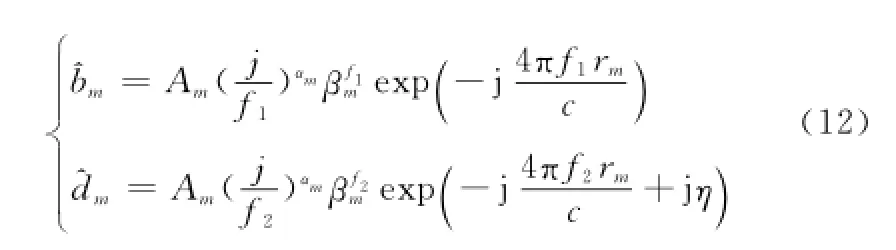
與估計線性相位的情況不同，這兩個信號同階極點的幅度所對應的相角不僅僅相差一個固定相移η，它還與頻率、相對距離rm以及散射中心類型參數αm有關，即

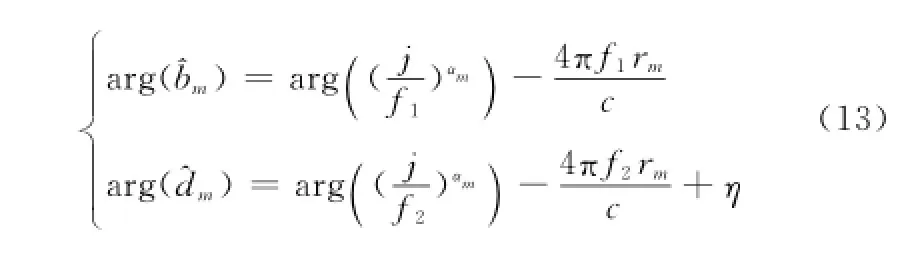
上面的參數估計中沒有對αm進行估計，所以這里無法知道的數值，但是仔細分析后可知

又f2=f1+ΔB，所以由式（15）可以得到固定相移的估計，即

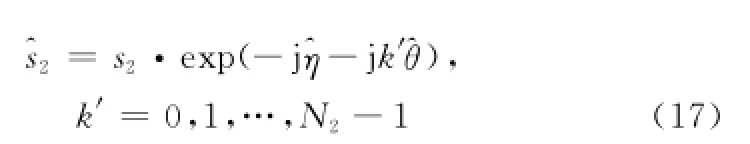
本方法從兩個方面保證了較高的相干參數估計精度：一是采用抗噪性能好的矩陣束方法估計全極點模型參數，這使得參數的估計受到噪聲的干擾減小，估計結果也更穩健。二是本方法不需要對數據進行外推，從而減少了數據外推可能帶來的誤差。另外由于沒有用到多個參數的最優化方法，本算法的計算量也較小。

2　多波段雷達信號融合成像

文獻［10-11］用缺失數據幅度相位估計（gapped-data amplitude and phase estimation，GAPES）算法填充缺失數據，然后對全頻段數據用root-MUSIC算法估計模型參數來實現數據的預測，仿真實驗得到了較為清晰的融合圖像。但是該算法沒有將融合結果反饋到參數估計中，而且其中的GAPES擬合數據本身存在較大誤差，這些都會影響融合效果。為此本文在上一節算法基礎上提出基于矩陣束的多波段信號高精度融合算法，該算法用矩陣束算法估計全頻帶的全極點模型參數（本文中的全頻段是指子帶與通過融合方法得到的頻段的總和），繼而實現空缺頻帶的數據預測。同時本算法對數據預測結果進行評判，根據結果進行迭代，然后又引入基于子帶和融合信號參數的加權尋優，進一步提高信號融合精度。以頻帶間隔ΔB的兩個子帶信號s1、s2（二者數據長度分別為N1、N2，全頻段數據總長度為N）融合為例，該算法詳細步驟如下：

步驟1用上一小節的相參補償算法對兩個子帶進行相參補償，得到相參的子帶信號s1和，為方便表述，令s2=，即用s2代表已經和s1相參的子帶信號。

步驟2基于相參子帶數據估計全頻段全極點模型參數。

設全頻段全極點模型為

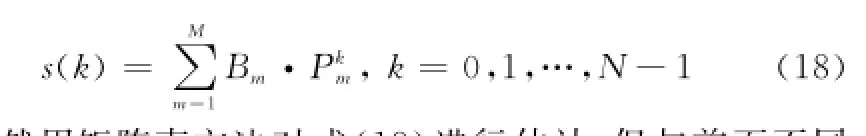
依然用矩陣束方法對式（18）進行估計，但與前面不同的是信號由頻帶上相差ΔB的兩段信號組成，為了能夠應用矩陣束算法，令

之后的步驟可參照上一節進行。

步驟3得到各階極點及其幅度的估計后可按照式（21）得到全頻段數據的估計。

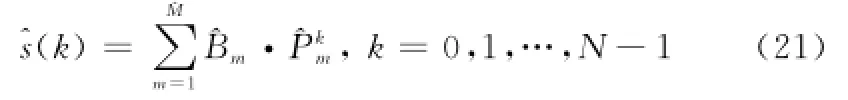
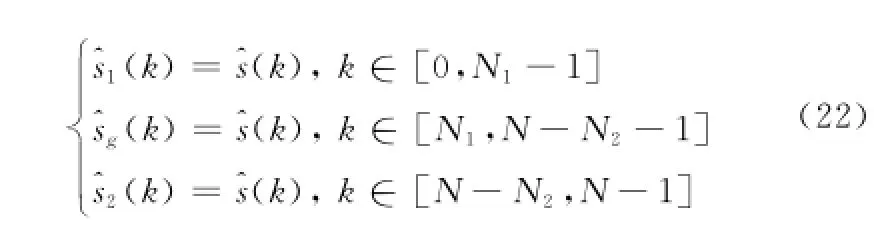
為減小估計誤差應盡量使用原始的測量數據，那么全頻段的融合信號為

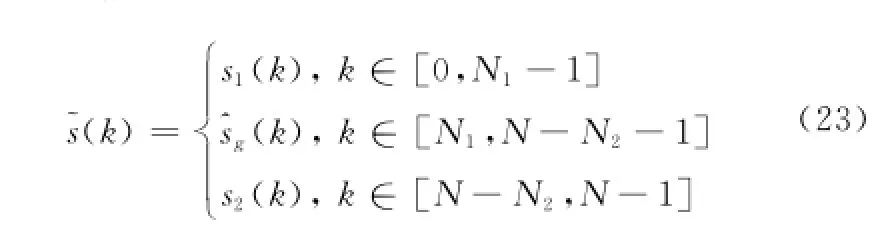
步驟4算法中引入迭代以提高信號融合質量。

各子帶的估計信號與原始測量信號的差能反映出全極點模型與測量數據的近似程度，但這個差是復向量的形式，為便于比較本文取其2范數作為衡量融合效果的標準。

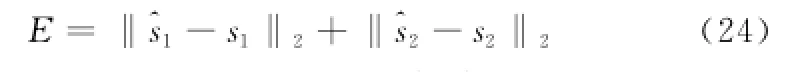
步驟5加權尋優。

由于全頻段融合數據的極點和幅度僅由不重疊的兩段數據預測而來，缺少中間空缺頻段的數據，所以就會產生因信息不全導致的誤差。這個誤差通過上面的迭代方法還不能完全消除，這里我們通過加權尋優的方式來進一步減小這個誤差。

設加權后的全頻段極點的幅度和相角分別為

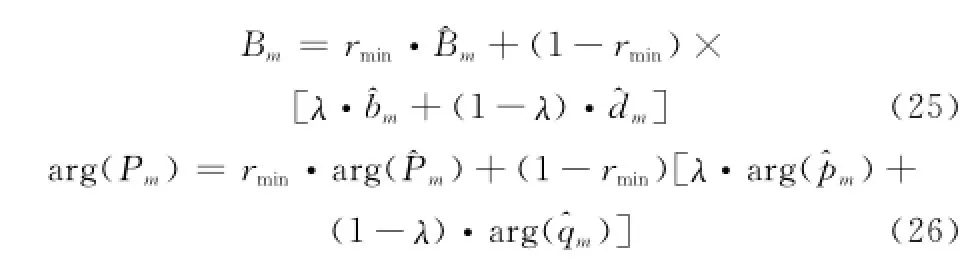
式中，r為相似系數，其定義為

那么，L=｛λ（k）|k∈K｝就是能夠提高融合精度的λ值的集合。由于L中的值可能不止一個，而且rk1，rk2往往不能同時達到最大值，所以為了均衡起見，本文選擇λ（kopt）作為最佳的加權值，其中kopt由式得到。

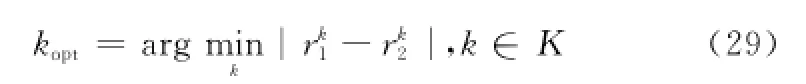
將λ（kopt）代入到式（25）和式（26）中，就可以得到最佳的極點和幅度估計，繼而獲得最佳全頻段融合信號。

總結以上步驟并考慮到實際信號的情況，本文多頻段信號融合算法主要流程如圖1所示。在相參補償之前還加入了一些步驟主要是因為目前大多數寬帶雷達發射的都是線性調頻信號，目標回波要經過dechirp處理才得到類似式（1）的基帶信號。同時，為了滿足融合成像的需要，還必須對信號進行平動補償和初相校正。

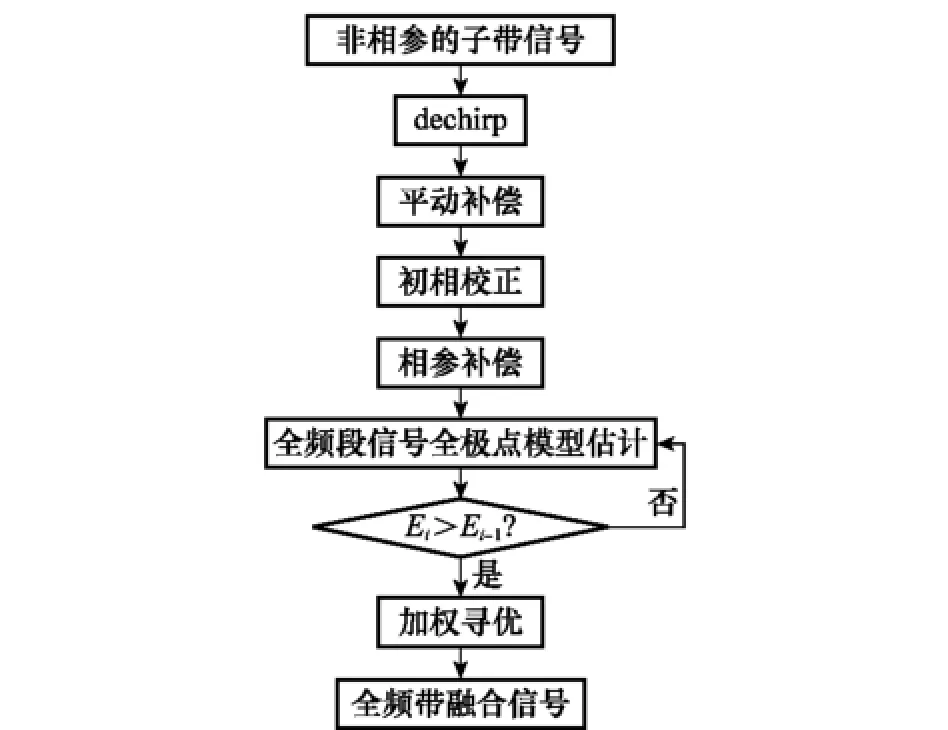
圖1　基于矩陣束的多頻段信號融合流程

對最后得到的全頻段融合信號進行脈沖壓縮就可以得到全頻段的一維像，二維像只需在一維像的基礎上進行橫向壓縮即可。

3　仿真實驗與分析

為檢驗算法性能，首先用本文提出方法（簡稱算法1）、文獻［12］的方法（簡稱算法2）和文獻［10］的方法（簡稱算法3）對基于GTD模型的仿真數據進行相參補償和信號融合實驗。之后進一步測試算法，在彈頭模型的CST2012電磁計算數據中加入不同信噪比高斯白噪聲，用上述3種算法對含噪信號融合成像。

3.1多波段雷達信號相參補償及融合實驗

本實驗中雷達的起始頻率為f0=8 GHz，跳頻間隔Δf= 10 M Hz，頻率步進數N=300，總的帶寬B=3 GHz，則理論距離分辨率為0.05 m。目標由3個離散的散射中心組成，參考距離Rref=15 km，各點的其他參數如表1所示。

表1　各散射點參數設置

那么目標的含噪回波為

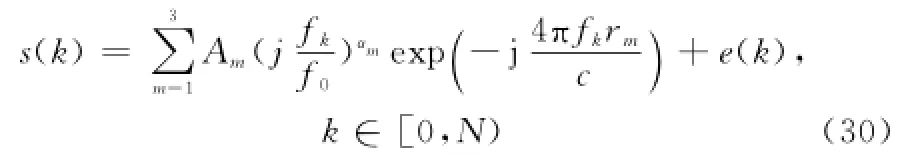
式中，k∈N+，fk=f0+kΔf，e（k）是零均值高斯白噪聲。令

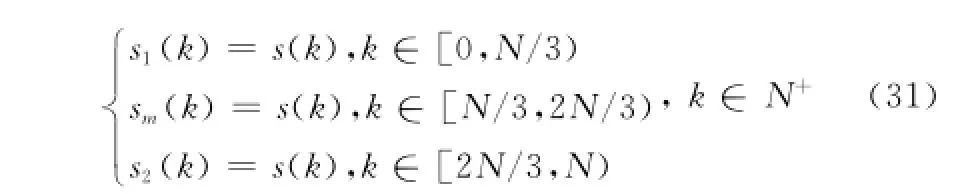
在s2中加入固定相移η=π/8和線性相移θ=π/9以模擬信號間不相參，因此得到s′2（k）=s2（k）exp（jη+j kθ）。在信噪比為1～20 dB條件下，分別用上述3種算法估計固定相移和線性相移。圖2給出了經100次蒙特卡羅仿真后，非相參量估計值的均方根誤差（root mean square error，RMSE）隨信噪比的變化曲線。從中可以看出3種算法的RMSE都隨著信噪比的降低而不同程度的變大，其中本文方法的估計精度最高，而且誤差的波動相對于其他兩種算法比較平緩，這一方面是由于本文算法沒有帶寬外推從而減少了這一因素可能帶來的誤差，另一方面是矩陣束算法本身具有較好的抗噪能力。可見本文方法確實提高了非相干參數的估計精度。

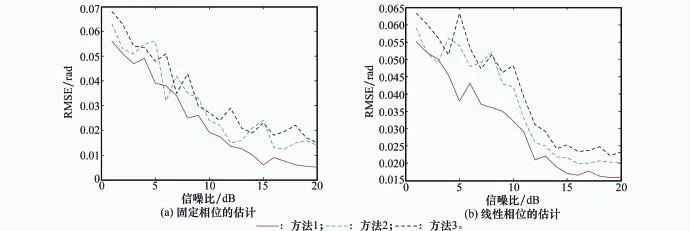
圖2　非相干參數估計誤差分析

在信噪比為15 d B的條件下，用相參補償后的s1、s2作為低、高頻帶，用3種算法來估計sm，進而實現頻帶融合。圖3是3種算法得到的sm估計值與原始信號的對比，其中圖3（a）、圖3（d）分別是算法1的初始估計結果和迭代后的最終結果。從圖3中可知，這3種算法得到的缺失頻帶信號與原始信號大部分頻段都可以擬合，但是有些頻段擬合的效果較差。總體來看，在信噪比為15 dB的條件下算法1的初始估計結果優于其他算法，但與原始信號相比仍有較大誤差，而通過迭代和加權尋優后估計誤差明顯減小。這說明算法1采用的矩陣束算法參數估計精度較高，同時迭代和加權尋優的引入確實提高了數據的估計精度。

將算法1最終估計到的空缺頻帶信號按式（31）的形式與s1、s2組成全頻帶融合信號，它與原始測量數據s的波型及一維像如圖4所示。

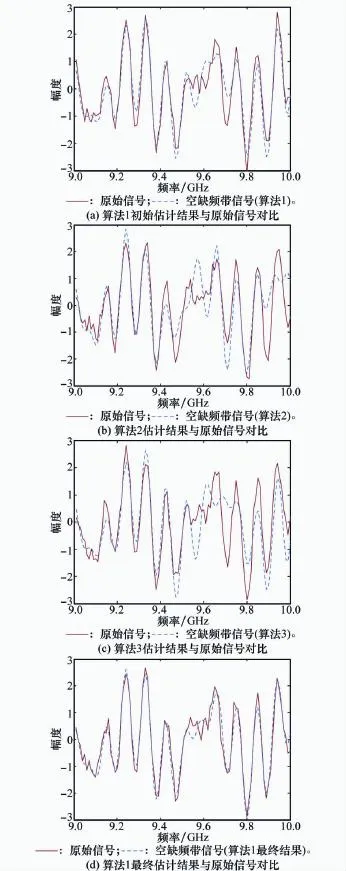
圖3　空缺頻帶估計結果

可見融合信號與原始信號實現了較好的擬合，而且由于帶寬的增加，全頻帶融合信號的一維像將3個點全部分開（上面的各子帶信號由于帶寬只有1 GHz，導致了第1、第2散射中心無法分開），達到了提高分辨率的預期效果。

3.2多頻段融合的二維ISAR像

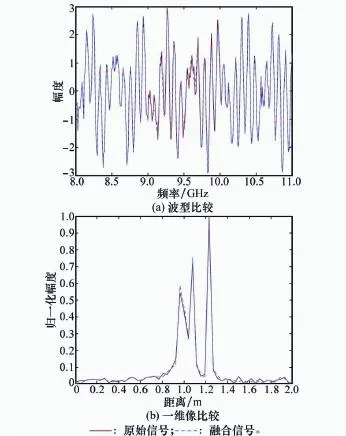
圖4　本文算法最終融合效果

本文用電磁計算軟件CST2012建模并計算模型不同方位角下的掃頻數據。該模型是由一個半球和兩個圓臺組成的簡易彈頭（見圖5（a）），其各部分的參數如表2所示。實驗中彈頭的方位角規定如下，彈頭頂端正對雷達時其方位角為0°，逆時針旋轉為正，順時針旋轉為負。計算開始前參數設置為：方位角0°～10°，角度間隔0.1°，頻率10～14 GHz，頻率間隔20 M Hz。記所得到的信號矩陣為X，則其任意元素xi，j的角標應滿足i∈［1，201］，j∈［1，101］。用距離-多普勒算法成像即可得到如圖5（b）所示結果。

表2　彈頭模型參數

為模擬兩部雷達的回波X1和X2，本文對X的數據進行分配

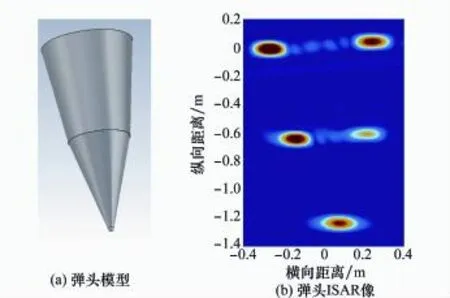
圖5　彈頭模型及其二維ISAR像

由式（32）可知，模擬的兩部雷達頻帶范圍分別為10～11 GHz和13～14 GHz。它們所成的二維ISAR像如圖6所示。由于帶寬較窄，圖6的兩幅圖像的距離向分辨率均不高，確定強散射點的精確位置比較困難。

圖6　低、高頻段二維ISAR像

為檢驗算法整體性能，在X2中加入固定相移η=π/8和線性相移θ=π/9，然后在X中分別加入信噪比為15 d B和10 dB的高斯白噪聲，用前面的3種算法進行多波段融合處理，最后用距離多普勒（range-Doppler，R-D）算法成像，所得結果如圖7和圖8所示。

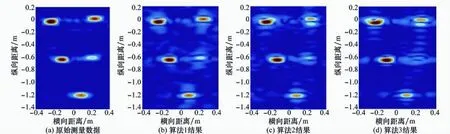
圖7　信噪比為15 dB時融合結果對比

信噪比為15 dB條件下，與圖6相比圖7（b）～圖7（d）中的融合圖像分辨率明顯提高，大多數散射點的位置能夠較為精確的給出。與圖7（a）相比，各融合圖像散射點出現了不同程度的散焦，導致一些散射點模糊。其中圖7（d）有一個散射點十分模糊，已經不能分辨。圖7（c）的各個散射點雖然都可以分辨，可是散射點周圍有較強的虛影。圖7（b）與圖7（c）、圖7（d）相比散射點能量相對集中，它與圖7（a）最為接近。

在信噪比為10 dB的條件下，含噪原始測量數據成像依然較為清晰，但融合圖像受噪聲影響較大。圖8（c）～圖8（d）的分辨率相對于圖6有一定提高，然而它們的虛假散射點數量多且能量較強，難以區分真假散射點。圖8（b）也存在類似的情況，但其散焦不是很嚴重，各個散射點較容易分辨。

為了更好的對比試驗結果，本文計算出圖7、圖8中每幅ISAR像的圖像熵［20］，其結果如表3所示。

圖8　信噪比為10 dB時融合結果對比

表3　ISAR的圖像熵

以上實驗結果可知，在信噪比為15 dB時，3種融合算法差別不大，但因矩陣束抗噪性能優于root-MUSIC以及迭代和加權尋優過程的引入導致本文方法融合效果較好。在信噪比降低到10 d B時，雖然各融合圖像質量都有較明顯下降，但是算法1得到的圖像明顯好于其他2幅，本文算法的優勢進一步體現。

4　結　論

本文在估計全極點模型參數時用矩陣束算法代替了通常使用的root-MUSIC算法，保證了較低信噪比條件下參數的估計精度。同時在融合過程中引入基于信號差2范數的迭代流程和基于各子帶及融合信號參數的加權尋優過程，進一步提高了融合信號的質量。與其他融合算法的對比實驗表明，本文提出的方法能較好保證低信噪比下的融合信號精度。但是從實驗結果中也可以看出噪聲對融合結果影響很大，雖然本文采用噪聲環境下性能優異的參數估計算法，但是依然無法徹底消除噪聲的不利影響。如果能在融合流程前提高信號的信噪比，相信會得到更好的融合效果。

［1］Chen L，Chen J.High resolution radar imaging using bandwidth extrapolation［C］//Proc.of the 3rd International Congress on Image and Signal Processing（CISP），2010：3591-3595.

［2］Sacchi M D，Ulrych T J，Walker CJ.Interpolation and extrapolation using a high-resolution discrete Fourier transform［J］.IEEE Trans. on Signal Processing，1998，46（1）：31-38.

［3］NaishadhamK，Piou J E.State-space spectral estimation of characteristic electromagnetic responses inwideband data［J］. IEEE Trans.on Antennas and Wireless Propagation Letters，2005，4：406-409.

［4］Wang Q，Wu R B，Xing M D，et al.A new algorithm for sparse aperture interpolation［J］.IEEE Trans.on Geoscience and Remote Sensing Letters，2007，4（3）：480-484.

［5］He F Y，Xu X J.High-resolution imaging based on coherent processing for distributed multi-band radar data［J］.Progress in Electromagnetics Research，2013，141（4）：383-401.

［6］Xu X J，Li J.Ultrawide-band radar imagery from multiple incoherent frequency subband measurements［J］.Journal of Systems Engineering and Electronics，2011，22（3）：398-404.

［7］Van Dorp P，Ebeling R，Huizing AG.High resolution radar imaging using coherent multiband processing techniques［C］//Proc.of the IEEE Conference on Radar，2010：981-986.

［8］Tian J H，Sun J P，Wang G H，et al.Multiband radar signal coherent fusion processing with IAA and ap FFT［J］.IEEE Trans. on Signal Processing Letters，2013，20（5）：463-466.

［9］Ba X R，Zhou F，Wang Q，et al.Sparse subband imaging of space targets in high-speed motion［J］.IEEE Trans.on Geoscience and Remote Sensing，2013，51（7）：4144-4154.

［10］Tian B，Chen Z P，Xu S Y.Sparse subband fusion imaging based on parameter estimation of geometrical theory of diffraction model［J］. IET Radar，Sonar and Naυigation，2014，8（4）：318-326.

［11］Tian B，Liu Y，Xu S Y，et al.Multi-band fusion imaging based on high precision parameter estimation of geometrical Theory of diffraction model［J］.Journal of Electronics&Information Technology，2013，35（7）：1532-1539.（田彪，劉洋，徐世友，等.基于幾何繞射理論模型高精度參數估計的多頻帶合成成像［J］.電子與信息學報，2013，35（7）：1532-1539.）

［12］Cuomo K M，Piou J E，Mayhan J T.Ultra-wideband coherent processing［J］.IEEE Trans.on Antennas and Propagation，1999，47（6）：1094-1107.

［13］Yang Y，Blum R S.Phase synchronization for coherent MIMO radar algorithms and their analysis［J］.IEEE Trans.on Signal Processing，2011，59（11）：5538-5557.

［14］Sun P L，Tang J，He Q，et al.Cramer-Rao bound of parameters estimation and coherence［J］.IET Radar，Sonar and Naυigation，2013，7（5）：553-567.

［15］Fu R W，Zhang C，Li X，et al.Research on multi band radar fusion of one dimensional super resolution imaging technology［J］. Progress in Natural Science，2006，16（10）：1310-1316.（付耀文，張琛，黎湘，等.多波段雷達融合一維超分辨成像技術研究［J］.自然科學進展，2006，16（10）：1310-1316.）

［16］Gao X Z.High resolution radar imaging based on higher-order statistic［D］.Changsha：National University of Defense Technology，2004.（高勛章.基于高階統計量的雷達目標高分辨成像研究［D］.長沙：國防科技技術大學，2004.）

［17］Hua Yin-bo，Sarkar T K.Matrix pencil method for estimating parameters of exponentially damped/undamped sinusoids in noise［J］.IEEE Trans.on Acoustics，Speech and Signal Processing，1990，38（5）：814-824.

［18］Sarkar T K，Pereira O.Using the matrix pencil method to estimate the parameters of a sum of complex exponentials［J］. IEEE Antennas and Propagation Magazine，1995，37（1）：48-55.

［19］Roy R，Paulraj A，Kailath T.Comparative performance of ESPRIT andMUSIC for direction-of-arrival estimation［C］//Proc.of the IEEE International Conference on Acoustics，Speech，and Signal Processing（ICASSP），1987（12）：2344-2347.

［20］Gao Q，Xue L，Wang Z N，et al.Imaging processing method for linear array ISAR based on image entropy［J］.Computer Engineering and Applications，2012，48（32）：125-128.（高強，薛樂，王振楠，等.基于圖像熵的線性陣列ISAR成像處理方法［J］.計算機工程與應用，2012，48（32）：125-128.）

Multiband radar signal high precision fusion imaging method based on matrix pencil algorithm

ZOU Yong-qiang，GAO Xun-zhang，LI Xiang
（School of Electronics Science and Technology，National Uniυersity of Defense Technology，Changsha 410073，China）

The multiband signal fusion technique can improve the range resolution of the radar image efficiently by fusing several subbands to a great wide band signal in the signal level.At present，the all-pole model based fusion algorithms mainly apply the root-multiple signal classification（MUSIC）and its modified method to estimate the signal poles，and good results are obtained in weak noise conditions.However，the root-MUSIC method which is fragile in noise could not easily get proper poles in low signal-to-noise ratio（SNR）.In order to eliminate the influence of noise，a matrix pencil algorithm based method is proposed to estimate the multiband signal poles.And then the coherent parameters of multiband signals are calculated through the relation of corresponding poles.At the same time，an iterative algorithm which aims to minimize the 2-norm of signal difference is introduced to reduce signal fusion error.Apart from that a weighted optimization method is also presented to improve the fusion precision.Applications to simulate dada verify that the proposed method could get better fusion results at low SNR.

multiband signal；all-pole model；matrix pencil；iterative algorithm；weighted optimization

TN 95

A

10.3969/j.issn.1001-506X.2016.05.08

1001-506X（2016）05-1017-08

2015-04-22；

2015-09-28；網絡優先出版日期：2016-02-04。

網絡優先出版地址：http://www.cnki.net/kcms/detail/11.2422.TN.20160204.1506.002.html

國家杰出青年科學基金資助項目（61025006）資助課題

鄒永強（1986-），男，博士研究生，主要研究方向為雷達成像、數據融合、雷達自動目標識別。

E-mail：zouyongqiangnudt@yeah.net

高勛章（1972-），男，教授，博士，主要研究方向為信息融合、自動目標識別、雷達信號處理。

E-mail：gaoxunzhang@nudt.edu.cn

黎湘（1967-），男，教授，博士，主要研究方向為雷達系統與信號處理、非線性信號處理、雷達自動目標識別。

E-mail：xiangli@nudt.edu.cn