高超聲速飛行器的離線雙模預測控制方法

高海燕，蔡遠利，馬　宇

(西安交通大學 電子與信息工程學院，西安　710049)

?

高超聲速飛行器的離線雙模預測控制方法

高海燕，蔡遠利，馬宇

(西安交通大學 電子與信息工程學院，西安710049)

針對預測控制在高超聲速飛行器控制中面臨的在線計算時間問題，提出了離線雙模預測控制方法。首先采用LQR方法設計無約束反饋控制增益，然后根據計算得到的控制增益和高超聲速飛行器的約束條件計算多面體不變集，根據多參數二次規劃解的性質將多面體不變集進行區域劃分并計算相應區域的自由控制變量。在線時只需要搜索當前時刻狀態所處的分區，極大地減小了在線計算時間，為高超聲速飛行器的實時控制提供了保證。仿真試驗表明，提出的方法在保持在線算法的控制性能的同時，極大減少了仿真運行時間，實現了高超聲速飛行器的實時控制。

高超聲速飛行器；雙模預測控制；多參數二次規劃；多面體不變集

0　引言

高超聲速飛行器因其重要的軍事意義，已成為世界航空航天領域極其重要的發展方向[1]。由于固有的非線性、強耦合、快時變、不確定性等特點，高超聲速飛行器控制器設計成為國內外研究熱點[2]。高超聲速飛行器飛行速度快、范圍廣，氣動特性和飛行動力學特性變化劇烈，參數存在較強的不確定性，攻角和舵偏等受到嚴格的約束條件限制[3]。因此，對飛行控制系統有較高的要求，其控制系統必須能夠保證輸入和狀態在給定的約束條件內并具有較強的魯棒性。

近年來，一些先進的控制策略被應用到高超聲速飛行器的控制中，如魯棒控制[4-5]、模型參考控制[6]、自適應控制[7]、自適應滑模控制[8]、反步控制[9]和參考輸出跟蹤控制[10]等。這些方法在不同方面改進了魯棒跟蹤性能，但均不能在設計控制器時考慮控制和狀態的約束，只能通過參數調節或通過設置參考軌跡的變化速率來保證輸入和狀態在給定的工作范圍內，并且通常是以犧牲部分控制性能為代價的。預測控制方法由于在設計控制器時就考慮控制和狀態的約束，近年來在高超聲速飛行器的控制器設計中得到越來越多的重視[11-13]。但預測控制依賴于系統的當前狀態，需要反復在線優化計算，只能應用于問題規模較小或系統的動態變化不是很快的情況。對于高超聲速飛行器這樣的高動態系統，不能達到實時控制的要求。在已有的高超聲速飛行器預測控制器設計中，文獻[11]雖然在保證約束條件限制的同時具有良好的控制性能，但沒有考慮預測控制的在線計算時間問題。文獻[12-13]雖然通過反饋線性化得到解析形式的預測控制律，在線時無需進行優化求解，可滿足高超聲速飛行器的實時控制要求，但在控制律設計中需要求解輸出的高階導數，過于復雜。

針對預測控制的在線計算時間問題，文獻[14]提出高效魯棒預測控制，通過離線設計控制增益、人為引入自由變量減少在線優化的約束條件，從而達到減小在線計算時間的目的。但該方法在考慮控制和狀態約束時采用的是橢圓不變集的方式，而實際的約束條件一般是多面體形式的，因此帶來一定的保守性。針對這樣的問題，文獻[15]提出了基于多面體不變集的雙模預測控制方法。該方法克服了橢圓不變集的保守性，但在計算控制律時還是要求解一個在線優化問題，所以仍然需要較多的計算時間。

本文根據多參數二次規劃解的性質[16](解是關于參量的分段仿射函數)，提出適用于高超聲速飛行器的基于多參數二次規劃的離線雙模預測控制方法。首先在平衡點進行小擾動線性化得到用于控制器設計的預測模型，然后離線設計無約束控制增益，根據系統約束條件和控制增益計算相應的多面體不變集。根據多參數二次規劃解的性質將多面體不變集進行分區并計算相應的自由控制變量。在線時，搜索當前時刻狀態所處的分區，得到相應的控制自由變量，作用到高超聲速飛行器的非線性模型，仿真結果驗證了方法的有效性。

1　高超聲速飛行器縱向模型

不失一般性，考慮高超聲速飛行器縱向運動，其典型的非線性運動模型可表示為

(1)其中

L=0.5ρV2SCL；D=0.5ρV2SCD；T=0.5ρV2SCT

r=h+R

CL=0.620 3α

CD=0.645α2+0.004 337 8α+0.003 772

CM(α)=-0.035α2+0.036 617α+5.326 1×10-6

CM(δe)=ce(δe-α)

式中V為速度；γ為彈道傾角；h為飛行高度；α為攻角；q為俯仰角速率；β(節流閥開關)和δe(升降舵偏轉角)為控制量；其他參數，如轉動慣量Iyy、質量m、地球半徑R等，見文獻[8]。

控制目標是利用舵面的偏轉和發動機節流閥的開關，使飛行器的速度和高度跟蹤參考指令信號。

2　基于多參數二次規劃的離線雙模預測控制

2.1基于多面體不變集的雙模預測控制

考慮線性時不變系統

(2)

其中，x∈Rn、u∈Rm分別為系統的控制和狀態。其受到的控制和狀態約束條件為

umin≤uk≤umax，xmin≤xk≤xmax，k=1，…，∞

(3)

根據文獻[15]，可設計雙模預測控制規則使系統(2)在滿足約束條件(3)的同時具有穩定性保證。

首先定義性能指標函數

(4)

式中Q、R分別為狀態和控制的加權矩陣。

令雙模預測控制規則為

(5)

式中K為離線設計的無約束最優控制增益，一般采用LQR方法進行設計；ck(k=0，…，nc-1)為待優化的用于處理約束條件的自由變量。

將式(2)、式(5)代入式(4)中，得到[17]：J=cTWcc+p

(6)

其中

Wc=diag(W，…，E)

W=BTMB+R

M-ξTMξ=Q+KTRK

ξ=A-BK由于p與待設計的自由變量ck(k=0，…，nc-1)無關，可省略。

為便于描述基于多面體不變集的雙模預測控制方法，引入如下2個集合概念。

定義1[18](最大允許集合)：最大允許集合指該區域內狀態和控制及其預測值均滿足約束條件(3)。表示為

(7)

定義2[18](最大控制允許集合)：最大控制允許集合是指在控制規則(5)的作用下，控制和狀態及其未來時刻的預測值均滿足約束條件(3)。表示為

(8)

算法1[15](基于多面體不變集的雙模預測控制)

(1)離線計算式(5)中的無約束最優控制增益K；

(2)根據控制增益K和約束條件(3)，采用參考文獻[18]中算法3.2計算最大控制允許集合(8)；

(3)在每個采樣時刻，求解優化問題

(9)

取自由變量c中的第一個元素作為式(5)中的控制自由變量。若x∈S0，則c=0，無需進行優化求解。

2.2多參數二次規劃解的性質

考慮如下多參數二次規劃問題

(10)

文獻[16]采用KKT(Karush-Kuhn-Tucker)最優性條件已經證明：最優解z是關于參量x的分段仿射函數，即：z=kix(t)+gi，x(t)∈CRi，

其中，ki，gi，Xi，Yi可通過文獻[16]中的算法1求解得到。

定理1[16]：對于多參數規劃(10)，H>0，假設初始狀態所處的多面體集合X是凸集合，則在參數x的可行集合Xf內，最優解z是連續且是關于參量x的分段仿射函數。

2.3基于多參數規劃的離線雙模預測控制

雙模預測控制雖然通過離線求解控制增益K，在每一時刻只需求解優化問題(9)，減小了在線計算量。但是當系統的最大允許集合(8)包含較多約束時，仍然需要較多的在線計算時間。對于類似于高超聲速飛行器這樣的快動態系統不能滿足實時控制的要求。因此，本文根據多參數二次規劃解的性質，將雙模預測控制的在線優化問題看成一個多參數二次規劃問題，提出離線雙模預測控制方法。

對于優化問題(9)，把當前時刻狀態xk當作一個參量，則式(9)可看作一個多參數二次規劃問題。這樣可采用文獻[16]中的方法離線計算好雙模預測控制的自由控制變量及其對應的分區，這樣把自由變量的在線優化轉化為離線設計，在線時只需搜索當前時刻狀態所處的分區，極大減少了在線計算時間。

算法2(基于多參數二次規劃的離線雙模預測控制)

(1)離線計算無約束最優控制增益及其自由變量

選取合適的加權矩陣Q、R，采用LQR設計無約束最優控制增益K；把式(5)代入式(2)得到閉環系統

(11)

把式(11)表示為一個自治動態系統

(12)

其中

根據文獻[18]中算法3.2計算閉環系統(12)的最大控制多面體不變集Sc；根據多參數二次規劃解的性質，采用文獻[16]的算法1將多面體不變集Sc進行區域劃分并計算相應的自由變量系列f。

(2)在線搜索得到控制律

在線時，在多面體控制不變集內搜索當前時刻狀態所處的區域，得到相應區域的控制自由變量系列f，取第一個自由量ck，則當前時刻控制律為uk=Kxk+ck，ck=kixk+gi

3　高超聲速飛行器控制器設計及其仿真結果

3.1控制器設計

(1)建立預測模型

在預測控制中，需要建立控制對象的預測模型。為了便于問題求解，采用小擾動線性化模型作為高超聲速飛行器的預測模型。

在高超聲速飛行器的平衡狀態V0=4 590.3 m/s，h0=33 528 m，γ0=0°，q0=0(°)/s，α0=1.78 97°，β0=0.176 2，δe0=-0.39°， 進行小擾動線性化，得到

定義平衡點狀態x*=[V0γ0h0α0q0]T及控制u*=[β0δe0]T，將上述偏量系統的小擾動模型離散化得到預測模型，記為

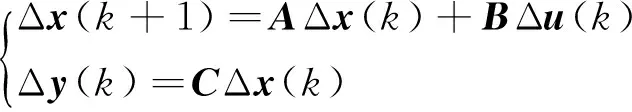
(13)

式中Δx=x-x*為偏量系統狀態；Δu=u-u*為偏量系統控制；Δy=y-y*為被控輸出。

(2)離線設計預測控制規則和最大控制允許集合

考慮控制和攻角的約束條件為

選取加權矩陣Q、R為合適維數的單位陣，選取自由狀態維數nc=2，根據算法2計算最大控制允許集合，將其投影到速度-高度平面，如圖1所示。將最大控制允許集合進行劃分并計算相應的控制自由變量，其區域劃分如圖2所示。

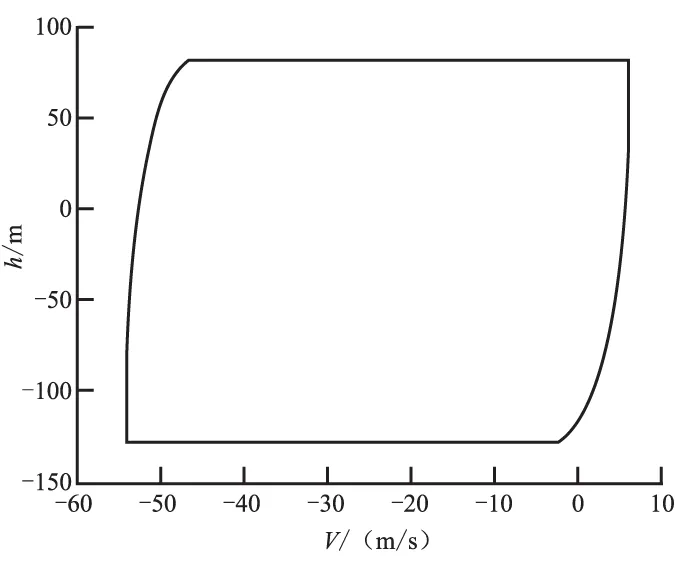
圖1　最大控制允許集合在速度-高度平面上的投影

(3)在線實施控制

在線時，在最大控制允許集合內搜索當前時刻狀態所處的區域，得到相應的控制自由變量ck。由于設計控制器時是對偏量系統(13)進行設計的，因此在實施控制規則時，應在控制中加上相應的平衡點才能施加到原來的非線性系統中，即作用到原系統的控制律為uk=-K(xk-x*)+ck+u*。

圖2　最大控制允許集合的狀態分區在速度-高度平面上的投影

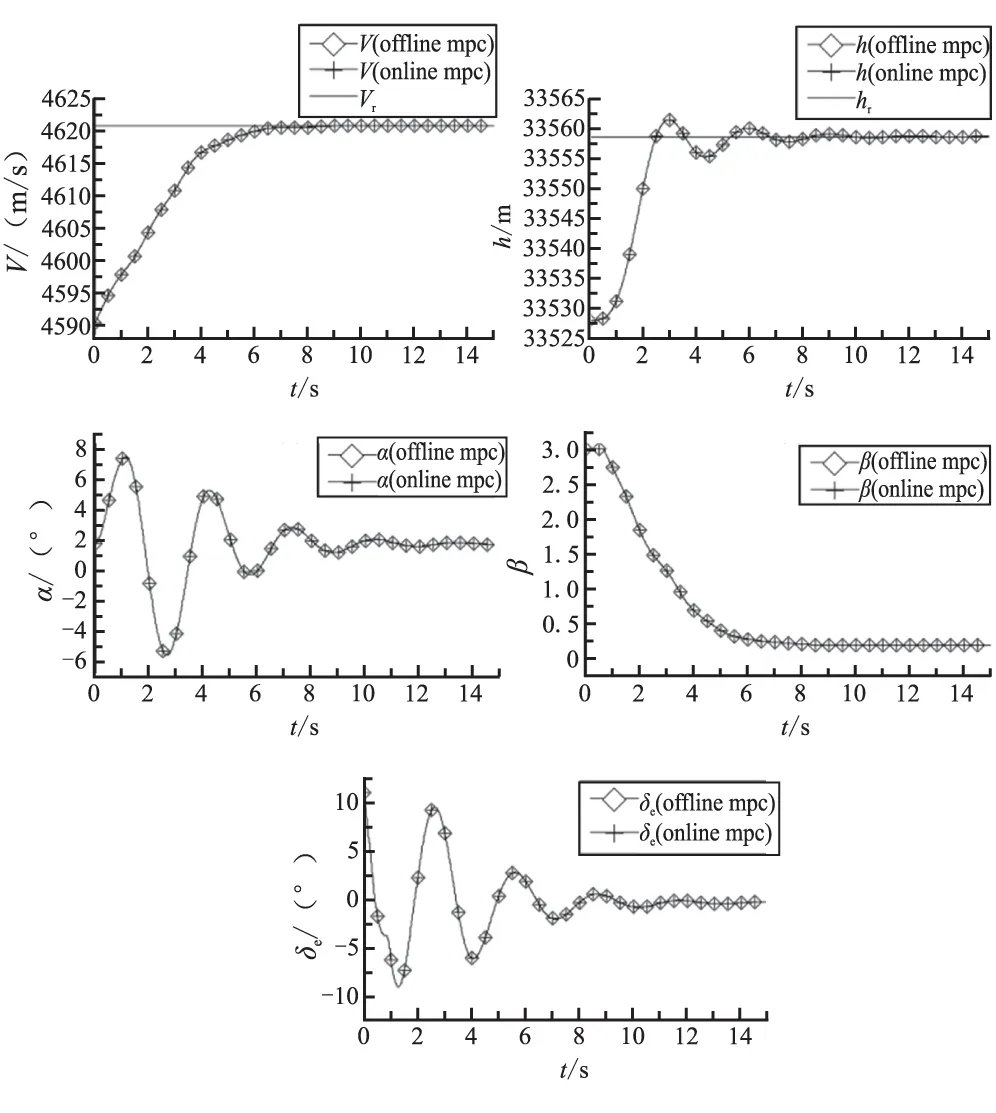
圖3　離線算法和在線算法的仿真結果對比圖

3.2仿真結果及分析

給定初始速度和高度分別為V0=4 590.3 m/s，h0=33 528 m，假定從0時刻起分別給定速度和高度參考階躍信號Vr=30.48 m/s，hr=30.48 m。用傳統基于多面體不變集的在線雙模預測控制方法和本文提出的離線雙模預測控制方法進行對比仿真，其仿真結果如圖3所示。圖中offline mpc表示采用本文提出的離線雙模預測控制方法，online mpc表示采用文獻[15]基于多面體不變集的在線雙模預測控制方法。

所采用的仿真環境為：硬件平臺為Intel(R) Pentium(R) Dual E2200@2.2 GHz 2.19 GHz、內存1.98 GB，軟件環境為Matlab2010b。在所進行的15 s仿真中，采用在線雙模預測控制方法仿真運行時間為：23.215 175 s，而采用本文提出的離線雙模預測控制方法仿真運行時間為：7.446 536 s。從圖3可看到，2種方法得到的速度、高度跟蹤曲線完全重合，均能實現速度和高度的參考指令信號跟蹤，且控制和攻角均在給定約束范圍內。這說明采用離線雙模預測控制方法在保持傳統雙模預測控制方法的控制性能的同時能實現高超聲速飛行器的實時控制。

4　結論

(1)提出一種適用于高超聲速飛行器的離線雙模預測控制方法。與傳統的雙模預測控制相比，此方法具有以下特點：繼承了基于多面體不變集的雙模預測控制方法的約束處理能力和良好控制性能；將傳統雙模預測控制的在線優化問題轉化成離線計算，在線時僅需要進行簡單的搜索，極大地減小了在線計算時間。

(2)仿真結果表明，所提出的方法在保持雙模預測控制的控制性能的同時，減少了在線運行時間，實現了對高超聲速飛行器的實時控制。

[1]Fidan B,Mirmirani M,Ioannou P A.Flight dynamics and control of air-breathing hypersonic vehicles:review and new directions [C]//12th AIAA International Space Planes and Hypersonic Systems and Technologies,Norfolk,Virginia,2003.

[2]孫未蒙,張靖男,張志強.高超聲速飛行器控制技術的幾個增長點[C]//中國航空學會控制與應用第十二屆學術年會論文集,2006:162-166.

[3]黃琳,段志生,楊劍影.近空間高超聲速飛行器對控制科學的挑戰[J].控制理論與應用,2011,28(10):1496-1505.

[4]Wang Q,Stengel R F.Robust nonlinear control of a hypersonic aircraft [J].Journal of Guidance,Control,and Dynamics,2000,23(4):577-585.

[5]Sigthorsson D O,Jankovsky P,Serrani A,et al.Robust linear output feedback control of an air-breathing hypersonic vehicle [J].Journal of Guidance,Control,and Dynamics,2008,31(4):1052-1066.

[6]Wilconx Z D,Mackunis W,Bhat S,et al.Lyapunov-based exponential tracking control of a hypersonic aircraft with aerothermoelastic effects [J].Journal of Guidance Control and Dynamics,2010,33(4):1213-1224.

[7]Fiorentini L,Serrani A,Bolender M A,et al.Nonlinear robust adaptive control of flexible air-breathing hypersonic vehicles [J].Journal of Guidance,Control,and Dynamics,2009,32(2):402-417.

[8]Xu H J,Mirmirani M D,Ioannou P A.Adaptive sliding mode control design for a hypersonic flight vehicle [J].Journal of Guidance Control and Dynamics,2004,27(5):829-838.

[9]Xu B,Sun F C,Yang C G,et al.Adaptive discrete-time controller design with neural network for hypersonic flight vehicle via back-stepping [J].International Journal of Control,2011,84(9):1543-1552.

[10]Li H Y,Wu L G,Gao H J,et al.Reference output tracking control for a flexible air-breathing hypersonic vehicle via output feedback [J].Optimal Control Applications and Methods,2011,33:461-487.

[11]Tao X Y,Hua C,Li N,et al.Robust model predictive controller design for a hypersonic flight vehicle [C]//2012 Proceedings of International Conference on Modelling,Identification and Control (ICMIC),NJ:IEEE,2012:1299-1304.

[12]Yang J,Zhao Z H,Li S H,et al.Composite predictive flight control for airbreathing hypersonic vehicle [J].International Journal of Control,2014,87(9):1970-1984.

[13]Cheng L,Jiang C S,Pu M.On-line-SVR-compensated nonlinear generalized predictive control for hypersonic vehicles [J].Science China-Information Sciences,2011,54(3):551-562.

[14]Kouvaritakis B,Rossiter J A,Schuurmans J.Efficient robust model predictive control [J].IEEE Transactions on Automatic Control.2000,45(8):1545-1549.

[15]Pluymers B,Rossiter J A,Suykens J,et al.A simple algorithm for robust MPC [C]//Proceedings of the IFAC World Congress,2005,Prague,Czech Republic.

[16]Bemporad A,Morari M,Dua V,et al.The explicit linear quadratic regulator for constrained systems [J].Automatica,2002,30(1):3-20.

[17]Rossiter J A.Model-based predictive control-a practical approach [M].Florida:CRC,2003:103-151.

[18]Gilbert E G,Tan T K.Linear systems with state and control constraints:the theory and application of maximal output admissible sets [J].IEEE Transactions on Automatic Control,1991,36(9):1008-1020.

(編輯：呂耀輝)

Off-line dual-mode predictive control method for hypersonic vehicle

GAO Hai-yan，CAI Yuan-li，MA Yu

(School of Electronic and Information Engineering,Xi’an Jiaotong University,Xi’an710049,China)

Considering the problem of the online computation time in the model predictive control for hypersonic vehicle,the off-line dual-mode predictive control was proposed.Firstly,the unconstrained control gain was designed by using the LQR(Liner quadratic regulor)method.Then the polyhedral invariant set was calculated according to the control gain and the constraints of the hypersonic vehicle.The polyhedral invariant set was divided based on the solution of the multi-parameter quadratic program,and the relevant free control variables were calculated simultaneously.On-line,the control law was obtained by searching the region of the current state,which reduces the online computation time noticeably.Simulation results show that the proposed method can not only maintain the control performance but also reduce the simulation time,and the real-time control for hypersonic vehicle can be attained.

hypersonic vehicle；dual-mode predictive control；multi-parameter quadratic program；polyhedral invariant set

2014-11-13；

2014-12-25。

國家自然科學基金(61202128，61308120，61463029)；中國博士后科學基金(2013M540783)。

高海燕(1986—)，女，博士生，研究方向為飛行器制導與控制。E-mail：g.a.o.haiyan@stu.xjtu.edu.cn

V448.12

A

1006-2793(2016)01-0120-05

10.7673/j.issn.1006-2793.2016.01.022