學會推理放飛思維

甘小生 李朝暉

推理是由一個或幾個已知的判斷（前提）推導出一個未知結論的思維過程，是數學的基本思維方式。教學中如何讓學生通過觀察、實驗、歸納、類比等思維方法獲得數學猜想，并進一步尋求證據、給出證明或舉出反例？又如何讓學生清晰、有條理地表達自己的思考過程并運用數學語言合乎邏輯地進行討論和質疑呢？

人教版《數學》六年級上冊《數學廣角——數與形》一課旨在引導學生在數與形之間建立聯系、發現規律，學會用數學語言清晰地表達思考過程。難點是讓學生經歷探索和驗證規律的過程，掌握數形結合、歸納推理的數學思想，增強觀察、歸納、類比、推理、探索規律的能力。筆者在教學中引導學生做了如下嘗試。

一、仔細觀察，發現異同，初見雛形

觀察是小學數學常用的一種學習方法，是一切發現的基礎。教學中教師要讓學生明確觀察的目的和方法，引導學生將觀察與思考相結合，并在此基礎上進行總結和歸納。

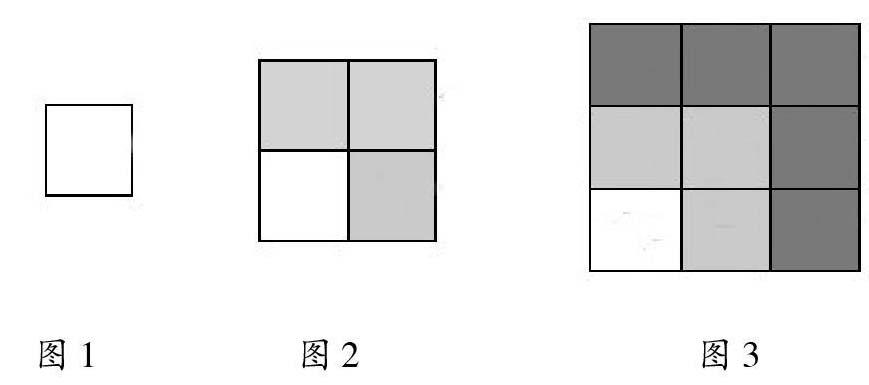
教學伊始，筆者出示圖1、圖2、圖3，讓學生仔細觀察并思考：三個圖形有什么相同或相似的地方？相鄰兩個圖形之間有怎樣的關聯？學生思考后發現：每個大圖形都是正方形；圖2中有4個像圖1那樣的小正方形，圖3中有9個；圖2比圖1增加了3個小正方形，圖3比圖2增加了5個小正方形……這樣依次下去，各個圖形中的小正方形個數分別是1，4，9……即1，1+3，1+3+5……；下一個圖形與上一個圖形相比，在外圍增加一個“L”形圖形。每個圖形里每行與每列中小正方形個數相同。那么，又該如何用算式表示每個圖形里小正方形的個數呢？學生的算法有兩種：第一種—— 1×1=12=1（圖1），2×2=22=4（圖2），3×3=32=9（圖3）；第二種—— 1=1=12（圖1），1+3=4=22（圖2），1+3+5=9=32（圖3）。那么每個圖形與相對應的算式又有什么關系？學生觀察后發現：算式左邊的加數是大正方形中右上角的小正方形和其它每一個“L”形圖形所包含的小正方形個數之和，算式右邊的數正好是每行或每列小正方形個數的平方。

以上教學中，筆者引導學生注意觀察圖形之間的相同或相似之處，觀察并思考圖形與數的對應關系。學生將嚴謹的數和直觀的形有機結合起來，既發現了數的特征，又發現了和的規律。

二、合理猜想，有效驗證，有序表述

建立在觀察、思考之上的合理猜想是探索數學規律和尋求數學本質的一種有效策略。驗證是為了證明猜想的合理性和正確性，常用方法有列舉、歸納、動手操作等。提出猜想、驗證猜想的過程中能充分發掘學生的探究意識和創新潛能。

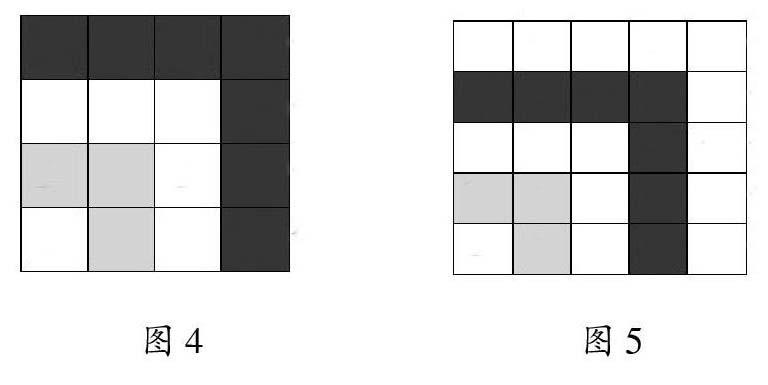
課中，筆者引導學生按照上面的發現提出自己的猜想，有學生提出：從1開始，幾個連續的奇數相加的和就是幾的平方。如何驗證這一猜想呢？筆者引導學生繼續思考“圖4” 可能是什么樣子？有幾個這樣的小正方形？怎么寫算式？“圖5”呢？學生思考后畫出了圖4、圖5，發現圖4中有16個小正方形，用算式表示是：1+3+5+7=42 ，圖5中有25個小正方形，用算式表示是：1+3+5+7+9=52。接著，筆者讓學生縱觀五幅圖及其對應的算式“1=12”“1+3=4=22 ”“1+3+5=9=32”“1+3+5+7=42”“1+3+5+7+9=52”并用簡潔的數學語言表述一下其中的規律。學生指出：第幾個圖形，加數就有幾個；加數個數是幾，和就是幾的平方；算式左邊是從1開始連續的奇數的和，右邊是一個數的平方。

以上教學中，筆者主要引導學生通過計算和動手畫圖兩種方法驗證猜想，并在驗證過程中，鼓勵學生有條理地表述，正確歸納出規律。

（作者單位：武漢市黃陂區長嶺小學）