基于PSO的6R裝配機器人手臂剛度優化

史旭東，莊立東，郭顯鵬

(1.南京工程學院 機械工程學院，南京 211167；2.江蘇理工學院 機械工程學院， 江蘇 常州 213000；3.康尼機電股份有限公司 技術中心，南京 210013)

?

基于PSO的6R裝配機器人手臂剛度優化

史旭東1，3，莊立東2，郭顯鵬3

(1.南京工程學院 機械工程學院，南京 211167；2.江蘇理工學院 機械工程學院， 江蘇 常州 213000；3.康尼機電股份有限公司 技術中心，南京 210013)

為了提高6R裝配機器人的末端定位精度，從提高其剛度性能出發，提出一種基于PSO的機器人臂長組優化算法。首先，在裝配機器人的靜剛度模型基礎上，提出末端剛度矩陣的“力-線位移矩陣”在手臂工作空間內奇異值的積分均值作為機器人末端剛度的定量評價指標，并以其為優化目標，建立機器人臂長組分配優化函數，研究利用PSO尋優算法對該優化函數求解；最后對某公司自主開發的KRT20-1540 裝配機器人，利用ANASYS仿真，驗證了該方法的可行性。

6R裝配機器人；工作臂；剛度優化

0 引言

自上世紀80年代起，隨著機器人工業化進程的推進，工業機器人以其高精度、高適應性，已從汽車領域被推廣到各行各業當中。6R裝配機器人即具有6個關節自由度的工業機器人，與一般的工業機器人相比，裝配機器人具有柔順性好、精度高、能配套使用等特點，是現代自動化裝配生產線不可或缺的一個重要單元[1-2]。

從傳統的機器人靜剛度模型分析可知，機器人末端剛度可通過機器人雅可比矩陣及關節剛度矩陣表述，而雅可比矩陣又與工業機器人的工作位姿和工作臂長密切關聯，因此若要提高工業機器人的剛度，一般常用的方法可采取提高關節剛度，如增加軸承、減速器、同步帶的剛度或者改變機器人的運動軌跡，尋找最佳的工作位姿和工作臂長以達到增加末端剛度的目的。由于軸承、減速器、同步帶的剛度影響因素基本是固定的，因此現階段國內外學者研究方向主要集中在研究機器人工作位姿與末端剛度的關系[3],而從臂長優化角度研究機器人的剛度目前還不多。本文從優化裝配機器人的工作臂長分配來考慮，利用PSO尋優算法，提出一種新的6R工業裝配機器人臂長優化方法。

1 6R裝配機器人剛度定量分析模型

1.1 工作臂靜剛度模型

本文以某公司自主研發的20KG級工業裝配機器人(KRT20-1540)為優化對象,其結構如圖1主要包括腰部、肘部、大臂、小臂及末端執行器等幾個部件，其中大臂和小臂是承載工作負載及轉矩的主要柔性連桿，大臂和小臂的剛度性能直接關系到機器人末端的定位精度。

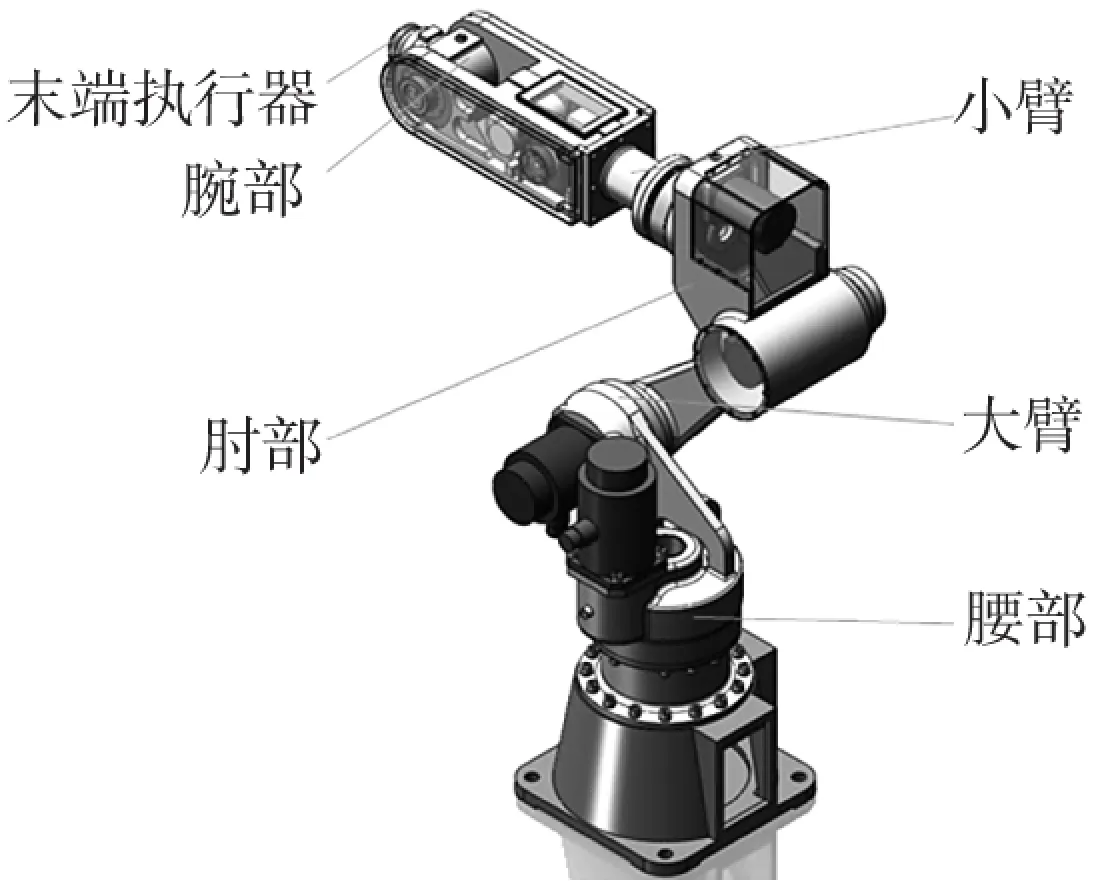
圖1 KRT20-1540 結構模型

依據D-H方法建立機器人連桿坐標系，如圖2，并確定建立裝配機器人齊次坐標矩陣的各關節連桿參數如表1所示。

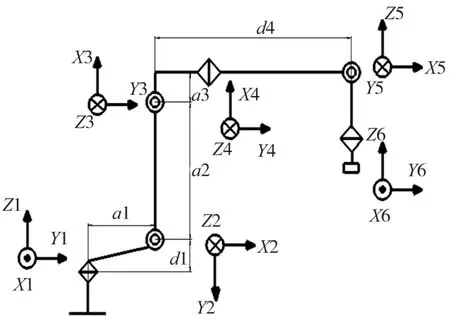
圖2 KRT20-1540連桿坐標系

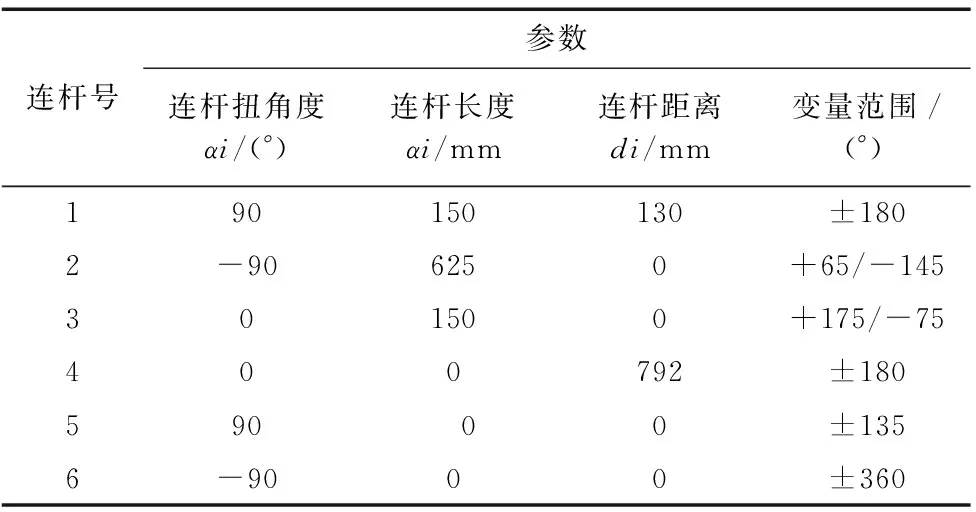
連桿號參數連桿扭角度αi/(°)連桿長度αi/mm連桿距離di/mm變量范圍/(°)190150130±1802-906250+65/-145301500+175/-75400792±180590 00±1356-9000±360

由于雅可比矩陣描述的是手臂線位移與角位移的映射關系，即

dx= J·dθ

(1)

式中： dx—關節微小線位移 ；

dθ—關節微小角位移。

根據表1中所列D-H連桿參數，利用微分變換的方法即可求得裝配機器人的雅可比矩陣 J[4]。

為了求解裝配機器人的靜剛度模型，還需對裝配機器人各關節剛度Kti(i表示所對應的關節序號)進行分析，求得其關節剛度矩陣Kt，則

Kt=diag(Kt1，Kt2，…，Kt6)

(2)

由于裝配機器人各關節剛度為定值，可根據裝配機器人傳動結構及各主要零部件的扭轉剛度的經驗公式進行推導，Kt與電機扭轉剛度kd和齒輪扭轉剛度有關，其中：

(1)電機的扭轉剛度為[5]：

kd= 4π2t2·J

(3)

式中：t為機械時間常數；J為電機轉子的轉動慣量。

(2)齒輪的扭轉剛度計算[6]：

kc=Cgbr2

(4)

式中：b為齒寬；r為齒輪半徑；對鋼材Cg=1.34×1010 N/m2

裝配機器人末端剛度矩陣Q為：

Q=J-T KtJ-1

(5)

此即該裝配機器人的靜剛度模型[7]。由式(2)可知，裝配機器人的末端剛度與關節剛度矩陣和雅可比矩陣有關，而關節剛度為定值，則最終影響到機器人末端剛度的主要因素為裝配機器人雅可比矩陣。由前式(1)分析，雅可比矩陣 J描述的是機器人工作臂線位移和角位移的映射關系，線位移和角位移又與裝配機器人的工作位姿和工作臂長密切相關，因此本文著重研究的是KRT20-1540裝配機器人工作臂空間運動中臂長的最優解。

1.2 機器人末端剛度定量分析

上文分析了裝配機器人的靜剛度模型，但由于靜剛度模型只能定性的描述裝配機器人末端剛度的影響因素，并不能對裝配機器人末端剛度進行直觀的評價，為此還需提出一種對裝配機器人剛度定量評價的方法。

可將裝配機器人抵抗外力變形的能力定義為該裝配機器人的末端剛度。按照胡克定律，則裝配機器人空間受力F和變形D表示為：

F=Q·D

(6)

而按照量綱的不同，可將靜剛度矩陣Q劃分為4塊，即：

Q=KfdKndKfqKnq

(7)

其中： Kfd為力-線位移矩陣；Knd為力矩-線位移矩陣；Kfq為力-角位移矩陣；Knq為力矩-角位移矩陣。

為此可將式(6)分解為：

dq=KfdKndKfqKnqfn

(8)

式中：f為末端力矢量；n為末端力矩矢量；d為末端線位移；q為末端角位移。

考慮到裝配機器人在裝配作業中定位及壓緊的受力方式，可從力-線位移剛度矩陣角度來衡量機器人的末端剛度。由文獻[8]，可選“力-線剛度橢球 ”最小半軸長即 Kfd的最小奇異值ξ作為衡量裝配機器人剛度性能的指標，ξ值越大，則相應的裝配機器人剛度性能越好，然而根據雅可比矩陣的特性，ξ只能描述裝配機器人在某特定工作位姿下的剛度性能，因此還需進一步分析其綜合剛度 Σζ，參照文獻[9]，對Kfd的奇異值ξ在整個機器人工作空間內進行積分并求出其平均值Σζ，即：

(9)

式中：W為機器人可達空間；φ為機器人關節空間；θi為機器人關節角(i=1、2、3，…，n)。

因此，最終可用 Σζ 來描述裝配機器人整體剛度性能的好壞， Σζ 越大，則末端剛度越大，優化模型以求解 Σζ的最大值建立目標優化函數。

2 剛度優化

2.1 優化模型的建立

對于本次設計優化的6R裝配機器人，由于機器人后3個自由度主要集中在小臂旋轉及腕部定位，其對機器人整體的空間剛度影響較小，因而可將該機器人的剛度問題進行簡化處理，分析裝配機器人大臂、小臂在滿足工作半徑前提下的最優臂長分配。此時問題就轉換為單目標多元函數在既定約束條件下最優解的數學問題。該優化模型可描述為：

maxΣζ st.Limin ≤Li≤LimaxL1+L2+…+Ln=L

(10)

2.2 PSO粒子群優化算法

粒子群優化算法(Particle Swarm Optimization,PSO)是1995年由艾伯哈特(Eberhart)和肯尼迪(kennedy)2位學者通過研究鳥群捕食行為所提出的一種新的進化算法。PSO算法的基本原理是利用群體中的個體對信息的共享使整個群體的運動在問題求解空間中產生從無序到有序的演化過程，從而獲得最優解，但與遺傳算法相比，其迭代公式更加簡單，且具有高魯棒性、高收斂速度的優點，使其在工業設計中展現出非常高的應用價值，并得到學術界的廣泛重視[10]。

對本文6R裝配機器人手臂剛度優化設計，定義手臂Li(i=1、2、3…n)的解為空間搜索粒子，這群隨機搜索粒子在空間中按速度v進行隨機飛行搜索，在搜索過程中不斷比較粒子當前位置與本身最好位置以及整個粒子群中所發現的最后位置，并根據式(10)中確定的適應度值f以及利用式(11)進行迭代計算：

vik+1=ωvik+c1 μ pik-xik+c2 η[ pgk-xik]

xik+1= xik+vik

(11)

其中：ω為慣性權重；c1 、c2為粒子學習因子；μ、η為在[0,1]之間的均勻分布的偽隨機數； xi為粒子當前位置； vi為該粒子當前速度；pi為該粒子最好位置； pg為群體內所有粒子最好位置。經過迭代，最終可求出裝配機器人Li的最優解組合。

3 應用實例

3.1 機器人關節剛度計算

本次KRT20-1540裝配機器人主要從優化機器人工作臂長的角度來提高其末端剛度，為了方便計算，將后3個自由度簡化，與小臂扭轉關節合并，其傳動鏈及傳動原理如下表2和圖3所示。

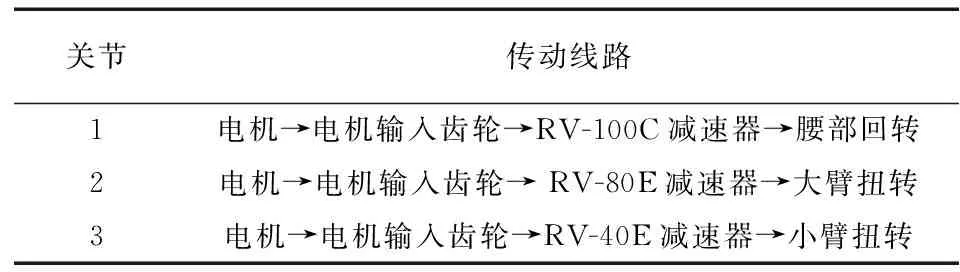
表2 各關節的傳動路線

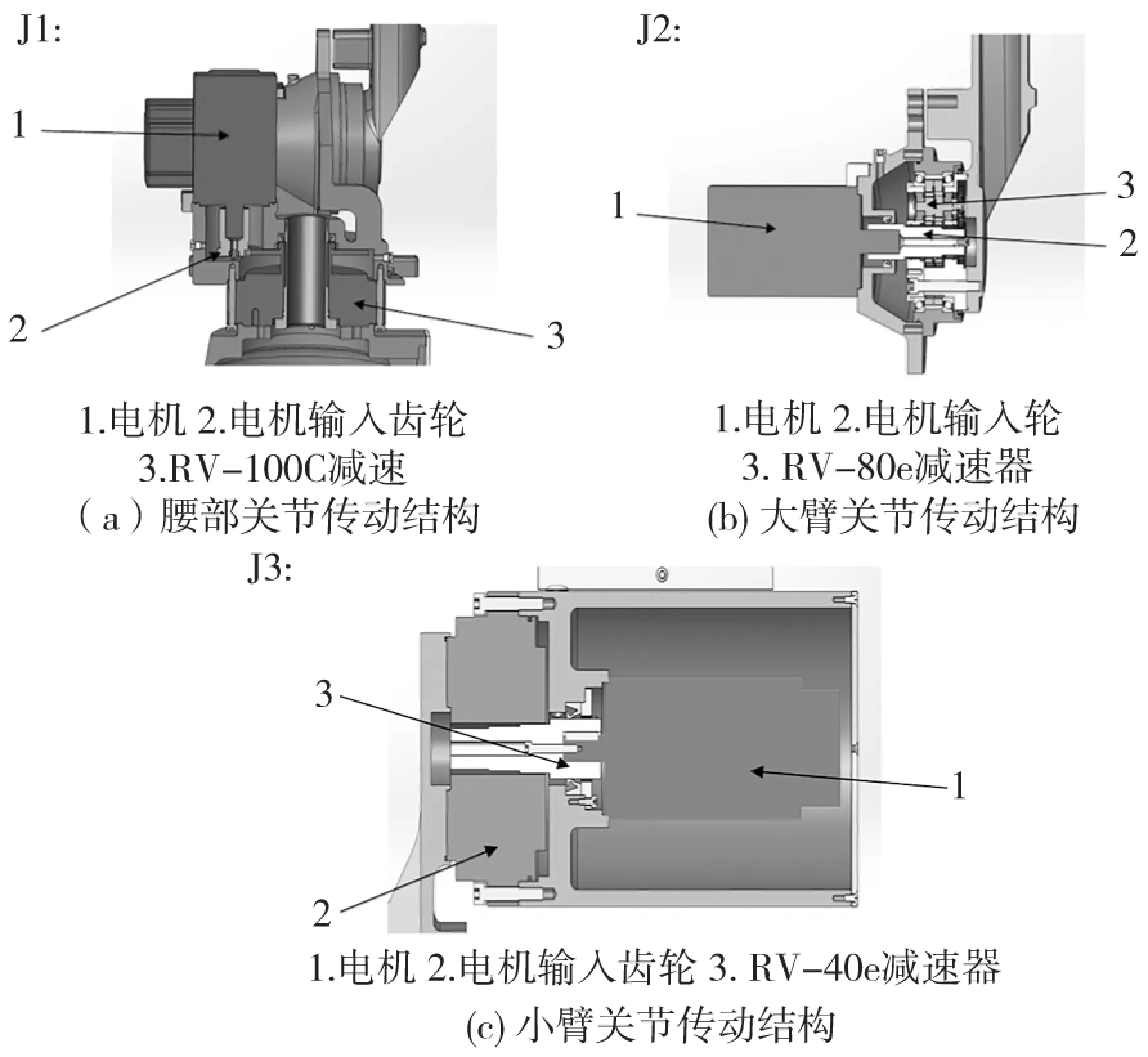
圖3 傳動關節結構圖

J1腰部回轉關節選用的是日本山洋R2AA13200DCPW0交流伺服電機，該電機的扭轉剛度kd可按式計算，從山洋伺服電機樣本中可查得t=0.83 ms，J=12.2×104N·mm ，由式(3)最終得電機扭轉剛度kd1=5.81×108N·mm/rad ；電機輸入齒輪的齒寬b=20mm，齒寬半徑r=18mm ，由式(4)可得其扭轉剛度kc1=8.68×104N·mm/rad；J1關節中減速器選用的是日本帝人RV-100C-36，該減速器的扭轉剛度kr可從帝人減速器樣本中查得，kr1=3.06×107N·mm/rad

為了計算J1關節的總剛度，還需把傳動系統中各機械部件的剛度一一折算到輸出軸上，計算等效剛度。在此，為了簡化計算，可將傳動系統各部件簡化成由幾個彈性部件串聯組成的系統，并按折算前后系統動能或勢能保持不變的原則進行折算。折算后電機等效剛度kd1′=kd1·i2，齒輪等效剛度為kc1′=kc1·i2 ，RV減速器的等效剛度為kr1′=kr1，其中i為RV減速器的減速比，則J1關節綜合扭轉剛度k1為:

1k1=1kd1′+1kc1′+1kr1′

(12)

最終計算得腰部回轉關節扭轉剛度k1=7.06×107 N·mm/rad，同樣的方法可求得k2= 6.23×108N·mm/rad；k3=3.12×107 N·mm/rad ；Kt=diag(7.06×107， 6.23×108，7.23×107)

3.2 機器人臂長優化

根據上文的分析，KRT20-1540裝配機器人在對工作臂進行優化設計時為了方便計算，將后3個自由度簡化，故其雅克比矩陣Jk較傳統6R機器人有所不同，可令:

Jk=[ J1， J2 ，J3，J4]

(13)

其中 ：

J1=d4s23-a2c2-a3c23a2c1+a3c13-

d4s23a2c2-a3c23-d4s231

J2=a3c6 -d4c4-a2a3 -d4c4+a2a2-a3-d41

J3=d4+a3d4-a3d4c4+a20

J4= 0001

式中：c1=cosθ1，s1=sinθ1，s23=sin(θ2+θ3)并依此類推，將表1中KRT20-1540裝配機器人的D-H連桿參數帶入，結合式(5)、 (8)最終可解得本機器人“力-線位移矩陣”

Kfd=-L1sinθ2-L2sin(θ2+θ3-L2sin(θ2+θ300L1cos(θ2)+

L2cos((θ2+θ3)L2cos((θ2+θ3)0000-101101

(14)

式中：L1為大臂臂長；L2為小臂臂長；θ2、θ3為大臂、小臂工作轉角。由于受到工作范圍的限制，故大臂、小臂關節角的約束條件設定為θ2∈[ 1.13，-2.53 ]，θ3∈[ 3.05，-1.31](單位弧度)，同時還需保證KRT20-1540裝配機器人的最大工作半徑為1540，故該優化模型可表示為：

maxΣζ (L1，L2)st.θ2∈ [ 1.13，-2.53 ]

θ3∈[ 3.05，-1.31 ]L1+L2=1540

(15)

該優化問題可利用PSO粒子群算法求解。在此借助Matlab粒子群工具箱(PSOt)，并指定慣性因子、約定各維變量的取值范圍等即可，其具體的調用函數為：

pso_Trelea_vectorized(functname, D, mv, VarRange , minmax, PSOparams, plotfcn, PSOseedValue)

其中，對于本次優化問題，其調用函數為:

test_func = max Σζ (L1，L2)

L1_range=[-2,2]；

L2_range=[-2,2]；

range=[L1_range; L2_range]；

Max_V=0.2* (range(:,2) - range(:,1))；(最大速度取范圍的 10%～ 20%)

n=2(粒子維數 )

PSOparams = [10 1000 50 2 2 0.9 0.4 1500 1e-25 250 NaN 0 0] (個體數目 50 ，進化次數1000)

PSO_Trelea_vectorized('test_func',n, Max_V, range, 1, PSOparams)

最終解得最優臂長解為L1*= 625.6， L2*= 792.8,具體設計時取整L1*= 626，L2*=793。

3.3 優化結果驗證

本次優化設計的裝配機器人KRT20-1540，其負載為20kg，在ANASYS仿真軟件中將其模型簡化并在末端施加200N的作用力，規定好約束并對整個模型網格劃分后進行應力應變分析；同時給出另外2組臂桿長度在相同位姿下與優化臂長組對比其應力應變量，仿真結果如圖4。

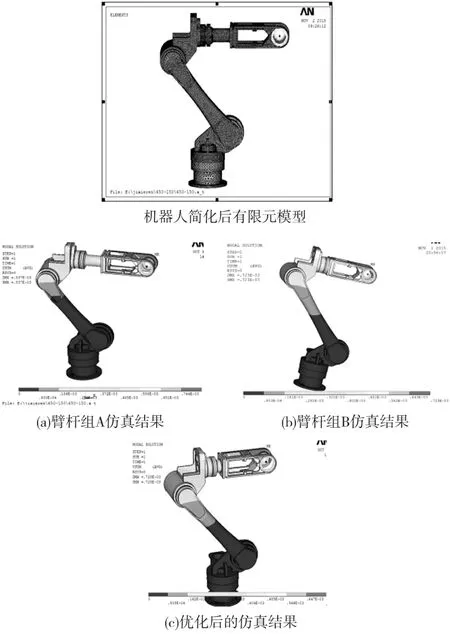
圖4 臂桿優化仿真對比

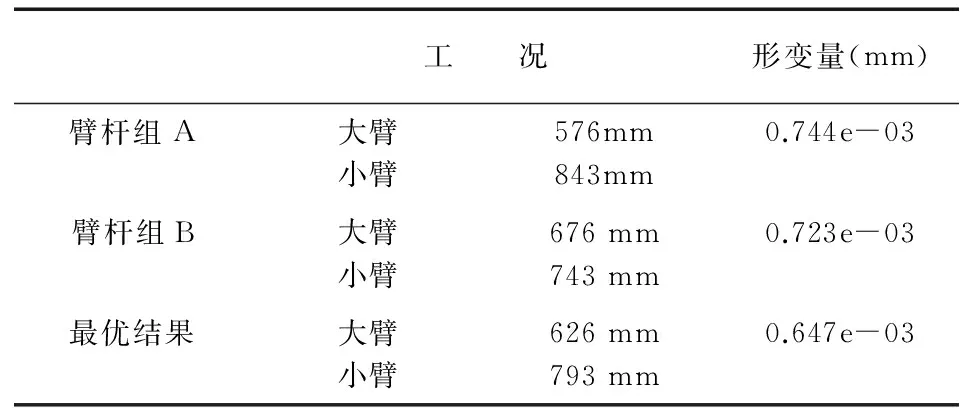
工 況形變量(mm)臂桿組A大臂小臂576mm843mm0.744e-03臂桿組B大臂小臂676mm743mm0.723e-03最優結果大臂小臂626mm793mm0.647e-03

由上表4仿真結果可知，該優化方法是切實可行的。

4 結束語

本文以某公司自主研發的6R裝配機器人為例，研究分析了其剛度模型，并提出了基于PSO的機器人工作臂長組優化，為提高機器人末端剛度提出了一種新的思路。

本文靜剛度模型中以“力-線位移矩陣”奇異值在工作空間內的積分均值作為定量分析指標，簡化分析了后3個自由度對剛度的影響，后期考慮到優化模型的精確性，在計算剛度模型時可將其帶入計算；同時，機器人的工作位姿也是決定末端剛度性能的一個重要影響因素，空間積分均值并不能完全表達，因此有必要進一步探討位姿與工作臂長相結合的剛度優化方法，對提高機器人精度具有更加重大的意義。

[1] 駱敏舟,方健,趙江海. 工業機器人的技術發展及其應用[J]. 機械制造與自動化，2015(10):1-4.

[2] 董欣勝,張傳思,李新. 裝配機器人的現狀與發展趨勢[J]. 組合機床與自動化技術，2007(8):1-4.

[3] Wang M X. 機器人技術基礎[M]. 武漢:華中科技大學出版社，1996.

[4] 聞邦椿. 機械設計手冊 [M]. 北京:機械工業出版社，2010.

[5] 林義忠,廖小平,曾劍. 6R噴涂機器人操作臂末端剛度分析 [J]. 廣西大學學報：自然科學版，2011，36(2)：234-240.

[6] John J Cring.機器人學導論[M].贠超,譯.北京：機械工業出版社，2012.

[7] Abele E,Weigold M ,Rothenbucher S. Modeling and indentification of a industrial robot for machining application. Annals of the CIRP，2007,56(1)：387-390.

[8] 曲巍崴，侯鵬輝，楊根軍.機器人加工系統剛度性能優化研究[J].航空學報,2013,34(12):2823-2823.

[9] Gosselin C，Angeles J.A global performance index for the kinematic optimization of robotic mainpulators[J].ASME Journal of Mechanical Design，1991,11(3)：220-260.

[10] Blum C, Merkle D.群智能(精)[M]. 龍飛,譯.北京：國防工業出版社，2011.

(編輯 李秀敏)

Arm Stiffness Optimization of a 6-DOF Assembly Robot Based on PSO

SHI Xu-dong1，3，ZHUANG Li-dong2，GUO Xian-peng3

(1.School of Mechanical Engineering,Nanjing Institute of Technology,Nanjing 211167,China; 2.School of Mechanical Engineering, Jiangsu Institute of Technology，Changzhou Jiangsu 213000,China)

To increase the repeat location accuracy of a 6-dof assembly robot , a method of optimization of its link length is proposed based on PSO through improving the stiffness performance. The integral mean value of singular-value of force-displacement matrix on link work space is used as the quantitative index to measure the link stiffness. With the aim of its optimization, the optimization function of link length is set up and solved based on PSO. Finally, on the company independently developed KRT20-1540 assembly robot, the feasibility of the method is verified through ANASYS simulation.

6-dof assembly robot;link length; stiffness optimization

1001-2265(2016)10-0043-04

10.13462/j.cnki.mmtamt.2016.10.011

2015-11-10；

2015-12-15

史旭東(1968—)，男，江蘇溧陽人，南京工程學院高級工程師，研究方向為機械加工工藝與自動化設備，(E-mail)shixudong@live.cn。

TH166;TG659

A