6-DOF焊接機器人的路徑優化算法研究

◎盧佳佳

（阜陽職業技術學院工程科技學院 ，安徽 阜陽 236031）

6-DOF焊接機器人的路徑優化算法研究

◎盧佳佳

（阜陽職業技術學院工程科技學院 ，安徽 阜陽 236031）

以六自由工業機器人為對象，研究機器人焊接作業時的路徑優化算法。對六自由工業機器人的逆運動學原理進行介紹，分析在一定范圍內的焊接作業路徑優化，以時間最短或路徑距離最短為研究指標，選擇兩種智能算法（遺傳算法和Hopfield神經網絡算法）進行分析。運用MATLAB軟件進行仿真測試，對比分析它們的優缺點，為下一步焊接機器人的路徑優化實驗奠定基礎。

焊接機器人；遺傳算法；Hopfield神經網絡；路徑尋優

隨著焊接機器人的廣泛使用，針對機器人工作效率和能耗使用的研究越來越深入，如何為焊槍頭計算出合適的運動路線，使其沿著規劃出的最優路線完成焊接任務成為關鍵問題。機器人在限定的空間范圍內使末端焊鉗（焊槍）從一個位姿移動到另一個位姿，同時要滿足速度、加速度、加加速度和力矩等約束的限制，以時間最短或路徑距離最短為研究指標，進行焊接次序的規劃[1-3]。

該文分別對兩種比較常見的路徑尋優智能算法，即遺傳算法和神經網絡算法進行研究，并使用MATLAB軟件進行模擬仿真，通過對比分析兩種算法的優缺點，為下一步實驗室的六自由度工業機器人路徑優化實驗提供理論基礎。

1　基于遺傳算法的路徑尋優設計

針對焊接機器人的路徑尋優，以焊接先后次序作為遺傳算法的編碼，將走過焊點的路徑長度作為目標函數。考慮路徑尋優問題的各種約束條件，設定合理的參數初始值，保證所有的焊接點都走過一遍。具體優化步驟如下[4]。

第一步：參數編碼和初始群體設定。設焊點總數為N，則編碼形式采用N進制，即每個個體的長度為N，個體中的每個基因只取1到N中的一個整數。設樣本中有s個個體，則群體可以用一個s行t列的pop矩陣來表示，其中t=N+1。

第二步：計算路徑長度的函數設計。在焊點路徑尋優規劃中，用路徑總長作為適應度函數，來衡量計算的結果是否最優。將pop矩陣中每一行的第N+1個元素作為路徑長度，則焊點m和焊點n之間的距離可用下式計算：

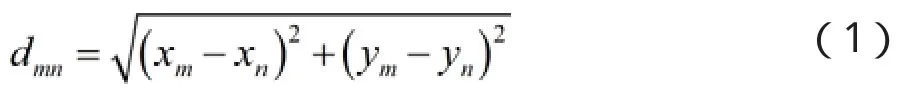
目標函數可以通過樣本的路徑總長得出。根據t的定義，兩兩焊點的組合數共有t-2組，則目標函數為：

自適應度函數為目標函數的倒數，即

第三步：選擇算子的計算。選擇操作體現的是一個優勝劣汰的過程，其以群體中個體的適應度強弱作為評判條件，能夠將群體中適應度最強的c個個體直接替換掉適應度最弱的c個個體。

第四步：交叉算子的計算。設定一個交叉概率Pc，判斷系統當前隨機值，若隨機值大于交叉概率Pc，則從群體中隨機選擇兩個個體進行交叉配對，將配對的個體通過替換重組而生成新的個體。

第五步：變異算子的計算。同樣設定一個變異概率Pm，判斷系統當前隨機值，若隨機值大于交叉概率Pm，則采用倒置變異法對群體中個體串某些基因位上的基因值作變動，判斷變動后子代個體的適應度值是否優于父代，若優于父代則保留新的染色體，否則仍保留原染色體。

2　基于Hopfield神經網絡的路徑尋優設計

Hopfield神經網絡模型是由一系列互連的神經元組成的單層反饋系統，結構模型如圖1所示。

圖1　Hopfield神經網絡模型圖

圖中虛線框內的結構表示第i個神經元，ui為狀態輸入，vi為神經元的輸出，是關于輸入變量ui的一個非線性函數。神經元中Ri和Ci分別為輸入電阻和輸入電容，Ii為輸入電流，Wij看作第j個神經元到第i神經元的連接權值。

對于Hopfield神經網絡第i個神經元，采用微分方程建立其輸入、輸出關系，即：

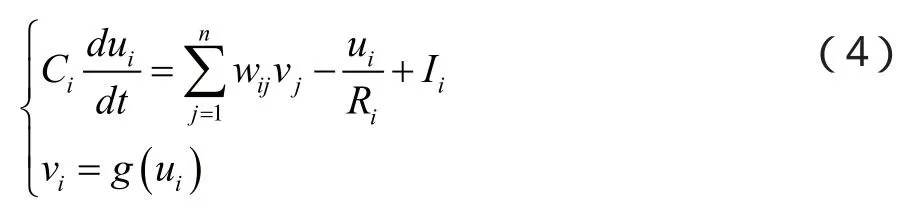
式中，i=1，2，……，n。

其中，g（·）為雙曲函數，一般取為：

式中，ρ＞0，λ＞0。

u=（u1，u2，……，un）T為n個神經元的網絡狀態向量；V=（V1，V2，……，Vn）T為網絡的輸出向量；I=（I1，I2，……，In）T為網絡的輸入向量。

將Hopfield網絡的標準能量函數定義為

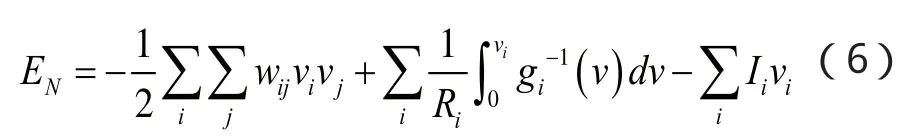
當W為對稱的權值矩陣時（即Wij=Wji），則[5]

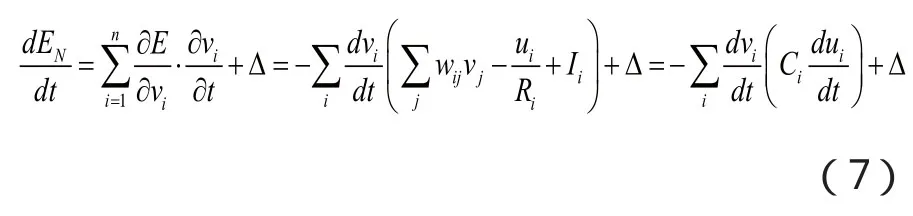
?為很小實數。

由于vi=g（ui），則

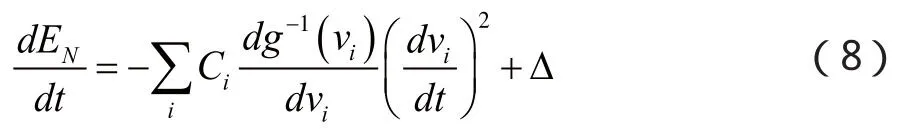
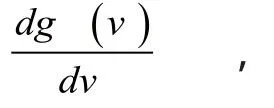
可以看出，隨著迭代次數的增加，能量函數EN逐漸減小直至穩定，最終系統達到穩定平衡點，此時網絡輸出的向量V即是EN的極小點。

3　路徑尋優仿真與分析

設D={dij}是由焊點i和焊點j之間的距離組成的距離矩陣，機器人路徑尋優就是求出一條通過所有焊點且每個焊點只通過一次的具有最短距離的回路。建立大地坐標系，使Z軸恒等于0，即所有的焊點都在同一個水平面上，隨機抽取10個焊點如表1，分別采用遺傳算法和Hopfield神經網絡算法進行路徑尋優仿真[6-8]。

表1　10個焊點坐標表

3.1采用遺傳算法仿真

采用遺傳算法對10個焊點進行路徑尋優時，通過調試設定交叉概率Pc=0.10，變異概率Pm=0.80，群體中個體數目s=40，c=20。通過改變進化代數k，觀察不同進化代數下路徑的優化情況。

經過100次進化，焊點組合路徑能夠達到最小。最短路徑為3.591 9，如圖2所示。通過仿真分析，在進行100次路徑尋優的仿真實驗中，有83次能夠得到最優解，也就是說系統每次計算時約有83%的概率算出最優路徑。

圖2　10個焊點進化100次時的優化效果對比圖

3.2 采用Hopfield神經網絡算法仿真

采用Hopfield神經網絡算法進行路徑尋優求解時，將能量函數定義為[9]

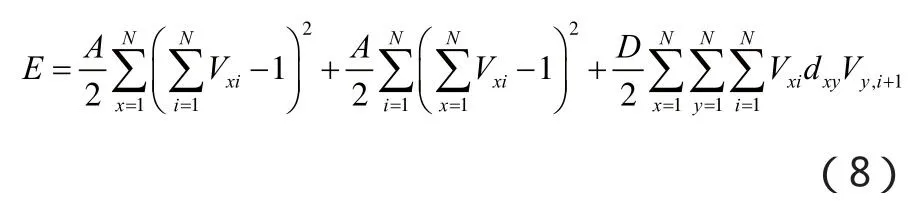
式中，取A=1.5，D=1.0。

對10個焊點進行路徑尋優，如果初始化的尋優路徑有效，即路徑矩陣中各行各列只有一個元素為1，其余為0，則給出最后的優化路徑，否則停止優化，需要重新運行優化程序。置處置A=1.5，D=1.0，離散時間?T=0.01，若本次尋優路徑有效，經過1 500次迭代，初始路程為4.394 1，最短路程為3.591 9，如圖3所示；最優能量函數為E=1.647 1，如圖4所示。

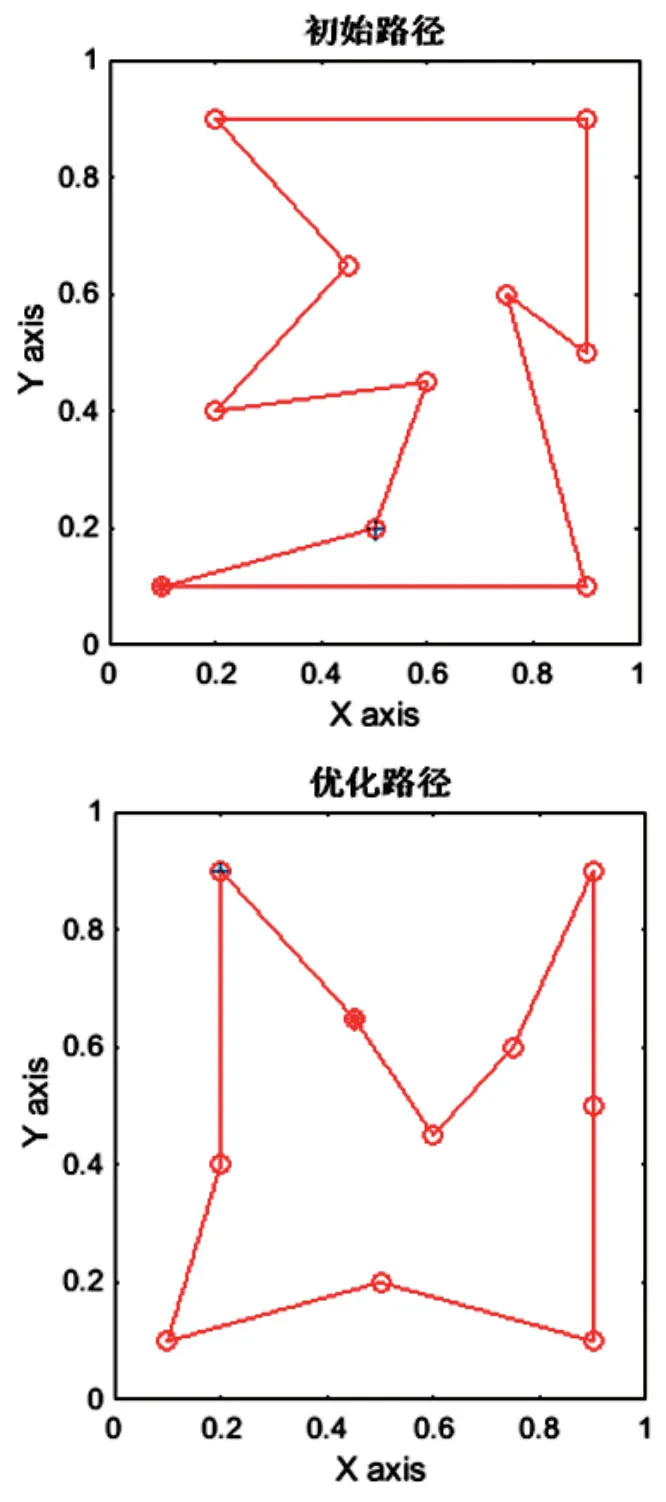
圖3　10個焊點的初始路徑和優化路徑對比圖

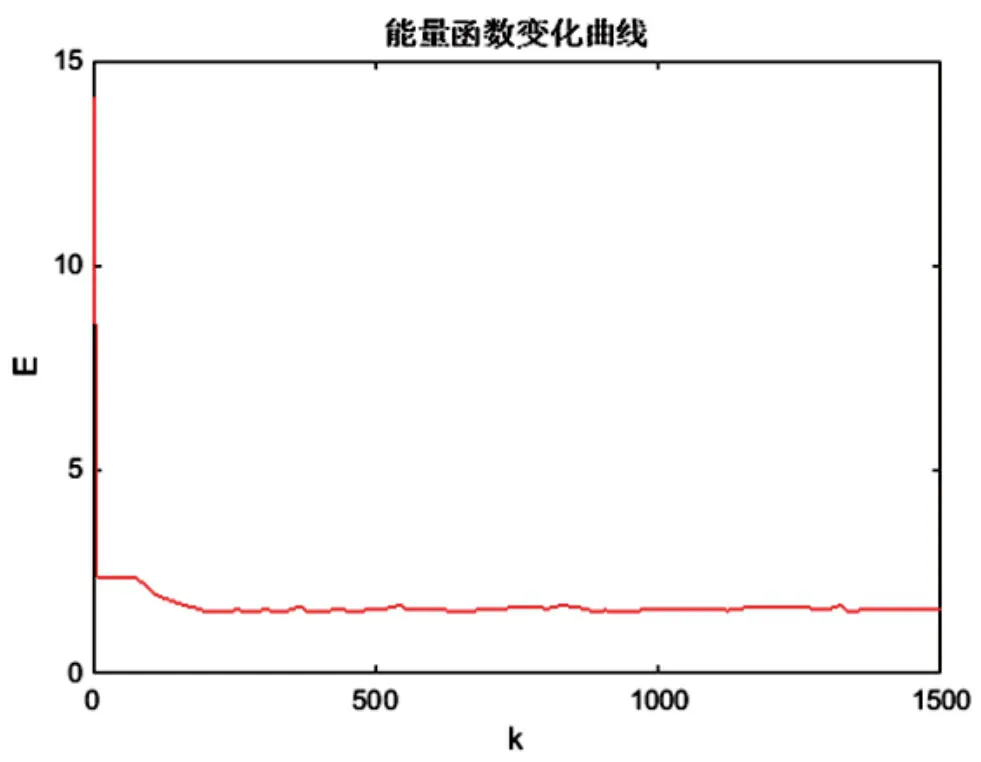
圖4　能量函數隨迭代次數的變化曲線圖

4　結論

（1）在對10個焊點進行模擬路徑優化時，選擇合適的交叉概率和變異概率參數，從仿真試驗結果可以看出，經過100次進化，即可計算出焊接機器人的最短焊接路徑，從而體現出了遺傳算法在路徑優化時全局搜索的特點。

（2）Hopfield網絡是一種反饋型神經網絡，其具有一個重要特征就是能夠達到穩定狀態，從仿真試驗結果可以看出，當網絡達到穩定狀態時（即算出最短路程為3.591 9），能力函數達到最小（即最優能量函數E=1.647 1）。

（3）兩種優化算法各有利弊，在仿真測試中發現，初始值的設定尤為重要，會直接影響到試驗效果。因此針對實際情況，要不斷調試仿真，找出最佳參數，才有可能應用于下一步的機器人試驗中。

基于以上分析，下一步的研究工作是比較選擇出一種更適合實際運用的優化算法，應用到實驗室的RBT-6T型工業機器人上，并嘗試與視覺圖像實時采集相結合，實時根據焊點分布計算出最優路徑。

[1]Saeed B.Niku.機器人學導論—分析、控制及應用（第2版）[M].北京：電子工業出版社，2013.

[2]蘭 虎.工業機器人技術及應用[M].北京：機械工業出版社，2014.

[3]王田苗，陶 永.我國工業機器人技術現狀與產業化發展戰略[J].機械工程學報，2014，50（9）：1-13.

[4]劉金琨.智能控制（第3版）[M].北京：電子工業出版社，2014.

[5]J J Hopfield，D W Tank. Neural computation of dicision in optimization problems[J]. Biological Cybernetics，1985，7（52）：141-152.

[6]徐海黎，解祥榮，莊 健，等.工業機器人的最優時間與最優能量軌跡規劃[J].機械工程學報，2010，46（9）：19-25.

[7]苗建偉.一種六自由度機械手的智能軌跡規劃[D].成都：西南交通大學，2014.

[8]王 寧，張新敏.基于MATLAB的六自由度機器人軌跡規劃與仿真[J].制造業自動化，2014，36（8）：95-97.

[9]孫守宇，鄭君里.Hopfield網絡求解TSP的一種改進算法和理論證明[J].電子學報，1995，23（1）：73-78.

Algorithm Research of 6-DOF Welding Robot Path Optimization

Lu Jiajia

（Department of Engineering Science and Technology College， Fuyang Vocational Technical College，Fuyang 236031， China）

Based on six free industrial robots， the path optimization algorithm for robot welding was studied. The principle of inverse kinematics of six free industrial robots was introduced； the path optimization of welding operation in a certain range was analyzed， in the shortest time or shortest distance path index， this paper choose between two intelligent algorithms （genetic algorithm and Hopfield neural network algorithm） for analysis. Using MATLAB software simulation testing， their strengths and weaknesses were compared， in order to lay the foundation for the next step welding robot path optimization experiment.

Welding robots； GA； Hopfield neural network； Route optimization

TP242

10.16736/j.cnki.cn41-1434/ts.2016.08.020

基于ANN的焊接機器人路徑規劃研究——以我校六自由度工業機器人為對象（編號：KJ2016A561）。

盧佳佳（1987-），男，安徽阜陽人，碩士研究生，助教；主要研究方向為機器人智能控制。