四自由度行星變速機構方案性能規律研究

李慎龍， 毛明， 蓋江濤， 劉樹成

(1.北京理工大學 北京電動車輛協同創新中心， 北京 100081;2.中國北方車輛研究所 車輛傳動重點實驗室， 北京 100072)

?

四自由度行星變速機構方案性能規律研究

李慎龍1,2， 毛明2， 蓋江濤2， 劉樹成2

(1.北京理工大學 北京電動車輛協同創新中心， 北京 100081;2.中國北方車輛研究所 車輛傳動重點實驗室， 北京 100072)

為解決四自由度行星變速機構方案數量大、優選計算復雜的問題，開展四自由度行星變速機構方案性能規律研究。根據四自由度行星傳動的構件之間運動學關系，建立方案模型中制動構件、離合器和輔助構件等系數、各擋傳動比、行星排特性參數、行星輪相對轉速、操縱力矩和效率的數學模型。針對同一機構類型所有可能的方案模型，分析各項性能指標的內部規律，提出按照相同操縱邏輯原則進行構件組模型分類的方法，在傳動方案可行性優選時，對于同一類所有構件組模型只需進行一次計算。通過實例計算表明，該方法有效減小了行星傳動方案優選計算量，提升了方案優選效率。

兵器科學與技術； 四自由度； 行星傳動； 方案性能

0　引言

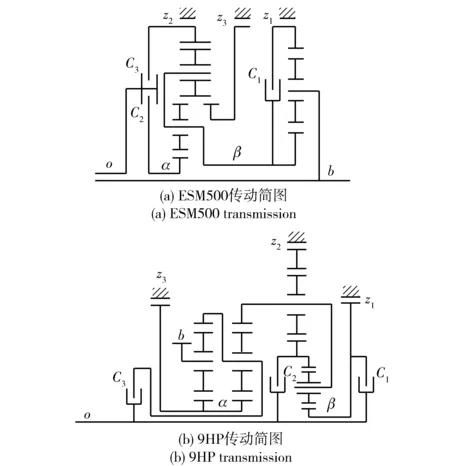
圖1　兩種四自由度變速方案Fig.1　Two 4-DOF gear transmission schemes

多擋化、緊湊化是車輛變速發展的重要方向。隨著車輛變速擋數的增多、行星齒輪制造與裝配技術和電子控制技術的發展，行星變速傳動方案的自由度數也有逐漸增加的趨勢，由早期二自由度發展到三自由度，并逐漸向四自由度傳動方案發展[1-3]，如法國萊克勒爾Soma Minerva ESM500四自由度自動變速器傳動簡圖(見圖1(a))能實現7個不同擋位，其中包括5個前進擋和2個倒擋；德國ZF公司最新推出的9HP四自由度自動變速器傳動方案(見圖1(b))能實現10個不同擋位，其中包括9個前進擋和1個倒擋。此外，德國ZF公司的8AT和日本Aisin公司的 8AT變速器也都采用了四自由度行星自動變速器。四自由度行星變速機構是指在多個行星排構成的行星輪系中具有4個轉速獨立的運動構件，為實現確定擋位需要接合3個操縱元件。四自由度行星變速機構能實現多擋化、空損小和結構尺寸緊湊等顯著優勢[4-7]。圖1中，z1～z3為制動構件，C1～C3為離合器，o為輸入構件，b為輸出構件，α、β為輔助構件。

行星變速方案設計是行星變速機構研制過程中重要的設計階段，是最具有創造性的階段，其難點在于：用多個行星排和操縱元件組成來實現需要傳動比系列的傳動方案，其可能方案數非常多。如用3個行星排、3個制動器和3個離合器組成四自由度方案，理論上可能方案數達到：

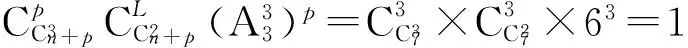
(1)

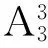
如果在四自由度方案優選時逐一對數以億或數十億計的所有可能的方案模型進行傳動比驗證、行星排特性參數計算和各項性能指標分析，這會帶來計算時間過長的問題，嚴重影響方案設計效率。目前，發達國家對四自由度行星變速方案先進優選理論進行技術封鎖，國內尚未見到成體系的指導理論報道。

若能分析所有方案的內在規律，按規律進行方案分類，將滿足特定規律的模型作為一個整體來分析計算，這樣就可顯著提高方案優選效率并減小計算量。基于這種考慮，本文根據四自由度行星傳動的構件之間運動學關系，通過公式推導來分析所有可能方案的內部規律，并試圖按規律分類進行方案優選。

1　行星傳動運動學特性

對于具有四自由度行星傳動，任意構件x的轉速都可通過輸入構件轉速no、輸出構件轉速nb和任意2個轉速獨立的制動構件轉速nz1、nz2來線性表出，則有[4]

nx=axno+bxnb+cxnz1+dxnz2，

(2)

式中：ax、bx、cx、dx為構件系數。若x為基本構件，則滿足ax+bx+cx+dx=1關系式；若x為離合器，則滿足ax+bx+cx+dx=0關系式。由(2)式可以推導出

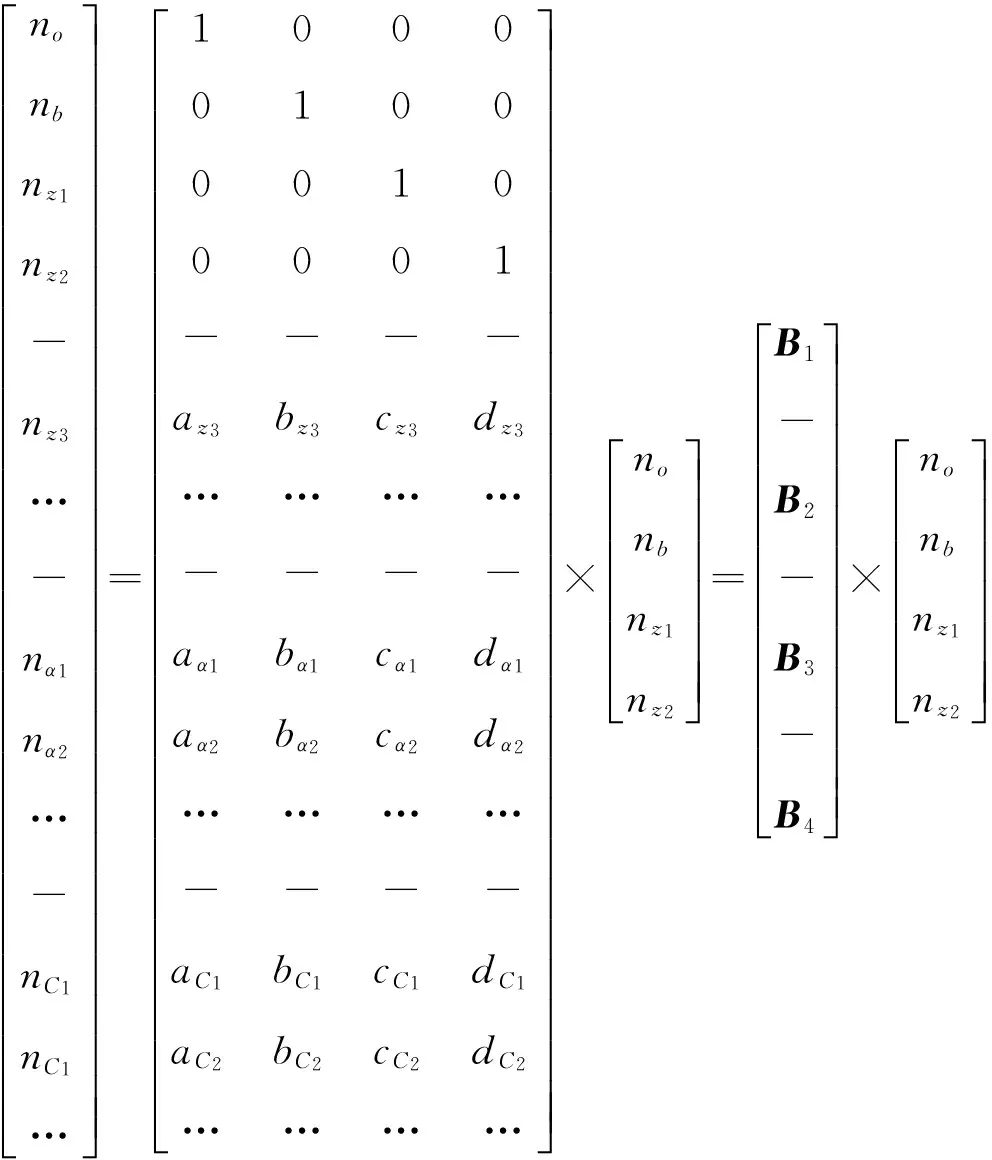
(3)

式中：B1表示獨立構件系數矩陣，為單位矩陣；B2表示制動構件系數矩陣；B3表示輔助構件(除輸入、輸出構件、制動器構件以外的構件稱為輔助構件，反之稱非輔助構件)系數矩陣；B4表示離合器系數矩陣。對于具體結構型式的傳動方案而言。(3)式中各項系數是唯一確定的。

1.1離合器系數計算公式

設離合器Cj用于接合構件x、y，離合器構件系數按(4)式計算：

(4)

1.2制動構件系數計算公式

對于四自由度行星傳動實現一個確定的傳動比，需要接合3個操縱元件，設3個操縱元件為s1、s2、s3，由(2)式可以推導出，當它們接合時對應的傳動比[5]為

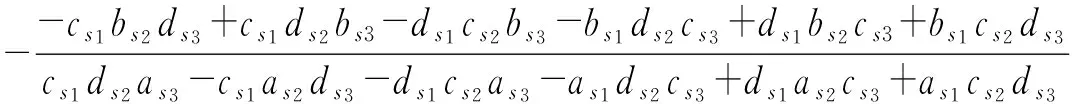
(5)

式中：i[s1,s2,s3]為四自由度方案中接合操縱元件s1、s2、s3對應的傳動比(以下公式中也采用類似表示方式)，s1、s2、s3可以代表某一制動器或離合器。

行星傳動方案所能實現傳動比是方案選擇的主要運動學約束指標。根據傳動比(5)式可以推導出四自由度方案的制動構件系數與傳動比之間的數學模型。不妨令x1=i[z1,z2,zi]，x2=i[z1,z2,Cj]，x3=i[z1,zi,Cj]，x4=i[z2,zi,Cj]，x5=i[z1,Cj,Ck]，x6=i[z2,Cj,Ck]，則有制動構件系數計算公式：

(6)

式中：

ξ=(x2x4-x3x4x6+x3x4x5+x2x3x6-

x3x5x6-x2x6+x2x5+x3x6-x2x4x5-

x4x5+x4x5x6-x2x3)(x1-x2).

(7)

1.3輔助構件系數計算公式

當輔助構件連接2個行星排時(若連接2個以上的行星排時，可以任取2個排)，可以表示為

(8)

式中：行星排p1由x、y、α構件所組成；行星排p2由z、w、α3個構件所組成。由(5)式可以推導出該輔助構件系數與構件x、y、z、w系數之間關系為

(9)

當輔助構件連接1個行星排和1個離合器時，可以表示為

(10)

式中：離合器Cj用于接合構件z、α. 可以推導出該輔助構件系數計算公式為

(11)

當輔助構件連接2個離合器時，可表示為

(12)

式中：離合器Ck用于接合構件y、α. 可以推導出該輔助構件系數計算公式為

(13)

2　行星傳動方案性能指標

2.1行星排廣義特性參數A

對于由構件x、y、z所組成的行星排，存在如下廣義運動學關系[8]：

nx+Any-(1+A)nz=0.

(14)

則特性參數A與構件x、y、z系數之間關系為

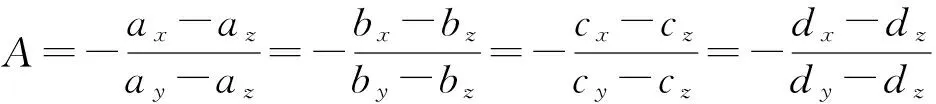
(15)

2.2行星輪相對轉速

根據普通單星行星排計算方法，可以得出行星輪相對轉速為

(16)

式中：s、c、r分別代表構件的太陽輪、框架和齒圈。

2.3操縱力矩

對于沒有外力固定支撐的行星變速機構，作用在機構上外力矩只有輸入構件的驅動力矩、被動構件的負載力矩和操縱力矩，不考慮嚙合損失、軸承和齒輪攪油等損失，則由能量守恒定律可得

Mono+Mbnb+Ms1ns1+Ms2ns2+Ms3ns3=0，

(17)

式中：Mo、Mb、Ms1、Ms2、Ms3分別為輸入構件、輸出構件和3個操縱元件所承受的轉矩。將(2)式代入(16)式中，且令輸入構件轉矩為單位值Mo=1，則3個操縱元件所需操縱力矩為

(18)

當僅有1個制動器zi(i>2)參與接合時，則(18)式轉化為

(19)

對于其他接合方式，可以進行類似推導。

2.4效率模型

采用相對功率法進行方案效率計算，該方法原理簡單，計算容易，且有足夠精度。多排行星傳動效率損失等于各排相對功率損失之和，其效率η計算公式為

1-[(1-ηx1)γ1+(1-ηx2)γ2+…],

(20)

式中：Po為輸入構件功率；Ps1、Ps2分別為各行星排功率損失；ηx1、ηx2分別各行星排的相對運動效率，決定于行星排的嚙合次數和結構，對于普通行星排的相對運動效率取為0.95，雙星行星排的相對運動效率取為0.92；γ1、γ2為各行星排的相對功率系數，計算公式為

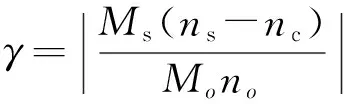
(21)

式中：Ms為行星排太陽輪的轉矩；ns為行星排太陽輪的轉速；nc為行星排框架的轉速。

通過上面所得到的各基本運動件轉速和轉矩，根據(20)式和(21)式就可求出對應工況的傳動效率η.

3　四自由度變速方案的內在規律分析

對于行星傳動方案，根據方案傳動比(5)式以及第2節所列指標計算公式，可以得出如下規律：

1)由(5)式可以得出：具有相同操縱元件操縱邏輯的方案模型，對應的操縱元件系數相同，它們能實現的傳動比是相同的。

2)由(15)式可以得出：對于具有相同操縱邏輯的方案模型，由相同非輔助構件所組成的行星排特性參數A值相同。

3)由(16)式可以得出：具有相同操縱邏輯的方案模型，由相同的非輔助構件所組成的行星排的行星輪相對轉速相同，且任意2個非輔助構件的轉速差相同。

4)由(18)式和(19)式可以得出：具有相同操縱邏輯的方案模型，它們的制動器操縱力矩相同；方案模型中由相同非輔助構件所組成的離合器操縱力矩都相同；對于僅有1個制動器參與操縱的工況，該制動器對應的操縱力矩僅與傳動比有關且等于傳動比減1.

圖2所示為4n3p3Z3L(自由度n=4、行星排數p=3、制動構件數Z=3、離合器數L=3)結構類型中具有相同操縱邏輯的12組方案模型，其中橫線上方每一行表示1個行星排，下方每一行表示1個離合器，“]”表示二自由度機構。

圖2　4n3p3Z3L結構類型中互為相同操縱邏輯的方案模型Fig.2　4n3p3Z3L schemes with same control logic

根據各擋位傳動比數學模型的性質來分，存在著獨立擋和函數擋之分。獨立擋是指這些擋的傳動比在行星排特性參數的合理范圍內可獨立選擇，不受其他擋位傳動比的影響，即與其他傳動比之間無函數關系，在方案設計時易于滿足給定的傳動比要求，獨立擋的各傳動比確定后，函數擋的傳動比也就由函數關系而相應確定，不能獨立選擇[1]。

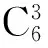
表1　所有可能的結合工況傳動比模型

從表1可以看出，每組方案模型中的各結合工況的傳動比關于u、v、w的表達式相同。按照規律2得出，這些模型中共有的非輔助構件所組成的行星排[b,z1,z3]廣義特性參數A1都等于-1/z.

根據上述規律，圖2所示12組模型是互為相同操縱邏輯的，在尋找所有可行的傳動方案時，可以將每一組模型作為一個整體來進行分析，從而大大減小了方案設計的計算量，若方案選擇時，需同時比較傳動比、行星排特性參數、行星輪相對轉速、操縱力矩4個指標，如果按照相同的操縱邏輯進行歸類處理，那么全部優選計算量是原來的，可見能夠大大減少四自由度方案優選的計算量。

4　四自由度方案優選實例

本文所提出上述方法可適用于單星排和雙星排，對復合排可以拆分成單星排和雙星排的組合進行分析。以法國萊克勒爾Soma Minerva ESM-500變速裝置設計要求為輸入條件，由3個普通單星行星排、3個制動器和3個離合器組成的四自由度傳動方案(即為4n3p3Z3L)，需要實現的各擋傳動比為i1=7.6，i2=4.5，i3=2.86，i4=1.58，i5=1.0，i-1=-1.9，i-2=-5.39. 依據車輛總體性能匹配要求，各擋傳動比允許的相對誤差為R1=0.05，R2=0.02，R3=0.01，R4=0.01，R5=0，R-1=0.01，R-2=0.05，行星排特性參數A為1.45～4.50，行星輪相對轉速npc≤3.0no，操縱力矩Mφ≤5.0Mo，各擋位傳動效率η≥0.80(設置較低的傳動效率閾值，主要為了方案優選時提供更多的可行備選方案，實際優選出的方案效率一般大于0.9)。

將上面設計條件輸入到該設計系統中，計算大約需要計算時間5 h(以某Intel酷睿II雙核2.83 GHz處理器的PC機機時計算)，得出87個滿足傳動比系列且行星排特性參數合理的方案，進一步對其進行性能和結構分析知，僅有5個可行方案，如圖3所示，圖3(a)～圖3(d) 4個方案為具有相同操縱邏輯的方案，各擋位下z1、z2、z3制動構件操縱力矩相同；由相同構件組成的行星排特性參數相同及其各擋位下行星輪相對轉速相同，如方案1和方案2的第1、第3行星排太陽輪、行星架和齒圈都是由相同構件組成，致使第1、第3行星排A值相同及其各擋位下行星輪相對轉速都相同，但第2行星排太陽輪、行星架和齒圈不是由相同構件組成，致使第2行星排A值不同及其各擋位下行星輪相對轉速也不相同，驗證了相同操縱邏輯的方案下相同構件組成的行星排A值及其各擋位下行星輪相對轉速相同的分析結論；由相同構件組成的離合器操縱力矩相同，如方案1和方案2的C1、C2和C33個離合器都是用于接合相同兩個構件，致使這3個離合器各擋位下操縱力矩都相同(參見表2～表4)。圖3(e)中方案5與前4種方案為具有不同操縱元件的方案(見表(3))。

考慮到可以采用復合行星排代替單星排和雙星排，將圖3(a)方案的第1排行星架和齒圈進行互換，行星排由普通單星行星排變成了雙星行星排，對應行星排特性參數為-2.9，即可獲得Soma Minerva ESM-500行星變速機構方案。這也驗證了本文所提出的規律的正確性。

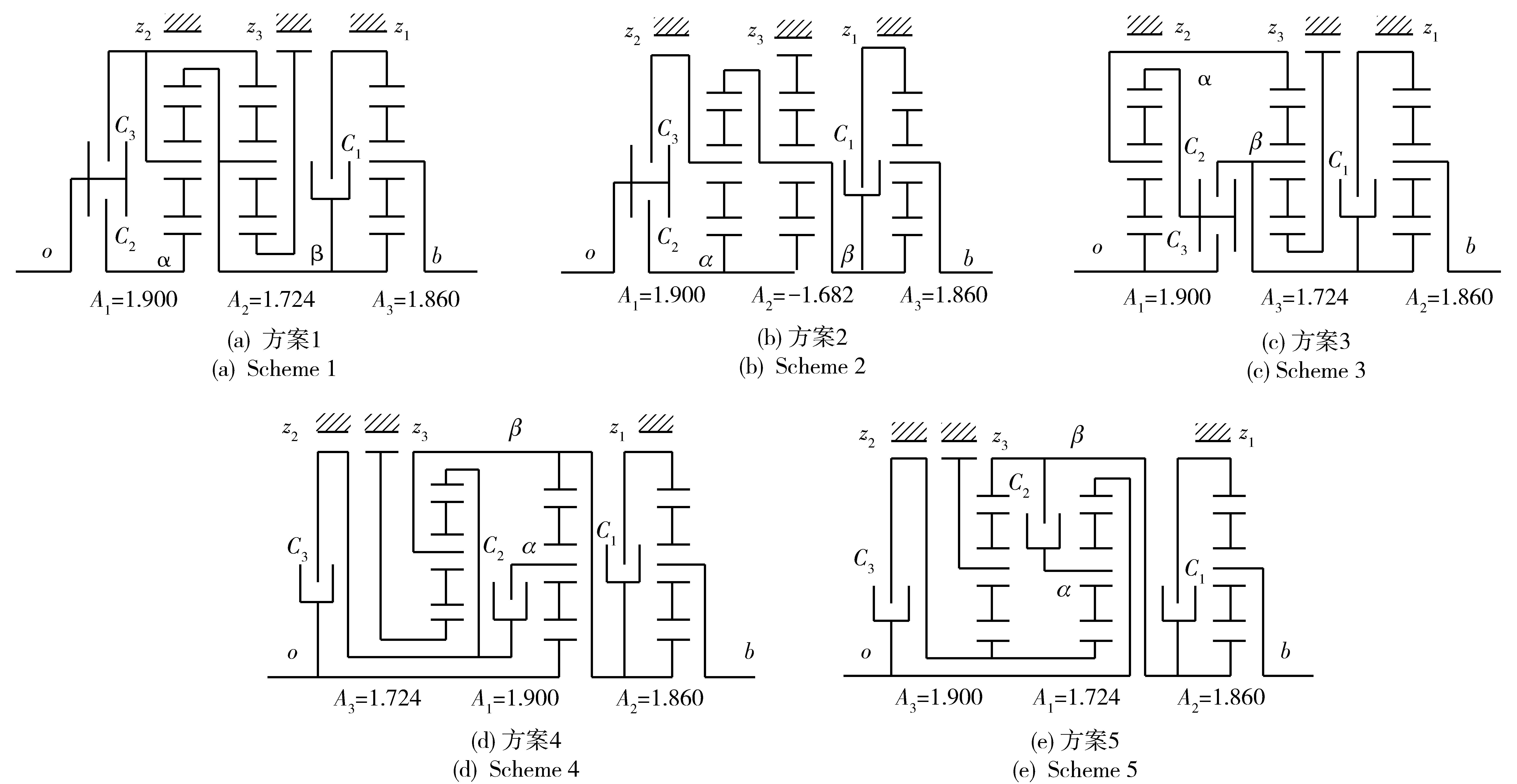
圖3　5個性能較優且滿足設計需求的可行方案Fig.3　5 feasible schemes to meet the design requirements

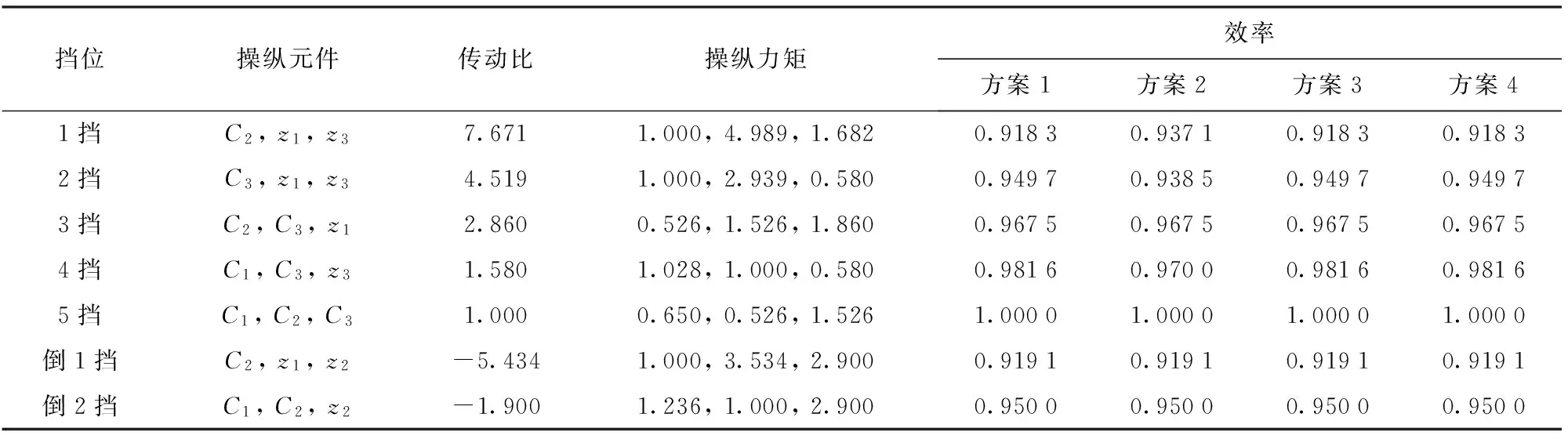
擋位操縱元件傳動比操縱力矩效率方案1方案2方案3方案41擋C2,z1,z37.6711.000,4.989,1.6820.91830.93710.91830.91832擋C3,z1,z34.5191.000,2.939,0.5800.94970.93850.94970.94973擋C2,C3,z12.8600.526,1.526,1.8600.96750.96750.96750.96754擋C1,C3,z31.5801.028,1.000,0.5800.98160.97000.98160.98165擋C1,C2,C31.0000.650,0.526,1.5261.00001.00001.00001.0000倒1擋C2,z1,z2-5.4341.000,3.534,2.9000.91910.91910.91910.9191倒2擋C1,C2,z2-1.9001.236,1.000,2.9000.95000.95000.95000.9500

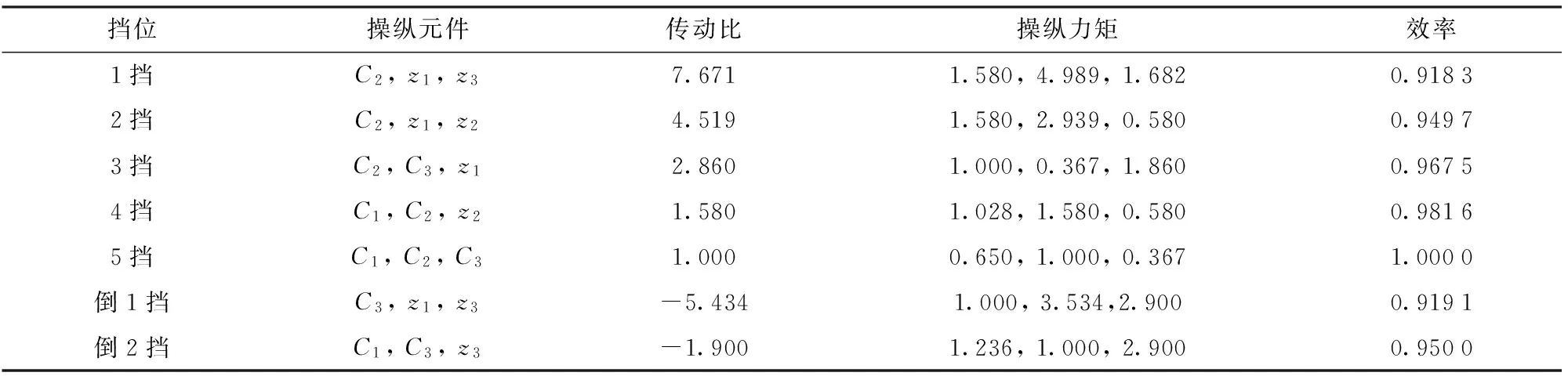
表3　方案5計算結果

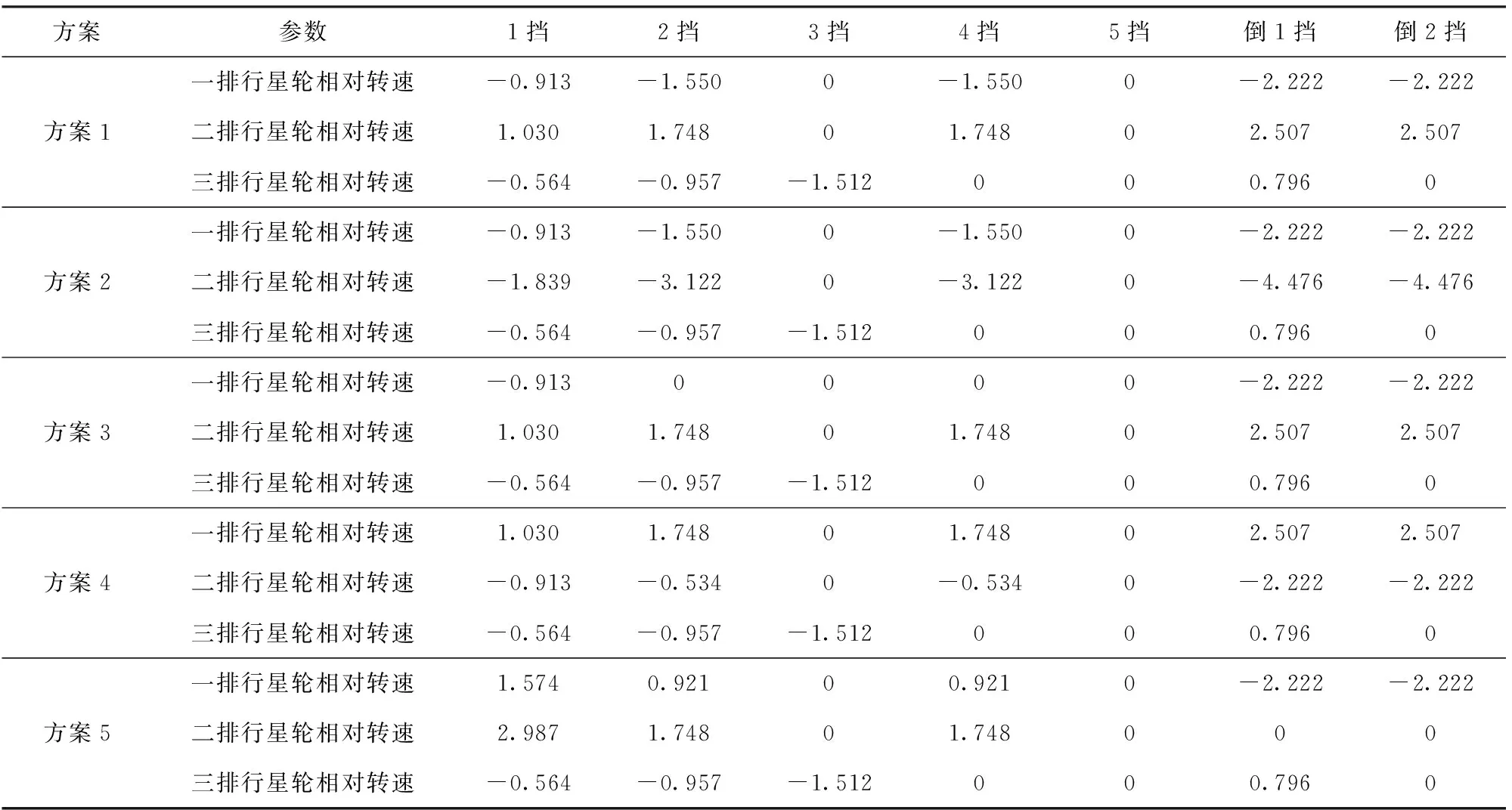
表4　各方案行星輪相對轉速

5　結論

1)根據行星傳動性能指標的計算公式，找到了相同操縱邏輯的構件組模型能實現的傳動比、由相同非輔助構件所組成的行星排特性參數及其行星輪相對轉速、由相同的非輔助構件所組成的離合器操縱力矩和制動器操縱力矩之間的規律，這些指標之間的規律，可以用于指導四自由度行星傳動方案優選。

2)以操縱邏輯相同為原則對構件組模型進行分類，在傳動方案可行性優選時，對于同一類的所有構件組模型只需進行一次計算，包括驗證各擋傳動比是否在允許的誤差范圍內，以及非輔助構件所組成的行星排特性參數是否合理，這樣可以有效地減小方案優選時間和計算量，提高方案設計效率。

References)

[1]李慎龍. 基于圖論的行星變速傳動方案計算機輔助設計[D]. 北京:北京理工大學, 2009.

LI Shen-long. Computer aided design of planetary transmission scheme based on graph theory [D]. Beijing: Beijing Institute of Technology, 2009. (in Chinese)

[2]劉修驥. 汽車型行星變速箱設計[M]. 北京：北京工業學院，1975.

LIU Xiu-ji. Design of automobile planetary gear transmission [M]. Beijing: Beijing Institute of Technology, 1975.(in Chinese)

[3]Liu X J. Design of muti-speed of planetary transmission[M]. Beijing: Beijing Institute of Technology Press, 1992.

[4]劉修驥. 車輛傳動系統分析[M]. 北京:國防工業出版社, 1998.

LIU Xiu-ji. Analysis of vehicle transmission system [M]. Beijing: National Defense Industry Press, 1998.(in Chinese)

[5]萬耀青, 劉太來. 行星變速箱方案選擇理論與優化[M]. 北京:國防工業出版社, 1997.

WAN Yao-qing, LIU Tai-lai. Planetary transmission scheme selection theory and optimization[M]. Beijing: National Defense Industry Press, 1997.(in Chinese)

[6]Gumpoltsberger G. Systematische synthese und bewertung von mehrg?ngigen planetengetrieben[D]. Chemnitz: Technischen Universit?t Chemnitz, 2010.

[7]J?rg Müller. Beitrag zur systematischen, rechnergestützten synthese und bewertung mehrg?ngiger konventioneller und hybrider planetenautomatikgetriebe[D]. Chemnitz: Technischen Univer-sit?t Chemnitz, 2011.

[8]饒振鋼. 行星傳動機構設計[M]. 北京:國防工業出版社，2004.

RAO Zhen-gang. Design of planetary transmission mechanism[M]. Beijing: National Defense Industry Press, 2004. (in Chinese)

Study of Scheme Characteristics of 4-DOF Planetary Gear Transmission Mechanism

LI Shen-long1,2, MAO Ming2, GAI Jiang-tao2, LIU Shu-cheng2

(1.Collaborative Innovation Center of Electric Vehicles in Beijing, Beijing Institute of Technology, Beijing 100081, China; 2.Science and Technology on Vehicle Transmission Laboratory， China North Vehicle Research Institute， Beijing 100072， China)

In order to solve a huge amount of complex optimization calculation of 4-DOF planetary gear mechanism schemes, the scheme characteristics of four-degrees-of-freedom planetary gear transmission mechanism are studied. According to the kinematic relationship among the components of four degrees-of-freedom planetary gear transmission, a mathematical model is established for the coefficients of braking component, clutch and auxiliary component, the gear ratios, the characteristic parameter of planetary gear row, the relative speed of planetary gear, the control torque and efficiency in scheme model. For all possible scheme models with same mechanism, the internal rules of the performance indexes are analyzed to provide a theoretical basis for model classification. A method of component group model classification based on the same control logic principle is put forward. The same kind of component group models can be calculated for one time by using the proposed method for choice of feasibe transmission schemes. The calculated results shows that the proposed method can be used to reduce the optimization calculation of planetary transmission schemes, and improve its efficiency.

ordnance science and technology; 4-DOF; planetary gear transmission; scheme performance

2016-01-07

國家探索研究項目(7131458)

李慎龍(1982—)，男，研究員，博士。E-mail: lishenlong2004@sina.com；

劉樹成(1986—)，男，工程師，博士。E-mail:liushucheng@vip.126.com

TJ81+0.321

A

1000-1093(2016)10-1770-08

10.3969/j.issn.1000-1093.2016.10.002