巖石動力學計算中的網格效應及機理研究

王海兵， 張海波， 田宙， 歐卓成， 周剛

(1.北京理工大學 爆炸科學與技術國家重點實驗室, 北京 100081; 2.西北核技術研究所, 陜西 西安 710024)

?

巖石動力學計算中的網格效應及機理研究

王海兵1,2， 張海波2， 田宙2， 歐卓成1， 周剛2

(1.北京理工大學 爆炸科學與技術國家重點實驗室, 北京 100081; 2.西北核技術研究所, 陜西 西安 710024)

巖石動力學計算中，網格尺寸對數值計算結果的可靠性有重要影響。采用數值實驗的方法，對巖石爆炸應力波傳播數值計算中的網格尺寸效應及其敏感性機理進行了研究。研究結果表明：合適的網格尺寸要根據載荷特征和波傳播介質的屬性來決定；當一個載荷波長內的網格數達到16個以上時，計算得到的各物理量的波形和峰值基本趨于穩定；計算還給出了各物理量與網格密度的關系；隨著爆心距的增加，物理量對網格尺寸的敏感性降低，其機理是載荷中的高頻成分逐漸衰減、載荷的波長變大，模型所需的網格尺寸變大；時間步長系數對計算結果的影響也非常明顯，當時間步長系數取0.05時，位移穩態值趨于收斂值。

兵器科學與技術； 數值計算； 網格尺寸； 時間步長； 敏感性機理

0　引言

巖石中的爆炸動力學問題廣泛應用于國家經濟建設、國防軍事以及科研領域等方面。巖石中的爆炸動力學過程非常復雜，通常很難進行精確地解析求解，數值計算是常用的有效手段。該方面的計算主要涉及三方面的物理過程：一是炸藥的起爆及爆炸產物與沖擊波在爆室內的傳播；二是爆炸產物及沖擊波與圍巖的相互作用；三是圍巖的動態響應。與這三方面物理過程相對應的三類計算問題為：爆炸載荷的求解問題、爆炸載荷與圍巖的能量耦合問題以及應力波在圍巖中的傳播問題。計算這些問題常用的數值方法是有限差分方法和有限元方法。與有限差分相比，有限元方法具有靈活的網格劃分、邊界條件和邊界形狀的處理等優點，現在已成為爆炸動力學中的重要數值方法。通常來講，數值計算的精度依賴于描述材料行為所采用的數學模型，如本構關系和狀態方程等。由于目前描述爆炸作用下材料響應的數學模型還不完善，且都是近似的，因此數值分析的精度一般不高于近似方程的精度[1]。如果不考慮數學模型的近似程度，單從數值計算的角度講，一種算法的穩定性與精度決定于[2]：1)積分格式與其所用的參數；2)時間步長；3)計算模型所劃分的網格尺寸。

由于爆炸波持續時間非常短并且能量在不同的網格之間傳輸，數值模擬結果對有限單元的尺寸非常敏感，數值結果的精度強烈地依賴于所使用的網格尺寸。通常需要開展網格尺寸收斂性測試以獲得合適的網格尺寸。爆炸沖擊波數值模擬中網格尺寸效應研究的核心問題就在于如何針對具體的爆炸問題確定合適的網格尺寸，以在確保數值模擬精度的同時盡可能地減少網格數量和提高計算效率。然而，由于各類介質的物理屬性差異，使得針對某一種介質開展網格尺寸效應分析確定的網格尺寸在介質改變時，其適用性具有較大的局限性。采用同一網格尺寸模擬不同介質中的沖擊波傳播問題時，計算精度可能存在較大區別。因此，合適的網格尺寸不僅與所模擬的爆炸情況相關，還與爆炸沖擊波的傳播介質相關[3]。當爆炸載荷作用在爆室壁圍巖時，就涉及流體與固體(簡稱流固)耦合問題，研究表明，流固耦合算法的選取及關鍵耦合參數的設置以及爆炸流體和圍巖固體網格尺寸的相對大小，對計算結果都有很大的影響。限于篇幅限制，本文關于網格尺寸對流固耦合效果的影響暫不展開討論，主要研究爆炸沖擊波在空氣中及巖石內傳播的網格尺寸效應。

1　網格尺寸對爆炸場載荷計算的影響

爆炸載荷的確定依賴于爆炸場的求解，也直接影響著外圍結構響應的計算和安全性評估的可靠性，因此準確的爆炸載荷計算非常重要。一般情況下，爆室或容器內的爆炸屬于近區爆炸，在爆炸近區，爆轟產物的密度遠高于空氣密度，產物對爆炸載荷有著顯著的影響。對此，國內外學者已開展了諸多研究，研究結果表明，在爆炸近區網格尺寸對計算結果的精度影響非常敏感。胡八一等[4]指出，要想模擬出來的反射沖擊波壓力峰值及波形與實測波形一致，最為關鍵的一點是爆室內或容器內部網格尺寸至少應小于或等于1 mm. Chapman[5]在用類似的商業軟件計算沖擊波超壓時也發現當網格由10 mm細化到1 mm時，超壓峰值提高了24.6%. 文獻[6-7]的計算結果顯示，采用LS-DYNA等商業軟件計算得到的計算結果小于經驗公式值，受軟件和計算機硬件容量的限制，只能提供定性的計算結果，很難提供準確的定量計算。雷鳴等[8]采用Autodyn研究了網格大小對空中化爆自由場參數計算結果的影響，結果表明網格大小對質量守恒沒有影響，對能量守恒有一定的影響，爆炸產物界面第一次擴張是在大約0.9 m/kg1/3爆心距位置附近，在比例距離1 m/kg1/3內每個單元取0.5 mm，在更遠的區域每個單元5 mm計算得到的值與標準實驗值較符合較好。姚成寶等[9]利用LS-DYNA計算空中爆炸時發現，網格尺寸在0.1～5 mm時計算結果差別不大，在網格尺寸小于1 mm時計算結果趨于收斂，當網格的密度尺寸小于5 mm/kg1/3時，計算結果基本趨于收斂，此時得到的結果基本滿足精度要求。王海兵等[10]采用二維方法研究了容器內的爆炸載荷，結果指出：在比距離小于1.0 m/kg1/3時，2 mm的網格尺寸計算結果趨于收斂；在比距離大于1.0 m/kg1/3、網格尺寸取5 mm時，計算得到的峰值超壓基本滿足精度。Shi等[11]詳細比較了網格尺寸對空中爆炸自由場諸參量的影響，圖1～圖3給出了其主要結果。圖1給出了不同網格尺寸在比距離R為1 m/kg1/3處的正超壓時程曲線比較，從圖中可看出，隨著網格尺寸的增加，壓力p的上升率減緩、波形變得平緩、波幅拉寬，峰值降低；但波前到達時間和正壓作用時間與網格尺寸無關。圖2為峰值超壓與網格尺寸和比距離的關系，從圖中看出，當比距離小于0.8 m/kg1/3時，即使5 mm的網格尺寸也不能準確計算峰壓；而當比距離超過2 m/kg1/3時，100 mm的網格尺寸也能準確地計算峰壓。圖3給出了正壓沖量I與網格尺寸和比距離的關系，從圖中看出，正壓沖量與網格尺寸基本無關，100 mm的網格尺寸已能達到計算收斂?？偨Y以上學者的研究結果，可以得到以下結論：當爆炸近區的網格尺寸取毫米量級時，可使計算獲得的所有力學參量符合實測；隨著網格尺寸的增加，壓力的上升率減緩、波形變得平緩、波幅拉寬，峰值降低；超壓峰值對網格的敏感性很高，隨著比距離的增加，超壓峰值對網格的敏感降低；超壓峰值和壓力上升率是網格密度的正相關量，而波前到達時間、正壓作用時間、正壓沖量等是網格尺寸的無關量。

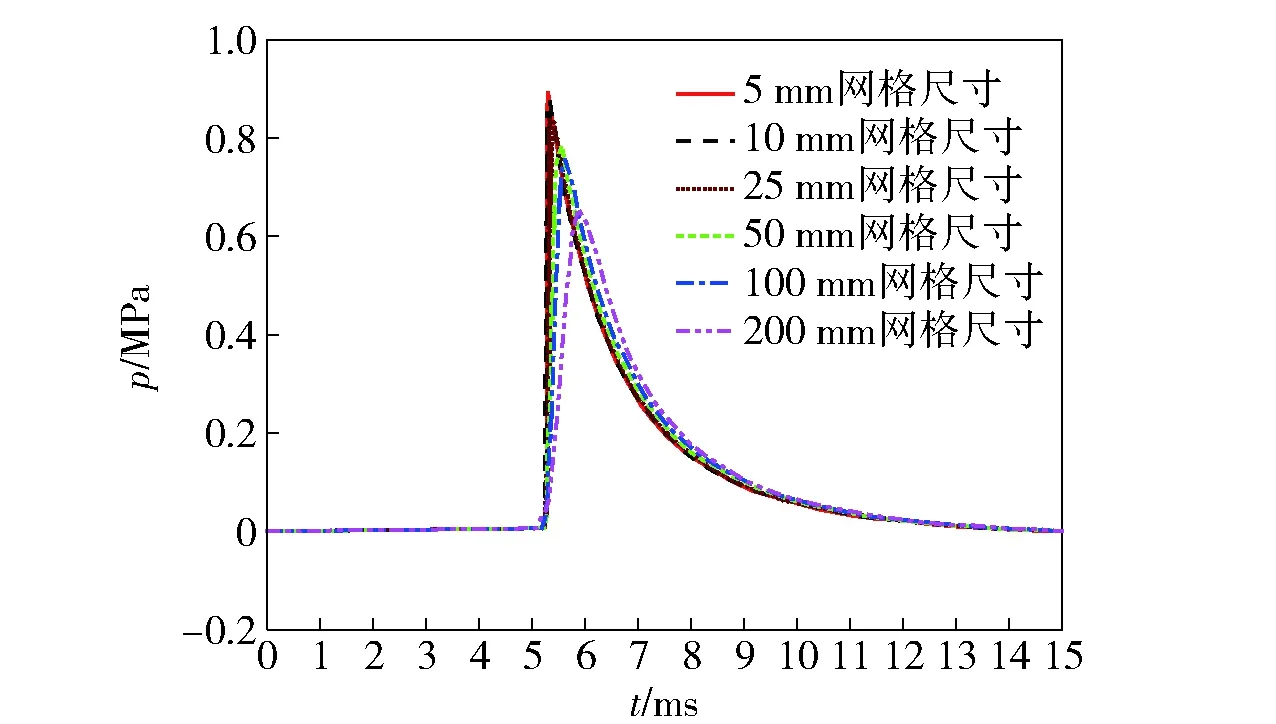
圖1　　　　不同網格尺寸在比距離1 m/kg1/3處的正超壓時程曲線比較[11]Fig.1　　　　Comparison of pressure-time histories obtained with different mesh sizes at scaled distance of 1 m/kg1/3[11]

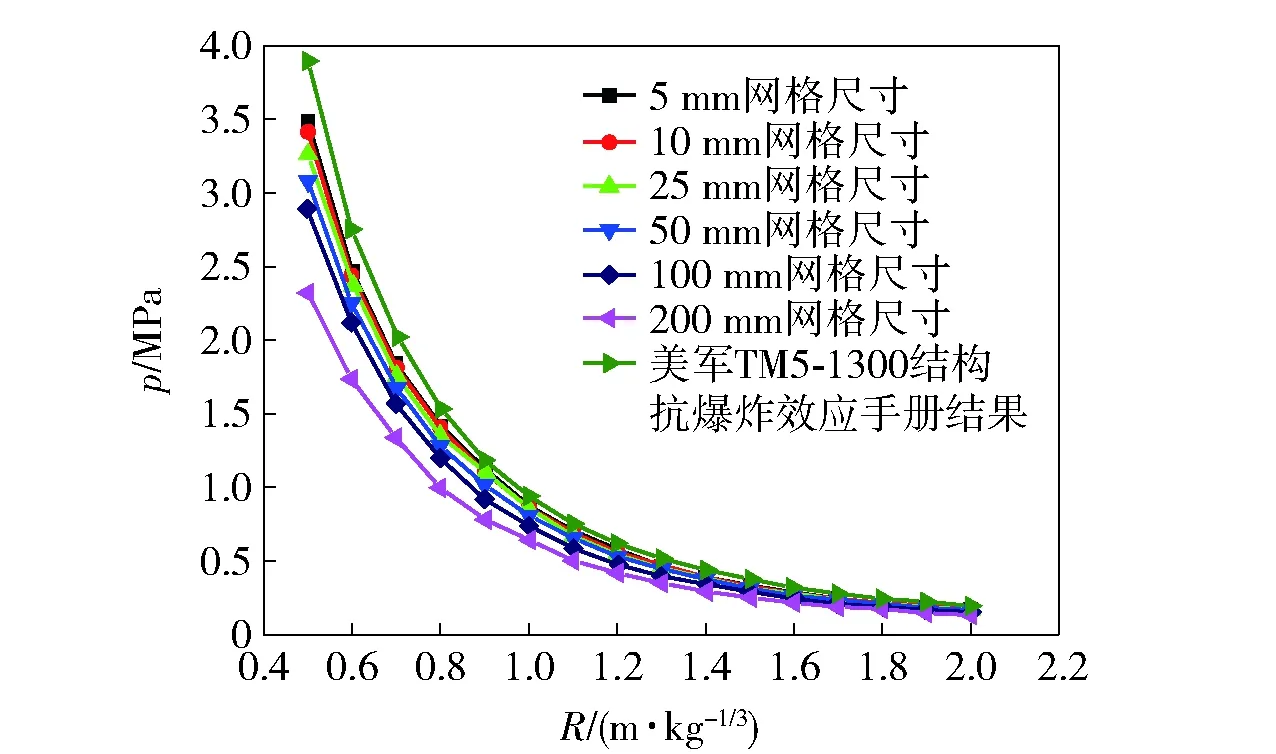
圖2　峰壓與網格尺寸和比距離的關系[11]Fig.2　　　　Variation of the positive incident peak pressure with mesh size and scaled distance[11]

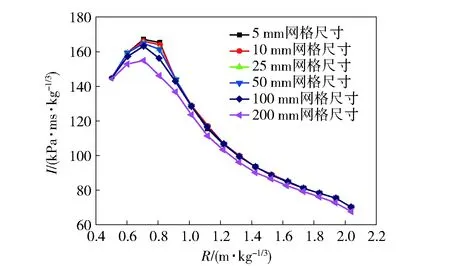
圖3　正壓沖量與網格尺寸和比距離的關系[11]Fig.3　　　　Variation of normalized positive incident impulse with mesh size and scaled distance[11]

在實際應用中，要使計算達到工程使用價值，計算模型的尺度至少要達到1～10 m的范圍，在如此大的范圍內，若將所有的力學參量都計算準確，需要將單元尺寸細化到毫米量級。對于三維計算，即使采取1/8對稱模型，網格數量也將達到109～1012個量級左右。這樣的計算規模即使采用目前最為先進的巨型工作站進行計算，也絕非易事。但通常關注的效應是爆炸作用下的結構響應，而決定結構響應的參量是正壓沖量。前文的網格收斂性計算說明，正壓沖量是網格尺寸的不敏感量，100 mm的網格尺寸已經能基本滿足計算精度要求。所以，當計算規模較大時，雖然由于網格尺寸限制，不能對超壓峰值進行準確計算，但仍然能夠準確計算正壓沖量，進而能夠獲得準確的爆炸效應。文獻[11]還提出一種網格尺寸效應的數值修正方法，其原理是利用網格尺寸的不敏感量來修正網格尺寸敏感量，從而提高大網格尺寸情況下有限元模擬結果的精度。具體方法是通過沖量等效的原理來修正超壓峰值，修正后，即使采用200 mm的網格尺寸也能得到較為精確的超壓峰值。

2　網格尺寸對巖石中應力波傳播計算的影響

關于網格尺寸對巖石動力學計算的影響，已有學者開展了相關的研究。梁正召等[12]討論了非均勻性巖石中網格尺寸對裂紋擴展即巖石破裂的影響，研究認為，隨著網格尺寸的減小，巖石強度逐漸降低，并趨于穩定；在均質巖石中，網格尺寸主要和結構特征相關；在非均質巖石中，網格尺寸還與材料的非均勻性和細觀特征尺度密切相關，引入單元統計性的非均勻性后，單元尺寸必須接近細觀特征尺度才能保證計算結果的穩定性和可靠性。崔煥平等[13]提出了把極限拉應變作為網格尺寸的函數，以保證混凝土開裂單位面積吸收的能量唯一，從而有效地消除混凝土非線性有限元分析中的網格尺寸效應。門建兵等[14]研究了網格對混凝土侵徹數值模擬的影響，研究認為彈丸半徑方向要劃分3個網格，靶板在彈丸半徑尺寸方向上劃分6個網格得到的計算結果比較理想。Shayanfar等[15]討論了網格尺寸對載荷- 位移、載荷- 應變、裂紋模式和最終載荷的影響，并開發了一個簡單的程序來計算混凝土的最終拉伸應變，以此來消除計算結果對網格尺寸的依賴，并將其嵌入到非線性有限元程序中。以上的研究大多都是通過網格的收斂性測試來獲得合適的網格尺寸，然而對于大規模計算來講，很難對模型進行整體的網格收斂性測試；另外，這些研究并未考慮載荷的特征，而爆炸沖擊型載荷包含大量的高頻分量，其輸入荷載的波形與模型網格劃分密切相關，如果不同時考慮荷載的頻譜特性，在確定時間步長和網格劃分時往往帶有較大的盲目性，得到的結果也不具備一般通用性。因此，本文以輸入載荷的特性為出發點，來研究網格尺寸對巖石中應力波傳播計算的影響。

2.1典型的爆炸載荷特征

以1 t TNT爆炸為例，讀取爆心距3.06 m位置處的壓力波形如圖4所示。從圖4中的載荷等效曲線確定外載荷的周期約為300 μs.

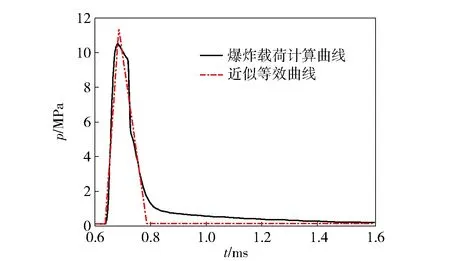
圖4　1 t TNT爆炸在3.06 m位置處的壓力波形Fig.4　　　　Pressure waveform at 3.06 m from the distance of 1 t TNT explosive source

2.2巖石中的波速及波長

彈性波傳播的速度不僅僅取決于波的類型，而且還與介質周圍的條件有關。彈性縱波在單軸應變(相當于無限介質)條件下傳播的速度為

(1)

式中：ρ、Λ和μ分別是介質的密度、拉梅常數和剪切模量；cim是彈性波在無限介質中的傳播速度。

對于一維桿的波傳播問題，根據波動方程，有

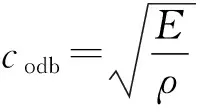
(2)

式中：E是彈性模量；codb是彈性波在一維桿中的傳播速度?！盁o限介質”和“桿”等模型都是一些極限情況的近似，所謂“無限介質”是指在物理上介質的尺度遠遠大于所傳播波的波長，“桿”是指介質的橫向尺度遠遠小于波的波長。通常研究的介質其尺度各不相同，研究的波長也從地震波的幾百千米至實驗室內超聲波波長的幾個毫米乃至幾微米不等。因此，在討論波速及波傳播問題時，需要研究介質的尺度與波長λ大小的相互關系。取花崗巖參數：密度為2.62 g/cm3，泊松比υ為0.24，彈性模量為58.7 GPa. 再根據彈性力學關系式：

(3)

(4)

得到彈性縱波在花崗巖無限介質中的傳播速度cim=5 138 m/s，在花崗巖中一維桿的波速codb=4 733 m/s.

因此，2.1節中的爆炸載荷在花崗巖無限介質中傳播的波長為

λim=cimT=1.541 4 m，

(5)

式中：T為載荷加載周期。

在花崗巖介質一維桿中傳播時的波長為

λodb=codbT=1.419 9 m.

(6)

由此看到，應力波的波長由外載荷和傳播介質的屬性共同決定。

2.3巖石中波傳播計算所需的網格尺寸

下面研究當網格尺寸取多少時，巖石中的波傳播計算結果趨于穩定。

建立一維桿模型，計算桿中的彈性波傳播問題。在桿的端部施加半周期正弦載荷F=Asinωt，其中，A為振幅，ω為角頻率，頻率f=1/T=ω/2π. 取T=300 μs，A=10 MPa，低于巖石強度，彈性加載。輸入的加載波形如圖5所示。

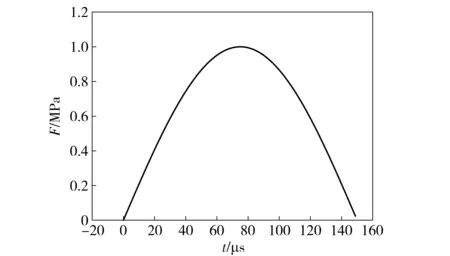
圖5　輸入的壓力加載波形Fig.5　Loading waveform of input pressure

區別于大多數文獻中通過逐漸減小網格尺寸加密網格數來獲得網格收斂性結果的方法，本文將網格尺寸和載荷波長相關聯，研究一個波長長度內不同網格數對計算各物理量的影響。取網格尺寸Δl=λ/n，其中n為網格密度數，表示一個波長長度內的網格數，λ取花崗巖一維桿中的波長1.419 9 m.n分別取2、4、8、16、20、40和60.

2.3.1網格尺寸對壓力波形的影響

圖6給出了一個波長范圍內取不同網格數計算得到的壓力波形比較。從圖6中可以看出：壓力的波形和峰值對網格密度非常敏感，當一個波長內的網格達到16個時，壓力波形和峰值基本趨于穩定；隨著網格密度的增大，壓力波形的首峰上升率增大、振蕩次數減少、振蕩頻率減小；壓力波形以最終穩態值為中心進行振蕩，不同網格密度計算得到的最終壓力穩態值相同。

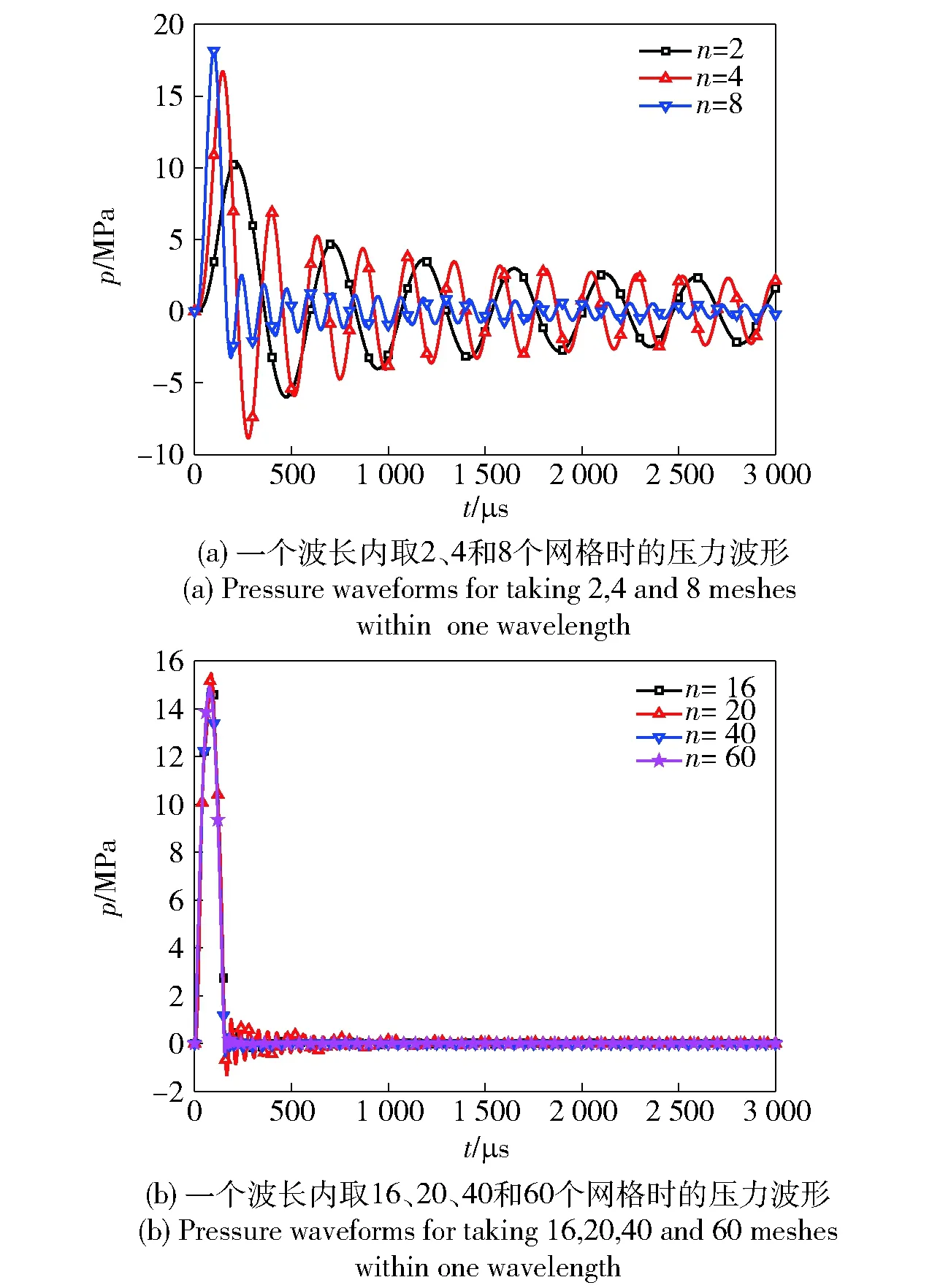
圖6　　　　一個波長范圍內取不同網格數計算得到的壓力波形比較Fig.6　Comparison of pressure waveforms obtained from different grid number within a wavelength range

2.3.2網格尺寸對速度波形的影響

圖7給出了一個波長范圍內取不同網格數計算得到的速度v波形比較。從圖7中可以看出：隨著網格密度的增大，速度峰值逐漸增大，速度波形的首峰上升率增大；當網格密度達到16時，速度峰值和波形基本趨于穩定值；隨著網格密度的增大，速度波形的振蕩(次數和周期)逐漸減少。

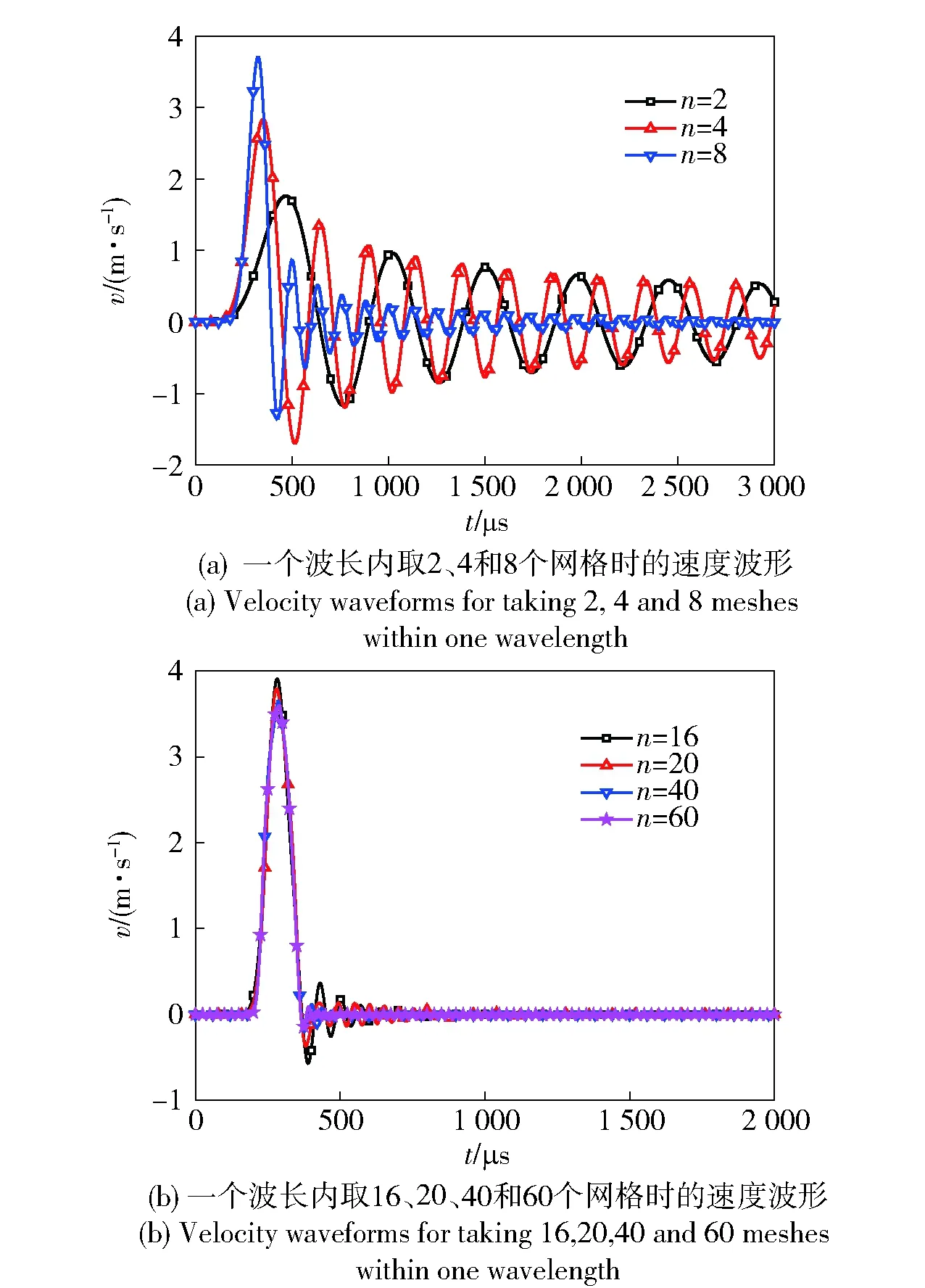
圖7　一個波長范圍不同網格數計算得到的速度波形比較Fig.7　Comparison of velocity waveforms obtained from different grid numbers within a wavelength range

2.3.3網格尺寸對位移波形的影響

圖8給出了一個波長范圍內取不同網格數時計算得到的位移D波形比較。從圖8中可以看出：隨著網格密度的增大，位移峰值逐漸減小、首峰上升率增大、位移波形的振蕩周期逐漸減小、振蕩次數逐漸減少；當每個波長內的網格數量達到16時，位移峰值和波形基本趨于穩定；比較不同網格密度的位移波形可以看到，雖然波形不同、振蕩周期不同，但位移的穩態值基本相同(振蕩波形取穩態值為波峰或波谷間的平均值)。由此可認為，位移的波形和峰值受網格尺寸影響明顯，但位移穩態值與網格尺寸無關，穩態位移值是網格無關量。為證明該結論的正確性，下面進行進一步計算驗證。

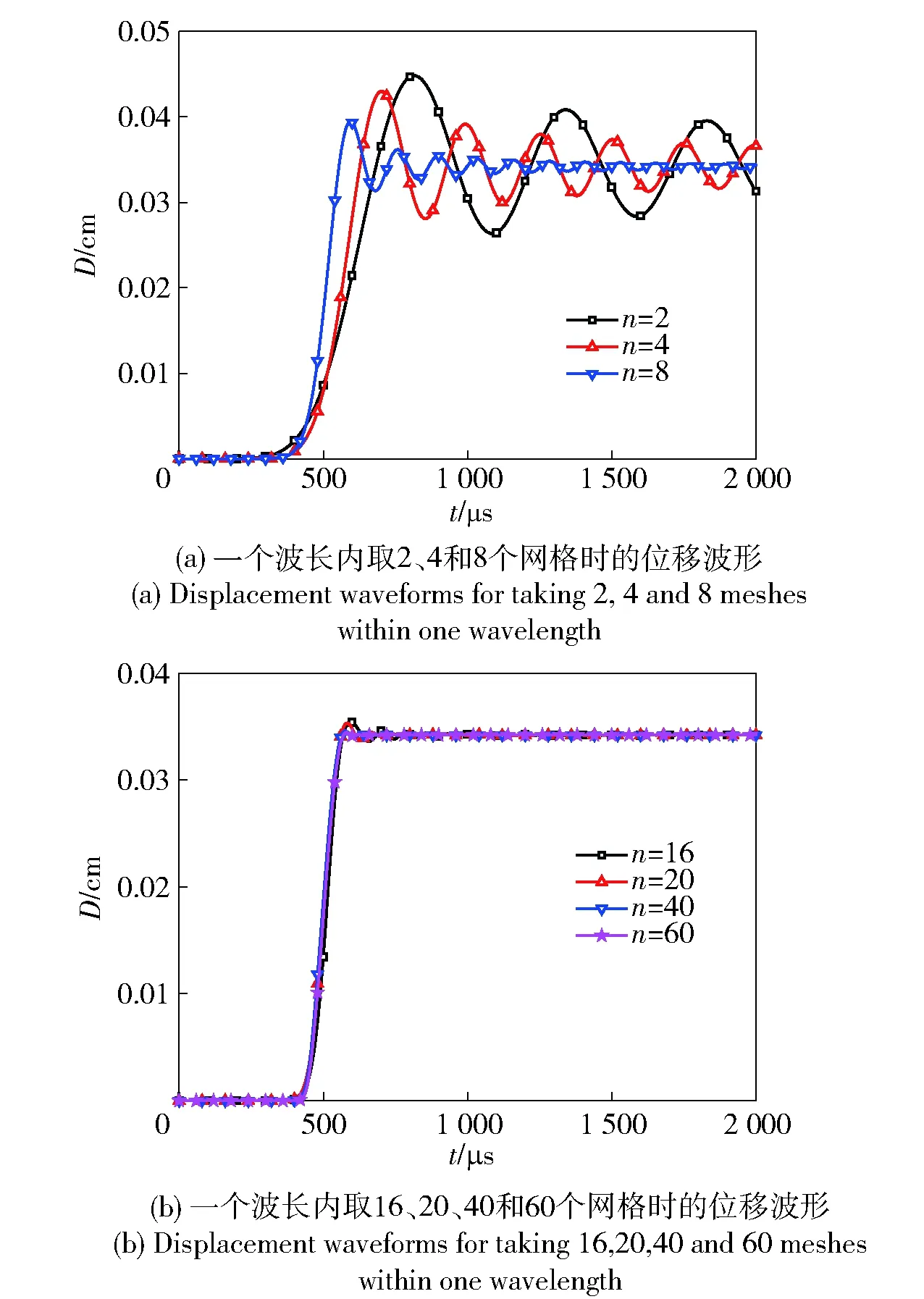
圖8　　　　一個波長范圍不同網格數計算得到的位移波形比較Fig.8　Comparison of displacement waveforms obtained from different grid numbers within a wavelength range

首先進一步減小網格密度(增大網格尺寸)，比較位移波形和穩態值。計算中增加桿長、增加計算時間，將網格密度進一步減小到一個波長一個網格和兩個波長一個網格，比較不同網格密度計算得到的位移波形，如圖9所示。圖9中標出了不同網格密度計算得到的位移穩態值，從圖中看到，不同網格密度計算得到的位移穩態值完全相同。

圖9　一個波長范圍內不同網格數計算得到的位移波形比較Fig.9　Comparison of displacement waveforms obtained from different grid numbers within a wavelength range

另外，為了驗證加載波類型對結論的影響，將加載波由半周期正弦波改為單脈沖方波，對不同網格密度進行計算驗證，計算得到了同樣的結論：當一個波長內的網格數從1個增加到32個時，計算得到的穩態位移值完全相同；但網格密度不同，計算到達穩態位移所需的時間不同，網格密度越大，計算達到穩態位移的時間越短。該驗證說明，獲得的上述結論和加載波的類型無關。

從能量的角度可以解釋穩態位移計算結果的網格無關性。對各種不同的網格密度模型輸入的外力載荷相同，因此對模型做的總功相同。而功等于力與位移的乘積，如果計算中能量守恒，輸入的外載荷又相同，那么得到的穩態位移值一定相等。

2.3.4巖石中爆炸波傳播計算所需的網格尺寸

根據2.3.3節得到的結論，當一個波長內的網格數達到16個時，計算波形基本趨于穩定，計算結果基本收斂，可以推算花崗巖無限介質中爆炸波傳播計算所需的網格尺寸為

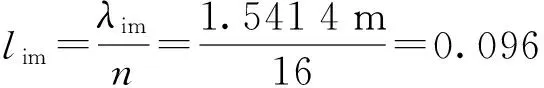
(7)

花崗巖介質中一維桿波傳播計算所需的網格尺寸為

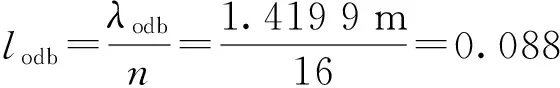
(8)

根據計算得到的網格尺寸，測試圍巖自由場計算精度，結果如圖10所示，圖中，vmax為速度峰值，d為爆心距。從圖10中看到，10 cm的網格尺寸，基本能滿足計算精度要求。

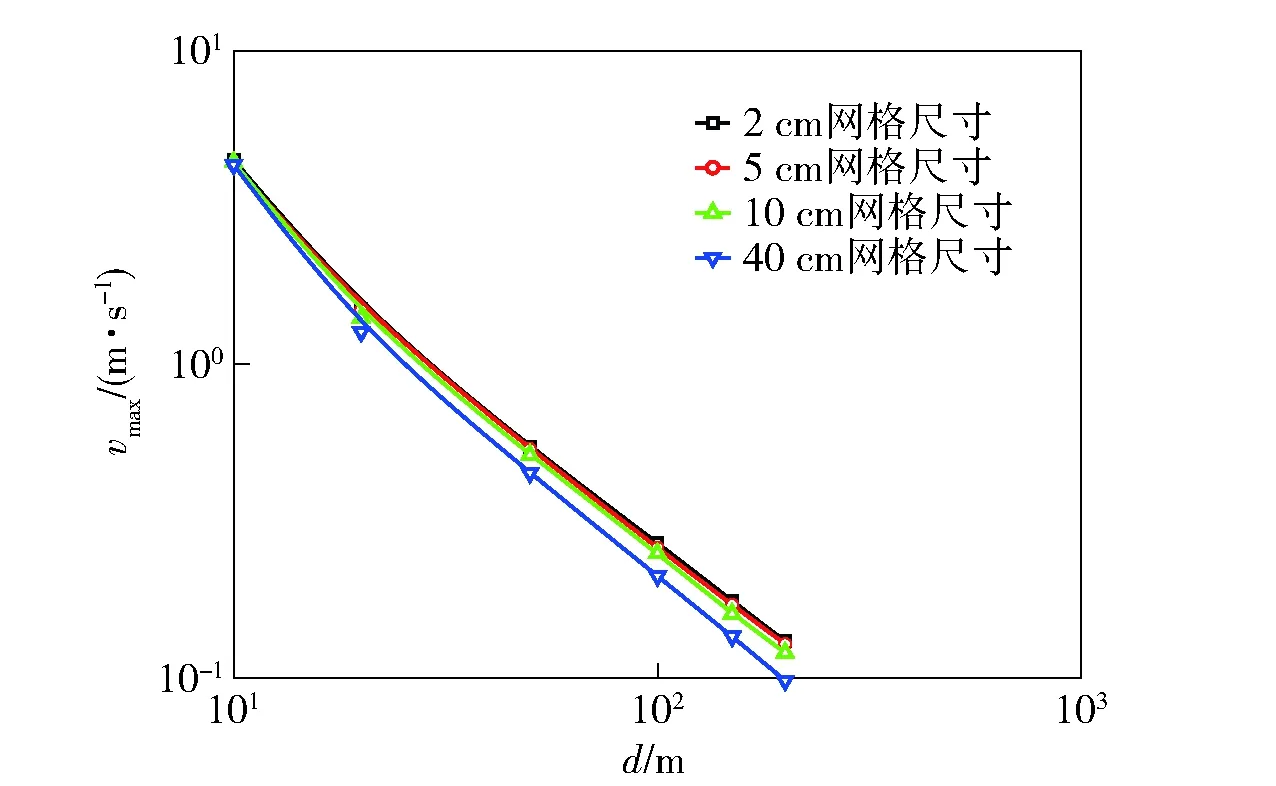
圖10　　　　1 t TNT填實爆炸時的不同網格尺寸自由場速度峰值比較Fig.10　　　　Comparison of free field peak velocities with different mesh size of 1 t TNT tamped explosion

3　網格尺寸敏感性機理分析

從2.3.3節和2.3.4節的分析看到，對于網格敏感量(以壓力p為例)，爆心距越小計算所需的網格尺寸越小，說明在不同的爆心距，物理量對網格的依賴程度不一樣。文獻[16]在研究空氣和水下爆炸時指出，采用同一網格尺寸，在炸藥量較大的情況下可以獲得較為精確的數值結果，而炸藥量較小時與經驗公式計算值偏離較大，即炸藥當量均對數值計算的精度有較大影響——炸藥當量越大，可使用的網格尺寸越大。由此產生疑問：當量對計算網格產生影響的原因是什么？進而還產生疑問，為什么計算相同的物理量在不同爆心距對網格的尺寸要求不同？為此進行了網格尺寸的敏感性機理分析。

首先分析不同炸藥當量產生的差別。從爆炸縮比規律來講，壓力波的作用時間和當量的三分之一次方呈正比。所以爆炸當量越大，產生的爆炸載荷波長越長。而之前的研究結果表明，當一個波長內的網格數目大于等于16個時，基本能夠準確模擬各種物理量。波長越長，相應的模擬所需的網格尺寸也就越大，因此，對于同一網格尺寸，爆炸當量越大，模擬的結果越精確。

為研究物理量在不同爆心距對網格尺寸的依賴程度不同，本文采用1 mm大小的網格尺寸計算得到TNT空中爆炸時不同比例爆心距R的速度波形(如圖11所示)，并對其進行了頻譜分析(如圖12所示)。從圖12看到，隨著爆心距的增大，速度波形中的高頻分量逐漸減小，而低頻分量相對逐漸增多。通常來講，爆炸載荷是由多種頻率的波疊加而成，高頻波波長短，模擬所需的網格尺寸較小，而高頻波衰減較快，隨著爆心距的增加，高頻波成分逐漸減小，低頻波相對成分逐漸增加，因此隨著爆心距的增大，加載波的波長逐漸增加，模擬所需的網格尺寸逐漸增大，因此，隨著爆心距的增大，物理量對網格尺寸的依賴性逐漸降低。

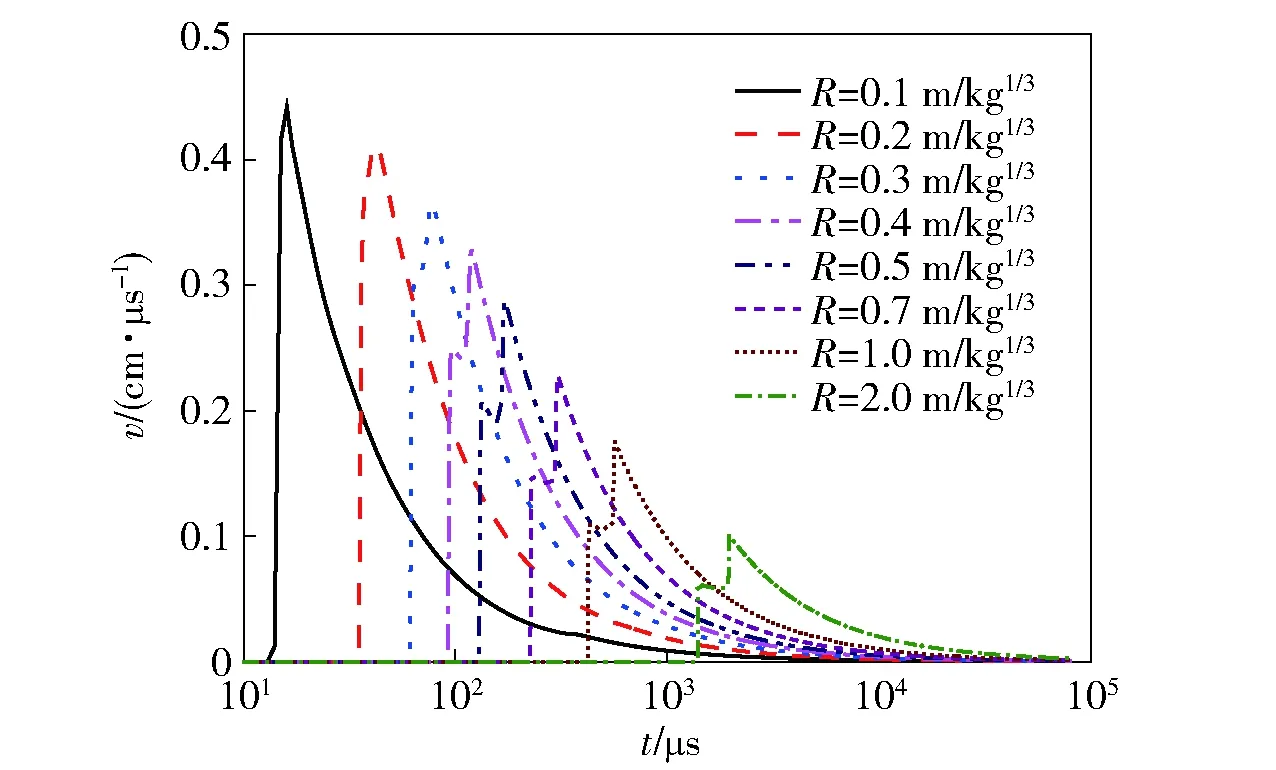
圖11　TNT爆炸時不同比例爆心距的速度波形Fig.11　　　　Velocity waveforms at different scaled distances from explosive source during TNT explosion

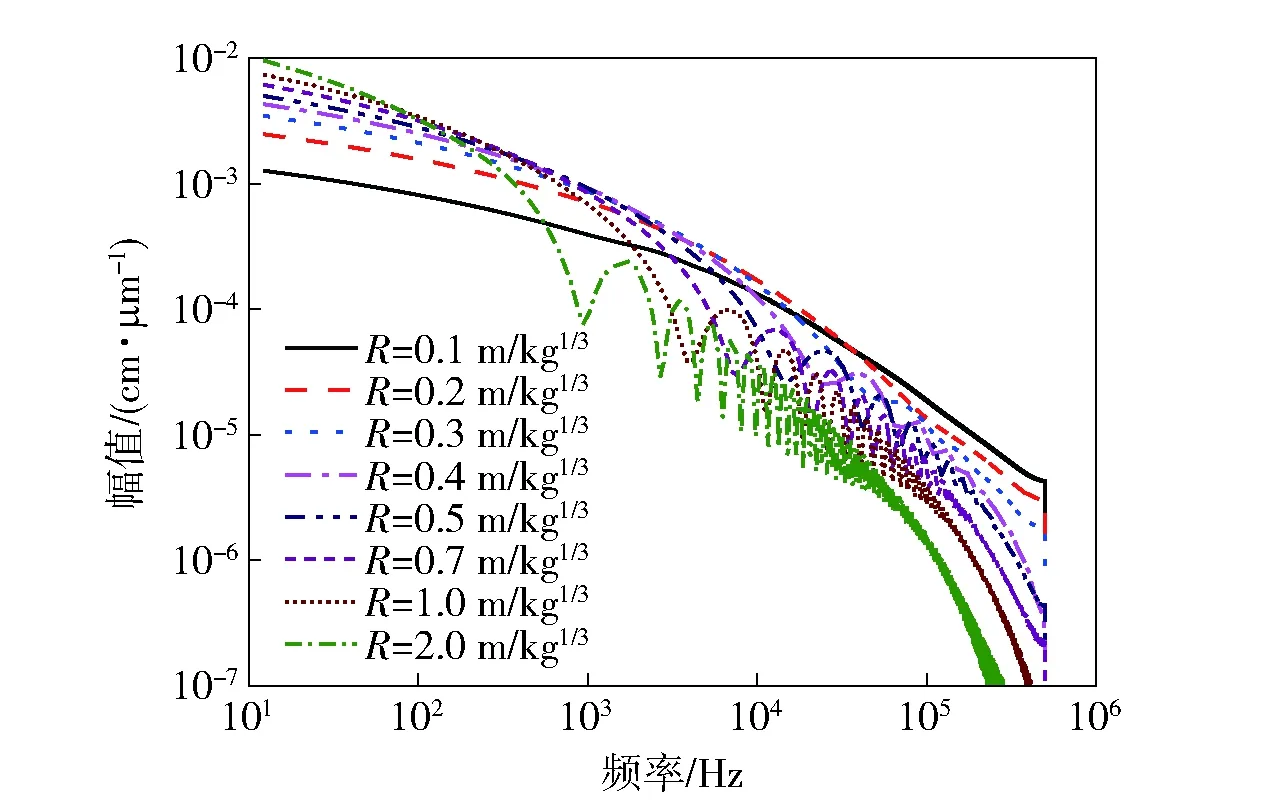
圖12　TNT爆炸時不同比例爆心距的速度波形頻譜分析Fig.12　Spectral analysis of velocity waveforms at different scaled distances from explosive source during TNT explosion

圖13為對某次化爆實驗實測的不同爆心距位置的地震速度波形進行頻譜分析得到的速度譜圖像。從圖中看到，隨著爆心距的增加，振幅峰值前移，說明隨著爆心距的增加高頻分量耗散的較多，低頻份額相對增加。由此導致整體的爆炸波載荷頻率降低，波長增大，從而導致對計算網格尺寸的要求也越來越低，所以會出現隨著爆心距的增加，計算網格尺寸的依賴性降低的現象。從理論上講，根據不同爆心距位置沖擊波的優勢頻率和波長確定合適的網格尺寸更接近問題的本質。然而沖擊波的高頻成分特別豐富，且高頻分量衰減較快，如何確定不同爆心距處的優勢波長尚存在一定困難。雖然目前可以通過網格漸變的劃分方法來定性描述物理量隨著爆心距的增大對網格的依賴性降低的現象，但如何準確地決定網格漸變率仍然有待深入研究。

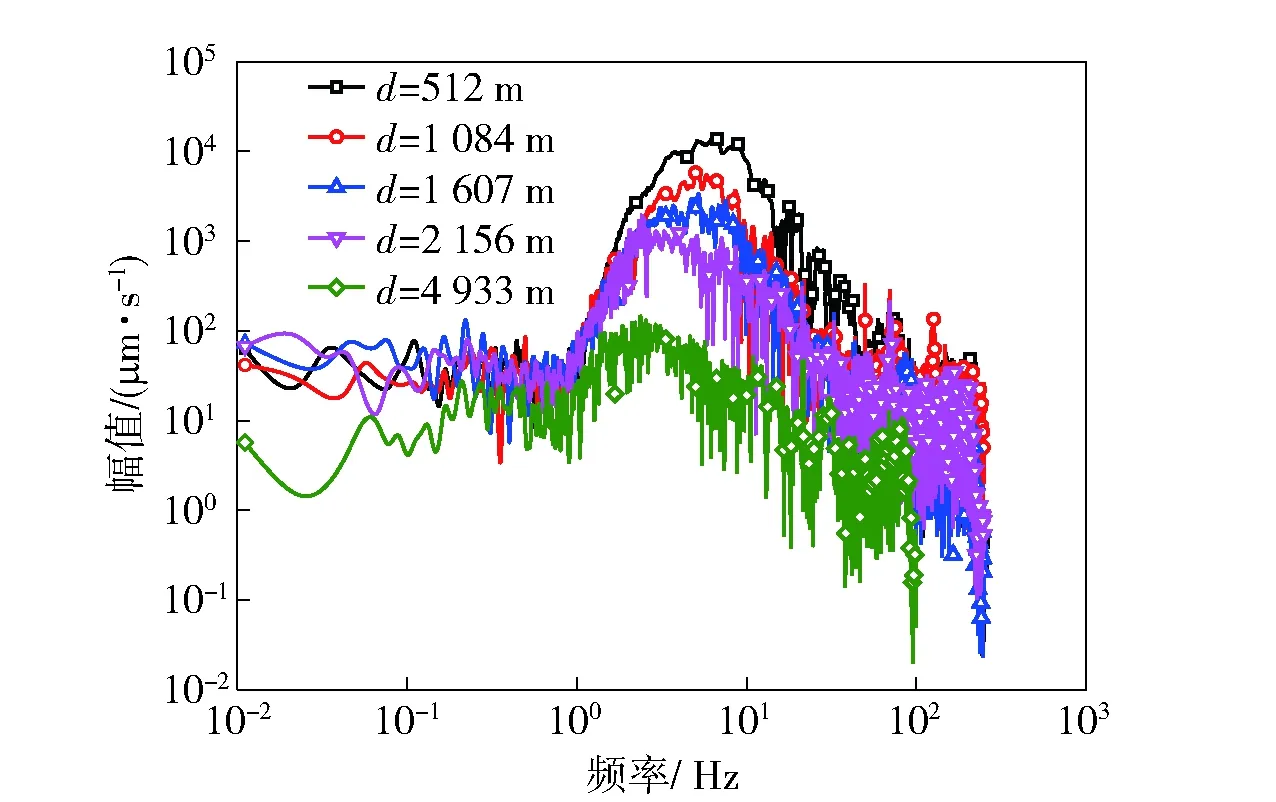
圖13　巖石中爆炸時不同爆心距的速度譜分析Fig.13　Spectral analysis of velocity waveforms at different scaled distances from explosive source during explosion in rock

4　時間步長系數對計算結果的影響

在動力學問題中，時間步長大致等于以聲速通過單元最小特征長度所需的時間，計算中一般采用顯式方法進行求解。在顯式積分方法中，為保證算法的穩定性，積分步長是由最小單元的尺寸控制的。中心差分法是最常用的顯式方法。中心差分法的臨界時間步長取決于單元的特征長度。在小變形問題中，單元的特征長度不變，因此在整個求解過程中可以采用相同的時間積分步長。但在大變形問題中，單元的特征長度不斷減小，因此中心差分法的臨界時間步長也不斷減小，需要采用變步長的中心差分法。LS-DYNA3D程序采用的就是變步長增量解法。對于三維實體單元，其極限時間步長采用如(9)式算法[17]：

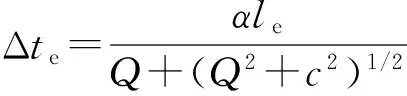
(9)

式中：Q是體黏性系數C0和C1的函數，其表達式為

(10)

圖14　不同時間步長系數計算得到的空腔半徑比較Fig.14　　　　Comparison of calculated cavity radii with different time step coefficients

5　結論

本文通過對巖石中爆炸應力波傳播數值計算中的網格尺寸效應及物理量對網格尺寸的敏感性機理的研究，得到了以下結論：

1) 合適的網格尺寸應根據載荷特征和波傳播介質的屬性來決定。

2) 網格大小對壓力、速度和位移波形的影響較大；當一個波長內的網格個數達到16個以上時，計算得到的壓力峰值、速度峰值和位移峰值等參量基本趨于穩定。

3) 壓力峰值、壓力上升率、速度峰值等參量是網格密度的正相關量；壓力脈寬、波形的振蕩次數、振蕩頻率、波形穩定時間和位移峰值等參量是網格密度的負相關量；而波前到達時間、正壓作用時間、正壓沖量、位移穩態值和爆室內的穩定壓力等參量是網格無關量。

4) 隨著爆心距的增加，物理量對網格尺寸的依賴性降低，其機理是隨著爆心距的增加，載荷中的高頻成分逐漸衰減、載荷的波長變大，模擬所需的網格尺寸變大。

5) 步長系數對計算結果的影響也非常明顯，當時間步長系數取0.05時，位移穩態值趨于收斂值。

本文通過對網格尺寸這一關鍵計算因素對計算結果影響的研究，了解了哪些物理量是計算的確定量，哪些物理量是計算的不確定量；網格尺寸對各種物理量影響規律的獲得，對計算模型的修正及對計算結果的可靠性把握起了很大的提升作用，使大規模的定量計算應用于實際工程問題成為可能。

References)

[1]張雄, 王天舒. 計算動力學[M]. 北京: 清華大學出版社, 2007.

ZHANG Xiong, WANG Tian-shu. Computational dynamics[M]. Beijing: Tsinghua University Press, 2007. (in Chinese)

[2]陸金甫, 關治. 偏微分方程數值解法[M]. 北京:清華大學出版社, 2004.LU Jin-fu, GUAN Zhi. Numerical solution of partial differential equation[M]. Beijing: Tsinghua University Press, 2004. (in Chinese)

[3]李順波, 東兆星, 齊燕軍, 等. 爆炸沖擊波在不同介質中傳播衰減規律的數值模擬[J]. 振動與沖擊, 2009, 28(7):115-117.

LI Shun-bo, DONG Zhao-xing, QI Yan-jun, et al. Numerical simulation for spread decay of blasting shock wave in different media[J]. Journal of Vibration and Shock, 2009, 28(7):115-117.(in Chinese)

[4]胡八一, 柏勁松, 劉大敏, 等. 爆炸容器的工程設計方法及其應用[J]. 壓力容器, 2000, 17(2):39-41.HU Ba-yi, BAI Jin-song, LIU Da-min, et al. The engineering design method of explosion-containment vessel and its application[J]. Pressure Vessel Technology, 2000, 17(2): 39-41. (in Chinese)

[5]Chapman T C. Blast wave simulation using AUTODYN 2D: a parametric study[J]. International Journal of Impact Engineering, 1995, 16(5): 777-787.

[6]胡八一, 李平, 張振宇, 等.爆炸塔內壁特征點的反射壓力數值模擬[J]. 計算力學學報, 2009, 26(4): 573-578.

HU Ba-yi, LI Ping, ZHANG Zhen-yu, et al. Numerical simulation of characteristic points reflective pressure on the inner surface of the explosion chamber[J]. Chinese Journal of Computational Mechanics, 2009, 26(4):573-578.(in Chinese)

[7]楊鑫, 石少卿, 程鵬飛, 等. 爆炸沖擊波在空氣中傳播規律的經驗公式對比及數值模擬[J]. 四川建筑, 2007, 27(5): 71-73.

YANG Xin, SHI Shao-qing, CHENG Peng-fei, et al. Numerical simulation and comparison with empirical formula on the law of shock wave generated by TNT explosions in air[J]. Sichuan Architecture, 2007, 27(5): 71-73.(in Chinese)

[8]雷鳴, 田宙, 張海波, 等. 網格疏密對空中化爆自由場參數計算結果的影響[R]. 西安:西北核技術研究所, 2005.

LEI Ming, TIAN Zhou, ZHANG Hai-bo, et al. Study on the effects of mesh density to the results of freefield parameters about explosion in air[R]. Xi’an:Northwest Institute of Nuclear Technology, 2005.(in Chinese)

[9]姚成寶, 王宏亮, 張柏華, 等. TNT空中爆炸沖擊波傳播數值模擬及數值影響因素分析[J]. 現代應用物理, 2014, 5(1): 39-44.

YAO Cheng-bao, WANG Hong-liang, ZHANG Bai-hua, et al. Numerical simulation of shock wave generated by TNT explosions in infinite air[J]. Modern Applied Physics, 2014, 5(1): 39-44.(in Chinese)

[10]王海兵, 曹淵, 張海波, 等. 5kg TNT當量爆炸容器力學響應數值模擬及參數敏感性分析[C]∥第二屆全國爆炸容器專題研討會論文集. 西安:西北核技術研究所, 2013.

WANG Hai-bing, CAO Yuan, ZHANG Hai-bo, et al. Numerical simulation on dynamic response of 5kg TNT equivalent explosion container and parameters sensitivity analysis[C]∥Proceedings of the Second National Symposium on Explosive Containers. Xi’an: Northwest Institute of Nuclear Technology, 2013. (in Chinese)

[11]Shi Y C, Li Z X, Hao H. Mesh size effect in numerical simulation of blast wave propagation and interaction with structures[J]. Transactions of Tianjin University, 2008, 14(6): 396-402.

[12]梁正召, 王述紅, 唐春安, 等. 非均勻性巖石破裂的網格效應[J]. 巖石力學與工程學報, 2005, 24(增刊1):5108-5112.

LIANG Zheng-zhao, WANG Shu-hong, TANG Chun-an, et al. Mesh effects on failure processes of heterogeneous rocks[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(S1):5108-5112.(in Chinese)

[13]崔煥平, 崔燕平, 王宗敏. 混凝土非線性有限元分析中的網格尺寸效應[J]. 混凝土, 2007(6): 27-29.

CUI Huan-ping, CUI Yan-ping, WANG Zong-min. Mesh size effect in nonlinear finite element analysis of concrete[J]. Concrete, 2007(6): 27-29.(in Chinese)

[14]門建兵, 隋樹元, 蔣建偉, 等. 網格對混凝土侵徹數值模擬的影響[J]. 北京理工大學學報, 2005, 25(8):659-662.

MEN Jian-bing, SUI Shu-yuan, JIANG Jian-wei, et al. Mesh dependency for numerical simulation of concrete penetration[J]. Transactions of Beijing Institute of Technology, 2005, 25(8):659-662.(in Chinese)

[15]Shayanfar M A, Kheyroddin A, Mirza M S. Element size effects in nonlinear analysis of reinforced concrete members[J]. Computers and Structures, 1997, 62(2): 339-352.

[16]張社榮, 李宏璧, 王高輝, 等. 空中和水下爆炸沖擊波數值模擬的網格尺寸效應對比分析[J]. 水利學報, 2015, 46(3):298-306.

ZHANG She-rong, LI Hong-bi, WANG Gao-hui, et al. Comparative analysis of mesh size effects on numerical simulation of shock wave in air blast and underwater explosion[J]. Journal of Hydraulic Engineering, 2015, 46(3):298-306.(in Chinese)

[17]Hallquist J O. LS-DYNA theory manual[M]. Livermore, CA: Livermore Software Technology Corporation, 2006.

Mesh Size Effect and Its Mechanism Research in Numerical Calculation of Rock Dynamics

WANG Hai-bing1,2， ZHANG Hai-bo2， TIAN Zhou2， OU Zhuo-cheng1， ZHOU Gang2

(1.State Key Laboratory of Explosion Science and Technology, Beijing Institute of Technology, Beijing 100081, China; 2.Northwest Institute of Nuclear Technology, Xi’an 710024, Shaanxi, China)

In rock dynamics calculation, the mesh size has an important influence on the reliability of numerically calculated results. A numerical experimental method is used to research the mesh size effect and its sensitivity mechanism in the numerical simulation of propagation of explosion stress wave in rock. The research results show that a proper mesh size should be specified both by the load characteristics and the property of wave propagation medium. When the number of mesh is up to 16 within one load wavelength, the waveforms and peak values of all calculated physical quantities trend to be stable.The relationships between the values of physical quantities and the different mesh densities are also presented. With the increase in distance from explosive source, the sensitivity of physical quantities to mesh size decreases. This is because high-frequency components attenuate gradually, and the wavelength of load becomes longer with the increase in distance from explosive source. The time step coefficient also has a great influence on computational results. When the time step coefficient equals to 0.05, the stable value of displacement tends to converge.

ordnance science and technology; numerical calculation; mesh size; time step; sensitivity mechanism

2016-03-07

國家自然科學基金項目(91330205)

王海兵(1980—)，男， 博士研究生。E-mail: wanghaibing@nint.ac.cn；

歐卓成(1961—)，男，教授，博士生導師。E-mail: zcou@bit.edu.cn

O383+.1

A

1000-1093(2016)10-1828-09

10.3969/j.issn.1000-1093.2016.10.009