數據的集中趨勢與離散程度知識梳理及典型問題

薛飛

數據的集中趨勢與離散程度知識梳理及典型問題

薛飛

《數據的集中趨勢與離散程度》這一章中我們主要學習了體現數據集中趨勢的三種“數”——平均數、中位數和眾數以及體現數據離散程度的兩種“差”——極差與方差.

平均數分“算術平均數”與“加權平均數”，我們重點理解加權平均數.加權平均數重在理解什么是“權”.課本中是這樣定義“權”的：一組數據的平均數，不僅與這組數據中各個數據的值有關，而且與各個數據的“重要程度”有關.我們把衡量各個數據的“重要程度”的數值叫做“權”.

例1學校食堂午餐供應3元、4元和5元三種價格的盒飯，根據食堂某月銷售午餐盒飯的統計圖，計算該月食堂銷售午餐盒飯的平均價格.

【分析】這個題目給出的兩組數據分別是：①午餐盒飯的價格為3元、4元和5元；②不同價格的盒飯所占的比例.題目最后要求的是午餐盒飯的平均價格，也就是說第①組數據是題目研究的數據對象，第②組數據中盒飯所占的比例是“權”.

解：該月食堂銷售午餐盒飯的平均價格為

答：該月食堂銷售的午餐盒飯的平均價格為3.9元.

求中位數的一般步驟：①把數據從小到大排列；②若該數據含有奇數個數，位于中間位置的數是中位數，若該數據含有偶數個數，位于中間位置的兩個數的平均數就是中位數.

例2有奇數個數據10，20，80，40，30，90，50，40，50，40，60，求這一組數據的中位數.

【分析】把這組數據按從小到大的順序排列10、20、30、40、40、40、50、50、60、80、90，該數據含有奇數個數，位于中間位置的數是中位數，所以該組數據的中位數為40.

例3一組數據分別為1，2，8，4，3，9，5，4，5，6，求這組數據的中位數.

【分析】首先把這組數據按從小到大的順序排列1，2，3，4，4，5，5，6，8，9，該組數據共有10個，所以第5個和第6個數據的平均數4.5為中位數.

【點評】中位數的求法一定要注意先排序，后根據總數的奇偶來找出中位數，從例3中可以看出中位數4.5并不是原始數據，所以中位數也不一定是原始數據中的一個.

一組數據中出現次數最多的數據叫做這組數據的眾數.眾數可以沒有，可以只有一個，也可以有多個.

例3一次數學測驗后，老師將全班40名學生的成績整理后繪制成頻數分布直方圖，判斷下列命題正確的是.

①全班成績的中位數在84～96這一組；②全班成績的眾數在84～96這一組.

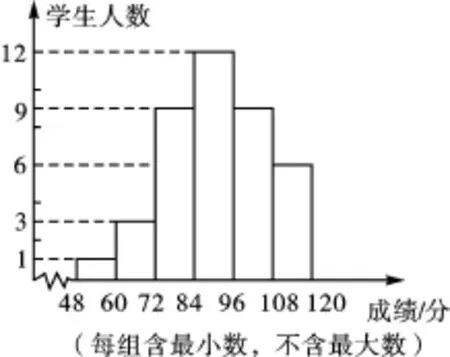
【分析】命題①正確，命題②在判斷眾數的時候往往會掉入陷阱，看到84～96這一組最高，所以眾數確定就在這一組.舉個反例便知錯在哪里：84～96之間一共是12人，其中84分，85分，86分，87分各3人，而72～84這一組中的9人分數都是80分，顯然全班成績的眾數不在84～96這一組，所以這題正確的只有命題①.

極差概念簡單，通俗地說就是最大數據與最小數據的差，反映了一組數據的變化范圍.

例4某位射擊運動員射擊5次命中的環數分別為6，7，9，10，8，求極差.

【分析】找出最大值和最小值即可，最大值為10環，最小值為6環，所以極差為10-6=4.

描述一組數據的離散程度還有方差，方差的計算公式：

例6為了從甲、乙兩人中選拔一人參加射擊比賽，現對他們的射擊成績進行了測試，5次打靶命中的環數如下：甲：8，7，10，7，8；乙：9，5，10，9，7.

（1）將下表填寫完整：

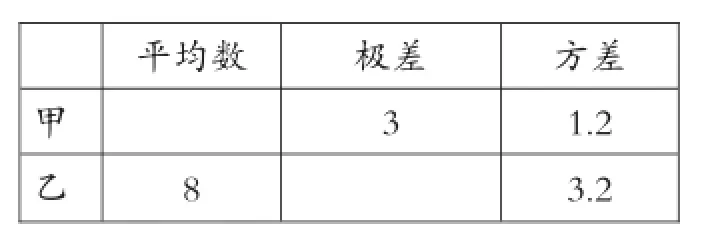
平均數甲乙方差1 . 2 3 . 2極差3 8

（2）根據以上信息，若你是教練，選擇誰參加射擊比賽，理由是什么？

（3）若乙再射擊一次，命中8環，則乙這6次射擊成績的方差會__________.（填變大或變小或不變）

【分析】通過計算得出甲乙兩人的平均數都是8環，但是甲的極差比乙小，更重要的是甲的方差也比乙小，方差越小越穩定，所以教練會選擇發揮較為穩定的甲參加比賽.第（3）問的解決需要用到方差的計算公式，原來5次射擊的方差是這樣計算的

不難發現分子雖然增加了一項，但是分子的值并沒有變化，但是分母卻變大了，所以分子不變，分母變大，最終方差變小.

（作者單位：江蘇省常州市武進區湖塘實驗中學）