基于隨機(jī)網(wǎng)絡(luò)演算的TTE網(wǎng)絡(luò)時(shí)延分析
趙露茜, 李峭, 林晚晴, 熊華鋼
北京航空航天大學(xué) 電子信息工程學(xué)院, 北京 100083
?
基于隨機(jī)網(wǎng)絡(luò)演算的TTE網(wǎng)絡(luò)時(shí)延分析
趙露茜, 李峭*, 林晚晴, 熊華鋼
北京航空航天大學(xué) 電子信息工程學(xué)院, 北京100083
時(shí)間觸發(fā)以太網(wǎng)(TTE)是一種新穎的混合型時(shí)間觸發(fā)和事件觸發(fā)的通信網(wǎng)絡(luò),通過(guò)引入時(shí)間觸發(fā)(TT)流量,增強(qiáng)了航空電子全雙工(AFDX)交換式以太網(wǎng)的確定性。雖然TT流量具有完全的時(shí)間確定性,但是與AFDX中虛擬鏈路(VL)兼容的速率約束(RC)流量仍具有一定非確定性。傳統(tǒng)用于AFDX網(wǎng)絡(luò)實(shí)時(shí)性能分析的方法在考慮TT流量固定分區(qū)調(diào)度時(shí)隙的影響下已不再適用,為了保障RC流量的實(shí)時(shí)性能,分別提出了基于確定性網(wǎng)絡(luò)演算和隨機(jī)網(wǎng)絡(luò)演算兩種延遲分析模型。在確定性網(wǎng)絡(luò)演算下,通過(guò)構(gòu)造TT流量的聚合到達(dá)曲線和RC流量的服務(wù)曲線以得到RC的確定性延遲上界;在隨機(jī)網(wǎng)絡(luò)演算下,通過(guò)切諾夫(Chernoff)邊界定理構(gòu)造RC流量的兩狀態(tài)伯努利分布模型,得到概率保證下的延遲上界。對(duì)比實(shí)驗(yàn)結(jié)果表明:隨機(jī)網(wǎng)絡(luò)演算模型可以有效減小確定性網(wǎng)絡(luò)演算模型對(duì)RC流量性能分析的悲觀性,同時(shí)從一定程度上驗(yàn)證了兩種理論分析模型的正確性。
航空電子; 時(shí)間觸發(fā)以太網(wǎng); 性能分析; 網(wǎng)絡(luò)演算; 隨機(jī)網(wǎng)絡(luò)演算; 延遲上界
時(shí)間觸發(fā)以太網(wǎng)[1-3](TTE)是一種改進(jìn)時(shí)間關(guān)鍵性和安全關(guān)鍵性的應(yīng)用于航空航天領(lǐng)域的網(wǎng)絡(luò),它通過(guò)離線設(shè)計(jì)時(shí)間觸發(fā)(TT)流量的調(diào)度時(shí)隙,部分消除了航空電子全雙工(AFDX)交換式以太網(wǎng)[4]的非確定性。
TTE網(wǎng)絡(luò)為了支持不同實(shí)時(shí)性和安全性需求的應(yīng)用,將流量劃分為3類[5],TT流量、速率約束(RC)流量和盡力傳(BE)流量。TT流量用于對(duì)延遲、抖動(dòng)等確定性要求高的應(yīng)用,RC流量用于對(duì)確定性要求稍弱一些的應(yīng)用,它與AFDX中虛擬鏈路(VL)的傳輸模式兼容,BE流量為傳統(tǒng)以太網(wǎng)通信方式,具有最低優(yōu)先級(jí)且無(wú)需服務(wù)質(zhì)量(QoS)保證。
目前國(guó)內(nèi)外對(duì)于TTE網(wǎng)絡(luò)研究主要集中在網(wǎng)絡(luò)的配置優(yōu)化以及TT調(diào)度表的離線設(shè)計(jì)。Tamas-Selicean等[6-7]在考慮最小化RC延遲的情況下,綜合優(yōu)化TTE網(wǎng)絡(luò)的虛擬鏈路幀分配、路由分配等配置方法;文獻(xiàn)[8]針對(duì)分區(qū)調(diào)度表提出了一種基于時(shí)間窗檢測(cè)的TT與RC流量的轉(zhuǎn)換策略。此外,Steiner[9-10]提出一種基于可滿足性模理論(SMT)解析器的TT調(diào)度表生成方法,通過(guò)給定的約束集求得滿足條件的可行解;Tamas-Selicean和Steiner[11-12]基于Tabu搜索離線設(shè)計(jì)了TT調(diào)度表,并在TT調(diào)度的前提條件下對(duì)RC流量時(shí)序關(guān)系進(jìn)行分析。文獻(xiàn)[13]引入一種分區(qū)的調(diào)度機(jī)制,將每個(gè)基本周期劃分為專門用于發(fā)送TT流量和RC/BE流量的兩段。
目前對(duì)于RC流量確定性分析的研究還比較少,由于TT幀固定調(diào)度時(shí)隙的影響,傳統(tǒng)用于AFDX網(wǎng)絡(luò)實(shí)時(shí)性能分析的方法[14-18]已不再適用。文獻(xiàn)[19]中針對(duì)TT流量的孔隙調(diào)度模型,提出了確定性網(wǎng)絡(luò)演算對(duì)RC流量的分析方法,然而由于最壞情況為小概率事件,上述分析方法下的最壞延遲估計(jì)具有較大的悲觀性。
本文針對(duì)TT流量的分區(qū)調(diào)度模型,提出基于確定性網(wǎng)絡(luò)演算的RC性能分析模型,同時(shí)為了改善確定性網(wǎng)絡(luò)演算帶來(lái)的悲觀性,本文還基于隨機(jī)網(wǎng)絡(luò)演算對(duì)RC流量進(jìn)行分析建模,分別得到RC流量的確定性上界和概率保證下的上界。實(shí)驗(yàn)對(duì)兩種模型的估計(jì)結(jié)果進(jìn)行了比較,并對(duì)兩種建模方法進(jìn)行了仿真驗(yàn)證。
1 TTE網(wǎng)絡(luò)分區(qū)調(diào)度模型
TT調(diào)度模型并不由TTE協(xié)議提供,而是靈活地提供給設(shè)計(jì)者。文獻(xiàn)[13]提出一種分區(qū)模式的TT調(diào)度表,如圖1所示。TT流量的傳輸在時(shí)域上獨(dú)立于RC和BE流量,同時(shí)在帶寬上隔離RC和BE流量,RC流量獲得配置帶寬,BE流量利用空閑帶寬盡最大可能傳送數(shù)據(jù)幀。

圖1 分區(qū)時(shí)間觸發(fā)(TT)調(diào)度表Fig.1 Partitioned time-triggered (TT) schedule
每個(gè)節(jié)點(diǎn)(終端/交換機(jī))端口有一張分區(qū)的TT調(diào)度表,圖2為一張對(duì)應(yīng)于實(shí)驗(yàn)網(wǎng)絡(luò)拓?fù)浣粨Q機(jī)S1端口1的調(diào)度表示意圖。由于各TT流量的數(shù)據(jù)幀嚴(yán)格按照周期性(2的冪次方)從終端發(fā)送,各調(diào)度表的時(shí)間軸以矩陣周期(Matrix Cycle, MC)為單位周期性的循環(huán),一個(gè)矩陣周期的長(zhǎng)度lMC定義為網(wǎng)絡(luò)中所有TT流量周期的最小公倍數(shù):
(1)
此外,一個(gè)矩陣周期又劃分為若干個(gè)基本周期(Basic Cycle, BC),基本周期的長(zhǎng)度lBC定義為網(wǎng)絡(luò)中所有TT流量的最小可能周期:
(2)
那么一個(gè)矩陣周期包括nBC個(gè)基本周期:
nBC=lMC/lBC
(3)
每個(gè)基本周期被劃分為兩段,前一段專門用于發(fā)送TT數(shù)據(jù)幀,后一段專門用于發(fā)送RC和BE數(shù)據(jù)幀。根據(jù)左端緊縮原則,將TT幀均勻間隔的縱向分布放置在nBC個(gè)基本周期內(nèi)。

圖2 基本周期和矩陣周期Fig.2 Basic cycle and matrix cycle
TT與RC流量的傳輸模式[5]分為3種:搶占(Preemption)模式、及時(shí)阻斷(Timely Block)模式和洗牌(Shuffling)模式,如圖 3所示。搶占模式表示若RC幀在傳輸?shù)倪^(guò)程中遇到TT幀,則RC幀被終止傳送,直至TT幀傳輸完畢并再次有空閑時(shí)段時(shí),RC幀被繼續(xù)發(fā)送。及時(shí)阻斷模式表示RC幀在傳輸前需要預(yù)判距離下一個(gè)相鄰的TT幀之間是否有足夠的空閑時(shí)段供其完整傳輸,若沒(méi)有RC幀將被延遲傳送。洗牌模式表示RC幀將推遲TT幀預(yù)先安排的傳輸時(shí)隙。考慮到及時(shí)阻斷模式在TTE網(wǎng)絡(luò)中應(yīng)用更廣泛,本文主要研究在這種傳輸模式下的網(wǎng)絡(luò)性能。

圖3 TT與速率約束(RC)流量的傳輸模式Fig.3 Transmission modes between TT and rate-constrained (RC) flow
2 基于確定性網(wǎng)絡(luò)演算的RC延遲分析
2.1確定性網(wǎng)絡(luò)演算
網(wǎng)絡(luò)演算[20]是一種網(wǎng)絡(luò)性能分析方法,可以用于計(jì)算網(wǎng)絡(luò)流量的延遲上界。網(wǎng)絡(luò)演算主要概念包括到達(dá)曲線、服務(wù)曲線、最小加代數(shù)下的卷積和反卷積運(yùn)算。


(4)

(5)
式中:σ為最大突發(fā)度;ρ為流量平均速率上界。

(6)
(7)
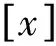
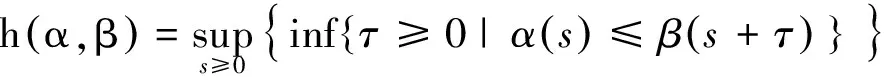
(8)
2.2RC流量確定性延遲上界分析
在TTE網(wǎng)絡(luò)中,RC流量與AFDX的虛擬鏈路相兼容,每條流量τRCi在源終端受到最大幀長(zhǎng)SRCi,max以及兩個(gè)相鄰幀之間的最小幀間隔BAGRCi的約束。因此在源終端τRCi的到達(dá)曲線可以表示為
(9)
然而由于在當(dāng)前節(jié)點(diǎn)端口排隊(duì)的原因,τRCi的輸出到達(dá)曲線即下一節(jié)點(diǎn)端口的輸入到達(dá)曲線的突發(fā)度有所增加:
(10)

假設(shè)τRCi在沿其路徑上的第h個(gè)節(jié)點(diǎn)端口中還有其他n-1條已知輸入到達(dá)曲線的RC流量,它們的聚合到達(dá)曲線可以表示為
(11)
RC聚合流量的服務(wù)取決于鏈路物理速率C以及調(diào)度表的占空比,更具體來(lái)說(shuō)取決于在一個(gè)基本周期內(nèi)配置TT時(shí)段的長(zhǎng)度lTT,以及由于及時(shí)阻斷模式下造成最多一個(gè)RC幀長(zhǎng)度的阻塞時(shí)延。在最壞情況下,一個(gè)基本周期內(nèi)RC流量的延遲為
l1=lTT+SRC,max/C
(12)
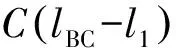
(13)
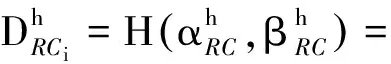
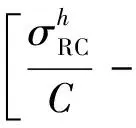
(14)

圖4 RC聚合流量的服務(wù)曲線Fig.4 Service curve of aggregate RC flows

圖5 最大水平距離Fig.5 Maximum horizontal deviation
3 基于隨機(jī)網(wǎng)絡(luò)演算的RC延遲分析
3.1隨機(jī)網(wǎng)絡(luò)演算
雖然確定性網(wǎng)絡(luò)演算給出RC流量的延遲上界,但是由于在考慮聚合流量的情況下,這種最壞情況發(fā)生的可能性非常小。Chang等[21]在2001年提出一種基于確定性流量和確定性服務(wù)的統(tǒng)計(jì)上界模型。

Chang的隨機(jī)網(wǎng)絡(luò)演算的流量模型需要滿足以下條件:
1) τ1,τ2,…,τn為相互獨(dú)立的流量。
2) τ1,τ2,…,τn為平穩(wěn)的流量。




(15)
3.2RC流量概率性延遲上界分析

(16)
穩(wěn)定性條件確保一定存在τ<∞,作為忙時(shí)段的上界:
(17)

(18)
(19)
引理1(切諾夫邊界[22])一個(gè)隨機(jī)變量X,對(duì)于任意常量x和所有θ≥0,都有
(20)
式中:EeθX稱為隨機(jī)變量X的矩量母函數(shù)[22]。
即
(21)
式中:Λ(θ)為累積量母函數(shù),它是矩量母函數(shù)上界的自然對(duì)數(shù)。
(22)
式中:
(23)
證明:根據(jù)h節(jié)點(diǎn)端口積壓式(17)和切諾夫邊界引理(引理 1),對(duì)于?θ≥0有
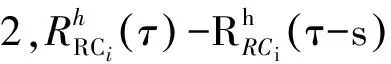
(24)
式中:
那么
(25)

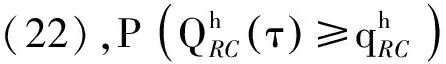
(26)
另外,根據(jù)端口RC聚合流量概率保證下的積壓上界可以求得其概率保證下的延遲上界為

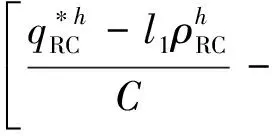
(27)
4 實(shí)驗(yàn)分析

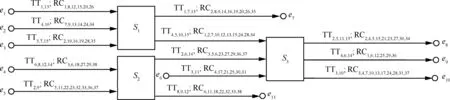
圖6 時(shí)間觸發(fā)以太網(wǎng)(TTE)網(wǎng)絡(luò)架構(gòu)Fig.6 Time-triggered ethermet (TTE) network architecture

Table 1 Periods of TT flows ms

表2 RC流量帶寬分配間隔(BAGs)
基于VC++開發(fā)平臺(tái),首先實(shí)現(xiàn)了確定性網(wǎng)絡(luò)演算對(duì)RC流量延遲上界估計(jì)的算法,再以其得到的各節(jié)點(diǎn)端口前的流量突發(fā)度和積壓上界作為輸入量,開發(fā)隨機(jī)性網(wǎng)絡(luò)演算對(duì)RC流量概率延遲估計(jì)的算法(保證概率為10-5)。由兩種方法計(jì)算得到的各條RC流量的端到端延遲如圖7 所示,圖中橫軸表示順序排列的RC流量(RC1, RC2(e7), RC2(e8), RC3, …);此外,表3給出部分RC流量延遲的數(shù)值結(jié)果。根據(jù)運(yùn)行結(jié)果分析可知,在當(dāng)前TTE網(wǎng)絡(luò)配置下,隨機(jī)網(wǎng)絡(luò)演算在概率保證下對(duì)RC流量延遲上界的估計(jì)比確定性網(wǎng)絡(luò)演算對(duì)RC流量延遲上界的估計(jì)減少了26.58%。在該算例中,隨機(jī)網(wǎng)絡(luò)演算在TTE網(wǎng)絡(luò)中的應(yīng)用減少了確定性網(wǎng)絡(luò)演算的悲觀性。
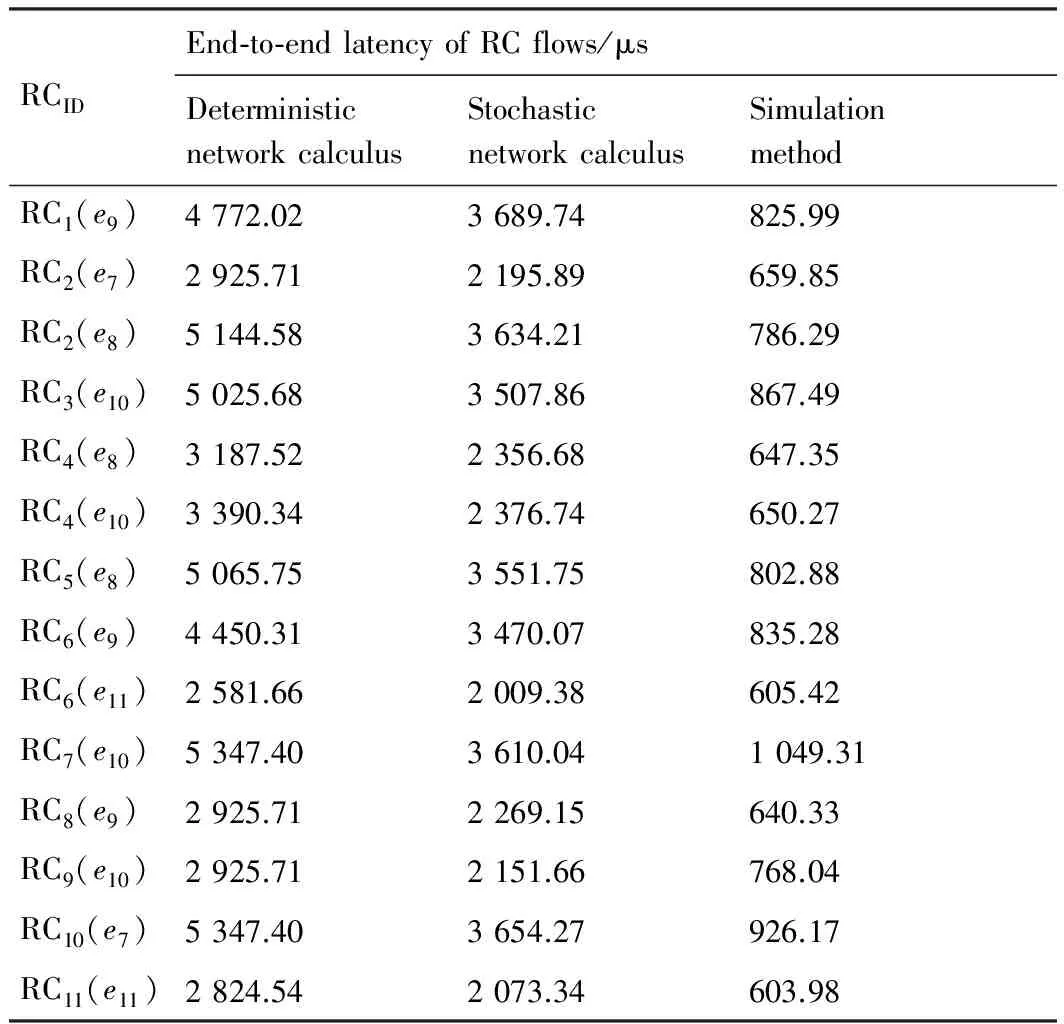
表3 部分RC流量延遲比較
除此之外,為了驗(yàn)證兩種理論算法的正確性,通過(guò)仿真的方法對(duì)TTE網(wǎng)絡(luò)中RC延遲進(jìn)行統(tǒng)計(jì),最大的仿真延遲結(jié)果如表3第4欄所示。從圖7中可以清楚的看出,最大仿真延遲均未超過(guò)理論計(jì)算值,一方面,這是由于理論上界在極限情況下得到,在仿真情況下很難發(fā)生;另一方面,由于仿真結(jié)果小于或等于實(shí)際最壞延遲,因此從一定程度上驗(yàn)證了兩種理論估計(jì)結(jié)果的正確性。
下面比較在不同TT流量占用率的情況下,隨機(jī)網(wǎng)絡(luò)演算對(duì)確定性網(wǎng)絡(luò)演算的改進(jìn)情況。假設(shè)RC流量條數(shù)和路徑均不變,通過(guò)增加TT流量的條數(shù)來(lái)增大TT流量的帶寬占用率。圖8 給出了TT帶寬占用率分別為6%、10%和20%的情況下,隨機(jī)網(wǎng)絡(luò)演算(保證概率為10-5)相對(duì)于確定性網(wǎng)絡(luò)演算對(duì)RC延遲估計(jì)結(jié)果減小的比例。可以看出,隨著TT流量占用率的增大,RC調(diào)度的隨機(jī)因素隨之降低,因而兩種理論方法對(duì)于RC延遲的估算結(jié)果的差異性明顯降低。

圖7 RC流量延遲比較Fig.7 Latency comparison of RC flows

圖8 不同TT占用率下兩種理論方法的差異Fig.8 Difference between two theoretical methods under different TT occupancy rate
5 結(jié) 論
針對(duì)TTE交換網(wǎng)絡(luò),本文提出了兩種基于分區(qū)調(diào)度策略下RC流量延遲的分析方法。
1) 確定性網(wǎng)絡(luò)演算模型給出RC流量確定的延遲上界,然而具有較大的悲觀性。隨機(jī)網(wǎng)絡(luò)演算模型給出概率保證下的RC流量的延遲上界,在一定程度上改善了這種悲觀性。
2) 隨著TT流量帶寬占用率的增加,隨機(jī)網(wǎng)絡(luò)演算模型對(duì)確定性網(wǎng)絡(luò)演算模型的悲觀性優(yōu)化隨之降低。
3) 分區(qū)調(diào)度是其中一種TT調(diào)度策略,下一步,應(yīng)將隨機(jī)網(wǎng)絡(luò)演算應(yīng)用于基于孔隙調(diào)度策略下的TTE網(wǎng)絡(luò)中RC流量的概率延遲上界分析。
[1]SAE. Time-triggered ethernet: AS6802[S]. Warrendale, PA: SAE International, 2011.
[2]KOPETZ H, GRUNSTEIDL G. The time-triggered ethernet (TTE) design[C]//8th IEEE International Symposium on Object Oriented Real-Time Distributed Computing. Piscataway, NJ: IEEE Press, 2005: 22-33.
[3]KOPETZ H. Real-time systems: Design principles for distributed embedded applications[M]. Berlin: Springer, 2011: 167-188.
[4]ARINC. ARINC Specification 664P7: Aircraft data network, Part 7: Avionics full-duplex switched Ethernet network[S]. New York: Aeronautical Radio Inc., 2009.
[5]STEINER W, BAUER G, HALL B, et al. TTEthernet dataflow concept[C]//8th IEEE International Symposium on Network Computing and Applications. Piscataway, NJ: IEEE Press, 2009: 319-322.
[6]TAMAS-SELICEAN D. Design of mixed-criticality applications on distributed real-time systems[D]. Denmark: Technical University of Denmark, 2014: 86-98.
[7]TAMAS-SELICEAN D, POP P, STEINER W. Design optimization of TTEthernet-based distributed real-time systems[J]. Real-Time Systems, 2015, 51(1): 1-35.
[8]易娟, 熊華鋼, 何峰, 等. TTE網(wǎng)絡(luò)流量轉(zhuǎn)換策略及其延時(shí)性能保障調(diào)度算法研究[J]. 航空學(xué)報(bào), 2014, 35(4): 1071-1078.
YI J, XIONG H G, HE F, et al. Research on traffic classes transformation strategy and real-time guarantee scheduling algorithm in TTEthernet[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(4): 1071-1078 (in Chinese).
[9]STEINER W. An evaluation of SMT-based schedule synthesis for time-triggered multi-hop networks[C]//IEEE 31st Real-Time Systems Symposium (RTSS). Piscataway, NJ: IEEE Press, 2010: 375-384.
[10]STEINER W. Synthesis of static communication schedules for mixed-criticality systems[C]//14th IEEE International Symposium on Object/Component/Service-Oriented Real-Time Distributed Computing Work-shops. Piscataway, NJ: IEEE Press, 2011: 11-18.
[11]TAMAS-SELICEAN D, POP P, STEINER W. Synthesis of communication schedules for TTEthernet-based mixed-criticality systems[C]//Proceedings of the 8th IEEE/ACM/IFIP International Conference on Hard-ware/Software Codesign and System Synthesis. New York: ACM Press, 2012: 473-482.
[12]TAMAS-SELICEAN D, POP P, STEINER W. Timing analysis of rate constrained traffic for the TTEthernet communication protocol[C]//Proceedings of the 18th IEEE International Symposium on Real-Time Distributed Computing. Piscataway, NJ: IEEE Press, 2015: 119-126.
[13]劉晚春, 李峭, 何峰, 等. 時(shí)間觸發(fā)以太網(wǎng)同步及調(diào)度機(jī)制的研究[J]. 航空計(jì)算技術(shù), 2011, 41(4): 122-127.
LIU W C, LI Q, HE F, et al. Research on time-triggered Ethernet synchronization and scheduling mechanism [J]. Aeronautical Computing Technique, 2011, 41(4): 122-127 (in Chinese).
[14]FRANCES F, FRABOUL C, GRIEU J. Using network calculus to optimize the AFDX network[C]//3rd European Congress ERTS Embedded Real-time Software. Toulouse, France: OATAO Press, 2006: 1-8.
[15]BOYER M. Half-modeling of shaping in FIFO net with network calculus[C]//18th International Conference on Real-Time and Network Systems, 2010: 59-68.
[16]SCHARBARG J L, RIDOUARD F, FRABOUL C. A probabilistic analysis of end-to-end delays on an AFDX avionic net-work[J]. IEEE Transactions on Industrial Informatics, 2009, 5(1): 28-49.
[17]RIDOUARD F, SCHARBARG J L, FRABOUL C. Probabilistic upper bounds for heterogeneous flows using a static priority queueing on an AFDX network[C]//IEEE International Conference on Emerging Technologies and Factory Automation. Piscataway, NJ: IEEE Press, 2008: 1220-1227.
[18]ADNAN M, SCHARBARG J L, ERMONT J, et al. Model for worst case delay analysis of an AFDX network using timed automata[C]//IEEE Conference on Emerging Technologies and Factory Automation. Piscataway, NJ: IEEE Press, 2010: 1-4.
[19]ZHAO L X, XIONG H G, ZHENG Z, et al. Improving worst case latency analysis for rate-constrained traffic in the time-triggered Ethernet network[J]. IEEE Communications Letters, 2014, 18(11): 1927-1930.
[20]LE BOUDEC J Y, THIRAN P. Network calculus: A theory of deterministic queuing systems for the internet [M]. Berlin: Springer, 2001: 3-59.
[21]CHANG C S, CHIU Y M, SONG W T. On the performance of multiplexing independent regulated inputs [C]//ACM SIGMETRICS International Conference on Measurement and Modeling of Computer Systems. New York: ACM Press, 2001: 184-193.
[22]FIDLER M. An end-to-end probabilistic network calculus with moment generating functions[C]//14th IEEE International Workshop on Quality of Service. Piscataway, NJ: IEEE Press, 2006: 261-270.
趙露茜女, 博士研究生。主要研究方向: 實(shí)時(shí)網(wǎng)絡(luò)的性能分析方法。
E-mail: zhaoluxi@buaa.edu.cn
李峭男, 博士, 講師。主要研究方向: 實(shí)時(shí)通信、 性能評(píng)價(jià)。
Tel.: 010-82338894
E-mail: avionics@buaa.edu.cn
林晚晴女, 碩士研究生。主要研究方向: 高速交換網(wǎng)絡(luò)結(jié)構(gòu)與調(diào)度算法。
E-mail: LWQ_1991@buaa.edu.cn
熊華鋼男, 博士, 教授, 博士生導(dǎo)師。主要研究方向: 通信網(wǎng)絡(luò)理論與技術(shù)、航空電子信息綜合和超寬帶通信。
E-mail: hgxiong@buaa.edu.cn
Stochastic network calculus for analysis of latency onTTEthernet network
ZHAO Luxi, LI Qiao*, LIN Wanqing, XIONG Huagang
School of Electronic and Information Engineering, Beihang University, Beijing100083, China
Time-triggered Ethernet (TTE) is a novel hybrid communication network with time-triggered and event-triggered messages. The determinacy of avionics full duplex (AFDX) switched Ethernet is improved by introducing the time-trigger (TT) flow. Even though TT flow has full time certainty, rate-constraint (RC) flow which is compatible with the virtual link (VL) in the AFDX network is still uncertain. Since the influence of fixed schedule slots of TT flow, traditional performance analysis methods used in the AFDX network are not suitable for the. In order to guarantee the real-time performance of RC flow, we propose two latency analysis models respectively based on the deterministic network calculus and stochastic network calculus. Under the deterministic network calculus, the latency upper bounds of RC flow are obtained by constructing the aggregate arrival curve of TT flow and service curve for RC flow. Under the stochastic network calculus, we compute the probabilistic upper bounds for RC flow by constructing two states Bernoulli distribution models for RC flow through Chernoff bound. Comparison results show that stochastic network calculus reduces the pessimism of deterministic network calculus on the performance analysis of RC flow. In addition, simulation results verify the correctness of two theoretical methods in some degree.
avionics; time-triggered Ethernet; performance analysis; network calculus; stochastic network calculus; latency upper bound
2015-07-08; Revised: 2015-09-06; Accepted: 2015-11-13; Published online: 2015-11-2314:29
s: National Natural Science Foundation of China (61301086); the Fundamental Research Funds for the Central Universities (YWF-14-DZXY-018, YWF-14-DZXY-023)
. Tel.: 010-82338894E-mail: avionics@buaa.edu.cn
2015-07-08; 退修日期: 2015-09-06; 錄用日期: 2015-11-13;
時(shí)間: 2015-11-2314:29
www.cnki.net/kcms/detail/11.1929.V.20151123.1429.006.html
國(guó)家自然科學(xué)基金 (61301086); 中央高校基本科研業(yè)務(wù)費(fèi)專項(xiàng)資金 (YWF-14-DZXY-018, YWF-14-DZXY-023)
.Tel.: 010-82338894E-mail: avionics@buaa.edu.cn
10.7527/S1000-6893.2015.0305
V247; TP393
A
1000-6893(2016)06-1953-09
引用格式: 趙露茜, 李峭, 林晚晴, 等. 基于隨機(jī)網(wǎng)絡(luò)演算的TTE網(wǎng)絡(luò)時(shí)延分析[J]. 航空學(xué)報(bào), 2016, 37(6): 1953-1962. ZHAO L X, LI Q, LIN W Q, et al. Stochastic network calculus for analysis of latency on TTEthernet network[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(6): 1953-1962.
http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn
URL: www.cnki.net/kcms/detail/11.1929.V.20151123.1429.006.html

